“错解题”的“分类归因”*

江苏省睢宁县第一中学 (221200) 贡苏丹 武瑞雪

当代科学家、哲学家波普尔说“错误中往往孕育着比正确更丰富的发现和创造因素.”“错解题”后，学生若能及时自行“悟”出各类“错因”，并及时“记录在案”，而教师又能根据作业或试卷批改中搜集到的学生错误，在课堂教学中进行必要的“分类归因”，定能充分挖掘“错解题”的教学价值，起到事半功倍之效.学生“错解题”的主要错因有：

1.不重视基础、书写不规范

案例1 (1)角α，β的终边关于y轴对称，若α=30°，则β=.

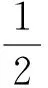
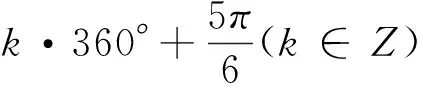
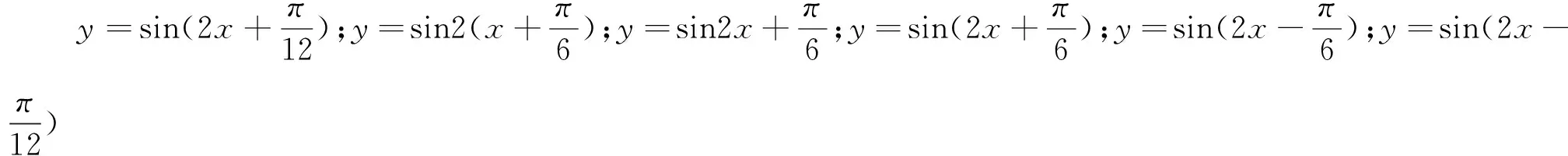
剖析：出现以上错解，主要是学生不重视基础知识，不重视课本，不重视书写的规范性.课本应是基础知识的源头，其中的例题具有典型性、示范性、资料性，只要在平时的学习中做到课前看，课后看，平时看，考前看，用心看，这样就一定能把基础打牢，做题时也一定会书写准确、规范.但是，调查及实践都表明，有些学生好高骛远，轻视课本，在基础知识还没记熟的情况下，就去盲目做题，结果常因书写不规范或用错公式而做错题，致使学习效率低下.

事实上，这两题的正确答案应为：

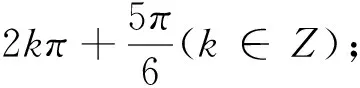
2.思维不严谨

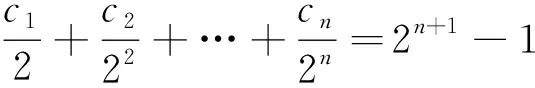
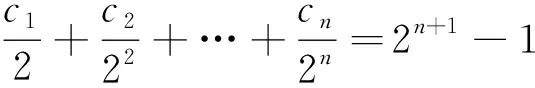
剖析:上述解题过程不够严密、严谨，导致虽懂基础知识，却做错了题.事实上，式子①n≥1，式子②中n≥2，故式子③和④中n≥2，因此，应验证n=1是否满足④式.

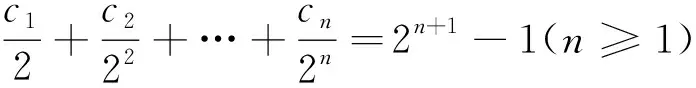
3.不擅于等价转化

调查发现，部分学生解题时，经常出现因某一步转化的不等价，造成前功尽弃，不得分或得分极低的情况.

案例3 设f(x)=x2-6x+1，问a取何值时，方程f(sinx)=a-5sinx在[0，2π)上有两解？

生众：设sinx=t，又x∈[0，2π)，所以t∈[-1，1]，因为方程f(sinx)=a-5sinx在[0，2π)上有两解，所以关于t的方程t2-6t+1=a-5t在[-1，1]上有两解，即关于t的方程t2-t+1=a在[-1，1]上有两解.

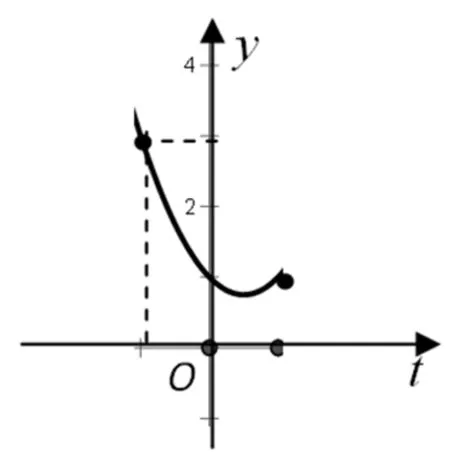
图1

剖析：调查到的考查结果显示部分学生给出上述错误解法，究其原因，主要是换元后进行了不等价转化.

图2

正解：设sinx=t，又x∈[0，2π)，如图2，得t∈[-1，1].

4.不擅于反思

解题后反思，利于总结经验、完善认识、提高能力、形成技能技巧，利于促进思维更加缜密、完善和优化，利于培养批判性思维品质，利于避免“题海战术”及“教师一讲就会，自己一做就不会或做错”的现象发生.

但是，调查显示，很多学生在解题中或解题后没有反思的自觉性，从来不主动反思解题时考虑是否有疏漏？是否出错？用到哪些基础知识、基本方法？为什么要这样做？不去反思是否有更简捷、更优美的解题方法？没有错题本，没有“逢错则记”的习惯，失去很多有用的“错误资源”，导致老错误重犯，学习效率低下.

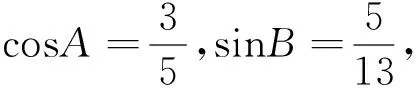
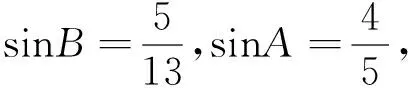
有了上述的反思过程，学生印象会深刻得多，如学生能及时记录，并经常翻看复习，则再遇此类问题时，定能有意识地规避错误，并顺利解之.养成阅读教材或教辅书上的例题解答之后及时反思的习惯，可有效避免“例题读得懂，题目一变就不会”的现象发生．

5.不擅于分类讨论

案例5 若cn=4n+(-1)n-1λ·2n+1(λ为非零整数，n∈N*)，试确定λ的值，使得对任意n∈N*，都有cn+1>cn成立.

正解：因为cn=4n+(-1)n-1λ·2n+1，所以要使cn+1>cn对任意n∈N*恒成立，即cn+1-cn=4n+1-4n+(-1)nλ·2n+2-(-1)n-1λ·2n+1>0对任意n∈N*恒成立，所以3×4n-3(-1)n-1λ·2n+1>0对任意n∈N*恒成立，即(-1)n-1λ<2n-1对任意n∈N*恒成立①.

(ⅰ)当n为奇数时，即λ<2n-1恒成立，当n=1时，2n-1有最小值1，所以λ<1.

(ⅱ)当n为偶数时，即λ>-2n-1恒成立，当n=2时，-2n-1有最大值-2，所以λ>-2.

综合(ⅰ)、(ⅱ)，得-2<λ<1，又λ为非零整数，则λ=-1，所以存在λ=-1，使得对任意的n∈N*，都有cn+1>cn.

点评:检测之后，进行试卷分析发现，部分学生因缺乏分类意识，做到步骤①时，不知如何继续下去；另有一部分学生在分类讨论之后，不会归纳总结，遗憾作罢；还有一部分学生，综合(ⅰ)、(ⅱ)，误得λ∈R.事实上，分类讨论后，最后的归纳总结常有以下三种情况：

(1)并集型：如“已知函数f(x)=(k2-1)x2+2(k-1)x+1的图象全在x轴的上方，求k的取值范围”，应按k2-1=0和k2-1≠0分类讨论，而两类的结果k=1和k>1，都符合题意，故最后结果应取各类中k取值集合的并集，得{k|k≥1}；

(2)交集型：如上述案例5，将n按奇数、偶数分类讨论，两类结果中λ取值的公共部分才是符合题意的，故取交集；

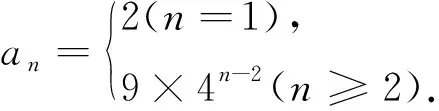
学生“错解题”的原因很多，限于篇幅不能穷尽.教学中，教师可以通过作业或试卷批改“分类”集中来自学生的“典型错误”，阶段性地开设“纠错课”，让学生自行纠错或相互纠错，培养学生批判性思维能力以及质疑的习惯，让学生意识到“反思透一道错题的错因”要比“解出一道正确的题目”更有价值.