多解型作业讲评的案例与反思*

福建省上杭一中 (364200) 张 露 陈玉生

多解型作业讲评对发展学生思维能力有直接效应，教师要正确处理好讲与评的关系，做到既“讲解”又“点评”,才能使数学知识的“联”与思维方式的“变”有机结合起来，有效提高不同层次的学生的变通能力，学会更加自然理性地思考，真正实现“授人以渔”.但不少教师对作业讲评教学的目的、价值等把握不准，忽视解题的优化功能，让一题多解教学偏离初心，是一个值得大家深思的问题.

一、案例展示

定义域为D的函数f(x)，若满足条件：①函数f(x)在D上是单调函数；②存在区间[a,b]⊆D，使得f(x)在[a,b]上的值域是[a,b]，则称函数f(x)为“成功函数”．

(1)判断函数f(x)=2x-1是否为“成功函数”？若是，求出满足条件的a与b的值；若不是，说明理由；

本题是高三一轮复习月检测题，第(1)题得分率高，第(2)题做得很不理想.在讲评教学中，笔者试着从学生错解入手，通过修正和优化，打通知识联系.

(一)展示错解，探究错因

可求得t>0.

教师：请同学们思考并讨论该解答错在哪里？

教师：能具体解释一下吗？

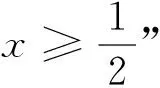
(二)矫正错误，获取正解

教师：说得好！同学们能否对其矫正呢？

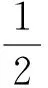
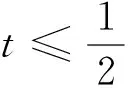
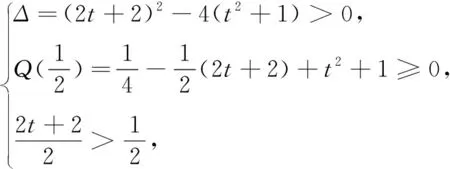
此不等式组无解.

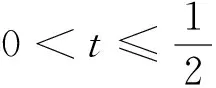
教师：该同学从方程的角度切入，利用了分类讨论的思想矫正了生1的错误，值得表扬！但求解过程比较繁，是否有可优化之处？

(三)联系变通，发现巧解

生3：可以避免分类讨论.

教师：两位同学对方程根的问题作了深入的分析，通过逐步优化，矫正错解，优化正解，充分展现了他们良好的数学功底.

(四)深挖本质，发掘简解

法3：方程(x-t)2=2x-1在x≥t时有两个不等的实数解，必须满足

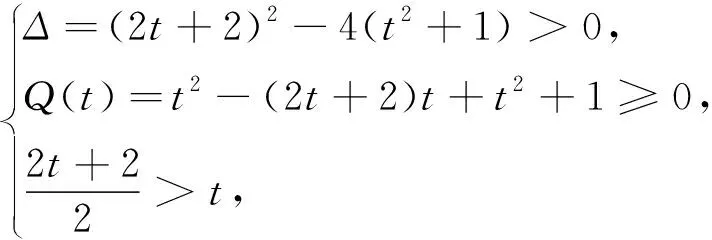
学生：此法太简捷了！

(五)多元表征，探寻多解

图1

教师：方程与函数是高中数学的重要知识，它们之间存在密切联系.能否从函数角度对此问题重新表述一下呢？

生5：老师，本题还能从形的角度观察求解.

图2

教师：以上从方程与函数的角度切入，利用数形结合思想，不但纠正了错解，还获得了正解、巧解、简解等多种不同解法.其中，法1利用了方程根的分布情况，它是解决此类问题的基本方法，法2虽然进行了优化，避免了分类讨论，但计算量仍然较大；法3充分挖掘了题目的隐含条件，是本题的创新解法；法4和法5充分体现了方程与函数之间的内在联系，法4最简捷，转化为学生熟悉的二次函数知识，是学生易接受的一种好方法.

二、教后反思

(一)注重通法、彰显联系是多解型作业讲评的关键点

多解各显精彩，联系更显“自然”.多解型作业讲评不能过分追求方法的数量、强化特殊的技巧，而应注重通性通法，并在各种解法之间呈现知识的联系，以及这些联系构建的过程，让学生习得结构化的数学知识.本案例在通法1的基础上，联系所学相关知识，拾级而上，逐步优化，让方法自然获得.只有实现以知识为载体的自然联系，方法才能水到渠成.注重通法、彰显联系才是好的数学解题教学.

(二)深挖本质、多元表征是多解型作业讲评的策略点

问题的表征能力直接影响解题.教师要引导学生追本溯源，深挖本质，多元表征，才能将问题灵活变通.法2的“巧”和法3的“简”只是表象，它的本质仍然是基于法1中方程根的分布情况，法5的求解也源于法4方程与函数的思想，让通解、巧解、简解之间实现了沟通！只有不断提高学生对问题的表征能力，才能让其用更高的观点，更广的视野，更理性的眼光去变通数学问题的思考方式，让数学解题绝处逢生、左右逢源.

(三)善待错误、变错为措是多解型作业讲评的突破点

学生错误是学生的原发思想，贴近学生的能力和思维，只不过是认识上产生的偏差.与教师给出的“奇思妙解”相比，它更能激发学生的问题意识和探究欲望，有效拓宽了多解的来源渠道.本案例中，教师没有急于抛出自己的思路将其强加给学生，而是从学生的典型错误出发，联系相关知识，逐步优化，变错为措，从而获得正解、巧解、优解、简解，充分挖掘了错误的潜在价值，让学生在“误中悟，思中醒”.关注学生所思所惑的解法更易被学生接受并迁移，更能有效提升学生的变通能力.

(四)优化思维、发展智能是多解型作业讲评的着力点

多解型作业讲评不能止于完成解题，要着力提升学生的思维能力，延伸解题思维的长度，避免“解法展览”现象.本案例在5种方法讲解后，教师能引导学生进行各种解法的对比与评价，让学生明白哪些是通性通法、哪些是最优解法、哪些是最合理解法、哪些解法本质是一样的．让学生在比较中深化认识、优化思维、固化优解，学会今后处理此类问题时灵活选择方法，真正快速地一题一解！而不至于走入一题多解的迷雾．

(五)培养思想、提升素养是多解型作业讲评的归宿点

数学思想方法影响思维的方式.要提升学生善于变通问题的思考能力，须关注解法是否反映出数学问题的本质，能否体现出不同数学思想方法的运用．本案例5种方法紧紧围绕方程与函数思想，数形结合思想展开，在多解探究中让学生洞察其背后的深刻与必然，感受使用思想方法解题的魅力，只有从问题中寻找解题的更高背景，从思想层面去引领，才能将学生的思维触角延伸到更深的层次、更广的方向.这对提升学生的数学素养，学科思维的发展大有好处，真正让学生终身受益.

多解型作业讲评要以学生的能力为基点，学生的发展为指向，学生的活动为依托，彰显解题的优化功能，才能联系更多知识，变通思维方式，迁移解题方法，让学生成为解题的智者.