汽车排气系统振动模态分析与悬挂位置优化

高 琦,庞 茂

(浙江科技学院 机械与能源工程学院,杭州 310023)

排气系统是汽车的重要组成部分,在很大程度上影响汽车的噪声与振动,因此其振动问题得到了广泛的关注。汽车排气系统一般通过法兰与发动机排气歧管相连,并通过吊耳与车身底板相连。排气系统受到发动机激励、路面激励等产生剧烈振动,通过吊耳传递至车身底板,进而严重影响整车的舒适性[1-3]。在过去,一般采用试验法来对汽车的排气系统振动问题进行分析,但这种方法耗时长、成本高,且主要依赖研究人员的主观经验。随着计算机技术的进步,有限元法等已成为排气系统振动研究的主要方法[4]。例如,文献[5]直接通过振型云图来判断排气系统的最佳悬挂点;文献[6-8]运用平均驱动自由度位移(average drive degree of freedom displacement,ADDOFD)法来进行排气系统悬挂位置的优化,获得了较好的结果,其中文献[7]利用层次分析法来获得各阶模态振型的权重因子,使结果更加准确,文献[8]将模型整个导入编写好的MATLAB处理程序中以获得模态位移云图,提高了工作效率;文献[9]通过对排气系统进行频响分析得到模态叠加云图来选择位移最小的点作为悬挂点;文献[10-11]分别利用综合模态节点法和振动传递函数法来选择排气系统的最优悬挂点;文献[12]通过对排气系统的灵敏度分析来优化悬挂位置,减小了在怠速状态下排气系统的振动。以上研究所使用的排气系统均采用两级消声器,而目前关于单级消声器的排气系统如何优化的研究尚不多见。因此,本研究建立某型号车辆排气系统(单级消声器)的有限元模型,运用Ansys软件对排气系统进行振动模态分析,并利用ADDOFD法来优化排气系统的悬挂位置,以改善整车的噪声与振动性能。

1 基本理论

1.1 模态分析

减小排气系统的振动必须确定其振动特性,这需要对它进行模态分析,即利用振型矩阵(每列为各阶振型)作为变换矩阵,将物理坐标转换为模态坐标,使一个线性时不变系统的振动微分方程组解耦,从而得到一组独立方程(该方程用模态坐标和模态参数描述),以求出该系统的模态参数[13]。

若一个线性定常系统具有n自由度,那么该系统的振动微分方程可以表示为

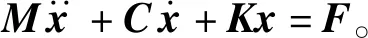
(1)

式(1)中:M为系统的质量矩阵;x为位移向量;C为系统的阻尼矩阵;K为系统的刚度矩阵;F为节点载荷向量。

汽车的排气系统结构较为复杂,传统的理论计算难以得到准确的结果,现在一般采用数值算法求解。本研究使用有限元法进行模态分析,把一个结构看成由若干通过结点相连的单元组成的整体,先进行单元分析,然后再把这些单元组合起来代表原来的结构(即数值模型)进行整体分析。

1.2 ADDOFD法

一个多自由度系统,若为单点激励,则该系统的响应点与激励点之间的频响函数[14]

(2)

式(2)中:n为响应点;p为激励点;r为模态阶数;φnr为点n第r阶模态振型系数;φpr为点p第r阶模态振型系数;Mr为模态质量;ωr为模态固有频率;ω为激励频率;j为虚数;ξr为模态阻尼比。

若激励力的频率ω=ωr,则式(2)可简化为

(3)

一个线性系统,其位移幅值和其频响函数的幅值成正比关系,即

(4)

将振型用质量矩阵进行归一化处理,并假设各阶模态的阻尼系数大致相等,则可以得到

(5)

根据式(5),可以得到第j个自由度的平均驱动自由度位移

(6)

通过ADDOFD法可以得到在一般激励条件下(指在一定频率范围内全部模态振型都被激发的情况)某一自由度的相对位移响应,再通过相对位移响应的数值大小来优化排气系统吊耳的悬挂位置。

2 有限元建模与模态分析

2.1 有限元模型的建立

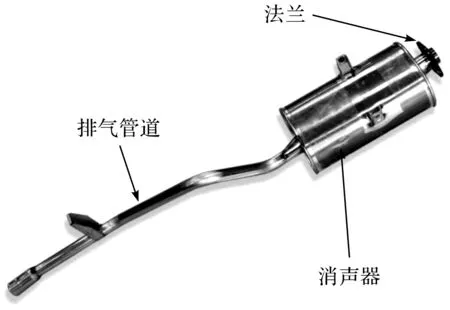
图1 排气系统的组成Fig.1 Composition of exhaust system

本研究所涉及车型的排气系统主要由排气管道、消声器和法兰3部分组成,如图1所示。要对排气系统进行振动模态分析,首先必须建立有限元模型。近年来国内外在排气系统的建模方法上形成了以梁单元为主和以壳单元为主的2种不同方法[15]。本研究使用Hypermesh软件来建立有限元模型,模型以壳单元为主,其中排气管道和消声器简化为壳单元,法兰简化为体单元。模型参数如下:法兰厚度为5 mm,消声器壁厚为1.5 mm,排气管道壁厚为1 mm,材料的弹性模量为210 000 MPa,泊松比为0.3,密度为7 900 kg/m3。排气系统有限元模型如图2所示。

图2 排气系统有限元模型Fig.2 Finite element model of exhaust system

2.2 振动模态分析

Ansys中提取模态的方法有Block Lanczos法、子空间法、Power Dynamics法、减缩法、不对称法和阻尼法。本研究选择Block Lanczos法对排气系统进行模态分析,该方法具有运算快、求解精度高、不易丢根等优点[16]。在使用Ansys软件进行模态分析后,利用杭州亿恒科技的模态测试系统对排气系统进行模态试验来验证有限元模型的合理性。试验模态分析指通过对实际系统的振动模态测试来获得其模态参数,有激振器激励法和力锤激励法2种,本研究使用力锤激励法。

根据排气系统的实际工况,在排气系统上布置47个测点,测点分布如图3所示。在进行模态试验前需将排气系统用绳子悬挂起来,以保证其处于自由状态,排气系统试验布置如图4所示。使用多点激励、单点响应法,将加速度传感器固定于测点33上(该点便于固定,且与前端和末端的距离适中,能够较为准确地接收信号),使用力锤对其余测点逐一进行试验,力锤输出的激励信号经电荷放大器放大后与加速度传感器输出的响应信号一同输入数据采集与分析仪,再输入计算机,经过数据分析软件Test EngineX与模态分析软件Modal Genius处理后得到模态数据。排气系统模态试验流程如图5所示。

图3 测点分布Fig.3 Distribution of test points

图4 排气系统试验布置Fig.4 Arrangement of exhaust system test

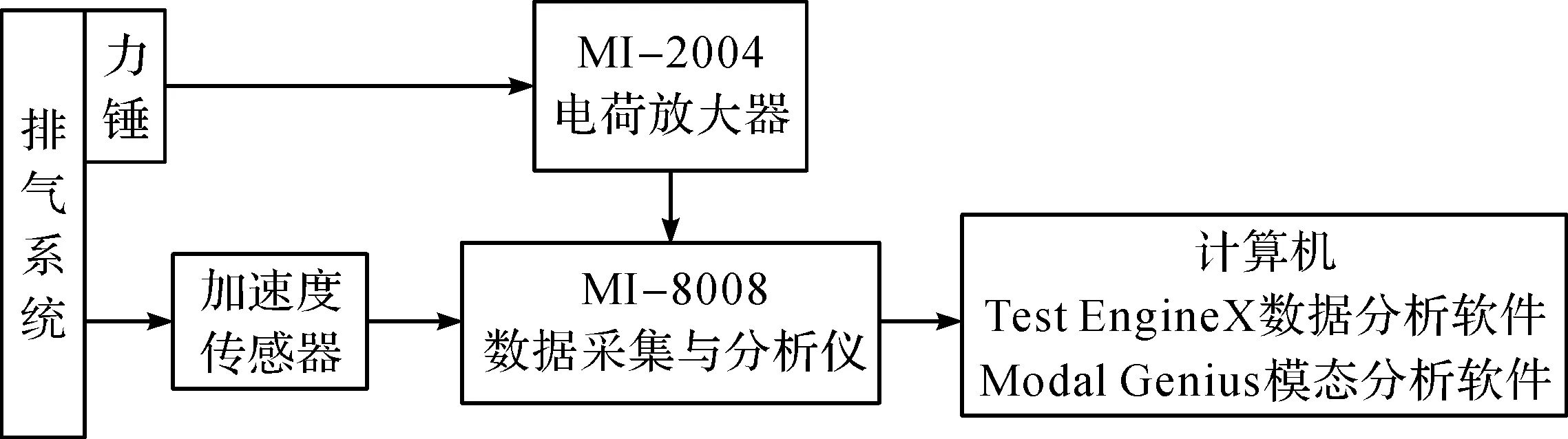
图5 排气系统模态试验流程Fig.5 Modal test procedure of exhaust system

300 Hz内的Ansys模态分析与力锤激励试验获得的排气系统各阶模态频率见表1,两者之间的误差最大为8.9%,小于10%，这说明排气系统的有限元模型是合理的。图6是排气系统3种典型的模态振型:图6(a)为1阶模态振型,其振型主要为排气管前段的纵向弯曲;图6(b)为3阶模态振型,其振型除了排气管的弯曲外,消声器部分也开始发生弯曲;图6(c)为6阶模态振型,其振型除了排气管和消声器的弯曲外,排气管部分还发生了扭曲。

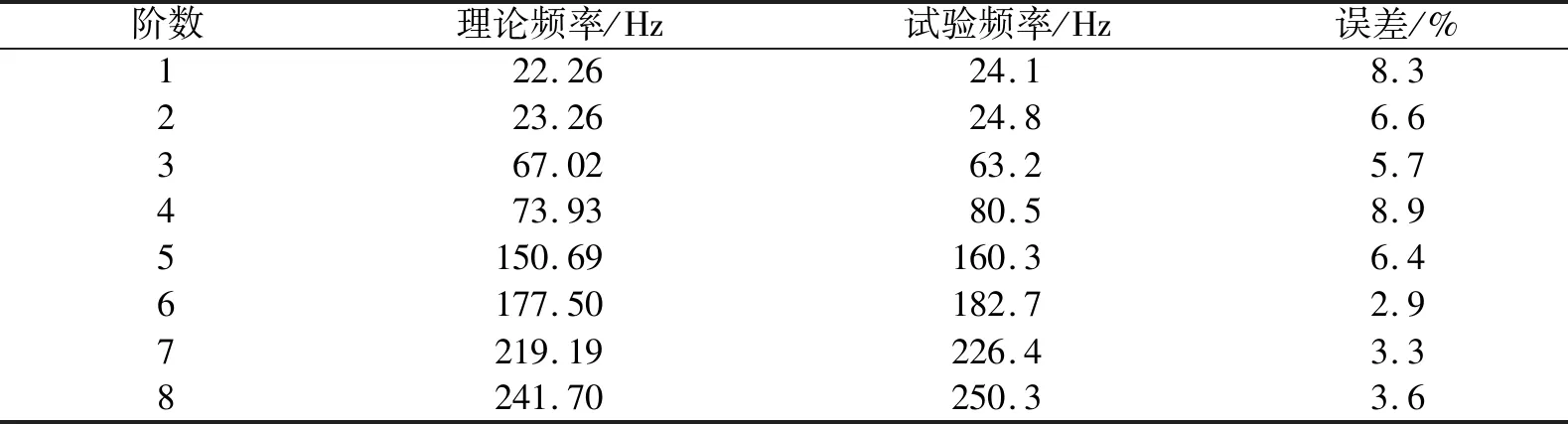
表1 排气系统的各阶模态频率(300 Hz内)Table 1 Modal frequencies of exhaust system(within 300 Hz)

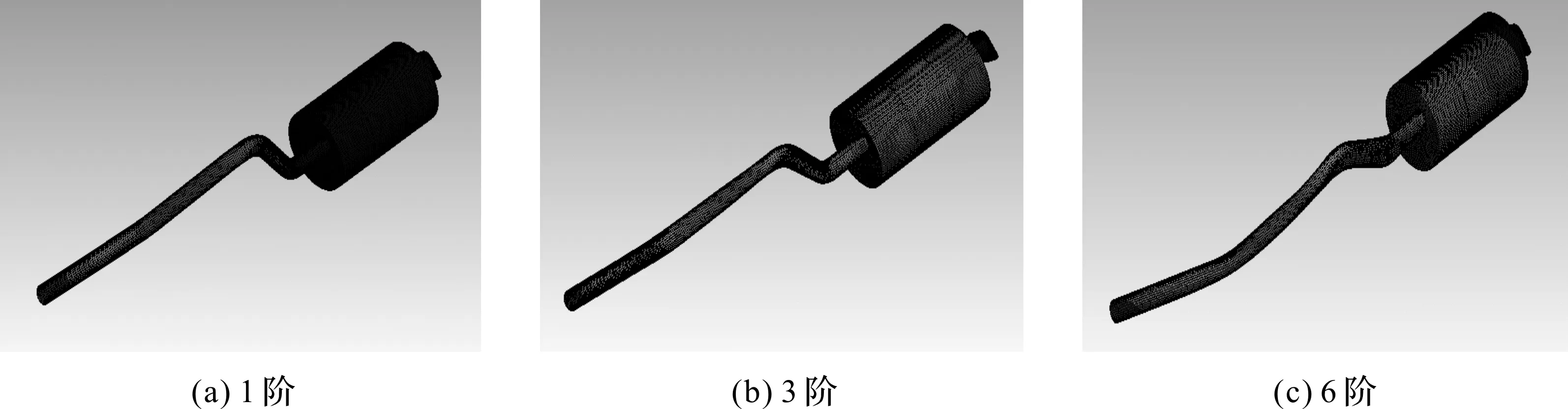
图6 排气系统的模态振型Fig.6 Modal mode of exhaust system

通过模态分析,我们可以了解到排气系统在一定频率内(300 Hz内)的模态数,以及其各阶模态频率和相对应的振型与阻尼;排气系统的模态频率应当与发动机(特别是怠速工况下的)的激励频率错开。这一振动模态分析为排气系统的结构优化和悬挂位置的优化提供了参考,同时也为车辆平顺性的匹配提供了一定的依据。

3 悬挂位置优化

悬挂位置优化是从振动传递方面来降低排气系统振动和噪声的方法。在过去,选择最佳悬挂位置主要是依靠研究人员的经验来进行选择,这种方法主观且随机[17]。本研究采用ADDOFD法,利用2.2节获得的模态分析数据来优化排气系统的悬挂位置。

根据有限元模型,在排气系统上选择85个预选悬挂点,使用ADDOFD法获得了排气系统各预选悬挂点的平均驱动自由度位移,如图7所示。由图7可知,曲线上存在3个极小值点A、B、C,这些点意味着在排气系统上相应部位的振动幅度较小,因此其传到车身底板的振动最小。这些极小值点可作为排气系统悬挂位置的最佳点。排气系统悬挂点的优化结果如图8所示。

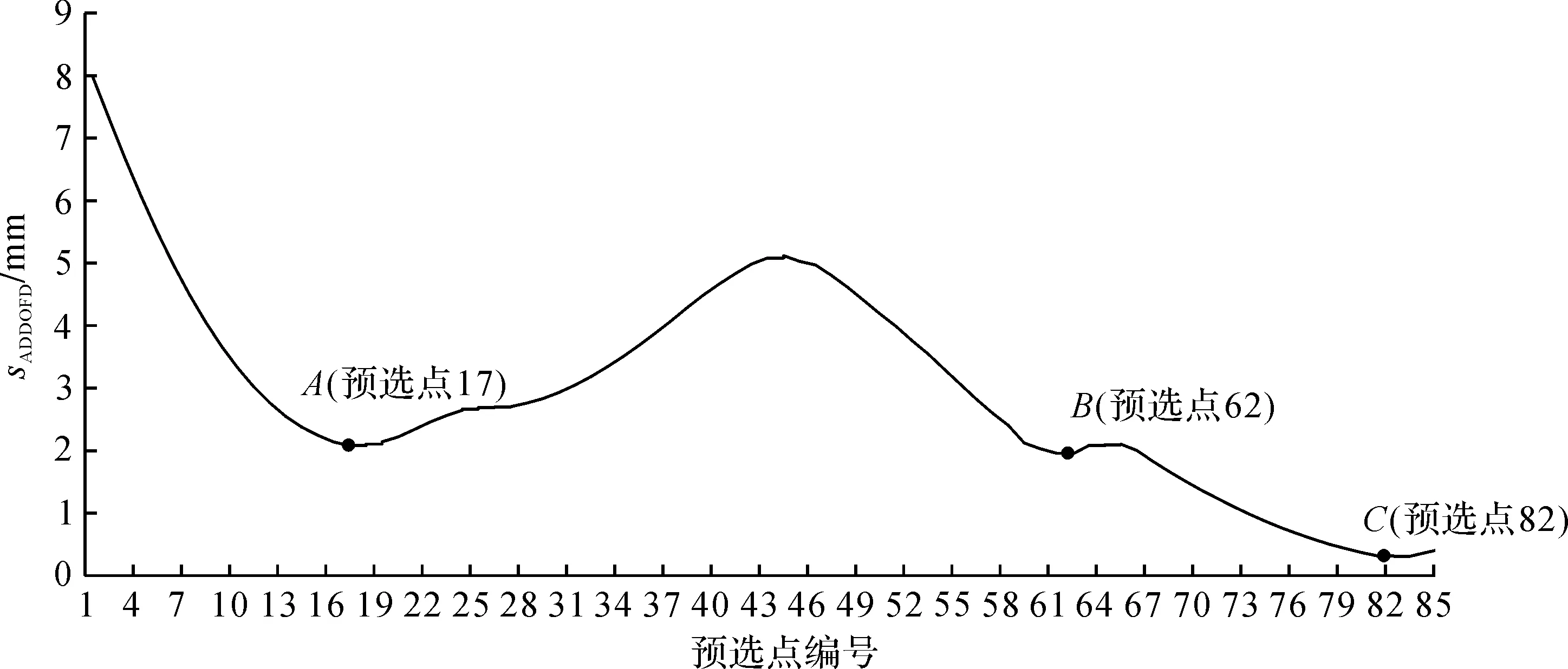
图7 排气系统各预选点的平均驱动自由度位移Fig.7 ADDOFD of each preselected point of exhaust system

图8 排气系统悬挂点的优化结果Fig.8 Optimization results of suspension points of exhaust system

4 结 语

本研究利用Hypermesh软件建立了排气系统的有限元模型,并使用Ansys软件对其进行了模态分析,得到了各阶模态频率,进而同模态试验所得到的数据进行比较,验证了排气系统有限元模型的合理性。在此基础上,利用ADDOFD法获得了排气系统部分节点的加权位移曲线,结果表明,曲线的极小值位置作为排气系统悬挂点的位置可以减小排气系统传到车身底板的振动,从而改善了整车的噪声与振动性能,验证了ADDOFD法可用于单消声器排气系统的悬挂位置优化。