基于信号强度的最大似然振幅估计迭代算法

金 艳,孟 婷,支石伟,吴茗蔚,周武杰

(浙江科技学院 信息与电子工程学院,杭州 310023)

从一系列信号样本中估计出信号的振幅、频率、相位等未知参数是通信系统中的重要研究内容。目前通信系统中要获得信号的振幅参数,需经过一系列复杂的计算,当且仅当信号的频率参数恢复后,才能得到信号的振幅参数估计[1-2]。不仅如此,频率估计过程复杂、计算困难[3],易出现异常值[4-5]等,其准确度极大地限制了振幅估计的性能。振幅参数的估计性能总是依赖于频率参数估计的性能[6],这对开关键控调制等仅需要振幅参数估计的通信系统而言是需要避免的。因此有必要研究出不受限于频率估计的振幅估计算法。

1954年,Slepian[7]提出了信号的参数估计问题,将费雪与克拉美罗理论应用于经过加性高斯白噪声信道的信号参数估计中,但他的大部分工作都集中在连续时间观测模型上。随后Rife[8]提出了基于离散时间序列,经过加性高斯白噪声信道的信号参数估计方法。然而,其实际算法非常复杂,需要找出基于快速傅里叶变换的频域解。Sijbers[9]357提出了莱斯分布参数估计的最大似然算法,但并未给出振幅估计子模型。本文假设对信号的振幅、频率、相位参数没有任何先验知识,即振幅可能是任意的非负值,频率和相位可能是区间[-π,π)之间的任意取值,则最合适的参数估计方法是最大似然估计[4]。一般通过利用接收信号的幅度和相位,样本均值估计子可实现克拉美-罗下界[10]。然而,只有接收信号的幅值时,样本均值估计子并非最优。矩量法是一种常用的估计方法,因为n次方样本均值是n阶矩的无偏估计[11],所以用n次方样本均值即可逼近莱斯分布的n阶矩。例如,传统的均方根振幅估计子是利用二次样本均值逼近二阶矩,但其性能还有待优化。

本文研究基于信号强度的振幅估计问题,该问题等价于经典的莱斯分布参数估计[12]问题。本研究结果不仅能够应用于通信领域,如通信信号强度测距[13]、信道建模[14-15]等,还能够应用于磁共振成像[16-18]、语音处理[19]、雷达[20]等领域。

1 信号模型

通信系统的接收信号是一种可用复数表示且包含复加性高斯白噪声的信号r(k),信号模型[21]为

r(k)=Aej(ω k+θ)+n(k),k=0,1,2,…。

(1)

式(1)中:r(k)为接收信号;A为发送信号的实际振幅,可以是任意非负实数;ω与θ分别为信号的频率与相位;n(k)为一种圆对称、独立同分布的复加性高斯白噪声,其均值为零,方差为2σ2。

接收信号的几何相量表示方法如图1所示。n(k)被分解为平行于Aej(ω k+θ)的同相分量nI(k)和垂直于Aej(ω k+θ)的正交分量nQ(k)。

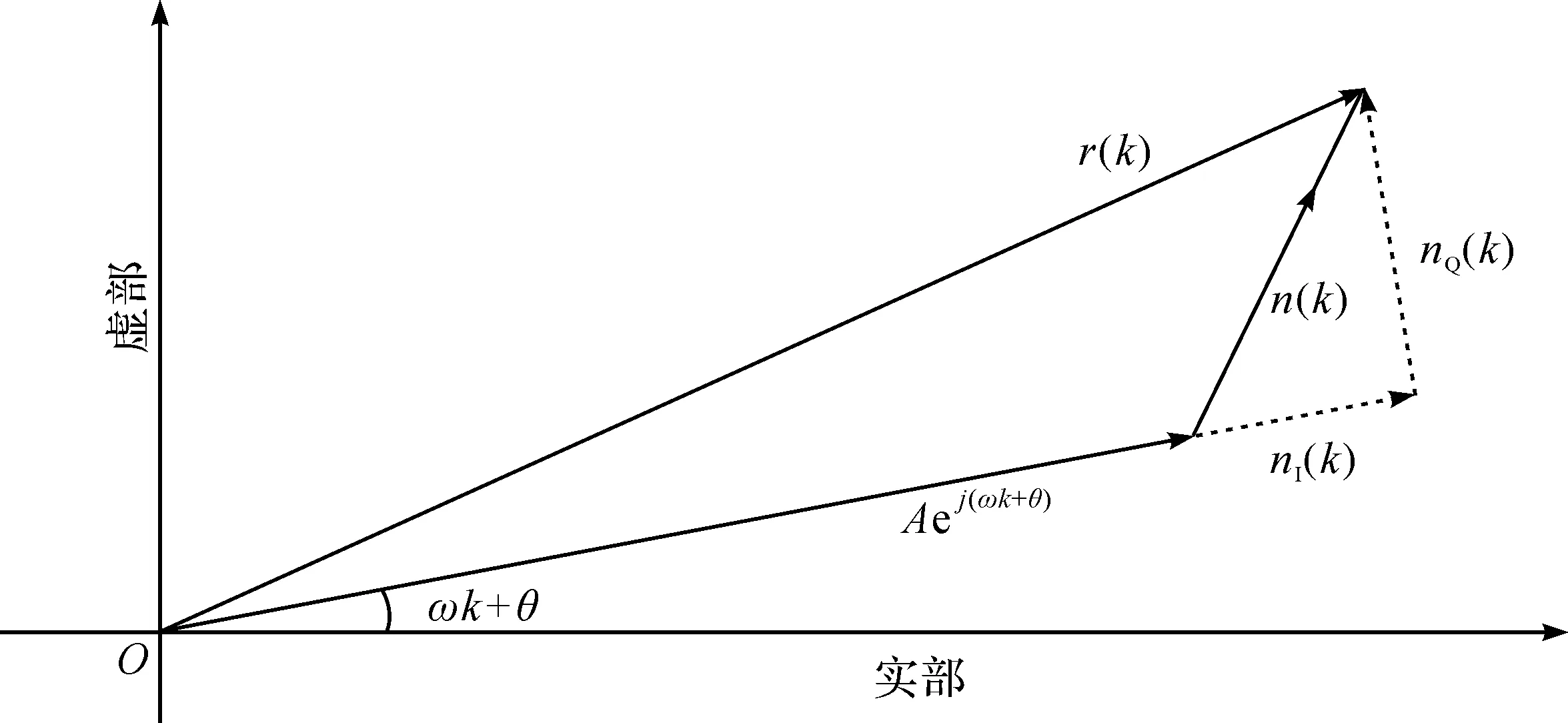
图1 接收信号的几何表示Fig.1 Geometric representation of received signal

由于n(k)是圆对称的,且nI(k)和nQ(k)两个正交分量在统计学上是独立同分布的高斯随机变量,所以从图1可以看出新建立的坐标系即为原坐标系逆时针旋转角度ωk+θ,故信号模型为

r(k)=A+nI(k)+jnQ(k)。

(2)

该模型也适用于恒定传输信号的情况。在新建立的坐标系中,r(k)模值为

(3)

2 传统振幅估计算法

2.1 样本均值估计

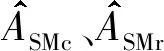
(4)

当可以得到r(k)的复数值即通过相干检测得到的r(k)时,估计子

(5)

式(5)中:N为数据样本数量。此估计子的克拉美-罗下界(Cramér-Rao lower bound,CRLB)为2σ2/N。

当可以采集到复数r(k)的实部为样本时,即消除了虚部,使噪声功率降低了一半,估计子

(6)

当只能检测信号r(k)的幅度值即信号强度时,估计子

(7)

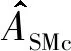
2.2 均方根估计

数量为N的样本均方值为

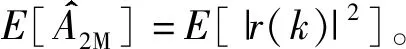
因此可得到传统的均方根振幅估计子

(8)

3 最大似然估计的迭代算法

3.1 最大似然估计

信号强度|r(k)|是服从莱斯分布的随机变量,其条件概率密度函数[9]357

(9)

式(9)中:I0(·)为零阶第一类修正贝塞尔函数。由p(|r(k)||A,σ2)可知接收信号模值的联合条件概率密度函数

(10)

式(10)中:N为信号强度样本数量。式(10)的似然函数

假设接收机的噪声方差σ2已知,或已通过某种噪声方差估计方法估计得到相对准确的σ2,就能够凭借最大似然原理估计振幅A。将似然函数Λ(A,σ2)取对数求偏导,得到取极大值条件下的对数似然方程,即需要满足

(11)

(12)

式(12)中:I1(·)为一阶第一类修正贝塞尔函数。式(12)即为利用最大似然估计得到的振幅估计隐函数,该隐式解即为基于信号强度恢复信号的振幅信息。由于无法直接解得其值,因此需运用迭代算法求解。

3.2 迭代算法

3.2.1 阶梯迭代法

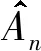
(13)

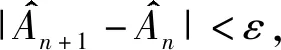
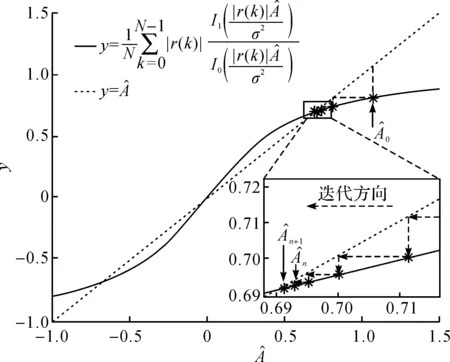
图2 阶梯迭代算法原理Fig.2 Schematic diagram of iterative step algorithm

3.2.2 牛顿迭代法

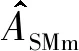
(14)

式(14)中:

(15)

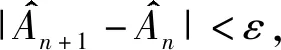
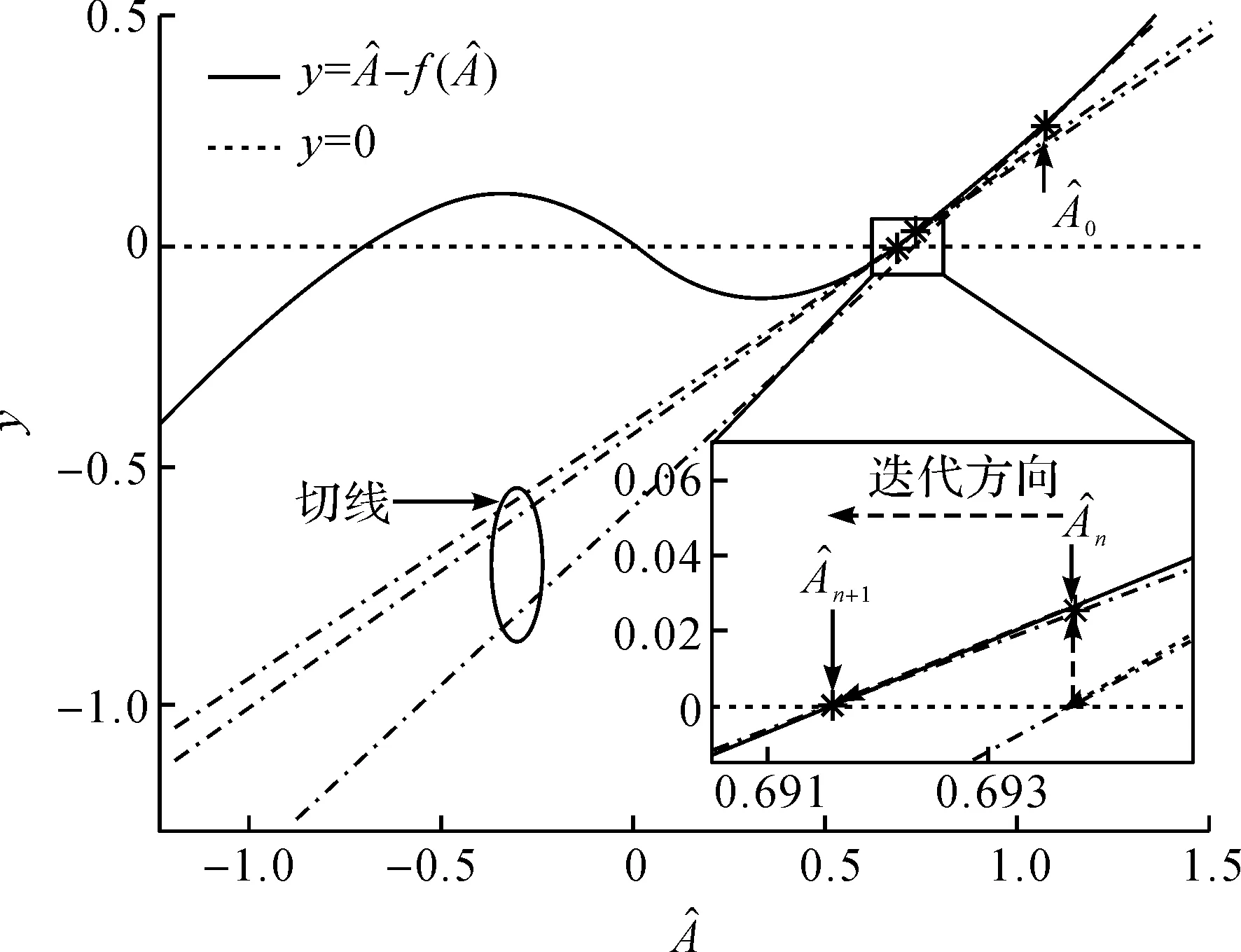
图3 牛顿迭代算法原理Fig.3 Schematic diagram of iterative Newton’s algorithm

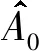
4 性能仿真分析

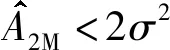
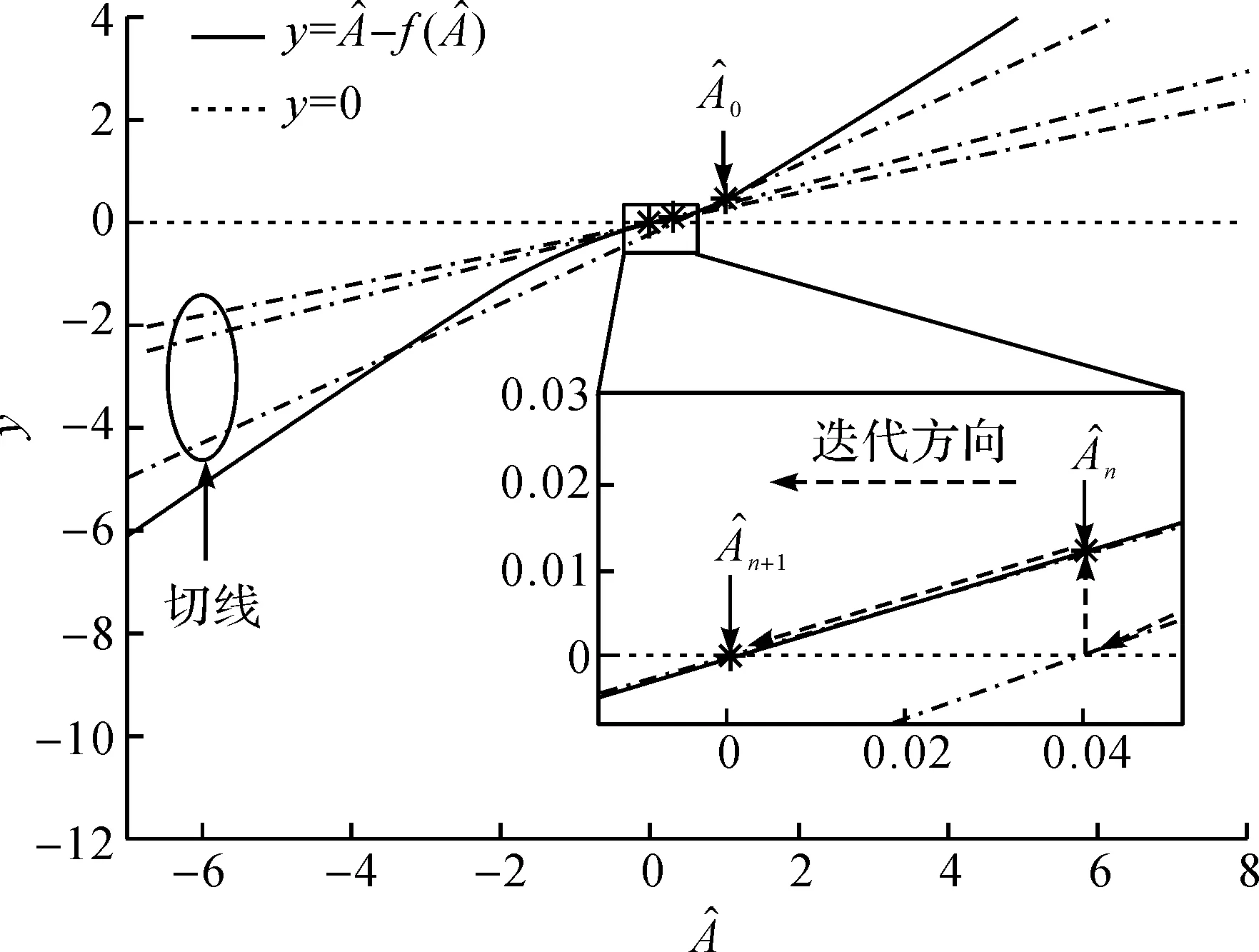
图4 γ=0 dB,N=10时仅含唯一解的牛顿迭代算法原理Fig.4 Schematic diagram of with known σ2 using the iterative Newton’s algorithm with only one solution with γ=0 dB and N=10

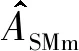
平均迭代次数的比较如图6所示,牛顿迭代算法的迭代速度远远高于阶梯迭代法。然而,对于每次迭代,牛顿迭代算法的计算复杂度较高,如表1所示,其中,NiS和NiNt分别为阶梯迭代算法与牛顿迭代算法的迭代次数。

图5 传统估计与迭代估计均方误差性能比较Fig.5 MSE comparison of conventional estimators and iterative estimators

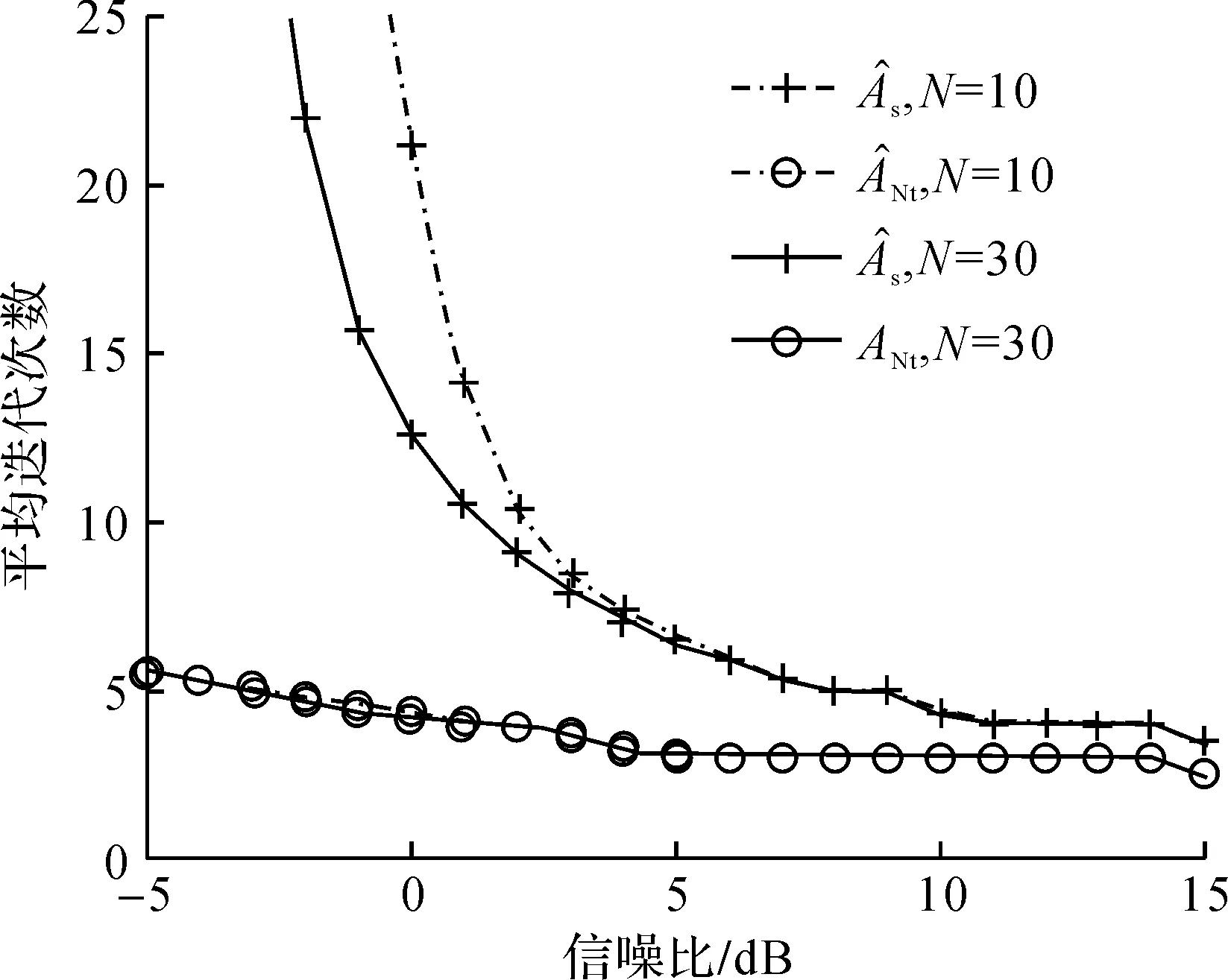
图6 阶梯迭代估计与牛顿迭代估计平均迭代次数比较Fig.6 Comparison of average numbers of iterations for iterative step algorithm and iterative Newton’s algorithm

表1计算复杂性比较
Table1Comparison of computational complexities

估计子乘法数量加法数量I1(x)/I0(x)ASMm1N-10ARMSN+2N0AS(3N+3)NiS(2N-2)NiS2N·NiSANt(9N+4)NiNt3N·NiNt2N·NiNt

5 结 语

本文研究了在无需频率和相位估计的情况下,仅利用接收信号的幅值估计发送信号的实际幅值问题,以及基于已知噪声方差情况下,最大似然幅度估计的两种迭代解法。结果表明,两种迭代算法具有相同的均方误差性能,均优于传统估计算法。本文所分析的问题是典型的莱斯分布参数估计问题的一个典型例子,研究结果可在生物工程、语音处理、雷达、测距、信道建模等领域应用。