基于多元逐步回归的RoboCup边界球研究

余培

（安徽工业大学计算机学院，安徽马鞍山243000）

RoboCup（即机器人世界杯）是一项在世界机器人竞赛领域中具有重大影响的专业竞赛，该比赛的设想首先是由加拿大教授Alan Mackworth 在论文［1]中提出的。1993 年6 月，日本研究人员Mi⁃noru Asada 和Hiroaki Kitano 决定启动RoboCup J锦标赛，后来扩展为国际项目，正式更名为机器人世界杯，简称RoboCup，因其融合多门学科的研究成果，现已成为当今科研的热点问题［2]。RoboCup仿真2D组是RoboCup下的一个分支项目，主要考察人工智能和团队策略的应用。

近年来很多学者将数据挖掘与建模的思想引入对RoboCup 比赛日志文件的研究中，均取得了很多成就，但对于边界球这一分支的研究较少。本文基于数据挖掘的思想，对日志文件中的边界球信息进行挖掘分析，为球队的决策改良做出理论指导。本文将球场划分为四个区域，解析日志文件，将比分差作为因变量，将四个区域内两支队伍边界球数目的差值分别作为四个不同的自变量，使用逐步回归的方式剔除不显著的两个自变量，并得出剩下两个显著的自变量与因变量之间的多元线性回归模型，由此得出能够对球队决策进行理论指导的结论。

1 问题的提出

RoboCup的日志文件通常被用来回放比赛内容，也可被当作数据源挖掘具有潜在价值的信息。基于比赛日志文件的挖掘分析，前人曾做过有关传球、球员跑位、球员阵型等方面的研究，例如学者陈梅利用密度峰值聚类算法对球队阵型进行研究［3]；学者田杰挖掘出比赛日志文件中的传球信息，采用偏最小二乘法探究对胜负影响最大的传球类型［4]；学者聂亮通过挖掘日志文件探索更高效的进攻跑位策略［5]。

边界球在足球比赛中十分常见，比赛中一旦足球被踢出界，将由对方球员在出界点将球掷回场内。基于日志文件挖掘的边界球技术研究是前人研究中关注度较低的一个分支，这方面的研究成果几乎是空白。比赛中与边界球相关联的因素有很多，例如对方的传球失误、铲球压力等，本文选取边界球分布和比分之间的关系作为研究对象。

2 研究方法

本文主要使用逐步回归的方法搭建多元线性回归模型，配合使用相关系数、拟合优度检验、F检验和t检验等方法。

2.1 多元线性回归模型

一般使用回归分析研究某一个随机变量与一个或几个变量之间的数量关系，所得到的回归方程依据所含的变量的数目不同，可被分为一元回归方程和多元回归方程［6]。在很多实际情况下，一种现象常常和多种因素连接在一起，即因变量的确定在很多情况下都是和多个自变量密切相关的。多元回归模型的应用场景十分广泛，例如学者付凤玲利用多元回归模型通过玉米苗期各项指标的耐旱系数预测其耐自交系的耐旱性［7]；学者林高用使用多元回归分析方法探究各金属的含量与合金耐腐蚀性的关系［8]。

设随机变量y与一般变量之间满足以下线性关系：是p+1 个未知参数，0β被称为回归常数

式（1）中被称为回归系数。y即因变量又称为被解释变量是p个自变量，被称为解释变量，ε是随机误差。大多数情况下采用普通最小二乘法计算多元线性回归方程的未知数

2.2 皮尔逊（Pearson）相关系数

通常使用皮尔逊（Pearson）相关系数来衡量两个连续变量之间的线性相关程度，用r来表示，它的计算公式为：

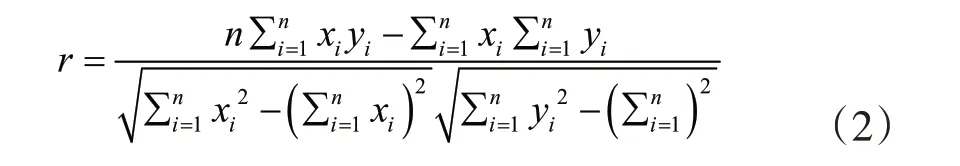
式（2）中的n代表样本容量，和分别代表自变量和因变量的均值。相关系数r的取值范围为1≤r≤1 ，其中r＞0 代表所研究的两个连续变量存在正的线性相关关系，r＜0 代表这两个变量存在负的线性相关关系；|r|≤ 0.3 表示两个变量几乎不存在线性相关，0.3 ＜|r| ≤0.5 表示两个变量具有中等程度的线性相关［9]，0.5 ＜|r|≤ 0.8 表示显著线性相关，而|r|> 0.8 则代表最为理想的高度线性关系。

2.3 多元线性回归模型的检验

多元线性回归模型的检验方式主要有拟合优度检验、F检验和t检验，各种不同的检验方式有其各自的优劣之处。

2.3.1 拟合优度检验

一般使用拟合优度R2来检验多元线性回归方程的拟合程度，其公式为：为回归平方和

其中为原始数据yi的总变异平方和。2R的取值在［0,1]之间，越接近1表示拟合的效果越好，但若2R过高需警惕过拟合现象。

2.3.2 多元线性回归模型的F检验

在多元回归分析中，通常使用F检验来检验所有的解释变量从整体上对因变量是否有明显的影响，建立F检验统计量如下：式（4）中的指残差平方和。当认为在显著水平α下，y和有显著的线性关系，反之认为它们之间没有显著的线性关系。多元回归分析的F检验反映模型整体的显著性，而无法检验单个自变量的显著性。

2.3.3 多元线性回归模型的t检验

与F检验不同，t检验可反映单个自变量和因变量之间的显著性，有时候会存在以下情况，即多元线性回归模型符合F检验，但其中的某些自变量无法通过t检验，这就说明当前所得到的模型并不是最优的，需要进行变量的筛选。

对于一个实际求解多元线性回归模型的问题，获得了n组观测数据(则线性回归模型可表示为：

将式（5）转换成矩阵形式为：y=X β+ε，其中

由此构造的t检验统计量如下：

ie为iy的残差为多元线性回归模型中的xj系数。确定显著水平α，若认为该自变量显著，否则认为该自变量不显著。

3 实验与结果分析

3.1 数据建模

首先将球场划分为若干区域使得边界球的横坐标离散化，再通过解析日志文件提取出左右两支队伍在各区域的边界球数目之差和比分差，由此构造解释变量与被解释变量。

3.1.1 球场的划分

仿真2D 的球场总长度105 m，总宽度68 m。边界球的纵坐标是固定值，横坐标是连续型变量，为了将其离散化，将球场划分为不同区域。划分球场的依据有均匀划分和基于信息熵划分等方式，这里为了简化模型，采用均匀划分的方式。依照习惯可将球场划分为四个区域、六个区域或八个区域，在后续实验中由于划分为六个区域或八个区域会使得各个解释变量的显著性太差，最终选择将球场划分为四个区域。如图1所示将球场平均划分为四个区域，区域名分别是和x4，被划分的球场区域以及其每个区域的横坐标范围如表1所示：

图1 球场区域划分

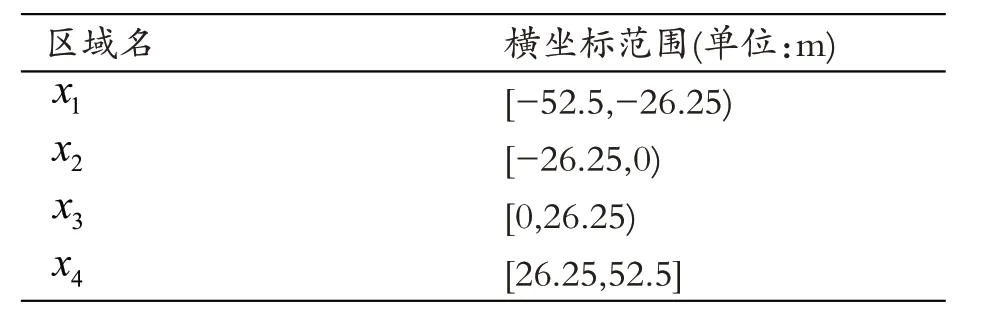
表1 球场区域划分范围

3.1.2 日志文件的解析

RoboCup的日志文件由比赛中的系统自动生成，分为rcg文件和rcl文件。rcg文件由当前周期、球的信息和球员信息等部分组成；其中球的信息显示了在当前周期球的横纵坐标以及沿x轴和y轴的速度；球员信息包含了球员标识以及各种参数信息。rcl 文件则包含具体的裁判命令信息。

在比赛状态发生改变的时候，rcg文件内会由单独成行的playmode后面的内容提示当前比赛的新状态，通常有play_on，corner_kick，foul_charge，goal，kick_in 等 等。其 中kick_in 代 表 边 界 球，kick_in_l 代表右方球员踢球出界，由左方球员取得球权在边界发球。反之kick_in_r则代表右方球员在边界发球。

本文选取安徽工业大学的YuShan 和其他三支不同队伍总共80 场比赛的日志文件作为数据源，为获取比赛双方在不同区域的边界球数目，使用Python语言解析rcg文件，提取比赛双方在四个区域的边界球数以及比分。例如解析某一场比赛，其结果如表2所示：

表2 某场比赛的解析结果

3.1.3 变量的构造

为了研究边界球分布与比赛得分的关系，将每场比赛双方队伍在各区域的边界球数与比分作差。将结果写入xls 文件中，得到的部分xls 文件如表3所示：

表3 部分xls文件

表3 中的第一列id 表示比赛的编号，从1 开始；第二到第五列分别为双方球队在各个区域的边界球数之差值，分别用解释变量x1,x2,x3和x4表示；第六列为左右队的分差，为因变量y。

3.2 多元线性回归模型的建立

利用Python计算出四个解释变量与因变量之间的皮尔逊（Pearson）相关系数矩阵，结果如表4所示：

表4 解释变量和因变量的相关系数矩阵

从表4 中可以看出，存在和因变量之间的相关系数非常低的自变量，例如 3x和y之间的相关系数仅有0.048 532，即并非所有的自变量都对y有很显著的影响，这就需要筛选出符合条件的自变量。

多元回归模型自变量筛选的方法有前进法、后退法和逐步回归法，文献［10]提出现阶段最受推崇的变量筛选方法是逐步回归法。与之相比，前进法无法反映引进新自变量后的当前自变量的显著情况，即有可能引入新的自变量后原本显著的某一自变量变得不显著，但是没有机会将其剔除；后退法则存在开始计算量太大等问题。逐步回归法吸收了前进法和后退法的优点，克服了它们的不足。具体方法是在引入一个新的变量后重新对模型进行F检验和t检验，剔除掉其中不显著的变量，直到没有显著的自变量被引入和不显著的自变量被剔除为止，故逐步回归法最后一步得到的模型是最优模型。

引入与y的相关系数绝对值最高的2x作为多元线性回归模型的第一个自变量，使用最小二乘法计算出的回归模型一以及各项参数如表5所示，并选取拟合优度R2和F检验对该模型进行检验。

表5 模型一及各项检验参数

该表的第二列表示该模型各变量的系数及该模型的常量，第三列表示t检验统计量的绝对值第四、第五列分别表示该模型的拟合优度R2和F检验的统计量。其中F值为1 1.500 >F0.01(1,78) ≈ 6.85，在α= 0.01的显著水平下显著，但R2很低。接下来在x2的基础上引入相关系数次高的x1，计算出的回归模型二以及各项参数如表6所示：

表6 模型二及各项检验参数

模型二计算出的F值为11.186，大于F0.01(2,77) ≈ 4.79，故在α=0.01 的显著水平下模型二显著；x1,x2的t值分别为3.099 和3.317，均大于t0.005(77) ≈ 2.617，可以得出在α=0.01 的显著水平下，x1,x2依然显著，故不需要剔除任何一个变量。

下面考虑x3,4x变量，依次引入它们，重新计算回归模型三和模型四，它们的系数、常量与各项参数分别如表7和表8所示：

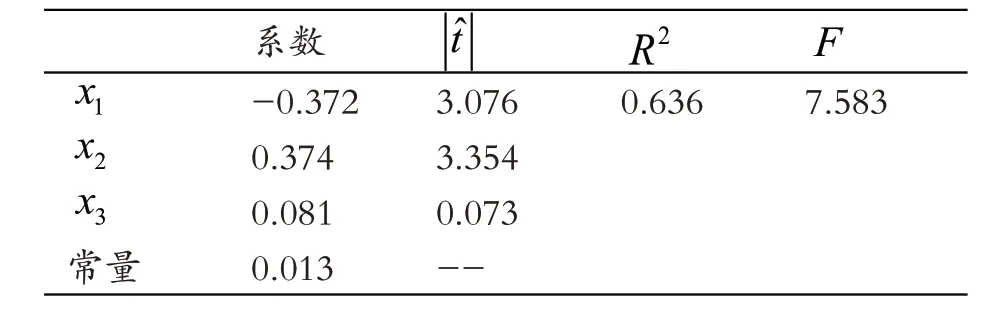
表7 模型三及各项检验参数

表8 模型四及各项检验参数

从表7和表8可以看出：模型三和模型四的F值均大于F0.01(3,76) ≈ 3.95，故模型三和模型四均显著，但是两个模型中x3和x4的均小于故x3,x4在模型三和模型四中均不显著，应被剔除，最终所得到的结果是模型二。

综上所述，模型二为最优的多元线性回归模型，其表达式为：

3.3 结果分析

式（7）为通过逐步回归法得到的边界球坐标和比分差之间最优的多元线性回归模型。令y> 0，得出下式：

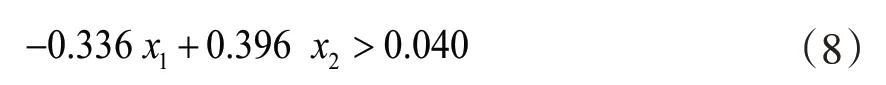
式（8）即为球队获得胜利的边界球分布模型，由前文中对该模型F检验的结果可得，在α=0.01 的显著水平下可以基本认为，边界球分布特征符合该模型的球队拥有较高的胜率。

通过各解释变量的系数可以看出，站在左队的视角，队伍落在［-52.5,-26.25)区域内的边界球数目越少或落在［-26.25，0)区域内的边界球数目越多，获胜的可能性越大。联系实际比赛，是由于对方球队在［-52.5,-26.25)区域的攻击普遍较强，导致我方的边界球易被对方截取甚至进球；而对方球队在［-26.25，0)区域的防守较弱，易被我方边界球突破得分。比赛中铲球和边界球密切相连，是造成边界球的主要原因，故一支队伍的边界球很大程度依赖于对方的铲球，这启示我们在比赛中应加强［-52.5,-26.25)区域的界外铲球，提高防守能力；并加强［-26.25，0)区域以得分为目的的进攻，使得x2区域的铲球尽可能多地铲向 3x区域，避免出界，以此达到在不同区域增加或减少对方边界球数的目的，从而影响边界球数目的差值，提高比赛的胜率。

4 结语

本文使用多元线性回归模型，以数据挖掘为主要思想，探究边界球分布和比分之间的数学关系。该回归模型对于实际比赛的启示是，站在左队的视角，在球场［-52.5,-26.25)区域内的铲球应该尽可能地出界，而在［-26.25，0)区域内的铲球应该铲向球场右半场。下一步工作是在球队的代码中运用该结论，有意识地控制不同区域铲球的方向和位置，以控制边界球的数目差，从而达到提升队伍胜率的目的。