流体黏性对受迫振荡水平圆柱受力的影响

袁剑平，毛鸿飞，赫岩莉，潘新祥，贾宝柱

流体黏性对受迫振荡水平圆柱受力的影响

袁剑平1，毛鸿飞1，赫岩莉1，潘新祥2，贾宝柱2

（1. 广东海洋大学海洋工程学院，广东 湛江 524088；2. 广东海洋大学海运学院，广东 湛江 524088）

【目的】准确预测显著黏性效应下结构物所受流体作用力。【方法】采用有限体积（FVM）方法构建两相流数值波浪水槽模型。首先，通过半潜水平圆柱受波浪力数值结果与前人实验数据的对比，验证数值模型的准确性。其次，对不同流体黏性下，受迫振荡淹没水平圆柱上的流体作用力进行数值计算，通过黏性流结果和势流结果的对比，分析流体黏性对圆柱受力的影响特征。最后，通过将黏性流和势流理论压力结果对比，并结合对圆柱周围黏性涡量场分布特征分析，解释不同流体黏性下，黏性流与势流结果之间出现差异的原因。【结果】在不同流体黏性条件下，圆柱所受各倍频流体作用力均出现一定程度上的差别，表明流体黏性的影响明显。【结论】相比势流理论，采用黏性流理论对受迫振荡水平圆柱受力的影响的研究更为准确。

圆柱；受迫振荡；流体作用力；数值模拟；波浪水槽

在流体与结构相互作用的流体动力学领域研究中，近自由面淹没水平圆柱在水中受迫振荡问题受到了关注和研究。基于势流理论展开的相关研究为了简化计算，将结构物上的流体作用力分解为固定物体上的波浪绕射力和振荡运动结构物上的辐射力。Wu[1]基于势流理论，考虑线性自由面条件，对近水面淹没水平圆柱受迫振荡受力问题进行了理论解析，并将圆柱受力分解到了不同倍频上。Tyvand等[2]基于势流理论，考虑线性自由面条件，对近水面水平圆柱初始入水冲击问题进行了理论解析，分析了圆柱受力特征和自由面波动特征。上述基于势流理论的研究仅考虑线性自由面条件，考虑非线性自由面条件的相关研究也相继开展。Wu等[3]、Liu等[4]分别基于势流理论，考虑非线性自由面条件，对近自由面淹没水平圆柱受迫振荡问题进行了计算，考察了辐射波浪分布情况，分析了辐射波的非线性。Kent等[5]基于势流理论，考虑了非线性自由面条件，对淹没水平圆柱垂向受迫振荡的受力问题进行了数值研究，发现对于三倍频垂向力，其结果区别于Wu[1]的解析结果。Guerber等[6-7]基于势流理论建立了二维非线性数值水槽模型，并对淹没水平圆柱受迫振荡受力问题进行了数值计算研究，研究发现非线性自由面条件对二倍频力有影响。

由于上述研究基于势流理论忽略了流体黏性，无法对圆柱受力给出真实准确的计算结果；而仅考虑线性自由面条件也显然把问题理想化。因此，本研究有必要使用基于黏性流理论对淹没水平圆柱受迫振荡受力问题开展研究。本研究在Teng等[8-9]和毛鸿飞等[10-11]分别对波浪作用于淹没圆柱结构物和波浪对近水面结构物冲击作用问题研究的经验基础上，采用基于黏性流理论建立的数值波浪水槽模型开展计算研究，模型的基本控制方程为Navier-Stokes方程，方程的数值离散采用有限体积方法，自由面捕捉采用流体体积函数方法，数值造波和消波采用松弛区和速度边界结合方法，同时可以满足长时间计算需求。首先，对半淹没水平圆柱上的垂向波浪力进行了数值计算，与前人实验数据对比，验证数值模型对结构物上流体作用力计算的准确性。其次，对受迫振荡水平圆柱受力进行计算，将流体作用力并分解至多倍频项，考察其随振幅变化的特征规律，并将多个黏性流体下的受力结果与势流结果对比，分析黏性对各倍频流体作用力的影响规律。最后，将基于黏性流理论和势流理论得到圆柱上的压力以及黏性力幅值进行对比，结合圆柱周围黏性涡量场分布特征的分析，解释不同流体黏性下流体作用力差别原因。

1 数值模型

采用Navier-Stokes方程对不可压缩黏性流体的流动求解，其表示为：

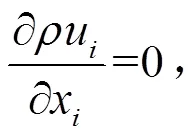
为了精确计算湍流流动，模型结合了RNG模型，其对流输运方程表示为：

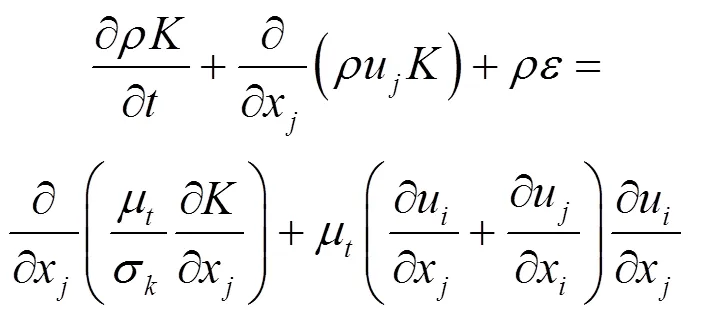
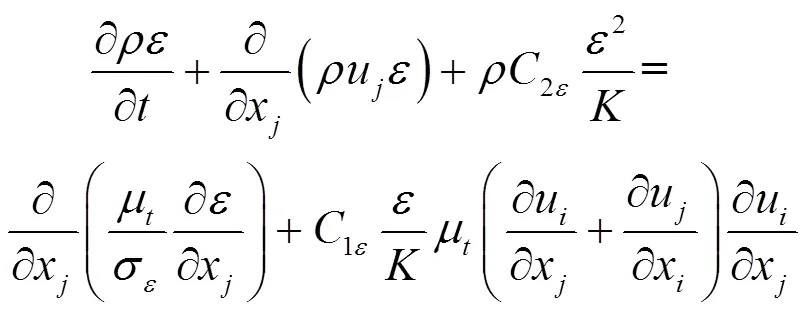
式中，为湍动能，为耗散率，1ε、2ε、σ、σ为模型常数。

对自由面的捕捉采用流体体积函数法，单元密度和黏性系数表示为：

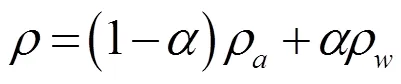
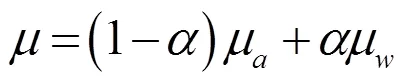
式中，为体积分数，气相中= 0，液相中= 1，自由面内= 0 ~ 1，ρ和ρ分别为液相和空气相的密度，μ和μ分别为液相和空气相的流体黏性系数。

为提高计算稳定性和界面分辨率，将人工压缩项引入界面方程，即

数值水槽模型采用速度边界法造波，结合松弛方法保证波浪稳定传输和消除反射，其设置如图1所示。协助波浪生产、稳定传播和吸收从结构物的一次反射浪的功能集成于松弛区I中，消除消波出口边界的二次反射波的功能集成于松弛区II中。

松弛区内，以解析形式修正数值求解，松弛修正需要借助如下松弛函数：

式中，为函数的关系函数，松弛函数的分布如图1所示。进而，松弛区内的数值修正可表达为：

式中，代表需要修正的物理量，即流体速度和体积分数，角标、分别表示解析值、计算值、目标值[13]。

构建数值波浪水槽模型首先需要对水槽和结构边界条件进行初始设置：将“速度边界条件”定义为“入口边界”，即边界上的流体速度始终按所需波浪理论给定，初始动态压强定义为*/= 0；将“可自由进出边界条件”定义为“顶边界”，即初始速度定义为∂u/= 0，初始动态压强定义为*= 0；将“不可滑移边界条件”定义为“出口边界”、“底边界”和“水槽中固定结构物边界”，即初始速度定义为u= 0，初始动态压强定义为*/= 0。

图1 边界条件

为实现强非线性波浪生产和传播功能，数值波浪水槽模型速度边界结合了五阶Stokes波浪理论控制模块。波面形式以及水平和垂向速度表达形式分别如式（10）、（11）和（12）所示，

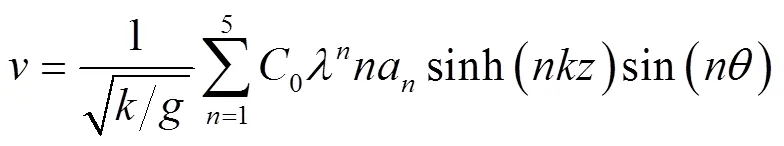
式中，I为松弛区I长度，为阶数，=为无量纲波幅，a和b为转化函数，为波数，为波幅，=（−I）−+为相位角，为波浪角频率，为初相位，B为与水深和波数相关的无量纲参数，0和A为与水深和相关的无量纲参数。上述无量纲参数及相关函数具体表达式可参考Fenton五阶Stokes波浪理论[14]。

通过上述数值方法获得压强和速度场分布后，结构物上的流体作用力可通过下式进行计算，

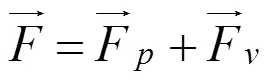
2 验证计算

2.1 计算设置

为了验证数值波浪水槽模型对结构物受流体作用力计算的准确性，根据Dixon等[15]的实验室物理模型试验，并参考前人[16-17]相关数值计算的设置，对半浅固定水平圆柱上垂向波浪力进行计算和对比验证，本研究的验证计算设置示意如图2所示。为水平圆柱半径，设置为0.125 m；为水深，设置为1.0 m，初始时刻轴心至于静水面处。速度边界的造波理论采用五阶Stokes波浪理论，波浪周期为1.646 s；波幅设置为0.125 m。圆柱水平位置，松弛区I和松弛区II的长度均根据入射波波长的一定比例进行设置。

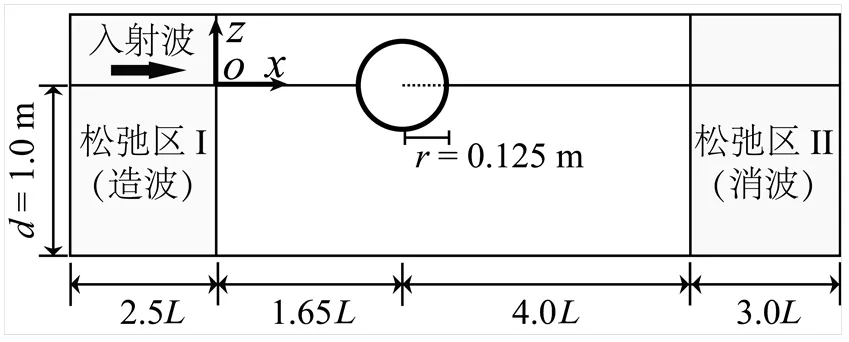
图2 验证计算示意图

2.2 波浪力验证对比

图3为采用本文数值模型计算获得的圆柱所受垂向波浪力数值结果与Dixon等[15]实验数据的对比情况。图中，无量纲垂向波浪力用z/(π2)表示，时间的无量纲形式表示为/（为入射波周期），考察一个周期内垂向波浪力的时间历程对比情况。通过观察可知，本研究数值结果与前人实验数据总体上吻合良好，这表明，该数值模型对结构物受力计算具有良好的准确性。

图3 一个周期内圆柱上的垂向波浪力

3 振荡圆柱上各倍频流体作用力

3.1 算例设置

本研究的黏性流数值计算根据Wu[1]考虑线性自由面条件的势流理论的解析研究条件，以及Guerber等[6-7]完全非线性的势流理论数值模拟研究条件进行设置，计算域如图4所示。圆柱分别在垂向方向和水平方向受迫振荡运动，振荡幅值用表示，圆柱半径为10 cm，水深设置为4.0 m。圆柱初始淹没深度，即圆心与静水面距离为0.3 m，为了消除反射波的影响，将松弛区II设置在水槽两侧，长度取2.5。

图4 计算域示意图

3.2 不同黏性下各倍频流体作用力对比

将本研究计算所得不同黏性下的黏性流数值结果与势流结果进行对比。用于对比的势流结果包括前人考虑线性自由面条件的理论解析结果，以及本文考虑非线性自由面条件采用高阶边界元方法计算所得到的数值结果，该数值计算方法参见Zhou等[18]。

为了获得圆柱上各频率的流体作用力分量，将流体作用力水平和垂向方向分量按照傅里叶级数形式进行分解，表达为：

式中，(0)为力的均值，(m)为倍频力，(m)为倍频分量的相位，下标和分别表示水平和垂向方向分量。考察各倍频流体作用力随振幅变化特征，并进行对比。为了对比和分析黏性影响，需排除其他参数的比例影响，将各倍频流体作用力按照无量纲形式(m)/(π22) 表示，将振幅按照无量纲形式/表示。

图5为圆柱在振荡方向上所受一倍频流体作用力的对比情况。从图中结果可见，对于小黏性工况，当振幅较小时，黏性流结果与势流结果比较接近；而当振幅较大时，出现黏性流结果逐渐小于势流结果的现象，且二者差距逐渐增大。对于大黏性工况，当振幅较小时，黏性流结果明显大于势流结果；当振幅较大时，无量纲的黏性流结果随着振幅增大出现先逐渐减小，而后逐渐增大的现象。两种不同黏性下的黏性流结果和势流结果之间均有明显差别，这说明一倍频流体作用力受到了流体黏性变化的显著影响。此外，自由面条件不同的势流结果非常接近，这表明线性自由面条件和非线性自由面条件对一倍频流体作用力的影响不显著。

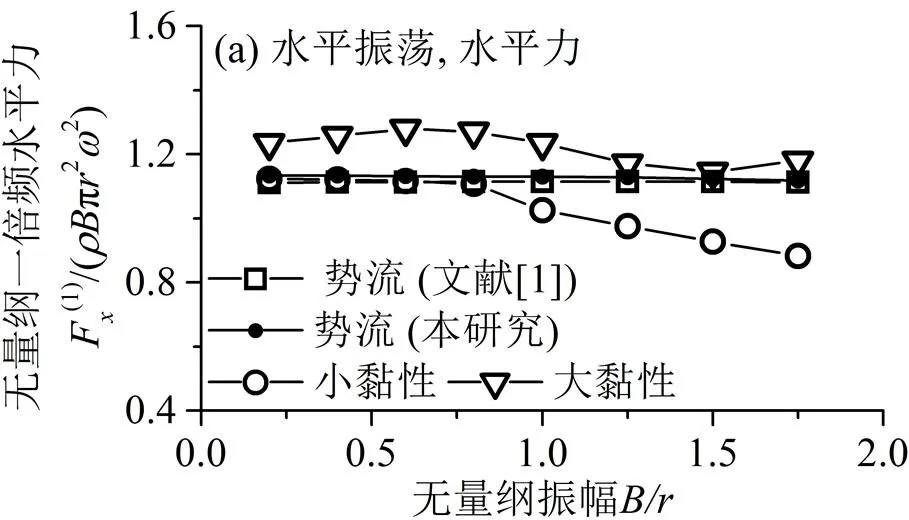
图5 振荡方向上的一倍频流体作用力

Fig. 5 The first harmonic components of the hydrodynamic forces in the oscillation direction

图6为圆柱在振荡方向上所受流体作用力的均值以及高倍频量的对比情况。从图中结果可见，相比之下，当振幅较大时，小黏性工况下的黏性流结果和考虑非线性自由面条件的势流结果总体上更为接近。大黏性工况下的黏性流结果与其他各组结果存在不同程度的差别，这表明，该情况下圆柱振荡方向上的流体作用力均值和高倍频量受到流体黏性变化不同程度的影响。此外，当振幅较大时，两组势流结果之间也存在一定差别，其原因为自由面条件的不同；也正是因为都考虑了非线性自由面条件，本研究小黏性工况黏性流结果与本文的势流结果更加接近，相比前人考虑线性自由面条件的势流结果在大振幅下有偏差。

图6 振荡方向上力的均值和高倍频量

Fig. 6 The mean and the high harmonic components of the hydrodynamic forces in the oscillation direction

图7为圆柱在水平振荡情况下所受垂向力均值和二倍频垂向力的对比。图中结果可见，当振幅较小时，不同黏性下的黏性流结果与势流结果均比较接近；而随着振幅增大，两次黏性流结果与势流结果之间的逐渐出现不同程度的差别，相比之下，大黏性工况下的黏性流结果与势流结果的差别相对更大一些。这表明，当振幅较大时，圆柱水平振荡情况下所受垂向力均值和二倍频垂向力均受到流体黏性变化的显著影响。此外，两组势流结果之间的差别原因仍为自由面条件不同。需要注意的是，水平振荡情况下圆柱所受垂向力均值并不为零，这是由于该情况下辐射波并不以振荡中心对称。

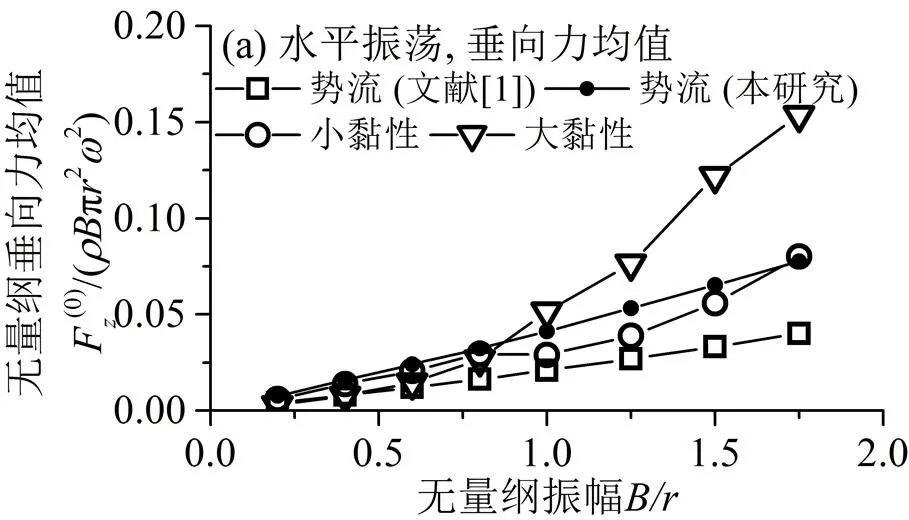
图7 水平振荡下垂向力均值和二倍频垂向力

Fig. 7 The mean vertical forces and the second harmonic components of the vertical forces

3.2 不同黏性下各倍频流体作用力对比

为了解释不同黏性的黏性流工况与本文考虑非线性自由面势流工况计算所得圆柱上流体作用力之间差别原因，并揭示黏性影响机理。以圆柱水平方向受迫振荡，不同黏性条件，/= 0.40，1.25和1.75工况为例，将流体作用力分解为压力和黏性力，从而进行对比，并对圆柱附近黏性涡量场分布特征进行分析。

图8为将圆柱所受流体作用力分解后的压力和黏性力时间历程对比情况。从对比结果可见，/= 0.40工况下，对于压力，两组黏性流结果与势流结果的幅值很接近，说明流体黏性对压力影响不显著。/= 1.25工况下，对于压力，两组黏性流结果的幅值均小于势流结果。/= 1.75工况下，对于压力，小黏性工况下的压力幅值小于势流下的压力，而大黏性工况下的压力幅值大于势流下的压力。在本文所考察的工况下，对于黏性力，小黏性工况下的黏性力远小于压力，相比之下，大黏性工况下的黏性力对总流体作用力的贡献相对较大。

图9为水平压力为负极值时圆柱附近黏性流涡量场。图中，“Vorticity”为涡量，可表达为=(∂∂−∂∂)/(/)，其中为流速大小，为圆柱直径；“F”为惯性力，箭头指向表示流体相对加速度的方向；“S”和“L”分别代表小黏性工况和大黏性工况，对应的数值为无量纲振幅/值。从图9-a和9-d可见，两种黏性小振幅下，圆柱附近无明显的涡旋产生。从图9-b、9-c和9-e可见，随着振幅增大，贴体涡旋出现圆柱加速度方向相反一侧。从图9-f可见，涡旋运动相比圆柱运动滞后性更强，此刻的涡旋位置发生明显改变。同时，可以判断，随着振幅和黏性增大，涡旋压力在流体作用力中的作用和占比也会发生变化。另外，需要注意的是，圆柱上下涡旋均为明显的非对称分布。

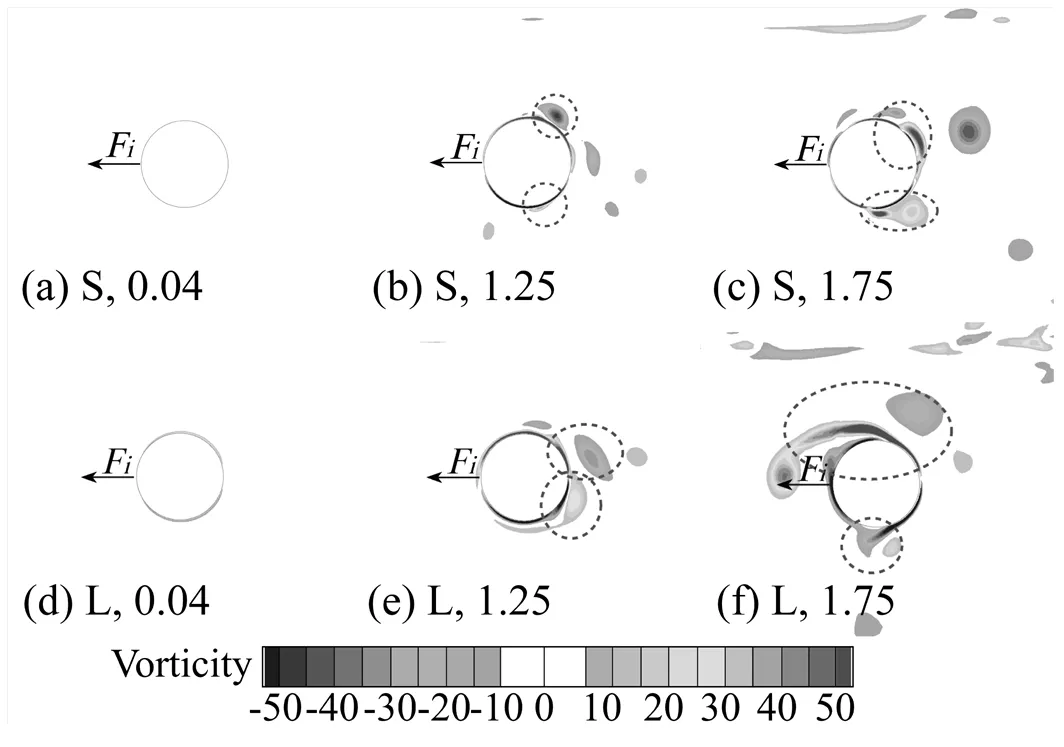
图9 水平压力为负极值时的圆柱周围涡量场

为了更直观说明涡旋对圆柱表面压力的影响，将/= 0.40和1.75下，水平压力达到负极值时圆柱表面压强分布进行对比，如图10所示。其中，图10-a为对圆柱表面环向角度的定义，Angel表示环向角度。从图10-b压强对比结果可见，曲线的凹陷出现在贴体涡旋对应位置（图9），且在大黏性工况下，曲线凹陷范围较大，曲线在水平方向上的积分面积较大。这表明，在小黏性，/= 1.75工况下，由于涡旋压强始终小于周围压强，则其减小了圆柱表面正压侧表面压强。由于涡旋压力的幅值相对较小，黏性流下的压力幅值小于势流下的压力幅值，无量纲一倍频力呈现随振幅增大而逐渐减小的趋势（/= 0.80 ~ 1.75）；在大黏性，/= 1.75工况下，涡旋压力幅值相对较大，并在圆柱所受压力占比中起主导作用，使黏性流下圆柱所受压力幅值增大至大于势流结果，因而无量纲一倍频力呈现随振幅增大而逐渐增大的趋势（/= 1.50 ~ 1.75）。

通过上述分析可以得知，对于一倍频流体作用力，小黏性工况，大振幅下，由于涡旋压力的存在，圆柱所受压力幅值相比势流结果较小，黏性流下一倍频力随振幅增大逐渐小于势流结果，二者之间差距也逐渐增大。大黏性工况，小振幅下，由于黏性力的贡献相对较大，黏性流一倍频流体作用力大于势流结果，而随着振幅增大，贴体涡旋由起减小圆柱所受压力作用转为增大压力的作用，因而黏性流下一倍频力无量纲结果呈现先减小后增大的趋势。对于振荡方向上的均值力和高倍频力，大黏性下黏性流和势流结果之间有明显差别，这是因为此时黏性力对流体作用力贡献较大，即黏性力的均值和高倍频分量对总的流体作用力所造成的影响。水平振荡下的垂向力均值和二倍频垂向力，在圆柱大幅水平振荡情况下，受到自由面波动的影响，圆柱上下所产生的涡旋为非对称分布，导致了两组黏性流结果与势流结果有不同程度的差别。

4 结论

本研究对流体黏性对自由面下受迫振荡水平圆柱所受流体作用力特征的影响开展了黏性流数值计算研究，研究结论总结如下：

（1）对于振荡方向上的一倍频力，两组黏性流结果与势流结果均有明显差别，其原因为大幅振幅下涡旋的产生对于圆柱表面压力造成的影响，以及大黏性工况下黏性力对流体作用力的贡献较大。

（2）对于振荡方向上力的均值和高倍频力，大黏性工况结果与其他各组结果有明显差别，其原因为黏性力的贡献较大，黏性力的均值和高倍频分量对总流体作用力有影响。

（3）对于水平振荡下的垂向力均值和二倍频垂向力，大幅振荡下，两组黏性流结果均与势流结果有差别，并且大黏性工况下差别更明显，其原因为在自由面影响下，圆柱上下涡旋分布不对称对圆柱所受垂向压力有影响。

[1] WU G X. Hydrodynamic forces on a submerged circular cylinder undergoing large-amplitude motion[J]. Journal of Fluid Mechanics, 1993, 254: 41-58.

[2] TYVAND P A, MILOH T. Free-surface flow due to impulsive motion of a submerged circular cylinder[J]. Journal of Fluid Mechanics, 1995, 286: 67-101.

[3] WU G X, EATOCK TAYLOR R. Time stepping solutions of the two-dimensional nonlinear wave radiation problem[J]. Ocean Engineering, 1995, 22(8): 785-798.

[4] LIU Y M, ZHU Q, YUE D K P. Nonlinear radiated and diffracted waves due to the motions of a submerged circular cylinder[J]. Journal of Fluid Mechanics, 1999, 382: 263-282.

[5] KENT C P, CHOI W. An explicit formulation for the evolution of nonlinear surface waves interacting with a submerged body[J]. International Journal for Numerical Methods in Fluids, 2007, 55(11):1019-1038.

[6] GUERBER E, BENOIT M, GRILLI S T, et al. Modeling of fully nonlinear wave interactions with moving submerged structures[C/OL]. Proceedings of the International Offshore and Polar Engineering Conference, 2010, 529-536.

[7] GUERBER E, BENOIT M, GRILLI S T, et al. A fully nonlinear implicit model for wave interactions with submerged structures in forced or free motion[J]. Engineering Analysis with Boundary Elements, 2012, 36(7): 1151-1163.

[8] TENG B, MAO H F, LU L. Viscous effects on wave forces on a submerged horizontal circular cylinder[J]. China Ocean Engineering, 2018, 32(3): 245-255.

[9] TENG B, MAO H F, NING D Z, et al. Viscous numerical examination of hydrodynamic forces on a submerged horizontal circular cylinder undergoing forced oscillation[J]. Journal of Hydrodynamics, 2019, 31(5): 887-899.

[10] 毛鸿飞, 陈洪洲. 非完全淹没水平圆柱上波浪力特征的数值模拟[J]. 水科学进展, 2019, 30(5): 749-759.

[11] 毛鸿飞, 李芳成, 吴光林，等. 基于黏性流理论对平板受波浪冲击的两相流数值研究[J]. 广东海洋大学学报, 2019, 39(4): 73-80.

[12] WELLER H G, TABOR G, JASAK H, et al. A tensorial approach to computational continuum mechanics using object oriented techniques[J]. Computers in Physics, 1998, 12(6): 620-631.

[13] JACOBSEN N G, FUHRMAN D R, FREDSØE J. A wave generation toolbox for the open-source CFD library: OpenFoam® [J]. International Journal for Numerical Methods in Fluids, 2012, 70(9): 1073-1088.

[14] FENTON J D. A fifth-order Stokes theory for steady waves[J]. Journal of Waterway, Port, Coastal and Ocean Engineering-asce, 1985, 111(2): 216-234.

[15] GRAHAM DIXON A, GREATED C A, SALTER S H. Wave forces on partially submerged cylinders[J]. Journal of the Waterway Port, Coastal and Ocean Division, 1979, 105(4): 421-438.

[16] WESTPHALEN J, GREAVES D M, WILLIAMS C K, et al. Extreme Wave Loading on Offshore Wave Energy Devices using CFD: A Hierarchical Team Approach[C/OL]. Proceedings of European Wave and Tidal Energy. Uppsala, Sweden, 2009.

[17] HU Z, CAUSON D M, MINGHAM C G, et al. Numerical simulation of floating bodies in extreme free surface waves[J]. Natural Hazards and Earth System Sciences, 2011, 11(2): 519-527.

[18] ZHOU B Z, NING D Z, TENG B, et al. The numerical simulation of fully nonlinear deep-water waves[J]. Acta Oceanologica Sinica, 2011, 33(1): 27-35.

Viscous Effects on Hydrodynamic Forces on a Horizontal Circular Cylinder under Forced Oscillation

YUAN Jian-ping1, MAO Hong-fei1, HE Yan-li1, PAN Xin-xiang2, JIA Bao-zhu2

（1.,,524088,;2.,,524088,）

【Objective】To accurately predict the hydrodynamic force of a circular structure under viscous fluid effects.【Method】A viscous fluid numerical wave tank model was established by using the finite volume method. Firstly, the accuracy of the numerical model was validated against available experimental data for the wave forces on a semi-submerged circular cylinder. Secondly, the viscous numerical calculations for different fluid viscosities were carried out. The comparisons of the hydrodynamic forces on the circular cylinder predicted by the viscous fluid model and the potential flow model were conducted to show the viscous effects on the hydrodynamic forces.Finally, by studying the components of the pressure forces and the viscous shear forces, and by analyzing the vorticity fields around the cylinder, the reasons for the differences between the results based on the viscous fluid theory and the potential flow theory were explained.【Result】There are different degrees of differences among the harmonic components of the hydrodynamic forces on the horizontal circular cylinder under different viscosities.【Conclusion】The numerical results predicted by the viscous fluid model are more accurate than those from the potential flow models.

circular cylinder; forced oscillation; hydrodynamic forces; numerical simulation; wave tank

TV139.2+6

A

1673-9159（2020）04-0116-08

10.3969/j.issn.1673-9159.2020.04.016

2020-04-10

广东省自然科学基金（51979045，51479017）；国家装备预研基金项目（6142204190711）；国家国防科工局稳定支持课题（JCKYS2019604SXJQR-02）；广东省教育厅重点领域专项（2019KZDZX1024）；广东省教育厅高校青年创新人才项目（2019KQNCX045）；广东海洋大学科研启动费项目（120602-R19024）；广东省“冲一流”省财政专项资金建设项目（231419010）

袁剑平（1979－），男，硕士，高级工程师，研究方向为船舶智能控制系统开发。E-mail: yjp_103@163.com

毛鸿飞（1985－），男，博士，讲师，研究方向为波浪与结构物的相互作用。E-mail：maohongfei-gdou@qq.com

袁剑平，毛鸿飞，赫岩莉，等. 流体黏性对受迫振荡水平圆柱受力的影响[J].广东海洋大学学报，2020，40（4）：116-123.

（责任编辑：刘朏）