基于TDIC的上海市奉贤区大气能见度变化特征分析
周建康, 顾品强, 汤晨阳, 邱 翔, 李家骅, 李 磊
(1. 上海应用技术大学 a. 机械工程学院; b. 理学院; c. 城市建设与安全工程学院, 上海 201418;2. 上海市奉贤区气象局, 上海 201416)
根据世界气象组织的定义,能见度是指正常视力的人在白天天气情况下,能够从天气背景中看到和辨认出适当大小黑色目标物的最大距离,在夜间则指假设亮度与白天相同条件下,能够辨认出目标物的最大距离[1]。
在低能见度天气条件下,大气颗粒物容易形成二次污染物,从而直接危害人们的身体健康,给日常生活带来许多不便[2]。同时,低能见度天气常常是造成交通事故和突发事件的重要原因。孙冉等[3]研究了上海市在雾、霾等天气过程,不同天气现象的气溶胶光学特性,以及能见度的影响因素。徐薇等[4]探究上海市能见度与和散射系数之间的关系。姜江等[5]分析了北京市能见度的影响因素,主要为相对湿度、风速和浓度。古金霞等[6]研究了济南市能见度变化特征,大气能见度主要受相对湿度和细颗粒物质量浓度的影响。施悯悯等[7]对合肥市大气能见度研究发现,不同相对湿度下,颗粒物浓度对大气能见度的影响不同。
气象要素变化和大气污染物浓度变化存在多层次时间尺度结构,变化也具有非线性、非平稳特征,用传统的信号分析方法不能真实地描述各因素之间的变化关系。1998年,Huang等[8]提出了经验模态分解(empirical mode decomposition,EMD)方法。EMD与传统信号分析方法不同,该方法不预设基函数,而是预设好判断,基于信号本身所含有的特征尺度进行分解,具有比较明确的物理意义。2008年,Huang等[9]提出了Hilbert-Huang变换(Hilbert-Huang transform,HHT),HHT方法对非线性、非平稳数据处理得到更加符合物理的解释和说明,具有自适应的特点。Chen等[10]在2010年提出了一种确定2个时间序列的尺度相关关系的方法,即时间内在关联分析法(time dependent intrinsic correlation, TDIC)。TDIC根据多尺度复杂信号提供不同的自适应窗口,同时,引入多个物理参数对复杂数据进行多尺度分析,从整体和局部上更清楚的观察2组数据之间的相关关系以及物理过程。Huang等[11]用TDIC方法分析了海洋中溶解氧与温度之间的相关关系,研究了温度与海洋数据之间复杂的关系。Sankaran等[12]使用TDIC方法分析了Kallada河流中水流流速与水中悬浮沉淀物浓度的变化关系,Dhouha等[13]利用TDIC分析了Reunion岛上温度与其他环境要素的相关关系, Adarsh等[14]根据HHT和TDIC分析了印度雨季降雨的多尺度特征以及对降雨的预测。
本文在分析奉贤区能见度变化特征的基础上,利用TDIC重点分析了能见度与相对湿度、能见度与浓度变化、能见度与浓度变化之间的相关关系,进一步探究大气能见度的变化特征。
1 资料与方法
1.1 资料
数据资料由上海市奉贤区气象局提供,研究数据为上海市奉贤区2008~2017年的气象数据和2015~2017年的空气质量监测数据。采用上海市国家基本气象站逐小时地面观测数据(包括能见度、相对湿度、浓度数据等),采样时间分辨率为1 h。所有数据均进行严格的质量控制,删除异常值,对于缺失数据使用点处线性趋势插值法进行处理。
1.2 HHT方法
采用Huang等[8]提出的经验模态分解方法(empirical mode decomposition,EMD),分析2008年1月~2017年12月大气能见度、相对湿度和大气污染颗粒物数据,逐级分解出固有模态函数(intrinsic mode functions,IMF)分量,将分解后的每个IMF分量进行Hilbert变换,得到原始信号的时频分布,从而观察原始数据的多尺度变化。
内模函数的定义[8-9]:① 极值点的个数与过零点数目相等,或最多相差1;② 在任意一点,由极大值构成的包络与极小值构成的包络的平均值为0。
这样就把原始的信号分解为一系列的内模函数IMF和残余项r(t):
(1)
对分解后的每一阶IMF进行Hilbert变换,得到相应的解析信号:
ai(t)ejφi(t)
(2)
P表示取Hilbert变换的主值,对应的瞬时频率为:
(3)
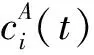
(4)
这样就将原信号表示为有限阶内模函数的叠加:
(5)
由式(5)可见,HHT方法分解得原始数据频率调制和幅值调制信息,这也是对傅里叶分析和小波分析的创新。得到的结果将时间、频率和能量的关系式H(ω,t)绘在一起,得到Hilbert谱图。
1.3 TDIC方法
传统的相关性分析方法,处理非线性数据可能会曲解数据之间的相关关系,忽视真实的物理过程[15-16]。TDIC方法基于EMD分解,根据每个IMF分量的瞬时周期,决定每个信号模态的自适应窗口大小[10]。在进行TDIC方法分析的时候,首先使用EMD将2个时间序列分解成不同尺度的模态,其次比较2个时间序列的平均周期,并选择平均周期几乎相等的2个IMF分量进行TDIC分析。
假设有2个分量IMF1和IMF2,它们的平均周期几乎相同,但属于不同的时间序列,这2个分量的相关性可以这样估算:
(6)

td=max(T1i(tk),T1j(tk))
(7)
式中:T1i和T1j是瞬时周期;T=w-1;n为任何正整数[11]。
2 奉贤区大气能见度的变化特征
2.1 日变化特征
图1为2008年1月~2017年12月上海市奉贤区1、4、7和10月小时平均能见度变化。为研究奉贤区不同季节能见度变化特征,将季节划分为春季(3、4、5月)、夏季(6、7、8月)、秋季(9、10、11月)和冬季(12月、次年1、2月),并选取每个季节的中间一个月,即1、4、7和10月作为冬季、春季、夏季和秋季的代表月[2]。
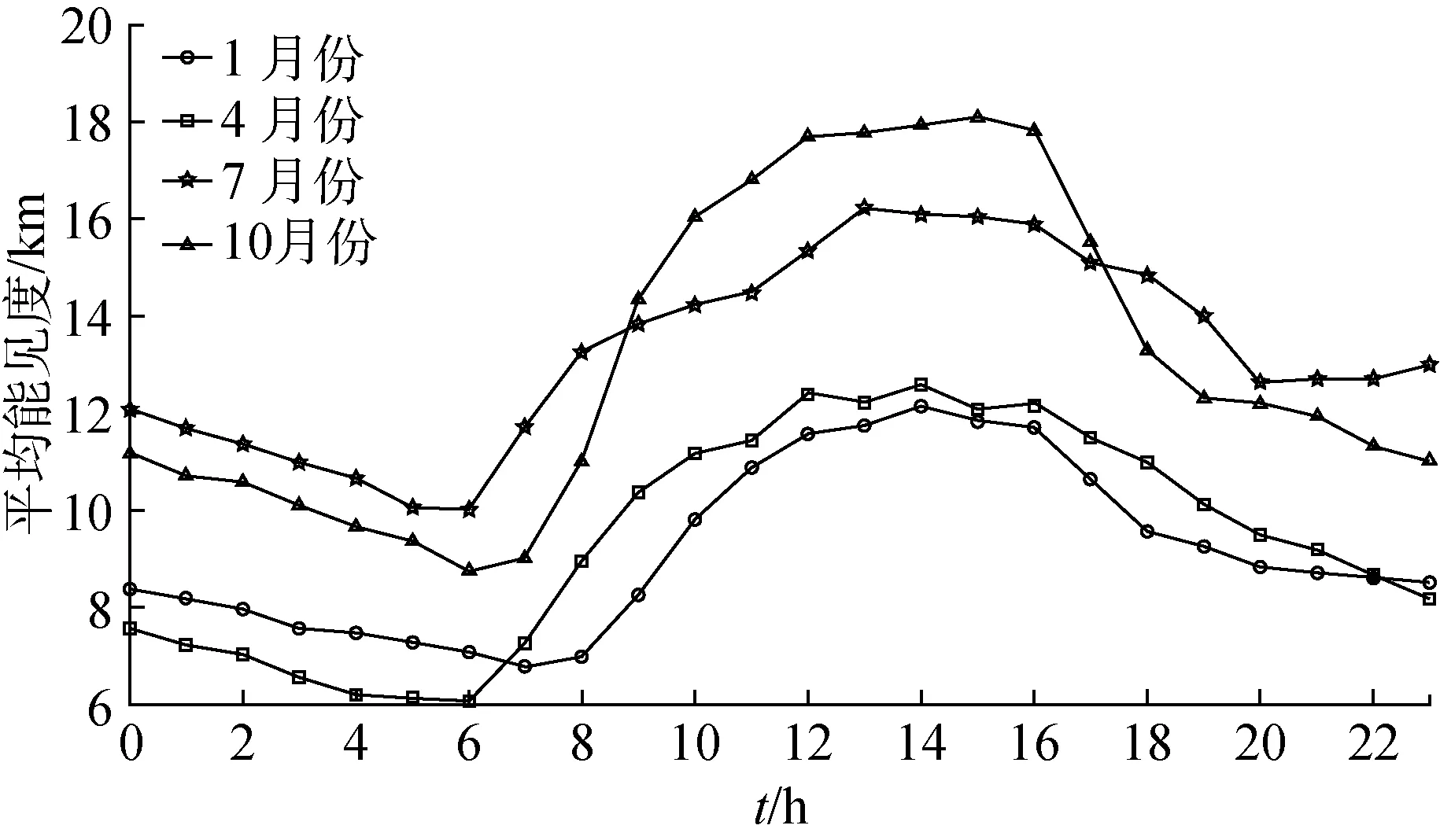
图1 上海市奉贤区1、4、7和10月小时平均能见度日变化Fig.1 Daily variation of hourly average visibility in January, April, July and October in Fengxian District of Shanghai
通过对上海市奉贤区正点观测能见度数值分析发现,日均大气能见度最小值为503.6 m,最大值为35.78 km,平均值为10.86 km,日变化幅度为35.27 km,大气能见度具有明显的日变化特征。日出前后6~7时为一天中能见度最差的时段,这可能由于夜间大气层结构较为稳定,大气湍流强度较弱,再加上早晨因炊事,交通等人类活动较为集中,这都导致了从夜间到早晨能见度的降低;日出之后的3~5 h随着光照辐射的增强,气温的回升,相对湿度减小,而且大气湍流强度逐渐增强,使得大气能见度上升迅速,因此13∶00~14∶00时能见度达到一天中最高值;傍晚光照辐射减弱,气温下降,相对湿度逐渐增大,大气能见度迅速降低,到了夜间,能见度缓慢下降。
2.2 季节变化特征
图2为2008~2017年,10年间4个季节小时平均能见度。
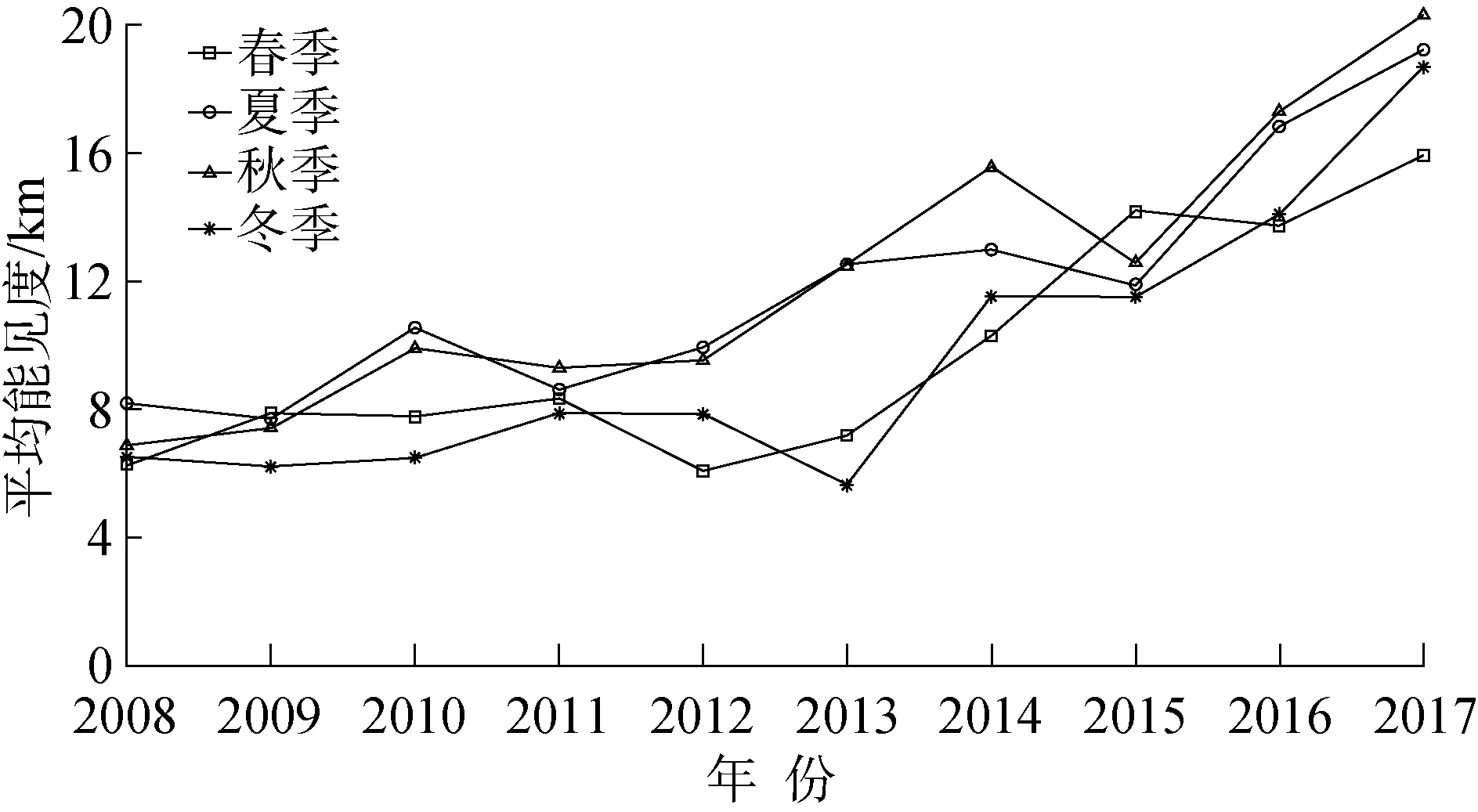
图2 4个季节小时平均能见度Fig.2 Average hourly visibility per season
结合图1、图2分析发现,在2008~2017年10年间,上海市奉贤区各个季节能见度的日变化趋势大体上是一致的。

表1 2008~2017年各季度日平均能见度Tab.1 Daily average visibility for each quarter in 2008-2017
表1是2008~2017年各季日平均能见度统计结果。由表1可见,日均能见度秋季最高,夏季次之,冬季最低。进入夏季,太阳辐射时间增长,温度较高,能见度较高,而受梅雨天气影响,在6月中旬到7月中旬,上海的降水量增加,相对湿度增大,会影响能见度的上升;进入秋季,相对湿度减小,风速增大,能见度上升。冬季对流运动变弱,空气交换速度变慢,并且雾、霾等天气频繁,能见度随之变差。这一特征与我长三角地区城市能见度冬、春季较差,夏、秋季较好的一般规律相同[17-19]。
2.3 年际变化特征
图3为对2008~2017年上海市奉贤区日均能见度进行EMD分析。由图3可得到10个IMF分量和趋势分量残余函数(residual function,RES)。每个IMF分量依次反映了原始信号从高频到低频不同时间尺度上的波动特征,最后得到的趋势项RES表示,原始信号总体随时间变化的趋势。在10年期间,奉贤区日均能见度呈小幅度上升趋势。每个IMF分量具有相对稳定的准周期,不同时间尺度的IMF分量周期性呈现非均匀变化,反映了能见度变化受到大气内部运动和外部因素共同作用的影响。
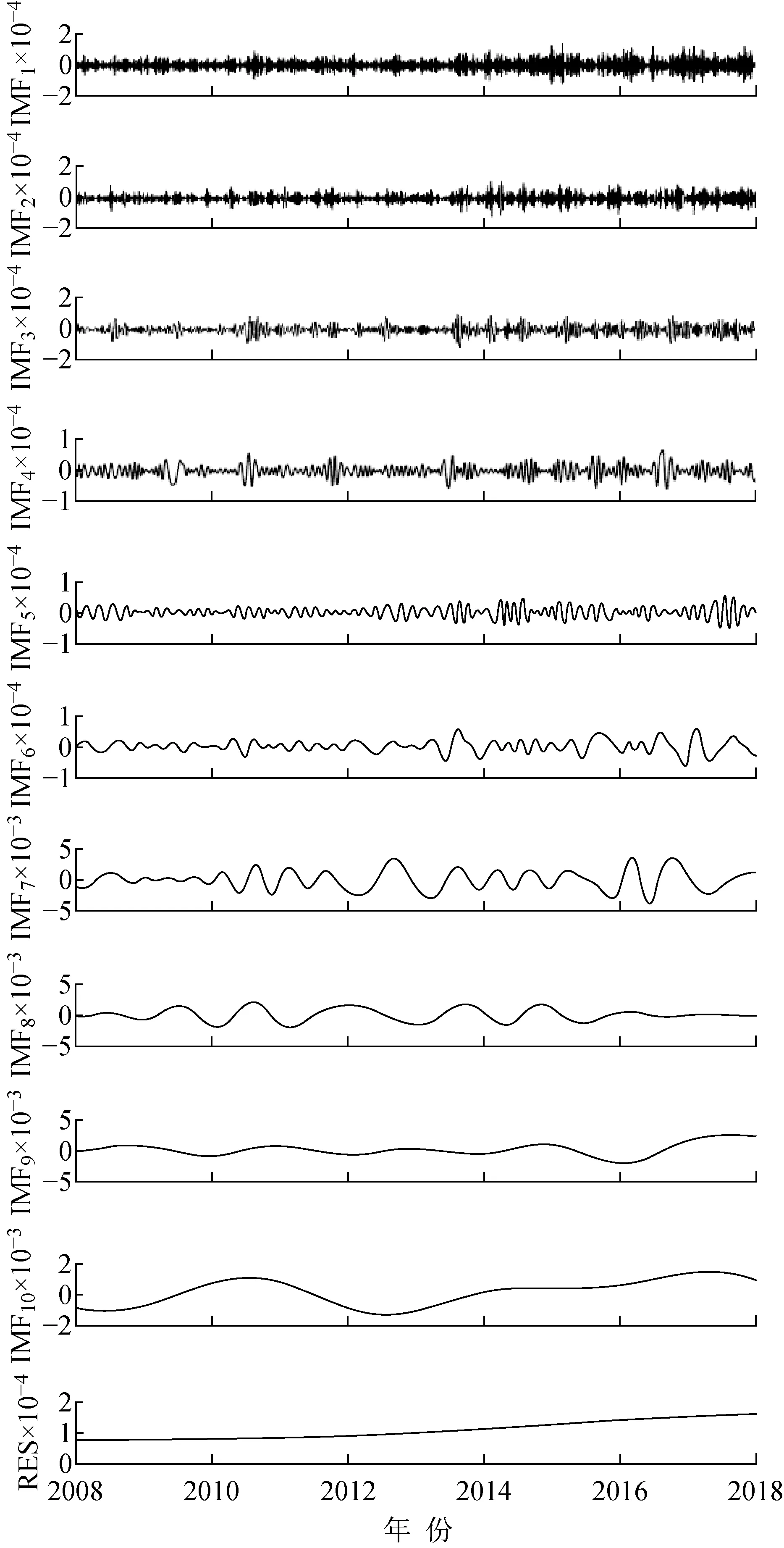
图3 2008~2017年奉贤区日均能见度时间序列EMD分析Fig.3 EMD analysis of daily visibility time series in Fengxian District in 2008-2017
图4给出了能见度序列的Hilbert谱,显示了不同频率信号的振幅能量随时间的变化。能见度值随时间有上升的趋势,相应的Hilbert谱的波动振幅随时间有逐渐增大的趋势,频率波动相对比较剧烈的时刻对应的Hilbert能量波动较强。
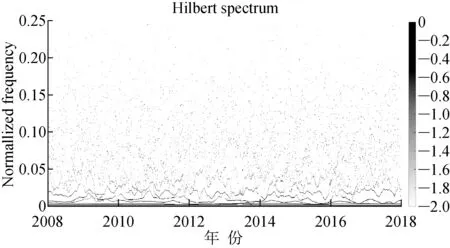
图4 2008~2017年能见度时间序列Hilbert谱Fig.4 Visibility time series Hilbert spectrum in 2008-2017
3 奉贤区大气能见度影响因素分析
3.1 能见度主要影响因子
有关研究表明[5-6],大气能见度的大小受到相对湿度、风速、温度、气压等气象条件的影响,还要受到大气污染颗粒物(PM2.5、PM10)的影响。表2为能见度的主要影响因子与能见度变化的相关系数,在全年范围内,PM2.5浓度与能见度相关性最强,相对湿度(RH)次之,PM10浓度与能见度相关性最低。秋冬季节,大气污染颗粒物与能见度相关系数较高;在春季和夏季,RH与大气能见度的相关系数较高。
表2 主要影响因子与能见度变化的相关系数
Tab.2 Correlation coefficient between meteorological parameter and visibility change

时间PM2.5PM10RH全年-0.575 8-0.398 4-0.519 7春季-0.485 1-0.165 9-0.601 2夏季-0.055 2-0.392 7-0.567 6秋季-0.693 6-0.469 4-0.585 9冬季-0.652 1-0.398 4-0.553 7
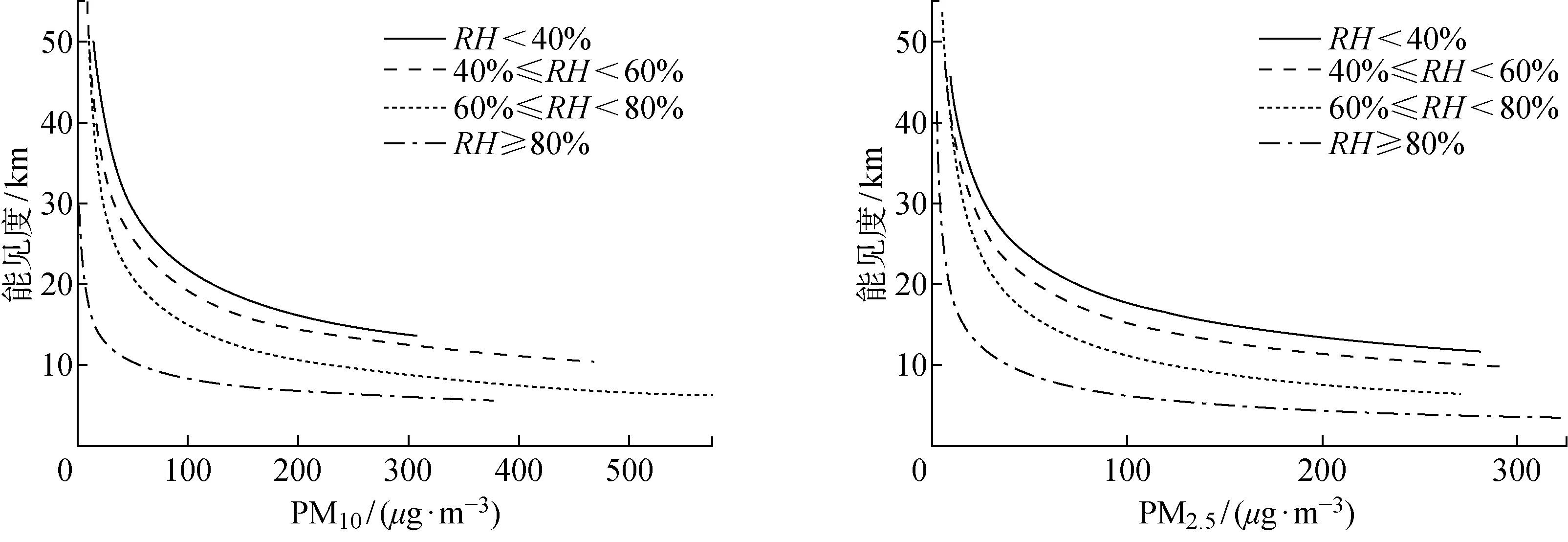
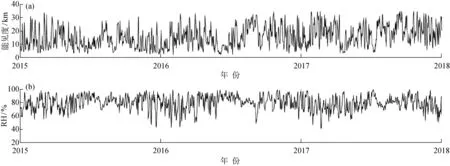
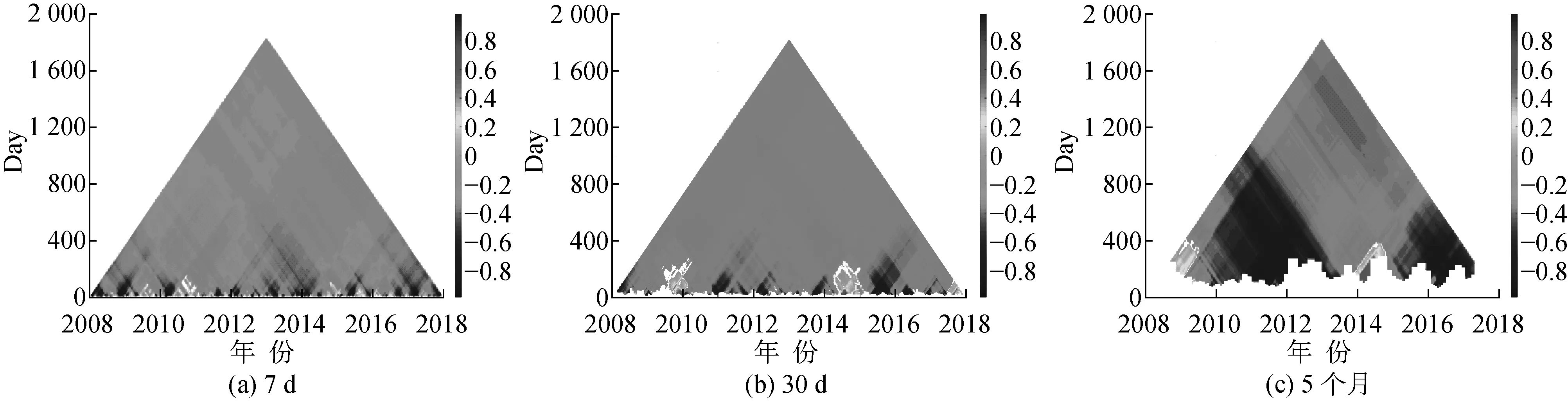
图5为不同RH下大气能见度与PM10、PM2.5浓度的变化关系,把RH分为RH<40%,40% 图6为2015~2017年RH与能见度的变化趋势。其中:图6(a)为能见度的变化趋势;图6(b)为RH的变化趋势。 为了更详细的描述RH与能见度的相关关系,采用时间相关的TDIC,数据选取2008~2017年RH和能见度数据,在2008~2017年期间,分为 7 d、30 d、5个月等周期对能见度与RH相关性分析。 图7为能见度与RH的TDIC图。其中:图7(a)为能见度与RH在周期为7 d的TDIC图,能见度与RH具有丰富的相关性特征,呈现负相关性,整体相关系数为 -0.325 1;图7(b)为能见度与RH在周期为30 d的TDIC图,能见度与RH在窗口尺寸<60 d时呈现正相关性;图7(c)为能见度与RH在周期为5个月的TDIC图。由图可见,在2014年6~9月,出现高强度降水天气,能见度和RH具有弱的正相关性,相关系数为0.4,这种从由负相关性转变到正相关性还受到降水、风速、大气污染物浓度变化等因素的共同影响。 研究表明[6-7],大气中高浓度的颗粒物是造成大气能见度下降的重要原因,它们通过散射和吸收消光作用来降低能见度。本文利用2015~2017年期间日平均能见度和PM10、PM2.5浓度资料。 图8为能见度、PM10、PM2.5在2015~2017年的变化图。其中:图8(a)显示日均能见度的变化趋势;图8(b)显示日均PM10浓度的变化趋势;图8(c)显示日均PM2.5浓度的变化趋势。由图8可见,能见度与PM10浓度、PM2.5浓度变化呈现负相关变化趋势。 图5 不同相对湿度下大气能见度与PM10、PM2.5浓度的变化关系Fig.5 Relationship between atmospheric visibility and concentration of PM10 and PM2.5 at different relative humidity 图6 2015~2017年能见度及相对湿度的变化趋势Fig.6 Trends in visibility and relative humidity in 2015-2017 图7 能见度与RH的TDIC图Fig.7 TDIC plot between visibility and relative humidity 图8 能见度、PM10、PM2.5在2015~2017年的变化图Fig.8 The variation diagram of visibility, PM10 and PM2.5 in 2015~2017 图9 PM10浓度与能见度的TDIC图Fig.9 TDIC plot between PM10 and visibility 3.3.1 PM10浓度与能见度的TDIC分析结果 图9(a)为PM10浓度与能见度在周期为7 d的TDIC图,图9(b)为PM10浓度与能见度在周期为30 d的TDIC图。2015~2017年,日均能见度与PM10浓度变化呈现负相关。从图9(a)、(b)可以看出,在2015年4~7月、2016年10月~2017年1月等局部时间范围,能见度与PM10浓度由负相关性转变为正相关性,这种变化受到复杂天气状况影响,如高强度降水、持久雾霾等极端天气,都会影响能见度与污染物浓度的关系。 3.3.2 PM2.5浓度与能见度的TDIC分析结果 图10为能见度与PM2.5浓度的TDIC图。在图10(a)中,能见度与PM2.5浓度存在较强的相关关系。图10(b)中,2015年10~11月,能见度与PM2.5浓度在窗口尺寸小于7 d时具有正相关性,2016年11月~2017年1月,能见度与PM2.5浓度在窗口尺寸小于30 d时具有正相性。在这2个时间段中RH比全年平均相对湿度高1.2%,高相对湿度,影响颗粒物浓度对能见度的作用,同时相关性变化还会受到降水、风速、大气污染物浓度变化等因素的共同作用。由图9和图10可以发现,大气能见度与PM2.5浓度变化的相关系数明显高于PM10。 图10 PM2.5浓度与能见度的TDIC图Fig.10 TDIC plot between PM2.5 and visibility (1) 上海市奉贤区大气能见度平均日变化和季节变化趋势明显,日均能见度最高值出现在 13∶00~14∶00时,最低值出现在6∶00~7∶00时,日变化最大幅度为35.27 km,大气能见度季节变化为秋季>夏季>春季>冬季,10年期间,能见度有逐渐上升的趋势。 (2) 在不同的相对湿度下,颗粒物浓度对大气能见度的影响不同。当RH较高时(RH≥80%),气溶胶颗粒的吸湿潮解作用会发生改变,颗粒物浓度对能见度影响力减弱,能见度主要受到相对湿度的影响。颗粒物浓度的减少对能见度的影响有不同的阶段性,当颗粒物浓度大于75 μg·m-3时,颗粒物浓度的减小对能见度的影响不明显;当颗粒物浓度小于50 μg·m-3时,能见度随着颗粒物浓度的上升快速下降。 (3) 利用TDIC对能见度与RH、PM10和PM2.5浓度变化进行相关性分析。能见度与RH变化之间存在负相关性,在2014年6~9月时间范围内,能见度与RH相关关系由负相关性变为正相关性,这种变化受到降水、风速、大气污染物等因素和高强度降水天气的共同影响;能见度与PM10和PM2.5浓度之间存在着强的负相关性,并且PM2.5对大气能见度的影响大于PM10,在2015年10~11月、2016年11月~2017年1月等局部时间内,能见度与颗粒物浓度呈现正相关性,在此期间,相对湿度比全年相对湿度高1.2%,高相对湿度影响颗粒物浓度对能见度的作用,同时相关性变化还会受到高强度降水、持久雾霾等极端天气的影响。3.2 相对湿度对能见度的影响
3.3 大气污染颗粒物对能见度的影响



4 结 语

