基于主成分分析和代理模型的油藏生产注采优化方法

张 凯, 陈国栋, 薛小明, 张黎明, 孙 海, 姚传进

(中国石油大学(华东)石油工程学院,山东青岛 266580)

目前,新油田发现的数量逐年递减,世界各地许多大型油田产量也在逐年下降。如何立足现有条件,通过对各单井流量进行调控,使注入水流入未波及的区域,以提高油藏采收率、最大化油藏开发潜力至关重要。近年来生产优化领域算法可以分为梯度优化算法和无梯度算法。基于梯度的优化方法[1-2](如序列二次规划[3-4])使用伴随方法来获得梯度信息。然而,基于梯度的优化方法容易陷入局部最优,梯度获取困难。无梯度方法可以进一步划分为近似梯度算法(如SPSA算法[5]和En-Opt算法[6])和启发式算法(如粒子群算法[7]和人工蜂群算法(ABC)[8])。近似梯度算法[9-11]可以计算近似的数值梯度,不需要使用伴随方法。启发式算法全局性好,可获得更高的油藏开发经济效益,但需要大量数值模拟调用次数。基于代理模型的进化算法在油藏生产优化问题中可以减少数值模拟调用次数降低时间成本[12]。因此近年来研究者提出了很多基于代理模型的算法来解决生产优化问题[13-14],如多项式响应面模型[15]、克里金模型[16]、人工神经网络[17]和径向基函数[18]。然而,代理模型在构建模型时计算量大,处理高维问题时性能恶化[19]。Regis[20]提出基于克里金模型构建代理的方法主要应用于少于15个决策变量的问题。为解决上述问题,笔者提出结合代理模型和降维算法的新框架解决生产优化问题,并将油藏模型实例结果与现有进化算法和直接代理优化进行对比分析。

1 油藏生产优化问题

油藏生产优化通过调整油水井的注采参数改变地下流体的分布状态,提高油藏波及系数,以最大化目标函数(如净现值(NPV)或累积产油量),进而实现生产效益最大化[21-22]。由于决策变量和目标函数之间的非线性关系,找到油水井最优注采方案是一项具有挑战性的工作。生产优化问题的目标是找到最优控制变量组xm×n,其中m为井的数量,n为控制时间步数。因此变量的数量等于待优化井数乘以控制时间步数。

油田开发的主要目的是经济效益最大化,因此结合最优控制理论,以净现值作为生产优化性能指标,得到简化的目标函数表达式为

f(x,y)=NPV(x,y)=

(1)

约束条件为

c(x)≤0,

(2)

x1≤x≤xu.

(3)

式中,x为要优化的变量组,即井控参数向量(如井底压力或油水井流量);y为状态参数矩阵,如油藏模型所有网格的压力、饱和度和组分等;f(x,y)为目标函数;n为控制时间步数;Qo,t、Qw,t和Qi,t分别为时间步t对应的产油速度、产水速度和注水速度,m3/d;ro为原油价格,元/m3;rw和ri分别为水处理成本和注水成本,元/m3;b为平均年利率,%;pt为经过的时间,a;c(x)为决策变量约束(如现场操作约束、物理约束等);xl和xu分别为下边界和上边界。

2 算法机制

代理模型方法通过少量样本点构建目标函数的近似模型,从而在计算目标函数值时使用代理模型而不是直接调用油藏数值模拟器。由于代理模型计算目标函数值所需计算代价远小于直接调用油藏数值模拟器计算,因此可以有效提高优化效率。基于代理模型的方法通常建立在具有强大全局搜索能力的进化算法的基础上。本文中采用流行的差分进化算法作为优化求解器。

2.1 差分进化算法

差分进化算法(DE)[23]是一种流行的启发式算法,用于解决全局优化问题,并广泛应用于工程优化问题。经典的DE算法如下:

(1)变异。本文中选择“DE/best/1”作为变异策略,

vi=xbest+Mu(xi1-xi2).

(4)

式中,xbest为目前找到的最优解,即最优的井控参数向量;i1,i2∈[1,NP]为相互不同的随机整数;vi为第i个个体变异向量;Mu为一个通常设置为0.5的比例因子。

(2)交叉。

(5)

式中,Uj(0,1)为从0到1均匀分布的任意数;jrand为确保试验向量ui不重复而随机选择的索引;CR为交叉率。

(3)选择。

(6)

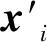
关于差分进化算法的更多介绍可以参阅文献[23]。

2.2 代理模型方法

近年来研究者已经提出了许多近似函数构造代理模型[13-14],如多项式响应面模型[15]、克里金模型[16]、人工神经网络[17]和径向基函数[18]。克里金模型可以从数学角度提供模型的不确定性[12,16,18],因此本文中选择克里金模型作为代理模型。

克里金模型(普通克里金法[24])假定确定性函数为

fp(x)=μ+ε(x).

(7)

式中,μ为样本点的平均常数;ε(x)为具有零均值的自相关误差项,是样本点之间的广义距离的函数。

ε(x)用高斯相关函数作为变差函数的相关结构给出:

(8)

式中,N为x的维数;σ2为设计点的方差;φk为第k维的相关系数。

具体而言,在给定一组Ns数据(x,f)之后,通过最大似然函数估计参数μ、σ和φ[12]。最优无偏估计为

(9)

其中

r(x)=[R(x,x(1)),…,R(x,x(Ns))].

均方误差为

(10)

选择校正个体时个体的目标函数和代理模型的预测精度都很重要。为了平衡这两个因素的影响,已经提出了很多标准,例如预期改进(ExI)[25]、改进概率(PoI)[12]和最低置信区间(LCB)[26]。本文中选择LCB策略。给定预测分布,预筛选的值定义[26]为

(11)

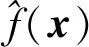
基于LCB动态加点策略的代理模型最小化目标函数过程如图1所示。首先通过试验设计方法取几个样本点作为初始样本点,然后构建代理模型来近似目标函数,根据LCB策略使用差分进化算法筛选出下一步加点的所在位置,逐步动态取样完善代理模型精度,逼近全局最优点。

图1 基于LCB动态加点策略的代理模型优化过程示意图Fig.1 Schematic diagram of surrogate-assisted optimization process based on LCB strategy

2.3 降维方法主成分分析

由于油藏注采优化问题变量多,直接用克里金插值构建的近似模型误差大,难以实现对数值模拟器进行有效的近似。因此采用主成分分析方法对优化问题进行降维处理。主成分分析(PCA)[27]是一种常用的线性降维方法,可以将高维数据转换为低维数据。在克里金代理模型中,输入变量过多不仅会增加代理计算的复杂性,代理模型的精度也会下降,影响优化的效率和精度。因此本文中采用主成分分析方法对数据进行降维。

PCA假设数据之间为线性关系,在保存原始数据的协方差结构的基础上计算低维表达,即最大化总体方差。PCA的目标函数为

(12)

其中

Xi=(xi1,xi2,…,xir),Yi=(yi1,yi2,…,yir).

2.4 SADE-PCA算法优化计算步骤

代理模型的优化过程比传统的进化算法更有效,但当处理油藏注采优化问题时,由于优化变量过多导致参数优化搜索空间巨大,代理模型对油藏数值模拟器的近似能力大大降低。当直接使用基于代理模型的差分进化算法(SADE)进行优化时,由于变量过多,直接采用代理模型进行优化会导致参数优化搜索空间巨大难以构建高精度的代理模型,即少量样本点无法建立足够精度的代理模型。为了利用低维空间中的基于代理模型的优化方法,在建立代理模型之前,利用主成分分析将数据从高维空间转换为低维空间。随后,利用低维数据构建更高精度的克里金代理模型。因此搜索可以集中在由代理模型引导的适应度高的小区域。SADE-PCA算法的流程如图2所示。

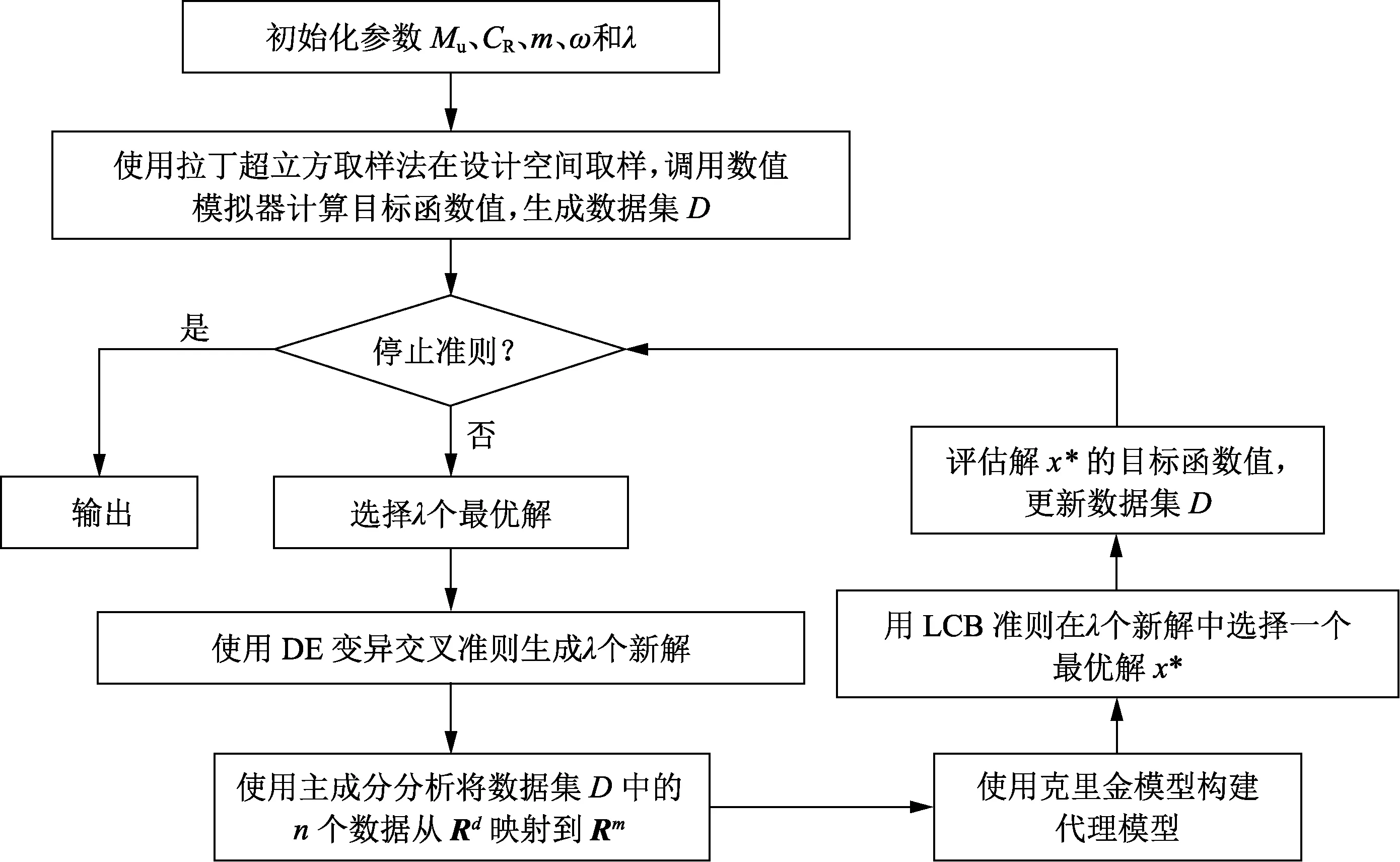
图2 SADE-PCA流程Fig.2 Flow diagram of SADE-PCA

3 计算实例

基于油藏数值模拟软件Eclipse,以油藏实例Egg模型[28]为例,应用SADE-PCA算法进行测试,并与传统进化算法和直接代理优化算法进行比较。Egg模型是一个在水驱生产下的非均质油藏模型,有18 553个有效网格,共有8口注水井和4口生产井。模型渗透率及井位分布如图3所示。模型详细说明见文献[28]。生产井以39.5 MPa的井底压力定压生产。需要优化的控制变量为8口注水井的注水速率。每口井的最大允许注水速度为79.5 m3/d,最小速度为0 m3/d。原油价格为80.0元/m3,注水成本为5.0元/m3,水处理成本为19.0元/m3,平均年利率为0%。

图3 Egg模型渗透率分布Fig.3 Permeability distribution of Egg model

要优化的变量数为注水井数乘以控制步数。一般控制步数越多,优化越有效,即获得更高的净现值。控制步数越多,则具有更大的自由度,优化问题能够实现更高的净现值。然而,控制变量数增多意味着迭代次数增加才能收敛,优化算法需要更多的计算资源才能收敛。Sorek等[29]引入了一种函数控制方法(FCM)和插值控制方法(ICM)以减少计算量,实现适合油田实际应用的平滑注采调控。ICM方法通过选择几个等距插值点作为优化变量以表示沿时间范围的井控变量,其他井控变量通过三次样条插值确定,ICM方法示意图如图4所示。本文中利用插值控制方法缓解由控制时间步数量引起的优化效率和精度的矛盾,减少优化变量数目,并提供平滑的井控方案。Egg模型的总生产周期为3 600 d,模拟生产时间步长设为90 d。因此需要优化的变量总数为8×40=320。选择对每口井用10个插值点进行控制优化,控制变量的数量减少到8×10=80。

图4 插值控制方法示意图Fig.4 Schematic diagram of interpolation control method

为了比较不同方法的结果,分别用SPSA、En-Opt、DE、DE+ICM、SADE+ICM和SADE-PCA+ICM方法对Egg模型进行优化,其中SPSA和En-Opt算法属于近似梯度类算法。由于近似梯度类算法的优化结果极大取决于初始点的选取,对程序进行5次运行,取平均结果。净现值随数值模拟调用次数变化结果如图5所示。在有限的数值模拟调用次数下,近似梯度类方法(SPSA、En-Opt算法)相比差分进化算法表现出明显的优势。DE方法经过800次迭代优化后,从初始的1.867×107元增长到2.267×107元。使用ICM方法后,净现值增长到2.503×107元,相比直接用DE方法优化,提高了10.41%。由于代理模型在变量多的情况下无法实现对油藏数值模拟器进行有效近似,SADE+ICM方法甚至比DE+ICM方法的最终优化结果差。这说明代理模型在优化过程中起到了反作用,代理模型在筛选过程中误导了差分进化算法产生的子解。这是因为代理模型在高维空间中失去了准确性,误差大。使用降维方法后,SADE-PCA+ICM方法与DE+ICM方法相比优化效果改善,说明代理模型在优化过程中对子解的筛选过程促进了优化进程,改善了优化效率。与DE优化结果相比,SADE-PCA+ICM在相同的数值模拟调用次数下优化出的净现值增长到2.720×107元,提高了19.98%。因此从优化结果和优化效率来看,SADE-PCA+ICM方法收敛性最好,能够满足油藏生产优化要求,同时为三次采油油藏开发方案的优化提供了新思路。

图5 各算法的净现值优化结果Fig.5 Optimization result of net present value with different algorithms

各优化方法最终的油藏累积产油量、累积注水量、累积产水量和含水率随时间变化如图6所示。对比几种不同方法优化结果,SADE-PCA+ICM提供的方案有效地降低了油井水的产出量,提高了波及系数,有效改善了油田经济开发效益。各优化方法计算所得的对8口注水井的最终生产调控如图7所示。图7中1控制步为90 d,不使用ICM方法的DE的注水井调控方案如图7(a)所示,其同一口井相邻两控制步的数值相差较大,调控方案不稳定且振荡,不利于现场实施,且注水井注入量变化过大会导致井底压力变化过大,损害储层,导致出砂等现象。利用ICM的优化算法可以提供平滑的生产调控方案。

图6 各算法优化后油藏累积产油量、累积注水量、累积产水量和油田含水率随时间变化Fig.6 Variation of accumulative oil production, water injection, water production and water cut of reservoir with time after different algorithms optimization

图7 各算法注水井调控Fig.7 Water injection well controls for different algorithms

4 结束语

针对油藏注采优化变量多,直接使用代理模型优化结果变差的问题,提出了SADE-PCA方法,通过主成分分析对数据进行降维,而后借助基于代理模型的差分进化算法进行优化,最终得到实际生产优化问题的调控方案。应用SADE-PCA方法对Egg模型进行了实例计算。优化所得的最优调控方案通过对生产制度进行调控,有效地降低了油井水的产出量,增大了原油产量,提高了油田经济开发效益,进一步验证了方法的有效性。插值控制方法(ICM)在实现平滑的调控方案和提高计算效率方面具有良好性能。使用ICM方法后,代理模型结合主成分分析的方法可以更有效地解决实际油藏注采优化问题。