汽车滑动门外偏量模型研究

周福荣 刘晶

【摘 要】文章对滑动门外偏量进行模型简化，通过简化模型得出不同位置外偏量与导轨分布的数学关系，根据得出的数学关系指导滑动门前期设计;定义了滑动门车门姿态，通过简化模型量化了车门姿态的评估方法，可用于分析和指导实际生产中车门姿态的调整。

【关键词】汽车;滑动门;外偏量

【中图分类号】U463.834 【文献标识码】A 【文章编号】1674-0688（2020）03-0044-02

0 前言

滑动门作为汽车常用的侧门类型，普遍应用在微型商用车、商务MPV，滑动门约束条件的特殊性决定了开启的平顺性，成为评估车门性能的重要指标[1]，而与平顺性关联的外偏量则是评估车门的直观数据，因此研究滑动门外偏量及其简化模型，在设计和实际生产中有着重要的指导意义。

1 滑动门系统相关定义

1.1 汽车滑动门的定义

汽车滑动门是通过上走轮臂、中走轮臂和下走轮臂分别在上导轨、中导轨和下导轨沿着固定轨迹移动的车门[2]。

1.2 最小外偏量的定义

能够保证滑动门正常打开的最小Y向车门位移，用D表示，该位移量与3个因素有关，分别是门厚度A，运动安全距离B、门上附件Y向高度H，其关系如下：

D=A+B+H（1）

1.3 滑动门运动模型的基本形式

简化的滑动门运动模型有两种：第一种是上、中、下导轨处车门的外偏量相同，该种模型是理想的运动模型，能够保证车门打开时车门上所有部件不存在相对移动，即车门完全平移打开。第二种是上、中、下导轨处车门的外偏量不同，外偏量由上到下逐渐增加，该种模型是实车普遍采用的模型，在车门打开时，车门会在X-Z平面小角度倾斜后再进行平移[3]。

1.4 滑动门车门姿态

因为上、中、下导轨处车门外偏量不同，所以车门打开后在X-Z面上呈现小角度的倾斜，此时车门X方向的不同位置外偏量也会有差异，主要体现在滑动门前上角与后上角Y向差异，前下角和后下角Y向差异，以上差异在评估滑动门开启状态时称之为车门姿态。

2 滑动门不同位置外偏量关系

一般确定滑动门最小外偏量的区域在中导轨位置，主要影响部件为摇窗机手柄或扶手台，以上零件在车门正常打开时的最小Y向位移确定为该车的最小外偏量。为保证侧围冲压要求和走轮臂的垂直刚度要求，一般在设计时会尽量压缩该处尺寸，即保证该处冲压和刚度要求的前提下使该处外偏量实现最大化，该处最小外偏量用D1表示。

上导轨位置的外偏量主要受车身内头部空间和导轨支撑件的冲压要求决定，其中头部空间要求是决定性因素，增大该处外偏量会直接压缩乘员头部空间，进而不满足总布置要求。此外，考虑到冲压板材拉延成型的实际情况，应适当减小外偏量。对于上导轨位置的外偏量一般按照平台化处理，即一个平台采用一个定值进行设计，可以更好地规避设计风险。该处最小外偏量用D2表示。

下导轨位置的外偏量主要由车身大梁Y向布置和车门下部扭转要求决定，车身的承载性要求是车辆设计的重点，下导轨的布置需要在不影响大梁布置的前提下进行，因此下导轨前端应在Y向尽量靠近大梁，满足导轨支架焊接操作空间及安全距离即可;此外，下导轨直线段的-Y向应尽量向滑动门内板靠近，保证滑动门下部扭转刚度满足要求即可。该处最小外偏量用D3表示。

在Z方向上，上导轨的布置受滑动门分缝和门洞影响;中导轨布置主要受造型影响;下导轨的布置受地板和滑动门下部门洞影响;上导轨到中导轨的Z方向距离用L1表示;中导轨到下导轨的Z方向距离用L2表示。

车门外偏量、导轨分布数模及简化模型Ⅰ如图1所示。

模型Ⅰ中外偏量和导轨分布的关系如下：

（D1-D2）/（D3-D2）=L1/（L1+L2））（2）

假设上走轮臂处外偏量D2不变，如果中导轨处车门外偏量增加Δ，下导轨处外偏量增加值X，由公式（2）可得出：

X=（L1+L2）Δ/L1（3）

通过模型简化得出公式（3），可以看出中走轮臂位置增加外偏量与下走轮臂处外偏量为正相关，且增加量只与上、中、下导轨的分布相关。

3 调整外偏量对车门姿态的影响

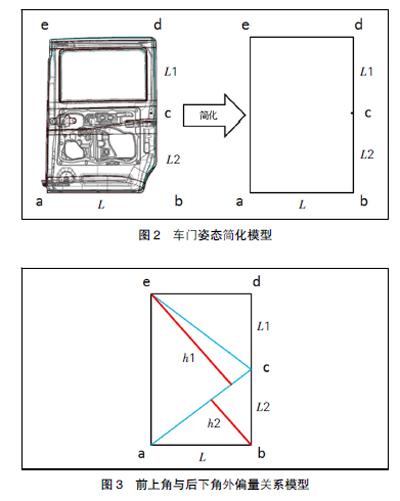
在实际设计过程中，Y向可调整的走轮臂主要是上走轮臂和下走轮臂，中走轮臂外偏量一般不可调整，以下分析调整上、下导轨外偏量对车门姿态的影响。车门简化模型Ⅱ如图2所示，其中上、中、下走轮臂位置分别为e、c和a，门宽为L，上导轨到中导轨的Z方向距离用L1表示;中导轨到下导轨的Z方向距离用L2表示，其中e、a、d和b又分别称为滑动门前上角、前下角、后上角和后下角。

分析上走轮臂处外偏量对车门姿态的影响，调整上走轮臂外偏量，且中走轮臂和下走轮臂均按照固定形式，即调整上走轮臂时，前上角e会绕着ac连线以e到ac的垂线h1为半径进行转动;同时，后下角b会以ac连线以b到ac的垂线h2为半径进行反向转动;当调整上走轮臂e处外偏量Δ时，后下角外偏量y与Δ的关系如图3所示。

y=（h2/h1）Δ

其中，

h1=（L1+L2 L/■;h2=L2 L/■

y=L2Δ/（L1+L2）（4）

同样，可采用相同模型评估下走轮臂外偏量对车门姿态的影响，当调整下走轮臂a处外偏量Δ时，后上角外偏量y与Δ的关系如下：

y=L1Δ/（L1+L2）（5）

通过模型简化得出公式（4）和公式（5），可以看出上走轮臂位置外偏量与后下角外偏量为正相关，下走轮臂位置外偏量与后上角外偏量呈负相关;且变化量只与上、中、下导轨的分布相关。

4 总结

简化的滑动门外偏量模型Ⅰ在车门子系统设计前期可以快速得出下导轨位置外偏量具体数值，能够更直接地评估工程和造型可行性，减少工程和造型反复，缩短产品开发周期;简化的滑动门外偏量模型Ⅱ定义了滑动门车门姿态，量化了车门姿态的工程描述;此外，该模型可用于指导实际生产中滑動门调整，使实际操作有准确的理论依据。

参 考 文 献

[1]滕平，刘晶.基于UG的滑动式车门运动轨迹平顺性分析方法[J].企业科技与发展，2018（10）：92-93.

[2]周福荣，施华滩，韦逢义，等.滑动门上走轮臂与上导轨干涉问题研究[J].企业科技与发展，2015（3）：24-26.

[3]刘鹏飞.汽车滑移门系统的运动学和多刚体动力学建模与参数优化[D].上海：上海交通大学，2013.