超载现象对连续梁桥跨中截面的影响

吴隆　李海涛

摘要：为满足经济需求采用的卡车超载货物运输现象已屡见不鲜，以此现象分析了卡车在超载情况下对连续梁桥跨中部位的影响。采用有限元方法对桥梁及3种不同类型卡车进行模拟，得到桥梁的自振频率及跨中位移值，同时通过数值计算的方法对数值模拟进行了检验。结果表明：随着卡车荷载的增加，其自身振动频率随着模态的上升而下降，对桥梁跨中的位移值成上升的趋势，最终可能会导致桥梁与卡车造成共振现象，同时对跨中部位造成严重的变形损伤。通过研究，桥梁在役时要严格控制过往车辆的数量及质量，并且变截面连续梁桥在设计时跨中截面刚度可适当增加。

关键词：卡车荷载;连续梁桥;超载;振动

中图分类号：U448.2文献标志码：A

Abstract： To meet the economic needs， truck overloading is common. Therefore， the effect of truck overloading on the mid-span section of continuous girder bridge was analyzed in this paper. The finite element method was used to simulate the bridge and three trucks with different loading conditions， and the natural frequencies and mid-span displacements values of the bridge were obtained. At the same time， the numerical simulation was verified by numerical calculation method. The results show that with the increase of truck load， its own vibration frequency decreases with the increase of modal， and the displacement value of the bridge mid-span position becomes an upword trend， which may eventually lead to the resonance between the bridge and the truck， and cause serious deformation damage in the middle part of the span. Through research， the number and quality of vehicles should be strictly controlled during the service of the bridge， and the stiffness of mid-span section of variable cross-section continuous girder bridge can be increased appropriately in design.

Keywords：

truck load;continuous girder bridge;overload;vibration

隨着桥梁工程理论的不断完善及有限元技术的不断精进，众多桥梁方面的专家及学者对桥梁在受到不同荷载作用下的动静力响应作出了不同方面的研究。徐行军等[1]对预应力混凝土连续梁桥进行了振动测试，分析其动力响应;蒲军平等[2]针对多跨变截面连续梁桥在车辆通过时的耦合振动问题通过移动质量模型对其进行动力响应分析。施颖等[3]将车辆和复杂桥梁视作2个分离子体系，通过广义虚功原理、有限元法、位移协调方程及车桥相互作用方程建立起车桥耦合振动方程，分析了复杂桥梁的车桥耦合现象。朱志辉等[4]将列车等效成31自由度刚体动力模型，研究了列车-大跨度板桁结构斜拉桥耦合振动引起的整体与局部振动相应问题。

由于各种大型运输货车的出现，并且为了降低运输成本，往往都是超载运输，这使得桥梁使用寿命大大减小。赵少杰等[5]通过动态称重系统（WIM）并结合人工调查，显示如今桥梁超载现象十分频繁，且超载超限现象中更多的车辆是大型卡车。Tabatabai等[6]通过WIM技术为卡车进行分类并进行为期1年的数据收集和分析，结果表明5轴卡车（定义为9级卡车，下同）1年中的通行量占全部卡车的61.72%。目前桥梁的承载能力大小都是根据设计规范进行荷载试验评定的，梁栋等[7]提出以桥梁实际工作下的荷载等级为标准，选用跑车试验，利用动挠度作为评价指标来评定桥梁的承载能力。但是对车辆超载情况对桥梁跨中截面会造成如何的影响现有文献中涉及不多，本文通过对比3轴卡车[8]（定义为标准卡车，下同），9级卡车及超载的9级卡车以桥梁的最大设计速度通过一变截面连续梁桥，运用有限元软件进行模拟，并通过数值计算的方法进行检验，分析各类型卡车对桥梁跨中的动力作用。

1 有限元分析

1.1 桥梁模型的建立

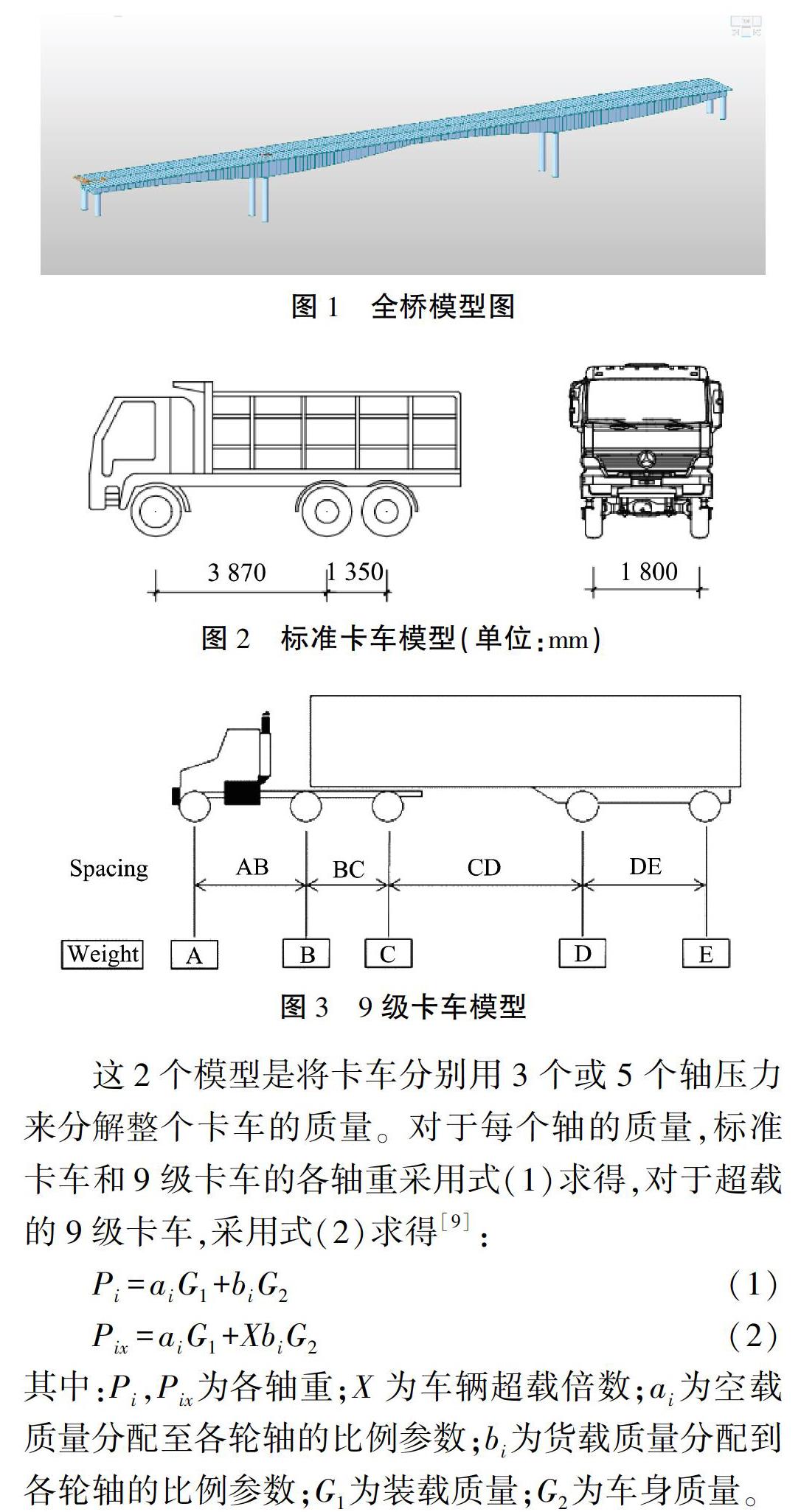
本文对汶川地震后重建的45 m+76 m+45 m变截面连续梁桥以1 m为单元特征尺度建立全桥有限元模型如图1所示。其中，桥面铺装，防护栏等作为二期恒载作用在桥面上。

1.2 车辆模型的选择及模型分析

选用桥梁荷载试验所采用的标准卡车（见图2）

及9级卡车（见图3）作为模拟所采用的车辆荷载。

建立3车道，并让车道达到满载状况并以设计时速加载进行动力分析。得到桥梁自振的前3振型如图4所示，并得到其前3自振周期如表1所示，在施加3种卡车荷载作用后的跨中变形图如图5所示，及3种荷载情况下桥梁最大跨中变形值见表2。

从位移图及表可以看出随着卡车载重的增加，跨中部分的位移值也不断增加，这可能会对跨中部分造成损伤。

2 数值计算验证

对于车辆模型的简化，陈上有等[10]用车轮加弹簧-阻尼器-簧上质量体系来模拟车辆，但这种模型忽略了车轮与地面之间的相互作用，得到的结果可能会有一定的偏差，故本文采用了多个轴重，弹簧，阻尼连接多个刚体所得到的三维车辆模型[8]，图6所示为标准车辆的三维模型。

其中：标准车辆质量矩阵M由车辆的总质量、转动惯量、轴重构成10×10的对角矩阵，9级卡车为16×16的对角矩阵;K为刚度矩阵，其中各值可由Lagrange方程求得[7];C为阻尼矩阵，其数值可根据已有试验得到相关数值[11]并通过Lagrange方程求得。由于本文已假设所有卡车以设计时速运行，故已知其起始速度及初始位移，可采用经典阻尼体系对其进行求解。

经过计算，可以得到3种车辆荷载的前3振型频率如表3所示，3种卡车振动的前3振型图像，如图7所示。

与数值模拟所得到的结果对比可以发现，卡车对跨中作用的位移值相差不大，即模拟结果与真实情况相差不大。

同时通过图7和表3可以发现，随着荷载重量的增加，卡车前3振型频率不断降低，不断地接近桥梁的自振频率，很可能会和桥梁本身的频率达到相同，即发生共振，造成重大损失。同时随着质量的增加，卡车对跨中作用的位移值也不断增大，对桥梁造成更大的损害。

3 结论

本文通过对卡车超载情况下连续梁桥动力特性进行了数值模拟及理论验证，通过对比二者的结果可以发现：

1）通过对3种不同的卡车荷载及桥梁进行模拟，并构造时程函数进行分析，最终得到桥梁的自振频率、跨中位移、卡车荷载的振动频率及振幅，并通过数值计算进行检验，发现计算结果与模拟结果較吻合，故在今后分析中可直接运用数值模拟方法进行工况分析。

2）随着车辆荷载的增加，车辆自振频率随着质量的上升而变小，当严重超载时可能会发生共振现象，造成严重的经济损失。

3）随着车辆荷载的增加，桥梁跨中位移值不断增大，且在第1振型下尤为明显，随着时间的推移会大大损伤桥梁。由于变截面连续梁桥在跨中部分截面面积较小，故在设计时跨中截面的刚度可适当增加。

参考文献：

[1]徐行军，卓维松.预应力混凝土连续梁桥振动测试与动力特性分析[J].成都工业学院学报，2019，22（1）：28-31，44.

[2]蒲军平，汪小超，刘鹏.多跨变截面连续梁桥在车辆通过时的振动分析[J].中国公路学报，2009，22（1）：66-71.

[3]施颖，宋一凡，孙慧，等.基于ANSYS的公路复杂桥梁车桥耦合动力分析方法[J].天津大学学报，2010，43（6）：537-543.

[4] 朱志辉，徐智伟，程玉莹，等.基于精细有限元法的车致大跨度斜拉桥整体及局部振动研究[J].湖南大学学报（自然科学版），2018，45（1）：9-18.

[5]赵少杰，任伟新.超限超载交通对桥梁疲劳损伤及可靠度的影响[J].中南大学学报（自然科学版），2017，48（11）：3044-3050.

[6]TABATABAI H，TITI H，ZHAO J.WIM-based assessment of load effects on bridges due to various classes of heavy trucks[J]. Engineering Structures，2017（140）： 189-198.

[7]梁栋，董婉，杜延昭，等.基于实际车流的在役桥梁承载力动态评定方法[J].土木工程与管理学报，2018，35（1）：21-27.

[8]LI Y， CAI C S， LIU Y，et al. Dynamic analysis of a large span specially shaped hybrid girder bridge with concrete-filled steel tube arches[J].Engineering Structures， 2016（106）： 243-260.

[9]刘扬，张海萍，邓扬，等.考虑车辆超载的公路简支梁桥疲劳性能[J].浙江大学学报（工学版），2015，49（11）：2172-2178.

[10] [10]陈上有，夏禾，战家旺，等.变速移动荷载作用下简支梁的动力响应分析[J].中国铁道科学，2007（6）：41-46.

[11] [11]CHOPRA A K.结构动力学理论及其在地震工程中的应用[M].谢礼立，吕大刚，译.2版.北京：高等教育出版社，2005：334-347.