基于拉格朗日方程组的铰接工程车辆稳定性分析

张浩辰　线晨

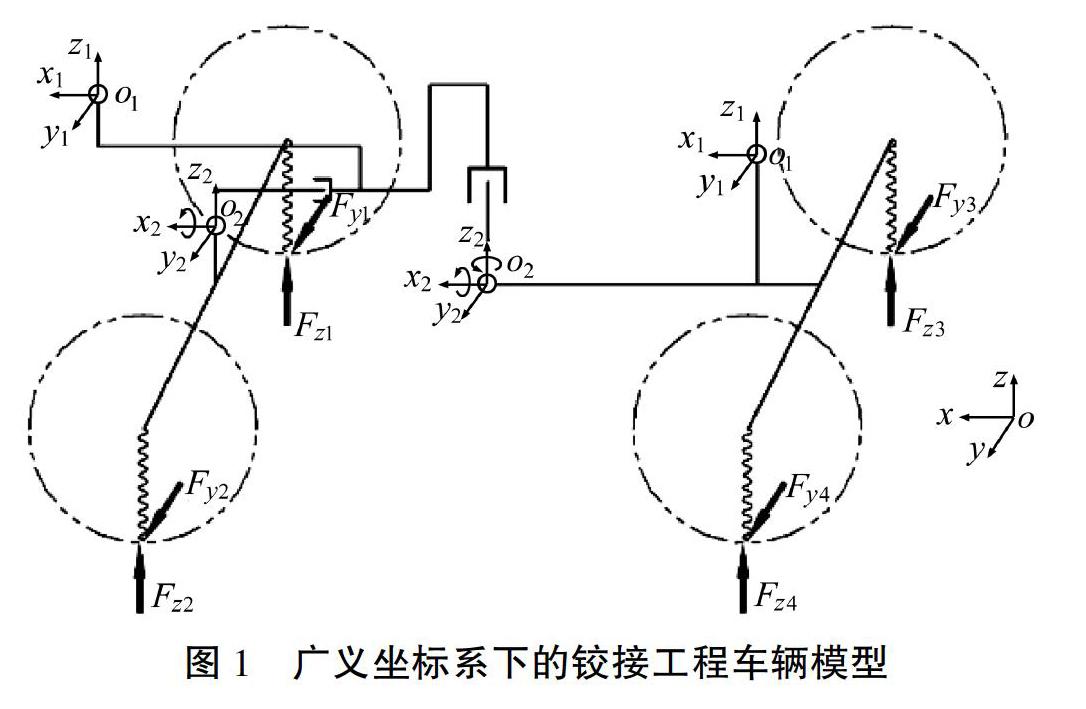
摘要：为分析铰接工程车辆在行驶过程中的稳定性，找出影响铰接工程车辆的稳定性的主要因素和影响权重。建立了斜坡路面的工作空间变量作为系统广义坐标，根据前置摆动桥的铰接结构，得到与广义坐标相对应的5自由度拉格朗日动力学方程-运动微分方程。结合Fiala轮胎模型和虚功法，采用可变步长BDF算法解出铰接工程车辆横向载荷转移率（LTR）变化规律，并以此规律作为该车型侧倾稳定性的评判标准判别该车型稳定性。采用正交试验方法，选取转向行驶速度、转向角速度、横向坡度角为主要因素，设计正交试验分析该型国产铰接工程车辆LTR曲线变化规律。通过对极差结果的分析找到了影响该车型侧倾稳定性的主次因素排序。

关键词：铰接工程车辆;广义坐标系;拉格朗日方程组;侧倾稳定性;LTR评价

中图分类号：TH113文献标志码：A

文章编号：2095-5383（2020）02-0043-05

Abstract： In order to analyze the driving stability of articulated vehicles， the main factors and weights that affect the stability of the articulated vehicles were find out. The workspace variables of the slope pavement were established as the generalized coordinates of the system.  5 DOF Lagrange dynamics equations-motion differential equations corresponding to the generalized coordinates were established according to the articulated structure of front swing bridge. Combining the Fiala tire model and virtual work method， the variable step BDF algorithm was used to solve the change law of the lateral load transfer rate （LTR） of articulated vehicles， and this law was used as the judging standard for the roll stability of the vehicle. The orthogonal testing method was adopted. Selecting the steering speed， steering angle speed， and lateral slope angle as the main factors， the orthogonal test was designed to analyze the change law of the LTR curve of this type of domestic articulated vehicle.The sequence of primary and secondary factors affecting the roll stability of the model were found through the analysis of the range results.

Keywords：

articulated vehicles; generalized coordinates; lagrange dynamics equations;roll stability; Lateral Load Transfer Ratio

工程車辆作为野外施工的主要工具，由于其具有良好的环保性、高效性、安全性，所以得到了广泛的应用，尤其是油气资源勘探领域。与此同时，工程车辆在实际工作中面临许多不可预料的恶劣路况问题[1]。铰接型工程车辆比直连型工程车辆的最小转向半径更小，转向半径范围更大，转向时更容易避让障碍物，纵向通过半径加大。同时横向稳定性较弱，且前驱动轮没有定位角，在侧向容易发生失稳。但由于油气勘察一般比较偏远，一旦车辆发生事故，很难得到及时救援，不仅影响勘探效率，甚至威胁到驾驶人员的生命安全。因此开展有关铰接工程车辆稳定性分析以提高物探工作效率和保证人员的安全是十分必要的。

近年来，国内外学者做了很多道路车辆的侧倾稳定性研究，也有部分学者将其研究成果应用于非道路车辆防倾翻技术的改进。但是由于铰接工程车辆和公路车辆在工作环境、车身结构、侧倾稳定机理等方面差异较大，其侧倾稳定性理论和防翻技术均不同于道路车辆，因此需要重新建立适合铰接工程车辆动力学模型，求解广义坐标系下的广义力。姚宗伟等[2-4]利用广义坐标形式下的拉格朗日方程组分析了关铰接式半挂车和装载机的侧倾稳定性，并取得了一定的成果。Yao等[5]较全面地建立了多因素的状况下铰接车辆的运动模型，研究了在平地转向时不同要素在转动过程中的控制算法，其计算过程复杂，且计算量庞大，不易在工程领域直接应用。因此，本文针对铰接工程车辆建立了5自由度的拉格朗日方程组，全面考虑不同因素对于整车稳定性的影响，分析了铰接工程车辆侧倾稳定性的变化规律。为设计局部坐标系下的主动防翻机构和预警系统提供参考依据。

1 铰接工程车辆侧倾稳定性评价指标

车辆行驶稳定性评价一般由速度、加速度、转向速度等运动参数确定。由于铰接工程车辆工作时行驶速度较低、整车质量较大、加速度变化不明显，因此不宜作为评价侧倾稳定性评价标准。本文采用横向载荷转移率（Lateral Load Transfer Ratio，LTR）作为铰接工程车辆侧翻危险性的评价指标[2]，可以有效反映整车在运动过程中侧倾稳定性的变化情况，定义为左右两侧轮胎上垂直载荷之差与轮胎垂直总载荷比值的绝对值：

2 铰接工程车辆动力学模型建立

2.1 基本假设

根据现场实际情况以及受力状况建立模型，基本假设如下：1）假定前、后车、摆动桥均为刚体在模型建立时作为质点考虑。2）假定铰接工程车辆上所有的局部坐标系，固连在前后车体及摆动后桥的质心处且符合右手系;3）假定铰接式工程车辆匀速行驶，即牵引力等于摩擦力;4）本次分析不考虑铰接式工程车辆的俯仰运动;5）假定所有轮胎的物理性质相同。

据本节2.1假设，本文只考虑以下运动：1）沿工程车辆前进行驶方向的纵向运动;2）沿前进方向的左侧的横向运动;3）沿地面向上的垂直运动;4）绕z轴的横摆运动;5）绕x轴的侧倾运动。同时，各局部坐标系的运动并不是独立的。其中可做统一考虑的有：前车体、后车体及摆动后桥沿x轴的纵向运动、沿y轴的横向运动、沿z轴的垂直运动以及绕z轴的横摆运动。铰接工程车辆采用前桥摆动，摆动角度在限位块的作用下限制在±15° 之内。因此，摆动前桥相对于前车体和后车体具有独立的侧倾运动，侧倾角设为θ1。此外，根据模型假设3），假设工程车辆行驶速度恒定，则其沿x轴的纵向自由度便可不予考虑。最终，铰接工程车辆只剩下1个沿y轴的横向运动，横向位移为y;1个绕z轴的横摆运动，横摆角为

;2个侧倾运动，即前后车体绕x轴的侧倾运动，侧倾角为θ，以及摆动后桥绕x轴的侧倾运动，侧倾角设为θ1，共5个自由度。

从表3可知，每一列LTR的均值和方差的极差均不相同，该因素在水平变化对指标影响的大小程度是由极差反映的，一般来说：极差越大，铰接震源车稳定性被在该因素下所选的水平数影响越大。因此，可以直观得看出对指标影响最大的因素，即最主要因素。分析可知，对铰接震源车的稳定性造成影响主要是LTR值的大小及LTR曲线的波动，其通过均值影响稳定性的主次顺序为φ，·，x·;通过方差影响稳定性波动的主次顺序为φ，x·，·。

5 结论

LTR曲线在不同因素作用下的计算结果呈非线性变化，说明该型铰接工程车辆侧倾稳定性在斜坡转向时呈现一定的波动;LTR较高的区域和LTR曲线波动明显的区域都会导致工程车辆失稳。

以x·、·、φ为主要因素，利用正交试验法和极差分析法分析3因素水平变化是对铰接震源车稳定性的影响均不相同，其主次順序为φ、·、x·。

参考文献：

[1]刘航.可控震源车侧翻保护结构安全保护性能评价与改进[D].成都：西南石油大学，2015.

[2]姚宗伟.铰接转向工程车辆侧倾稳定性研究[D].长春：吉林大学，2013.

[3]曲俊娜.铰接式工程车辆动态侧翻稳定性研究[D]. 长春：吉林大学，2013.

[4]YU H， GVENC， LEVENT. Heavy-duty vehicle rollover detection and active roll control[J]. Ifac Proceedings Volumes， 2005， 38（1）：128-133.

[5] YAO Z， WANG G， LI X， et al. Dynamic simulation for the rollover stability performances of articulated vehicles[J]. Proceedings of the Institution of Mechanical Engineers Part D Journal of Automobile Engineering， 2014， 228（7）：771-783.

[6]高征，苏锐.广义坐标的选择在Lagrange动力学分析中的作用[J].机械设计与制造，2010（11）：54-56.

[7]

SOLMAZ S， CORLESS M， SHORTEN R. A methodology for thedesign of robust rollover prevention controllers for automotive vehicles with active steering[J]. International Journal of Control， 2007，80（11）：1763-1779.

[8]刘隆， 谢伟平. 含多余广义坐标的拉格朗日方程及实例应用[J].力学与实践， 2013， 35（3）：87-89.

[9]马晓.不同轮胎模型对重型载货汽车整车性能仿真的影响分析[D].长春：吉林大学，2013.

[10]齐朝晖.多体系统动力学[M].北京：科学出版社， 2008.

[11]陈立群.理论力学 [M].北京：清华大学出版社， 2006.