机载风能系统动力学建模
沈婉慧子


摘 要:机载风能(AWE)具有发电成本低、发电效率高、环保等优势,对机载风能系统(AWES)及其发电技术的研究在高空风能利用领域具有重要的意义。为了使机载风能系统可靠且持久地运行,系统建模以及在发电过程中控制系绳翼飞行是本领域的关键问题。AWES是动力学和空气动力学相互作用的产物,对AWES动力学的建模是设计的基础,需要从简单的模型开始。因此文章提出了一个简单的机载风能系统动力学模型。
关键词:机载风能系统;动力学建模;风筝发电
中图分类号:S229 文献标志码:A 文章编号:2095-2945(2020)20-0040-02
Abstract: Airborne wind energy (AWE) has the advantages of low power generation cost, high power generation efficiency, environmental protection, etc. The research of airborne wind energy system (AWES) and its power generation technology is of great significance in the field of high altitude wind energy utilization. In order for the airborne wind energy system to operate reliably and lastingly, system modeling and controlling tether wing flight during power generation are key issues in the field. AWES is the product of the interaction between dynamics and aerodynamics. Modeling AWES dynamics is the foundation of the design, which needs to start with a simple model. Therefore, this paper presents a simple dynamic model of airborne wind energy system.
Keywords: airborne wind energy system; dynamic modeling; kite power generation
引言
自八十年代初以来,研究界注意到在距离地面200米至10公里范围内的高空风具有更强更持久的能量[1]。由此,出现了一个全新的可再生能源领域-机载风能(AWE),AWE的目标是在距离地面较远的高空中捕获风能,获得这种风能的机器可以称为机载风能系统(AWES)[2]。根据所采用飞行器机翼的类型,AWES可分为柔性翼风筝、刚性无人机翼。由于柔性翼风筝更安全且更容易操作,成本也比较低,因此本文选择对柔性翼风筝系统进行研究。在过去的几年中,出现了一些描述柔性翼风筝系统的模型用于开发和测试[3-5]。
AWES的能量转换通过两个阶段的运动循环实现,该循环由一个产生电能的发电阶段和一个消耗较少能量的回收阶段组成。系统中,牵引风筝的绳索缠绕在绞车上,而绞车又连接到电动发电机的轴上。在发电阶段,风驱动飞机产生升力,在绳索上产生牵引力,从而带动发电机的旋转。在发电阶段最常用的飞行模式是具有圆形或八字形路径的侧风飞行。在回收阶段,电动机将绳索收回,使飞机回到原来的位置。为了达到正平衡,通过控制系统调整飞机的气动特性[6]或控制其飞行路径[7]使得在发电阶段产生的能量最大化以及在回收阶段消耗的能量最小化。AWES是动力学和空气动力学相互作用的产物,对AWES动力学的建模是设计的基础,需要从简单的模型开始。因此本文对AWES在发电过程中的运动进行动力学建模。
1 坐标设置与约束
为了分析风筝的运动,建立两个坐标系。首先建立球坐标系:定义ex为风向,ez指向重力方向,ey与ex、ez平面垂直。坐标系中任意的风筝位置由球面坐标中的参数r以及两个方位角(系绳在ez、ey平面投影与ez的夹角)和 (绳索与ex的夹角)给出。另一个坐标系为建立在风筝翼面上的非惯性坐标系(eroll、epitch和eyaw),eroll(滚动轴,与仰角相关,系绳与ez、ey平面夹角),epitch(俯仰轴,与相关)和eyaw(偏航轴,与系绳方向一致)。
在所建立的球坐标中,风筝状态由三个自由度决定:风筝位置r(ex,ey,ez)与方位角的对应关系为
如忽略重力,风筝的受力、运动状态与无关。令=0,可得到特定情况下基础向量的表达式为
为描述风筝的运动,对风筝模型需要满足的条件进行限定:
(1)AWE系統所受空气动力要比其本身质量大。这是风筝飞行的先决条件,并满足常规操作模式。简化风筝运动,不考虑工作过程中的加速行为。
(2)假设系绳是无质量的刚性杆。这种假定是因为张力远大于系绳重力。
(3)假设风筝任一瞬时始终处于空气动力学的平衡状态。该假设是为了便于分析风筝受力后的运动情况,假定的空气动力平衡并不意味着风筝不运动。
(4)假设沿轴具有速度的恒定且均匀的风场。
2 运动方程描述
风筝的基本运动为恒定线长情况下的运动。此时,风筝翼面的表面风速va(图1中)可推导为
该式的后两个部分描述了风筝运动速度vroll和vpitch在非惯性坐标系中eroll和epitch上的投影。风筝翼面的表面风速矢量始终位于eroll-epitch平面,因此而且,表面风速va在eroll、eyaw上投影的比值即为滑翔比E,E原本定义为升力和阻力系数之间的比率
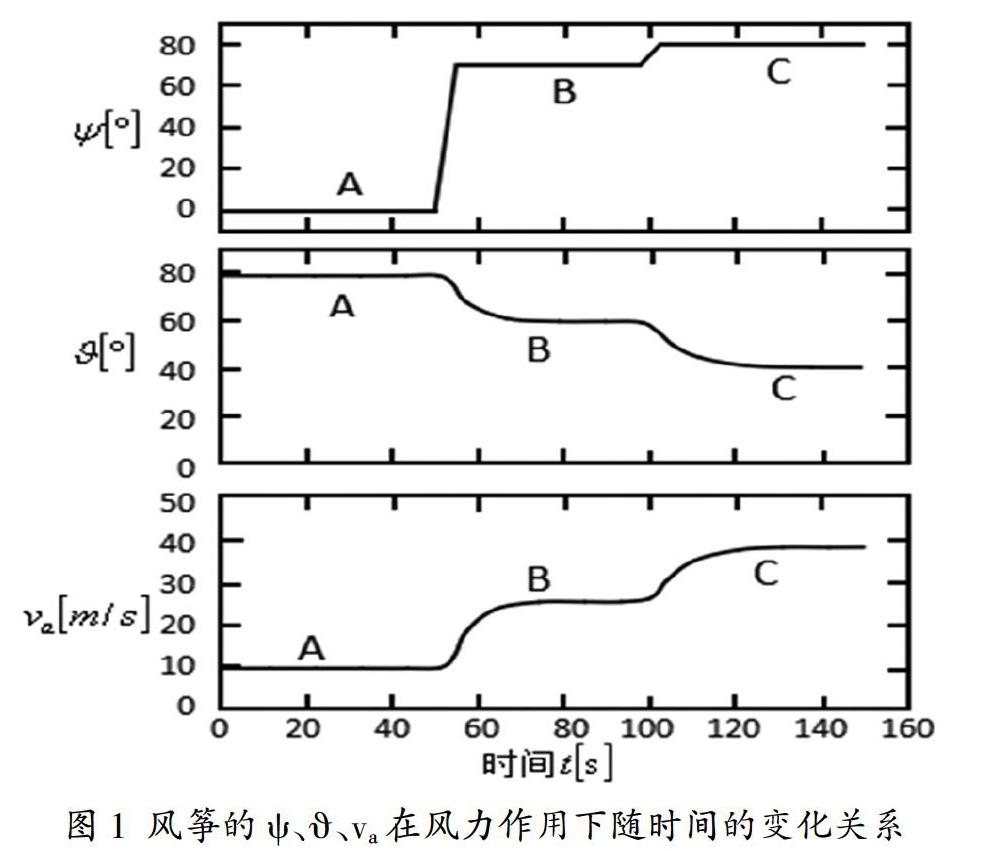
考虑基本的风筝运动方程,假设系绳l=100m,风速zvw=10m/s,升阻系数E=5,ex为风向,不考虑风筝和系绳的重量,风筝的运行只受气动力和系绳接力的作用,在圆形轨道上飞行。风筝从位置A开始在风力的作用下运动,在风力与拉力的共同作用下角度逐渐增加,由于系绳长度固定,风筝将会“下降”,围绕ex旋转的直径开始变小同时达到一定的表面速度va,进入圆轨道B上运行。一段时间后,风筝的角度?鬃进一步增加,到直径更小、速度更快的轨道C上运行。
3 仿真分析
对上述风筝运动方程进行仿真,图1中分别为风筝的、va在风力作用下随时间的变化关系,为70°左右时形成圆形轨道B,?鬃为83°左右时,形成圆形轨道C。并且随着的增加,圓的直径和?谆减小,表面风速va增加。
风筝在A点时,=90,假定的瞬时状态为稳态,所以风筝在该角度方向上不会有变化,所以带来的初始条件=0,可得
表面风速va可由角度确定,系线张力与v成比例,当值固定时将导致出现极值0,综上所述,值可以用于控制系线张力。实际上,在放风筝的实践中已经感知到了这一理论,根据风筝在风窗中的位置即,通过系绳控制牵引力,放飞风筝。
4 结束语
本文提出了一个简单的机载风能系统动力学模型,并通过仿真分析得出风筝翼面的仰角可控制系线张力。柔性翼风筝发电是系绳周期性变化的运动,系绳长度会发生变化,因此之后将在本文恒线长模型的基础上进行扩展,通过引入卷筒扩展模型,使模型更适用。
参考文献:
[1]I.Bastigkeit,Study on wind resources at mid-altitude[J].Abstract submitted to the Airborne Wind Energy Conference,TU Delft;2015.
[2]Cherubini A,Papini A,Vertechy R,et al.Airborne Wind Energy Systems: A review of the technologies[J].Renewable and Sustainable Energy Reviews,2015,51:1461-1476.
[3]Fagiano, L.: Control of tethered airfoils for high-altitude wind energy generation. Ph. D. Thesis, Politecnico di Torino,2009.
[4]Houska, Boris, Diehl, Moritz.Robustness and stability optimization of power generating kite systems in a periodic pumping mode[J].2010.
[5]Williams P, Lansdorp B, Ockesl W. Optimal Crosswind Towing and Power Generation with Tethered Kites[J].Journal of Guidance Control & Dynamics, 2008, 31(1):81-93.
[6]Williams P,Lansdorp B,Ockels WJ.Optimal crosswind towing and power generation with tethered kites[J].Guid Control Dyn,2008,31:81-93.
[7]Canale M, Fagiano L, Milanese M. KiteGen: a revolution in wind energy generation[J].Energy,2009,34:355-61.

