数学活动经验结构化的教学价值与实施
章婷?

【摘要】数学活动经验结构化是建立完整的数学知识体系的前提,有利于学生思维能力的发展和数 学素 养的 提升 。要促 进学 生的 数学 活动 经验 结构 化,需要 教师 构建 知识 网络 ,让经 验从“零 散”走向“系 统”;挖掘 内涵 关联 ,让经 验从“个 体”走向“整 体”;提升 多元 素养 ,让经 验从“单 一”走向“全 面”。
【关 键词 】数学 活动 经验 ;结构 化;知识 网络 ;内涵 关联 ;多元 素养
数学活动经验是学生在亲身经历数学实践、数学思考、问题解决等数学活动的过程中获得的关于数学知识的意义、数学知识之间的逻辑关系、数学技能、数学思想方法、数学问题解决等方面的感悟。获得基本活动经验是学生数学学习的重要目标之一,对他们获得基础知识、习得基本技能、感悟基本思想具有十分重要的意义。数学是一门结构性很强的学科,不仅有逻辑清晰的知识结构,还有科学系统的方法结构。着眼于学科整体、知识间的联系和学生思维的发展,让学生的数学活动经验结构化,有助于发挥数学活动的价值,能有效提升学生的数学素养。
一、数学活动经验结构化的内涵和实践价值
(一)数学活动经验结构化的内涵
所谓数学活动经验结构化,即立足数学教材的知识结构和编排体系,从学生已有的知识经验 和生 活经 验出 发,站在 整体 、系统 、结构 的高度把握、处理教材,沟通知识之间的联系,悉心设计教学方案,精心组织教学活动,引导学生在学习过程中收获系统、整体而全面的知识、技能、体验和感悟。
(二)数学活动经验结构化的实践价值
1.从生活到数学,助推学生形成完整的知识体系。
数学活动经验结构化着眼于数学学科知识的整体建构,注重引导学生通过新知的探究活动,了解学习内容内部各要素之间的关系,明晰所学内容与同单元其他课时内容、同领域其他单元内容、数学内其他领域内容及数学外其他领域内容间的联系,从而不断丰盈学习内容的深刻内涵和丰富外延,构建完整的数学知识体系。
2.从具象到抽象,助力学生思维能力的发展。发展数学思维是数学学习的第一要义,数学认知结构的发展、数学活动经验的结构化既是数学知识结构的建构过程,也是数学思维的递进发展和生长过程。在数学活动中给予学生充足的空间,让学生在与同伴的合作交流中、在做与思的密切配合中自主建构,学会整体 感悟 、主动 迁移 、主动 适应 ,多方 位、多角 度地思考问题,这样的活动经验有助于学生逐步形成结构化思维,并在今后的学习活动中不断影响学生的思维方式,促进学生各方面能力的发展。
3.从感知到内化,推动学生数学素养的提升。
数学素养是一种内涵丰富的主体结构,包含多层次的数学能力。数学活动经验结构化不仅包括学生在经历知识形成和演变的过程中获得逐步完善的认知结构,还包括获得日趋娴熟的数学技能、习得有效的问题解决方法、感受数学知识在现实生活中的广泛应用以及形成对数学学习的积极情感、态度。学生数学活动经验结构化的过程就是将感知的数学知识内化成自身能力的过程。数学活动经验结构化是提升学生数学素养的应有之义。
二、数学活动经验结构化的实施策略
(一)构建知识网络,让经验从“零散”走向“系统”
1.进行个性化教学,形成知识体系。
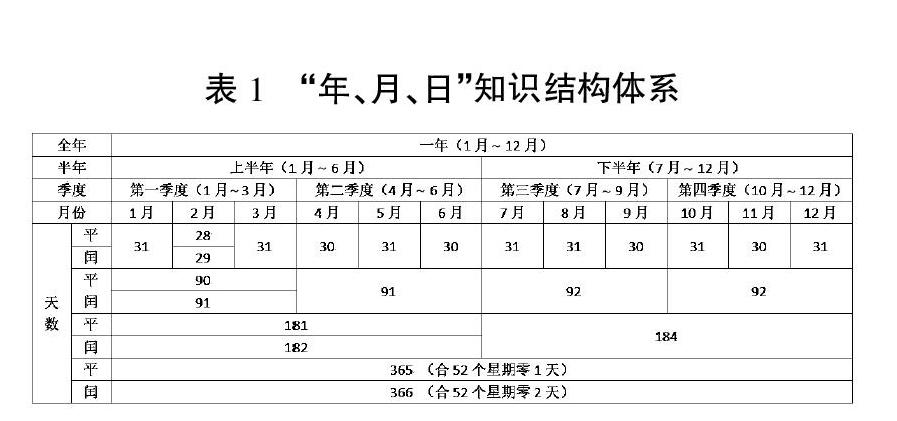
开发结构化学材,设计学生自主学习单,是知识经验系统化的有效途径,能在一定程度上满足学生个性化的学习需求。如苏教版三下“年、月、日”单元的知识点比较琐碎,涉及的概念多而杂,教师设计表1,让学生自主填写。这样做,将有助于学生对已有知识经验进行系统整理,从而主动建构起“年、月、日”单元结构化的知识体系。
2.借助思维导图,建构知识网络。
利用思维导图对所学单元或同领域的知识内容进行整理与复习,有利于学生建构知识网络,能有效地促进学生数学活动经验结构化。下图 1所示的就是三年级学生在学完“长方形和正方形的周长、面积”后自主整理形成的思维导图。周长和面积是非常重要但学生特别容易混淆的两个概念,利用思维导图进行整理,有助于学生明晰两者的本质含义,整体把握两者间的联系和区别,主动建构自己的认识结构和学习经验。
(二)挖掘内涵关联,让经验从“个体”走向“整体”
1.整体思考,深化内涵。
教师应基于学生的已有知识经验,将课时内容与单元内容、同领域内容联系起来,从而使知识的内涵不断丰富和深刻。教学苏教版三下《认识整体的几分之一》,教师以如下情境导入新课:把一个桃平均分给两只小猴,每只小猴分得这个桃的几分之几?然后开展如下教学活动。
(1)分4 个、6个、8个、12个桃提问:桃的总个数不同,每一份的个数也不同,为什么都可以用来1/2表示?
(2 )分12个桃提问:都是12个桃,为什么表示每份的分数不一样呢?
比较:今天学习的分數和以前学习的分数相比,有什么不同?又有什么相同的地方?
(3)游戏拓展:出示9 颗糖果
提问:谁能拿对这些糖的1/3,谁能拿对剩下的 糖的1/3?都是 拿1/3,为什 么一 人拿 了3 颗,一人只拿了2 颗呢?
上例中,教师先是通过两只小猴分一个桃,引导学生复习三年级上学期已经学过的一个物体的几分之一。接着,精心设计分桃活动,让学生充分体会整体的几分之一,并通过对比认识新旧知识之间的联系和区别,抽象出分数的本质:无论是一个物体还是一个整体,把它平均分成几份,每份就是它的几分之一。最后,通过游戏拓展延伸,让学生思考一个整体的几分之一是多少,为本单元下一课时做好准备;同时让学生体会整体变了,它对应的1/3的个数就变了,这里的“整体”其实是五年级要学习的单位“1”的雏形。这样的活动设计,沟通了三个阶段分数知识的内涵联系,从单一的“认识整体的几分之一”走向对分数这一知识体系的整体认知,学生的思维和能力也能得到深入的发展。
2.宏观引导,活化思维。
在教学过程中,如果教师具有大格局、大视野,将一课的教学活动置于整个学科体系和学生的能力体系中去思考,往往能抓住学生思维生长的最佳时机,让学生的思维由低阶走向高阶。如执教苏教版四下《确定位置》一课,特级教师周卫东进行了巧妙的情境创设,将课题命名为《小鸭在哪里》,首先引导学生观察思考:第一次,小鸭沿直线走,向右走了5 格,这时只有一个方向,一个距离;第二次,小鸭在一个面上走,第一列第二行,这时有几个方向、几个距离?分别是什么?整节课都围绕“小鸭在哪里”这一情境展开教学,从复习用一维的数轴来表示位置到成功引导学生感受并自己创造二维平面坐标系——用数对来表示小鸭的位置。其实,教学到这儿,本课的教学目标已然达成。但周老师并没有 就此“收 手”,而是 接着 追问 :同学 们想 想看 ,假如小鸭还想继续往水下走,小鸭又会在哪里呢?这时又需要几个方向、几个距离来表示它的位置呢?这样的设计足见教师的宏观视野,活动中 学生 的思 维由 点及 线、由线 到面 、由面 成体 ,浑然一体,学生的空间观念、想象力不断发展,数学思维在教师的引导下一次次被激活,整体的、结构化的数学活动经验不断生长。
(三)提升多元素养,让经验从“单一”走向“全面”
1.多重活动,深度建构。
让学生亲身经历知识产生和演变的生动过程,通过多重层层深入的活动感知知识的内涵,学生才能将前人智慧的结晶内化成自己的经验,从而对知识有多元化的理解。如教学苏教 版三 上《认 识周 长》一课 ,教师 设计 了如 下活 动:(1 )剪 一剪 ,体 验周 长与 边线 的关 系;(2 )描 一描 ,理 解周 长的 概念 ;(3 )指 一指 ,加 深对 周长的体验;(4)辨一辨,明晰周长的组成;(5 )量 一量 ,学 会周 长测 量方 法;(6 )练 一练 ,灵活计算图形的周长。在剪一剪、描一描、指一 指、辨一 辨、量一 量、练一 练等 多重 活动 中,学生对周长概念的理解不再是一句定义,而是全 面的 、生动 的、鲜活 的体 验和 感悟 ,对周 长概 念的建构也逐渐从浅显走向深入。这样的数学活动经验结构化的经历对学生以后学习图形的面积、立体图形的体积等都具有积极、正面的意义。
2.技术支撑,全面发展。
在教学中巧妙运用与课程内容相关的学具 、软件 、视频 等信 息技 术辅 助教 学,有助 于提 高学生运用学习工具的能力,使他们充分感受数学在生活中的广泛运用,从而能有效促进他们的全面发展。如教学苏教版四下《多边形的内角和》一课,教师组织学生开展如下活动:(1)画一画,每人利用 Numberkiz、几何画板等软 件的 多边 形功 能任 意画 一个 五边 形;(2 )算 一算,选择你喜欢的方法算出五边形的内角和,并把你的研究成果截图或拍照上传到班级百 度网 盘中 ;(3 )说 一说 ,在 小组 里说 说你 是怎样探究五边形内角和的;(4)欣赏 FAST 天眼系统视频。
上例中,教师引导学生运用 Numberkiz、几何画板等数学教学软件自带的功能量一量、拼一拼、分一分,探究多边形内角和的计算公式;让学生通过推屏展示自己的研究轨迹,并利用百度网盘分享自己的想法,学习他人的作品;通过观看视频了解多边形内角和在生活中的运用,感受科技与数学的完美融合。这样的探究活动不仅有利于培养学生的观察、推理、归纳等数学思维能力,也有助于提高学生的信息技术应用能力。这样的数学活动经验结构化的经历能使学生的素养得到全面提升,从而更好地适应未来。
3.回顾反思,学会迁移。
经常性的回顾与反思不仅有助于提高学生的归纳总结能力和数学表达能力,还有利于学生将提炼、总结出的探究活动的方法、途径等活动经验迁移到以后的学习中去。如教学苏教版五下《解决问题的策略:转化》一课,课尾,教师引导学生回顾:我们学过的哪些数学知识运用过转化策略?是把什么转化成了什么?
生1:推导平行四边形、梯形、三角形的面积计算公式,我们将它们转化成了长方形。
生2:推导圆形的面积计算公式,我们把圆形转化成了长方形。
生3:小數乘法和除法,我们将小数转化成了整数来计算。
生4:异分母分数相加减,我们是先通分,把异分母分数转化成同分母分数来相加减的。
在学完转化策略后,引导学生通过回顾以往的学习举出运用转化策略解决问题的例子,一方面能加深学生对转化策略的理解,另一方面能让学生感受到数学知识的融会贯通,能有效促进学生的数学活动经验结构化。
综上所述,要促进学生的数学活动经验结构化,不仅对学生提出了更高的要求,也对教师的专业素养提出了更大的挑战。需要教师以整体观念为抓手,以自主建构为核心,以发展思维为导向,以培养数学素养为目标追求,引导学生感受知识之间的纵向与横向联系,体验数学知识发生、发展的全过程,推动学生的数学经验走向系统化、整体化、全面化,让数学活动真正焕发持久的生命力。

