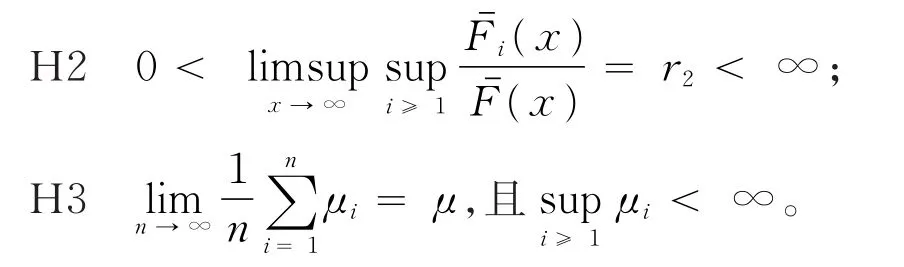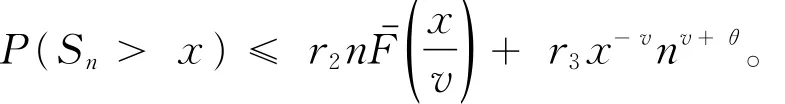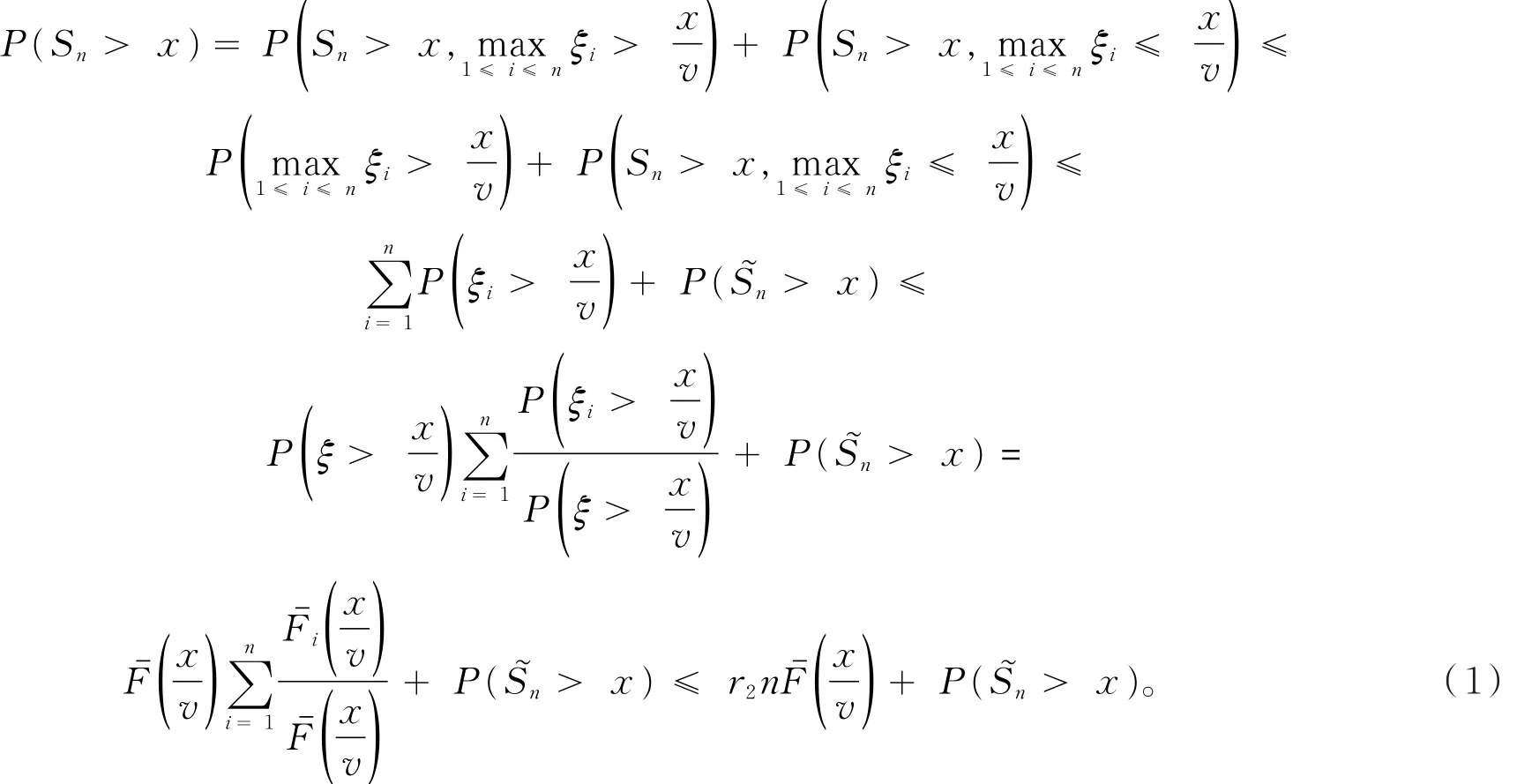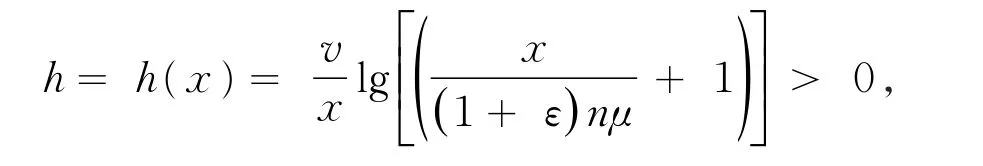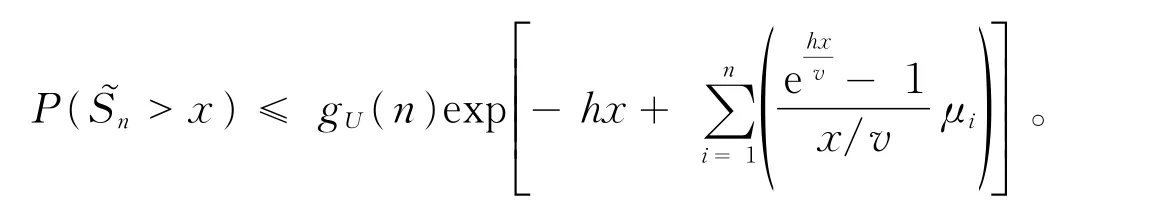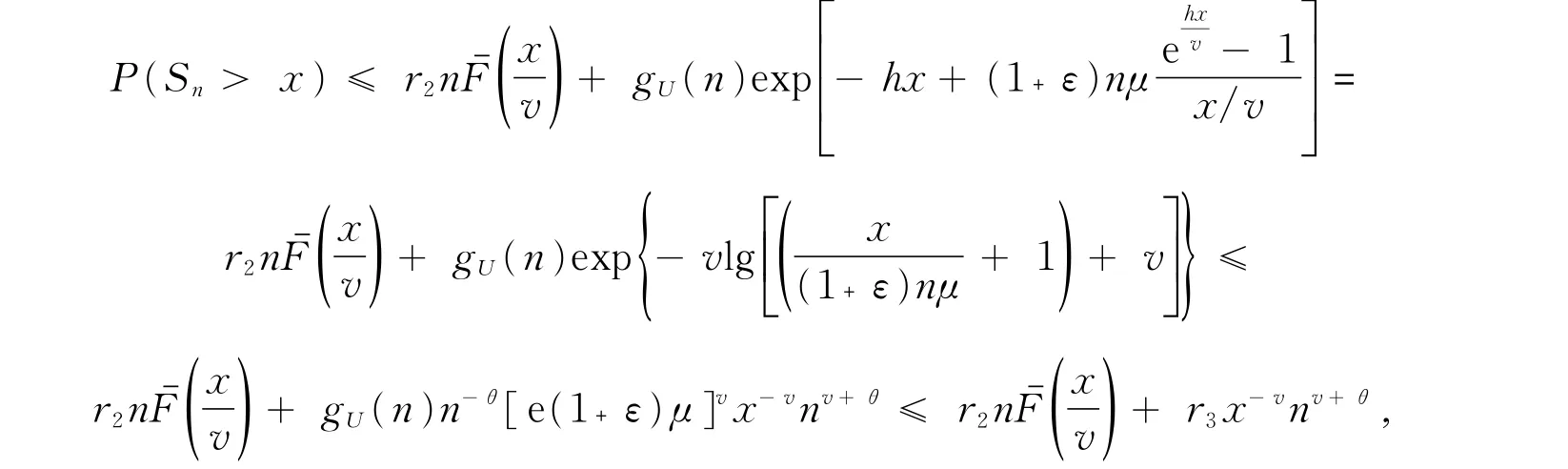一个宽上限相依随机变量的概率不等式
于海芳
(朝阳师范高等专科学校 数学计算机系,辽宁 朝阳 122000)
0 引言
随着大数据时代的到来,概率理论与数理统计理论作为大数据理论学习的基础知识显得越来越重要。概率不等式是概率理论的重要研究部分,概率不等式在证明精确大偏差、强大数定律、完备收敛等概率理论中起到重要作用。尤其是在概率理论的大偏差方向,一个好的随机变量的概率不等式对于在求解精确大偏差的上、下界中的作用更为显著。一个好的相依随机变量的概率不等式,能得到比较好的精确大偏差的上界和下界。本文设{ξi,i=1,2,…}是一个随机变量序列是 {ξ,i=1,2,… }的前n项部分和。当 {ξ,i=1,2,… }是一个随机变量ii序列,各自对应的分布为 {Fi(x),i=1,2,… }(其中Fi(x)=P(ξi≤x),x∈ R)。文献[1]提出:设{yi> 0,i= 1,2,…},y> max1≤i≤n{yi},0 证明过程详见文献[1]。在引入相应的概率不等式后,文献[2]给出了D族END随机变量的随机和的精确大偏差,文献[3]得到了索赔盈余风险模型中精确大偏差,文献[4]推广了延拓负相依风险模型中的精确大偏差,文献[5]和[6]分别给出了延拓负相依和宽相依随机变量序列条件下的精确大偏差的结论,文献[7]和[8]在带有随机利率条件和NA条件下得到了精确大偏差的渐近结论。本文主要研究了带宽上限相依的随机变量序列,得到了一个宽上限相依随机变量的概率不等式,旨在为概率论不等式理论提供一个新的有用的结论,并将在研究精确大偏差、破产概率等概率理论中起到重要作用。 设{ξi,i=1,2,…}是一个存在有限期望的、非负的、不同分布的随机变量序列,对应的分布为 {Fi(x),i=1,2,… },对应的期望为 {μi,i=1,2,… },且 {ξi,i=1,2,… }满足如下条件。 定义1[6]设{ξi,i=1,2,…}是一个随机变量序列,对于每一个有限的正整数n,存在某个有限的正数gU(n),使得对所有的xi∈ (0,∞),i=1,2,…,n,当 成立时,称{ξi,i=1,2,…}是宽上限相依的随机变量序列,称gU(n)为{ξi,i=1,2,…}控制系数。 定义2[5]设ξ是一个取值非负的随机变量,对应的分布为F(x),称 引理1[6]当{ξi,i=1,2,…}是一个非负的、宽上限相依的随机变量序列,则有: ① 如果{fi(·),i≥ 1}是非降的函数序列,则{fi(ξi),i≥ 1}也是一个宽上限相依; ②对于每一个正整数n,有 特别地,如果{ξi,i=1,2,…}是一个宽上限相依的随机变量序列,则对于每一个正整数n和任意的s> 0,有 定理1设ξ是一个取值非负的随机变量,对应的分布为F(x),存在有限的期望μ;设{ξi,i=1,2,…}是一个非负的、宽上限相依的、不同分布的随机变量序列,控制系数为gU(n),对应的分布为{Fi(x),i=1,2,…},对应的期望为{μi,i=1,2,…},满足下列假设条件: H1 存在某个正数θ∈(0,1),使得 则对于任意的v> 0,存在与x和n无关的r3=r3(v)> 0,使得对于所有的n∈Z+和充分大的x,有 证明对于任意的v> 0和任意的θ∈(0,1),n∈ Z+,记由假设条件 H2 知当x充分大时,则有 此处利用截断误差的方法来估计(1)式中P(S͂n>x)的上界。对于任意的ε∈(0,1),设 则当n→∞时有x→∞,从而有h↓ 0,h将在后面用到。由马尔科夫不等式可得 由{ξi,i=1,2,…}是一个宽上限相依的随机变量序列和引理1的①可知,{ξ͂n,n=1,2,…}仍是一个宽上限相依的随机变量序列。由引理1的②则有 对于任意的ε∈(0,1),当n充分大时,x充分大,则有 将(3)式代入(2)式,整理可得 由于不等式ln(a+x) 由假设条件H3,当n较充分大时可有 由(4)式有 将(5)式代入(1)式中,当x充分大时可得
1 预备知识

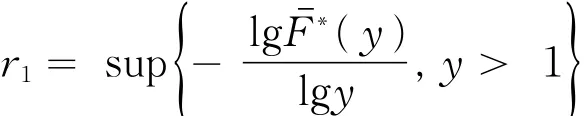
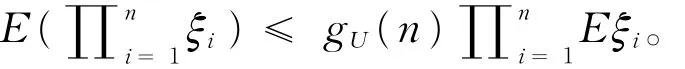
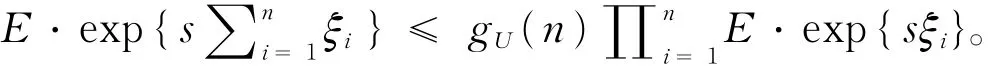
2 宽上限相依随机变量的概率不等式