LNG储罐内罐小孔泄漏工况下温度场数值模拟
张 娜 李兆慈 郭志超
中国石油大学(北京)油气管道输送安全国家工程实验室/城市油气输配技术北京市重点实验室, 北京 102200
0 前言
在LNG产业链中,储存是重要的一环。天然气低温液化后经远洋运输到达世界各地LNG接收站,接收站既是海上LNG运输的终点也是陆上天然气供应的起点[1]。储罐是接收站内最重要的储存设备,它的安全至关重要。接收站的储罐体积庞大,结构复杂,内罐工作在-162 ℃左右的低温环境,因此储罐在安全运行方面存在诸多需要注意的问题[2]。随着LNG储存设施大型化趋势和高安全性的要求,全容罐因为具有更高的安全性得到了广泛应用[3]。LNG储罐作为接收站最核心的建筑物,是重大危险源,一旦发生事故将会造成巨大损失。当储罐因为人为操作不当、设备损坏、管道破裂等问题发生LNG泄漏时,由于LNG是-162 ℃的深冷液体,泄漏出来的低温液体会对设备造成低温冲击,危害储罐结构的安全[4]。如LNG泄漏于地面时,会迅速从地面、周围环境吸收热量,蒸发为气体。LNG全容罐分内罐和外罐,在设计和建造上能容纳所储存的低温液体以及液体蒸发后产生的低温气体。由于LNG接收站一般位于沿海地带,可能发生地震等自然灾害,增加了LNG储罐内罐泄漏的风险。所以采用合理的方法对LNG储罐内罐泄漏进行模拟研究,对于外罐壁厚的设置、制定发生泄漏时采取的应急措施都具有重要意义。
1 LNG储罐泄漏研究方法
因低温导致设备材料断裂,从而引起的储罐泄漏,一般可根据泄漏口面积大小和泄漏处高度等因素分成两类[5]:一类是大面积泄漏,在较短时间内储液大量漏出,瞬间产生大量BOG气体,可能在储罐内形成瞬间高压发生爆炸[6];另一类是有限孔泄漏,储存的液体沿小泄漏口缓慢流入绝热层,破坏绝热层结构,对储罐的正常运行造成影响。内罐小孔泄漏是目前最易发生的泄漏工况,本文主要针对LNG内罐小孔泄漏工况进行计算模拟。
对于LNG储罐泄漏问题,早期通过现场模拟实验,在野外搭建与真实事故完全一致的场景,重现当时的后果影响,得到最真实的数据资料。但这种现场试验随机性很大,且需花费大量人力物力,得到的结果仅对某一特定的事故有帮助,但对类似事故参考意义不大,因此需要更简单的具有普适性的方法[7]。通过物理模型构建类似实际情况,可在实验室完成的小型泄漏模拟实验来研究实际LNG泄漏扩散规律。研究LNG泄漏扩散过程的物理模拟一般采用风洞试验[8]。20世纪70、80年代,MeroneyR N[9]已经模拟出LNG高空和地面释放情况下的LNG扩散。
数值模拟是应用比较普遍的一种借助计算机完成的LNG储罐泄漏扩散模拟方法。这种方法无需设置实验,可借助不同的数学模型完成,经济省时,可以得到详尽的结果。随着计算机计算能力的不断提高,加上有限容积法、有限元分析法等数值计算方法的发展,基于数值计算的计算流体力学(CFD)方法得到了蓬勃发展[10]。
LNG泄漏后的扩散过程可通过速度、浓度和温度进行描述,其控制方程包括连续性方程、动量方程、能量方程、扩散方程、湍流动能方程、湍流动能耗散方程[11]等。
现场实验会耗费较大的人力、物力和财力,同时外界的环境变化复杂,在某些情况下难以获取理想的数据。风洞实验在低风速和低雷诺数条件下进行比较困难[11]。几种方法互有长短,实际研究中可综合运用,但鉴于数值模拟的耗时短、成本低以及高度可重复性,近几年成为此类研究中最广泛使用的方法[12]。
对比LNG泄漏扩散的各种研究方法可知,CFD模拟具有较好的适用性,但要准确模拟LNG泄漏扩散过程,对初始条件、边界条件设置要求较高[13]。同时CFD模拟还存在一些问题需要解决,如过分简化处理源项和地面传热方式,对于关键影响因素的敏感性分析不足等。
2 内罐泄漏温度场计算模拟
随着内罐小孔泄漏的持续,内罐受影响区域逐渐向保温层外侧和底部发展,危及LNG外罐的安全。
在LNG储罐内罐发生泄漏时,LNG会沿有限孔缓慢流出,再沿着储罐内壁外的弹性玻璃纤维毡流入环形空间的绝热层中。绝热层由弹性毡、膨胀珍珠岩和泡沫玻璃砖组合而成[14]。以 20 000 m3双金属全容式LNG储罐为例,内罐高度30 m,内罐罐径(直径)30 m,外罐罐壁高度31 m,外罐罐径(直径)32.378 m,外罐拱顶高度4.66 m。内罐由底板、顶板及10层壁板组成,外罐由底板、顶板、10层壁板及梯子栏杆组成。
由于内罐整体高度为30 m,所以每层壁板高度为3 m。内、外罐壁每层壁板厚度见表1。
表1 内、外罐各层壁板厚度表
Tab.1 Thickness of each layer of the tank innerwall and outerwall

罐壁板层内罐壁板厚度/mm外罐壁板厚度/mm第1层1612第2层1212第3层810第4层810第5层68第6层68第7层68第8层68第9层68第10层68
储罐绝热层结构见图1,内壁绝热材料的厚度及导热系数等参数见表2。
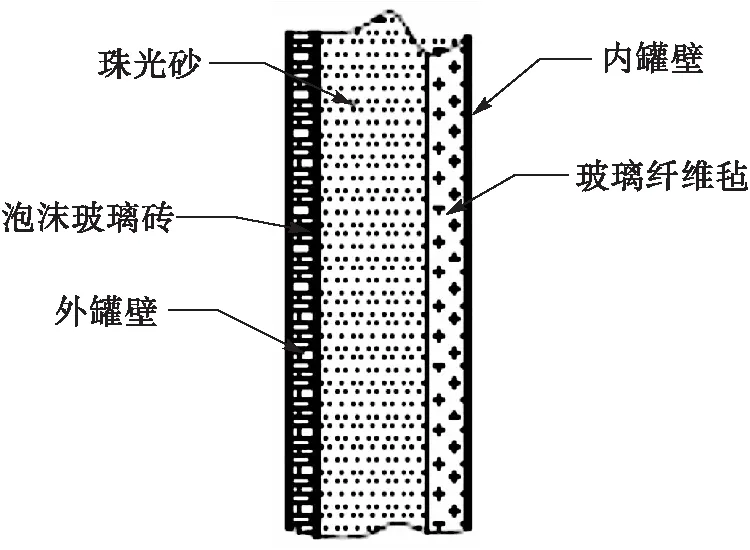
图1 罐壁绝热层结构示意图Fig.1 The wall insulation of the tank
表2 储罐罐壁绝热层数据表
Tab.2 Wall insulation of the tank
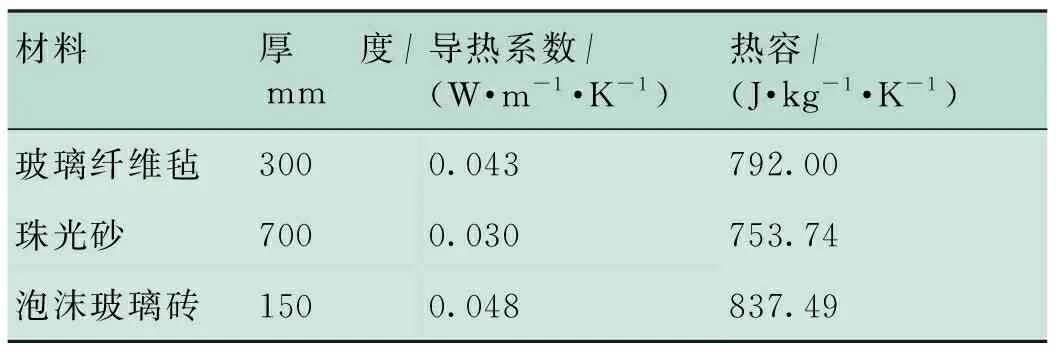
材料厚度/mm导热系数/(W·m-1 ·K-1)热容/(J·kg-1 ·K-1)玻璃纤维毡3000.043792.00珠光砂7000.030753.74泡沫玻璃砖1500.048837.49
绝热材料是由气相与固相构成的多孔性组织,固体材料内部存在互相连通的气相空间,这给LNG泄漏提供了一条渗流通道,因此LNG储罐内罐泄漏模拟可采用多孔介质模型[15]。
在内罐泄漏条件下,对储罐的温度边界条件作以下假设:外罐壁初始温度取正常操作条件下的环境温度20°C,外罐壁与空气的对流换热系数取25 W/(m2·K);储罐内LNG温度为-162°C,内罐温度与储液温度相同。不考虑LNG泄漏时的相变,外罐壁和罐底部绝热层的下部均为绝热壁面,外罐壁顶部也设为绝热壁面。由此得到稳态时罐壁绝热层的温度分布,见图2。

图2 稳态温度分布图Fig.2 Temperature distribution in steady state
储罐壁高30 m,故i的取值范围在0~3 000,在距离罐底10 m(i=1 000)处设置泄漏工况,泄漏孔径为10 mm,泄漏点流速为0.02 m/s。
考虑泄漏点处对流换热,设置泄漏点(i=1 000)处温度为LNG的温度,与上下边界进行对流换热,由傅立叶定律和牛顿冷却公式可知其热流量相等,即:
(1)
式中:h为对流换热系数,W/(m2·K);Tw为壁面温度,℃;Tf为流体温度,℃;T为绝热层温度,℃;λ为介质导热系数,W/(m·K);Y为内壁高度方向。
其中,对流换热系数h是一个与流体密度、比热容、流速、黏度、导热系数有关的复杂函数,h=f(ρ,cp,λ,u,l,μ),可通过计算雷诺数Ref、努赛尔数Nuf和普朗特数Prf得到[16],具体计算按式(2)。
(2)
式中:u为流体流速,m/s;l为当量长度,m;μ为流体黏度,m2/s。对于非圆形截面的槽道,l取当量直径作为特征长度de。
(3)
式中:Ac为槽道的流动截面积,m2;P为润湿周长,即槽道壁与流体接触面的长度,m。
再计算普朗特数:
(4)
式中:Cp为流体比热容,J/(kg·K);a为流体导热系数,W/(m·K)。
最后再由努赛尔数求得流体的对流换热系数h:
(5)
将内罐泄漏后的罐壁传热简化成二维非稳态对流换热问题,先求得泄漏流体在罐壁内的流场分布。对弹性多孔介质单相不可压缩流体不稳定渗流问题,其运动方程为:
(6)
式中:ν为流体泄漏速度,m/s;K为介质渗透率,μm2。
对于二维平面:
(7)
对于弹性孔隙介质,其状态方程(多孔介质和液体都是可压缩的):
φ=φa+Cf(p-pa)
(8)
式中:φ为孔隙介质度;Cf为流体的压缩系数;φa为标准大气压下孔隙介质度;pa为标准大气压,Pa;p为流体压力,Pa。
对于弹性液体:
ρ=ρaeCL(p-pa)=ρa[1+CL(p-pa)]
(9)
式中:ρ为液体密度,kg/m3;ρa为标准大气压下液体密度,kg/m3;CL为液体弹性压缩系数。
单相流体的连续性方程为:
(10)
将运动方程和状态方程代入连续性方程可得:
(11)
通过对设置的储罐内壁绝热层进行网格划分,确定出边界点、角点和内点,再对二维非稳态渗流压力方程进行离散,最后采用TDMA算法加快迭代计算速度,由此计算模拟可得到LNG泄漏至内罐壁的流场分布,其横坐标为内壁厚度,纵坐标为内壁高度,罐底至泄漏点即i=1 000下方的压力分布见图3。
由图3可知,在计算步长内,其压力在泄漏点处最大,逐渐向下削弱。通过对x和y方向上的压力求偏导,可计算得到二维速度场的分布,图4为罐壁泄漏点(i=1 000)下方二维速度分布矢量图。
由模拟结果可以看出,由于罐壁绝热层材料物理特性不同,其渗透扩散速率也不同。将模拟计算得到的流场分布与温度结合,将模拟计算得到的速度分布作为对流扩散项添加到二维非稳态对流换热方程中,即完成流场温度场的耦合。
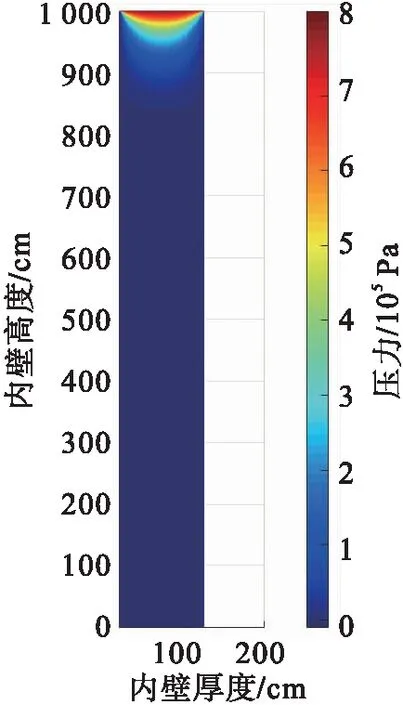
图3 泄漏点下方压力分布图Fig.3 Pressure distribution below the leak point
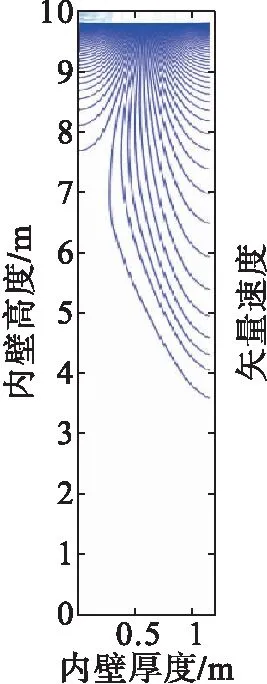
图4 速度分布矢量图Fig.4 Speed distribution vetor
(12)
对式(12)进行离散,采用中心差分形式,对角点、边界点和内点分开离散,再用Gauss-Seidel迭代法计算内壁绝热层区域内的内点,得到LNG液体泄漏后在罐壁内的温度分布(泄漏点i=1 000)。
由图5的温度分布云图可知,随着计算时间的推进,泄漏液体向下扩散程度大,且越靠近泄漏点处泄漏速度越大,温度变化梯度也随之增大。
3 Fluent软件模拟验证
Fluent软件是采用有限容积法对控制方程进行离散并求解的,离散方程有清晰的物理解释,其内置各类模型及方法可用于求解不同流体力学问题,针对渗流问题,亦采用多孔介质模型进行模拟。
Fluent软件中涉及到传热问题时,其基本守恒方程为质量守恒、动量守恒以及能量守恒方程[17]。多孔介质模型本质上其实仅在动量方程上附加源项;若涉及传热问题,可以只修改能量方程的传导通量及瞬态项[17]。实际上,Fluent软件并不存在独立的多孔介质区域,模型假设多孔介质固体区域为流体区域,对流入其中的流体设置阻力系数以达到渗流效果[18];如涉及热传导,设置多孔区域孔隙率,通过孔隙率换算出有效热导率,将其添加于能量方程中以达到热量传递效果[19]。计算得出绝热材料的阻力系数见表3。
使用ANSYS workbench工作平台建立二维模型,合理划分网格后,将参数条件导入Fluent软件中进行模拟,在上述相同的温度边界条件下,通过稳态求解的方法得到罐壁的温度场分布,见图6。
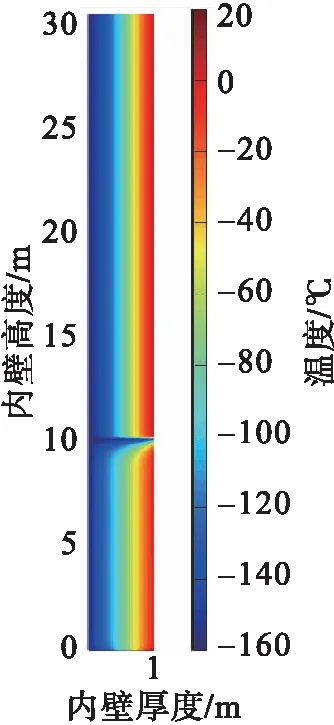
a)100时步a)100 time steps
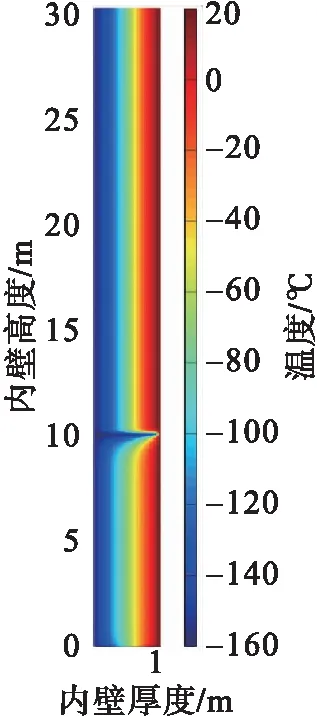
b)500时步b)500 time steps
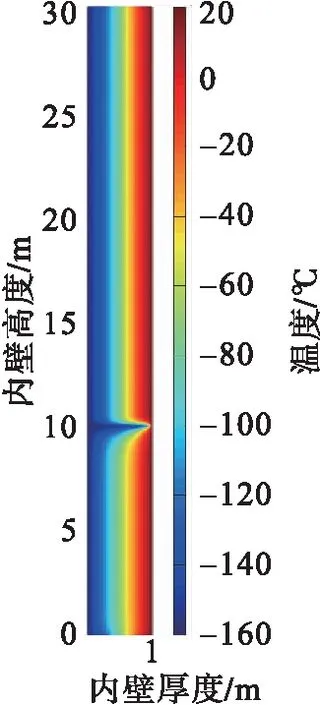
c) 1 000 时步c)1 000 time steps

d) 1 000 时步放大d)1 000 time steps amplification
表3 多孔介质模型各绝热材料参数表
Tab.3 Insulation materials parameters in porous model
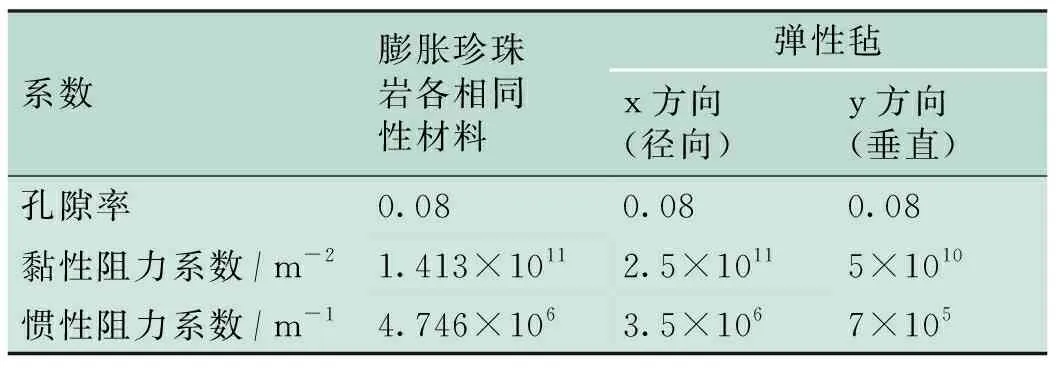
系数膨胀珍珠岩各相同性材料弹性毡x方向(径向)y方向(垂直)孔隙率0.080.080.08黏性阻力系数/m-21.413×10112.5×10115×1010惯性阻力系数/m-14.746×1063.5×1067×105

图6 罐体稳态温度分布图Fig.6 Temperature distribution of the tank in steady state
再模拟泄漏工况,泄漏点为距储罐底部10 m处,泄漏孔直径10 mm,泄漏热温度条件与上述一致。LNG从泄漏口流出,采用多孔介质模型,按表3设置模拟参数,获得不同时刻罐体温度分布,结果见图7。

图7 LNG储罐泄漏工况下温度分布图Fig.7 Temperature distribution diagram of LNG tank under leakage conditions
由图7可以看出,内罐泄漏时,漏液先向下聚集,靠近内罐壁的弹性毡快速降温至LNG温度,当低温液体到达罐底时,低温LNG液体富集底部,而后沿罐底逐渐渗透到膨胀珍珠岩中,最后扩散到整个绝热层。经计算,泄漏后约26 h低温液体渗透至全部绝热层中。
4 结论
通过Fluent软件模型和CFD计算得到了相似的结果,在计算时长和边界条件的设置难度上,Fluent模型要优于CFD直接计算,所以如果有模型符合应用场景时,可以选取模型进行计算。
LNG内罐发生泄漏时,漏液先向下聚集,呈不对称分布,温度分布表现为靠近泄漏源处的弹性毡首先降温到LNG温度,且此处的温度梯度较大;而后沿罐底逐渐渗透到膨胀珍珠岩中,随着泄漏时间的不断推进,漏液最后扩散至整个内壁绝热层。但由于次容器与泡沫玻璃砖的存在,外罐壁的温度与外界温度相差不到1 ℃,起到了良好的绝热保冷效果。

