基于改进的SWAT 模型的山地流域吸附态总磷负荷模拟
龙天渝,钟少荣,李业盛,郑岐全,刘 敏
(重庆大学 三峡库区生态环境教育部重点实验室,重庆 400045)
随着点源污染管控力度的加大,非点源污染已成为水体污染的主要原因[1]。2015年,国家正式发布《水污染防治行动计划》,提出要全面控制工业、农业和城镇污染物排放,深化污染物总量控制。明确非点源污染的时空效应,研究非点源污染的产生和运移机制,识别关键污染源区是开展非点源污染治理的关键。非点源污染从形式上可划分为吸附态和溶解态两种类型。吸附态非点源污染是指污染物以陆面上被侵蚀泥沙为载体,在径流的作用下迁移进入水体所形成的污染。磷主要以吸附态的形式进入水体,在三峡水库,80%以上的磷是以吸附态形式存在[2]。
非点源污染具有起源分散、随机性强、污染范围广等特点,因此,监测识别非常困难,特别是大型流域或区域。应用数学模型进行模拟和分析是研究非点源污染最有效、最直接的方法。通过构建数学模型,从景观生态学和系统动力学角度出发,研究自然特性和人类活动对水环境的影响已成为当前非点源污染研究的热点之一。在流域尺度的非点源污染模型中,SWAT模型被广泛采用[3-7]。吸附态污染是陆面上被侵蚀土壤在降雨形成的地表径流的迁移作用下伴随着入河泥沙所形成的污染,因此,产沙量的模拟是吸附态污染负荷模拟的基础。由于被侵蚀的土壤在迁移过程中会产生部分沉积,因此最终进入水体的泥沙量总是小于被侵蚀的土壤量。在SWAT模型中,产沙量的模拟采用的是修正的土壤流失方程(MUSLE)。在该方程中,涉及到陆面泥沙输移比(陆面上被侵蚀的土壤进入水体的比例)的因子“峰值流量”和“地表径流量”,其通常采用小流域出口值,出口值不能反映泥沙输移比的空间异质性或空间分布,仅能反映整个流域形成的地表径流随时间变化所引起的泥沙输移比的变化,因此模拟结果无法确定陆面上产生泥沙以及吸附态非点源污染的关键区域,这显然不利于从源头控制和有效治理产沙和吸附态非点源污染。
为此,本文针对山地流域,提出坡面(山地流域的陆面)泥沙输移比的时空分布式,对SWAT模型中的泥沙模型进行改进,并在此基础上,构建吸附态总磷负荷模型,以山地流域,即三峡库区包含的御临河流域、小江流域、大宁河流域和香溪河流域为例,对它们的吸附态总磷负荷进行模拟。由于三峡库区为行政区域,而不是完整的流域,因此为模拟三峡库区产生的吸附态总磷负荷,采用了小流域扩大法,将库区分为御临区、小江区、大宁区和香溪区4个小区,将其中包含的流域负荷模型及其模型参数扩大到整个小区进行模拟。
1 研究区域与方法
1.1 研究区域及数据来源
三峡库区(105°44′~110°39′E,28°32′~31°44′N)处于长江上游向中游过渡的平原和四川盆地的结合地区,面积广阔,总面积约为5.8万km2。库区包括御临河流域、小江流域、大宁河流域和香溪河流域。库区内地形以丘陵、山地为主,丘陵约占总面积的21.7%,山地约占74.0%[8]。该区域属于亚热带季风性湿润气候,多年平均气温17~19℃。降水丰富,年平均降雨量为1 150.26 mm,但其空间分布不均,不同年份相差颇大,降雨主要集中在夏季,多为暴雨或大暴雨,导致库区水土流失严重。
模拟所需资料包括空间数据和属性数据等,具体来源见表1。数字高程图(DEM)和重分类的土地利用类型图见图1和图2。
1.2 坡面输沙模型
1.2.1 坡面产沙模型构建

图1 三峡库区数字高程图Figure 1 DEM diagram of the Three Gorges Reservoir area

表1 数据及来源Table 1 Data and sources

图2 三峡库区土地利用图Figure 2 Land use map of the Three Gorges Reservoir area
在陆面上被侵蚀的土壤在降雨径流的作用下迁移进入水体,形成入河泥沙。由于被侵蚀的土壤在迁移过程中将产生部分沉积,因此最终进入水体的泥沙量小于被侵蚀量。对于山地流域,坡面被侵蚀的土壤进入水体的比例通常称为坡面泥沙输移比HSDR(The hillslope sediment delivery ratio),即

式中:HSDR为坡面某单元泥沙输移比,无量纲;Y为产沙量,t;E为坡面某单元的土壤侵蚀量,t。显然,不同时刻、不同空间位置的HSDR不同,其随时空的变化而变化。对于陆面上某空间单元的土壤侵蚀量E,通常采用修正的通用土壤流失方程(RUSLE)进行计算:

式中:R为降雨侵蚀力因子,MJ·mm·hm-2·h-1;K为土壤可蚀性因子,t·h·MJ-1·mm-1;LS为坡长坡度因子,无量纲;C为植被覆盖度因子,无量纲;P为水土保持措施因子,无量纲。由式(2)和式(3)可得:

在SWAT模型中,采用改进的通用土壤流失方程(MUSLE)计算产沙量。

式中:Q为地表径流量,m3;qp为峰值流量,m3·s-1。在现有文献中,qp和Q基本上采用流域出口的实测值。
对比式(4)与式(5)可知,在MUSLE中与泥沙输移比HSDR以及降雨侵蚀力因子R有关的因子为地表径流量Q和峰值流量qp,因常采用出口值计算,因此代表的是流域空间上的平均值,不能反映产沙量的空间变异性或空间分布,以及对应的吸附态非点源污染负荷的空间分布。为此,本文针对山地流域,构建具有时空分布特性的坡面泥沙输移比HSDR,并在此基础上形成时空分布的产沙模型以及吸附态总磷负荷模型,模拟产沙量和吸附态磷负荷的时空分布,识别产沙和形成污染负荷的“关键源区”。
1.2.2 泥沙输移比的时空分布式
针对山地流域,在分析和研究了现有有关坡面泥沙输移比计算式的基础上,Broselli等[9]提出了“流动连通性”因子IC(Flux connectivity),并由其形成了HSDR的计算式。Broselli等认为,坡面某空间单元上被侵蚀土壤进入水体的比例取决于该单元与坡上单元和坡下单元的水力连通状况。坡上单元指汇流于该单元的所有单元,而坡下单元指从该单元进入到水体所经过的所有单元。假定坡上单元水力连通的程度与坡上各单元的植被覆盖率、坡度和总汇流面积成正比,而坡下单元水力连通的程度与坡长成正比、与坡下各单元的植被覆盖率和坡度成反比,得到:

式中:Dup为坡上单元水力连通分量;Ddn为坡下单元水力连通分量;----Cup为坡上各单元平均植被覆盖率,无量纲;Sup为坡上各单元平均坡度,无量纲;Aup为坡上单元的总汇流面积,m2;lw为坡下单元w的长度,m;Cw为坡下单元w的植被覆盖率,无量纲;Sw为坡下单元w的坡度,无量纲。由于0≤HSDR≤1,且HSDR应随IC非线性地单调增加,因此可近似假定HSDR与IC之间满足玻尔兹曼S形关系,即
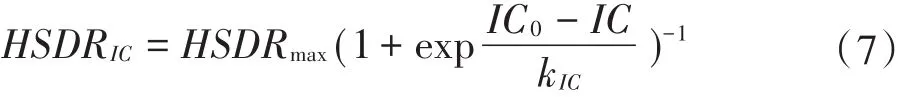
式中:IC0和k IC为参数,由实测数据率定;HSDRmax为HSDR最大值,取决于表层土壤的类型,其数值范围为0.7~0.9[10]。研究表明,采用式(7)的坡面泥沙输移比与式(3)的RUSLE结合模拟的产沙量精度明显提高[10]。
分析式(6)和式(7)可以发现,HSDRIC表征了坡面泥沙输移比的空间变化,即在坡面不同位置被侵蚀的土壤进入水体的比例不同,但无法表征降雨产生的径流等随时间变化而导致的变化。鉴于径流是迁移被侵蚀土壤的动力,且径流随时间的变化是引起坡面泥沙输移比随时间变化的最重要因素,定量表示径流强度和径流随时间变化的单元累积地表降雨径流深能综合反映坡上各单元的植被覆盖率、坡度和总汇流面积对“流动连通性”的作用,因此,采用径流深来表征与坡上各单元的水力连通程度应比式(6)更精确,这也解决了“HSDRIC无法表征降雨产生的径流随时间变化引起的坡面泥沙输移比变化”的问题。为此,假定坡上单元水力连通程度与该单元的累积地表降雨径流深成正比,而坡下单元水力连通程度与式(6)相同,重新定义“流动连通性”因子。新定义的“流动连通性”因子称为“径流连通性”RC(Runoff connectivi⁃ty),RC以及相应的HSDRRC的计算式为:

式中:H为某单元的累积地表降雨径流深,m;RC0和kRC为参数,由实测数据率定。式(9)为具有时空分布特性的HSDRRC计算式。
1.2.3 模型的验证
为对比HSDRRC与HSDRIC的模拟效果,应用式(4)和式(9)或式(7)分别对三峡库区中的山地流域——大宁河流域和小江流域的产沙量进行模拟,并将模拟结果与实测值进行对比。对于大宁河流域,根据巫溪站2006—2009年各年中4—10月泥沙观测值(1—3月为枯水期,产沙量近似为0)对模型参数进行率定,采用巫溪站2010—2013年各年中4—10月的泥沙观测值来检验HSDR的合理性和精确性。对于小江流域,选用宝塔窝站2002—2003年各年3—10月的泥沙观测值对模型参数进行率定,采用2004年3—10月的泥沙观测值进行检验。使用纳什系数(Nash-Sutcliffe effi⁃ciency,NS)和决定系数R2评价模型的合理性和精度。
本文式(3)中各因子的计算方法与现有研究成果[11-12]相同,式(8)中累积地表降雨径流深H的计算采用分布式径流曲线(SCS-CN)的方法[11],并借助ArcGIS中加权累积流函数得出其值,HSDRmax依据土壤数据分别赋值。由于三峡水库蓄水后支流的流速不大,因此不计河道内河床侵蚀产生的泥沙,坡面入河泥沙在河道内的沉积采用改进的Bagnold泥沙输移方程进行计算[13]。
表2为HSDRRC和HSDRIC的模拟精度对比。由表2可知,基于HSDRRC的产沙量模拟效果比基于HS⁃DRIC的模拟效果更佳。对于大宁河流域,在模型检验期应用HSDRRC模拟产沙量的NS值和R2值相比HSDRIC提高了14.1%和7.8%。各流域HSDRRC中参数率定结果见表3。
1.3 吸附态总磷负荷的时空分布模型
在改进了SWAT模型的产沙量计算方法后,采用SWAT模型中由产沙量计算吸附态总磷负荷的方法,用式(10)和式(11)计算该单元产生的吸附态总磷负荷[14]。

式中:LP为吸附态总磷负荷,t;A为单元面积,hm2;Cs为土壤中磷背景含量,g·kg-1;η为富集比,无量纲。由于改进的产沙模型为时空分布模型,由此形成的吸附态总磷负荷模型也变为时空分布模型。
1.4 小流域分区推广法
三峡库区为行政区域,而非完整的流域,为模拟三峡库区的产沙量以及吸附态总磷负荷的时空分布,参考有关文献[15-16],选用小流域分区推广法对三峡库区进行模拟。首先,对库区所包含的4个小流域,即御临河流域、小江流域、大宁河流域和香溪河流域,分别根据各自流域出口实测的泥沙数据率定其模型参数(HSDRRC中的RC0和kRC),并对其模拟效果进行验证(表3),然后将4个小流域模型模拟的区域分别推广到相应的御临区(YL)、小江区(XJ)、大宁区(DN)和香溪区(XX)4个区域(图3),4个区域覆盖了整个三峡库区。

表2 模拟精度对比Table 2 Comparison of simulating precision

表3 各小流域产沙模型参数的率定值及模拟效果Table 3 HSDR parameter rate setting and accuracy of each zone
2 结果与分析
2.1 三峡库区输沙量模拟
以2016年为例,4个区域的产沙量如图4所示。4个区域产沙量的空间差异明显,产沙最多的区域为大宁区,其东北部为产沙的关键源区,该区域单位面积产沙量峰值为2 154.26 t·hm-2,平均值为18.03 t·hm-2;产沙最少的区域为香溪区,其峰值为1 245.27 t·hm-2,平均值为5.98 t·hm-2。
2.2 三峡库区吸附态总磷负荷模拟
2.2.1 负荷的空间分布
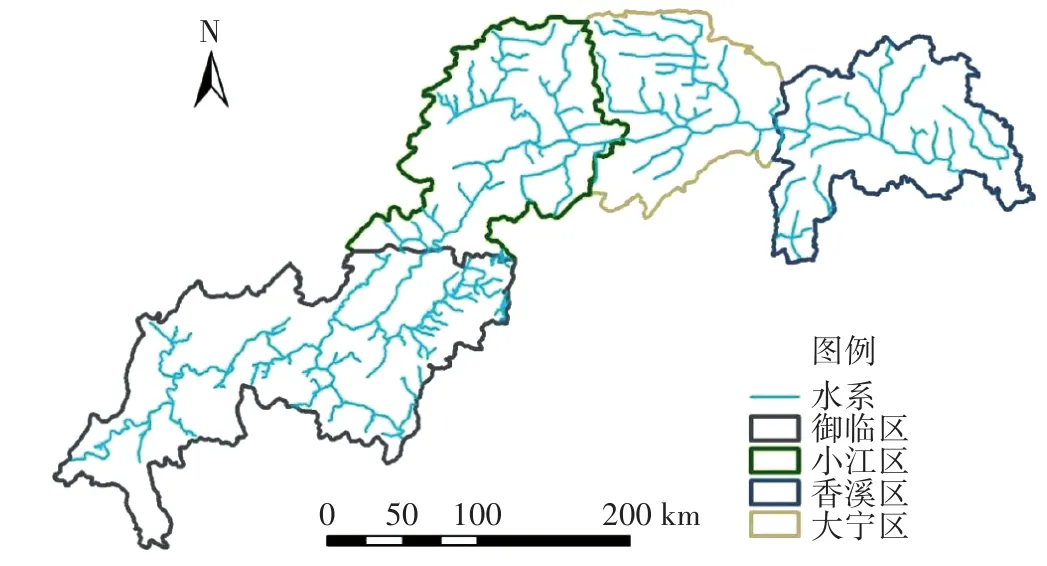
图3 三峡库区模拟分区Figure 3 The Three Gorges Reservoir area division
依据小流域扩大法汇总获得的三峡库区产沙量分布,由式(10)可以模拟出三峡库区吸附态总磷负荷,2016年的模拟结果如图5所示。从图5中可以看到,总体上负荷的空间变化较大,小江区北部负荷最高,最高达到144.6 kg·hm-2,此外,大宁区部分地域和御临区东部的负荷也较高,这些地区是负荷形成的关键源区。表4为各分区总磷负荷量和平均负荷强度(单位面积上的负荷量)。总体来说,大宁区产生的污染负荷最多,其次为小江区。整个库区平均吸附态总磷负荷强度为0.49 kg·hm-2。
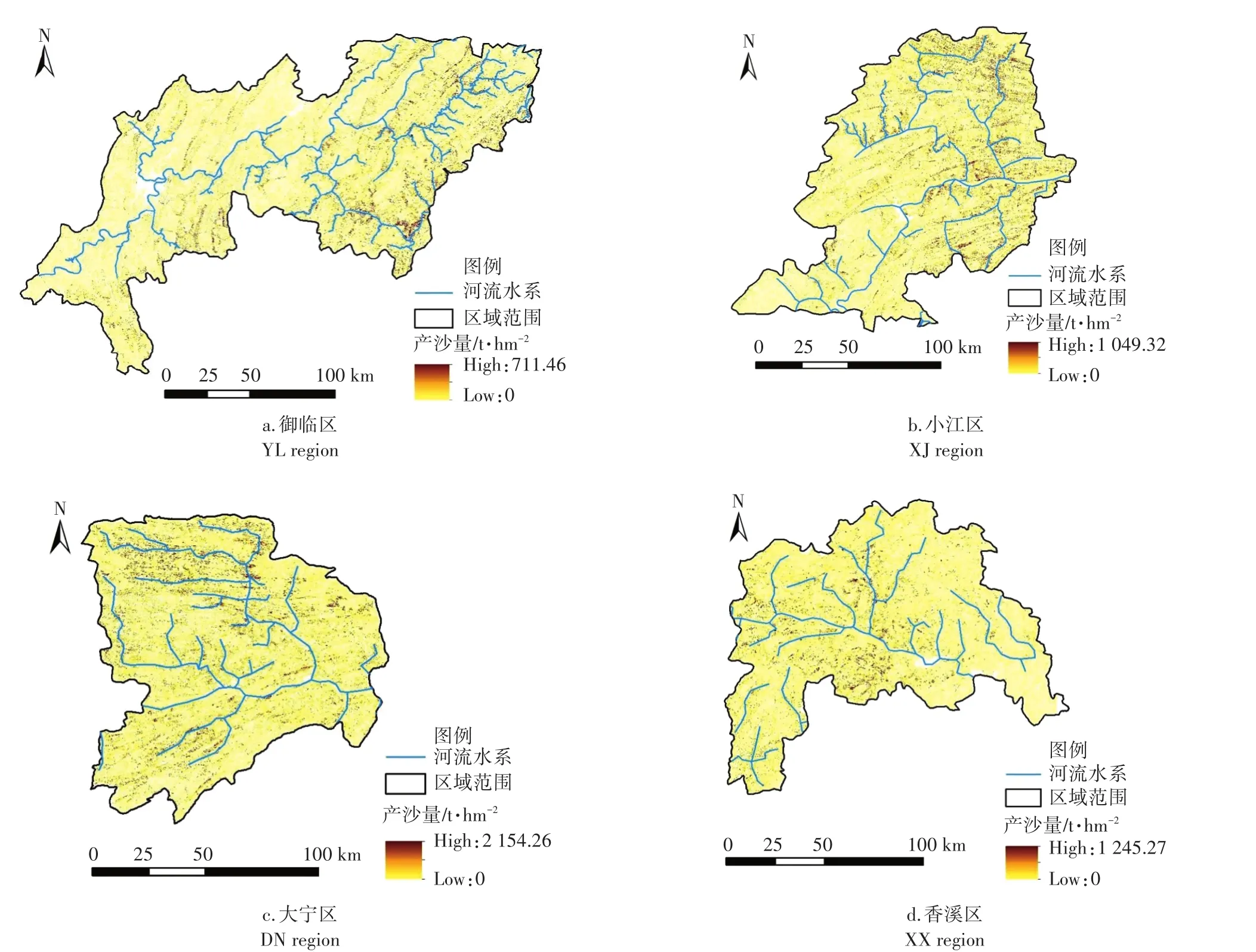
图4 4个区域的产沙量分布Figure 4 Distribution of slope sediment transport capacity in four regions
2.2.2 负荷随时间的变化
由于库区各年以及同一年中各月的降雨量不同,导致产沙量和吸附态总磷负荷随时间发生变化。图6为2007—2016年库区产沙量和总磷负荷的年际变化,图7为2007年4月—2017年6月库区总磷各月间的变化。从图6中可以看到,产沙量和吸附态总磷年际差异显著,产沙量峰值出现在2016年,约6 020万t,最小的年份为2012年,约3 610万t;吸附态总磷负荷峰值出现在2014年,约2 890 t,最小为2012年,约1 750 t。吸附态总磷负荷不仅年际差异大,由于同一年内各月降雨量不同,各月的差异也十分明显。由于每年1—3月及11—12月降雨少、雨量低,基本不产生地表径流,产沙量和总磷负荷可认为是0。从图7中可以看到,全年的污染负荷主要来源于夏季。
3 结论
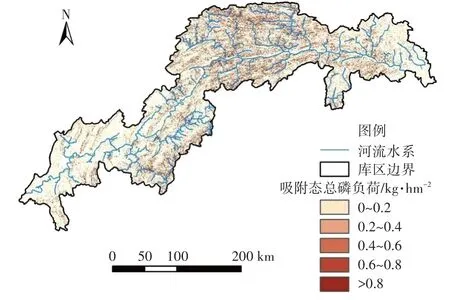
图5 三峡库区2016年吸附态总磷负荷分布Figure 5 Distribution of adsorbed phosphorus loads in the Three Gorges Reservoir area in 2016

表4 各分区吸附态总磷负荷量及负荷强度Table 4 Adsorbed phosphorus load and load intensity of each region

图6 三峡库区产沙量和吸附态总磷年际变化Figure 6 Interannual variation of slope sediment transport capacity,adsorbed phosphorus
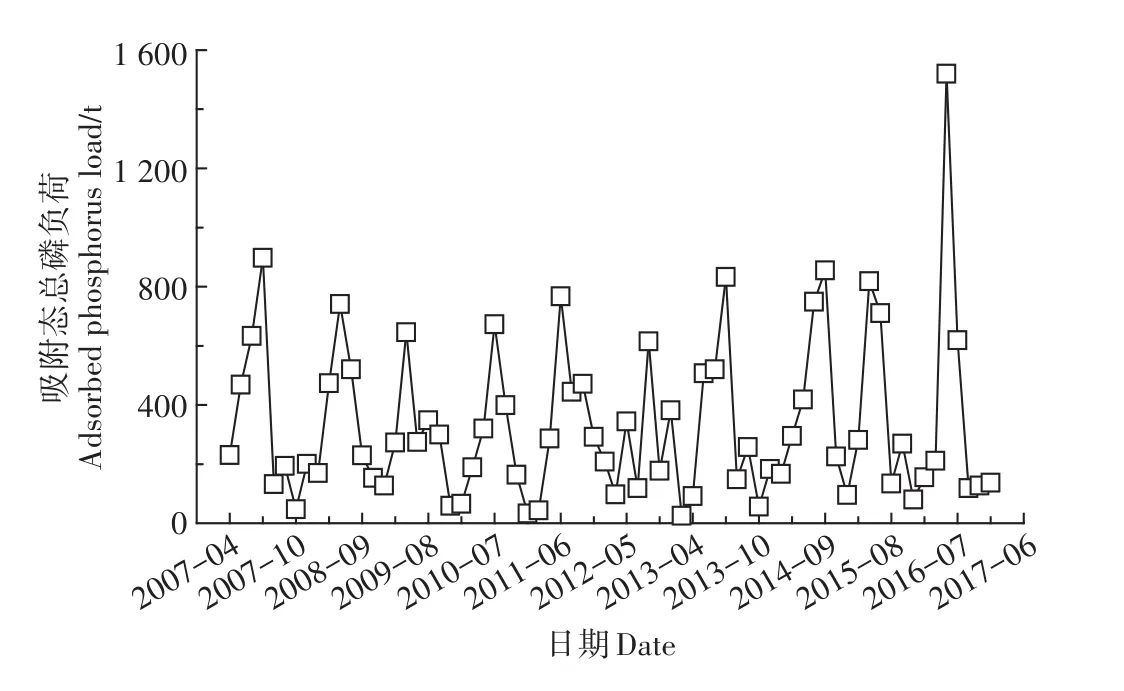
图7 三峡库区各月吸附态总磷的变化Figure 7 Monthly variation of adsorbed phosphorus in the Three Gorges Reservoir area
(1)针对山地流域,提出“径流连通性”因子,基于“径流连通性”因子形成坡面泥沙输移比的时空分布式,对SWAT模型中产沙量的计算方法进行了改进,构建了时空分布的山地流域坡面产沙模型以及吸附态总磷负荷模型。产沙量的模拟结果表明,改进后的模型不仅能模拟产沙量的时空分布,而且模拟精度高。
(2)应用所构建的吸附态总磷负荷模型,采用小流域推广法,对三峡库区进行分区模拟,实现了对吸附态总磷负荷的模拟。模拟结果显示三峡库区的吸附态总磷负荷的时空差异性大,在空间上,负荷强度从0到144.6 kg·hm-2,在大宁区和小江区,平均负荷强度较大,分别为 0.81 kg·hm-2和 0.69 kg·hm-2;同一年内各月的吸附态总磷负荷差异明显,全年的污染负荷主要来源于夏季。
(3)本文基于“径流连通性”因子所形成山地流域产沙量和吸附态负荷时空分布的计算方法可用于其他山地流域,通过模拟,获得产沙和产生吸附态负荷的关键区域,有利于吸附态负荷的有效治理。

