瘫船稳性横摇周期计算方法讨论分析

马坤，梅树猛，于津钊

大连理工大学船舶工程学院，辽宁大连116024

0 引 言

目前，第2 代完整稳性衡准的制定工作仍在进行当中，薄弱性评估方法已基本确定［1-2］。在瘫船稳性第1 层薄弱性衡准中，是通过简单的计算公式来确定固有横摇周期，但该方法没有考虑复原力臂曲线的非线性等因素的影响［3-4］。波兰在SDC 5/6/8 标准中提出了一种基于非线性的横摇周期计算方法，通过该方法计算得到的横摇周期会随船舶横摇角的变化而发生改变。若将该方法运用到瘫船稳性第1 层薄弱性衡准中，不仅可以解决横摇周期计算方法的适用性问题，还可提高稳性校核的准确性。

本文将基于以上2 种横摇周期计算方法分别编写程序［5］，并选取渔船、油船、消防船等不同种类的24 艘样船共72 种载况进行计算，然后根据计算结果对比分析2 种计算方法的差异。

1 船舶横摇周期计算方法

1.1 瘫船稳性第1 层薄弱性衡准中的横摇周期计算方法

横摇周期是指船舶从左舷摇向右舷再回到左舷所经历的时间。在瘫船稳性第1 层薄弱性衡准中，使用固定公式（1）对横摇周期进行计算，该公式是基于70 余艘实船测试数据，由Morita 根据统计制定然后简化得到［6］。

式中：系数C=0.373+0.023(B d)-0.043(Lwl100)，其中d 为吃水，Lwl为水线长；B 为船宽；GM 为经自由液面修正后的初稳性高。

根据式（1），可以得到船舶在单一扰动力矩下的线性横摇幅频曲线，如图1 所示。从图中可以看出，船舶线性横摇频率nθ为定值，不随横摇角θ的变化而发生任何改变。图中，ω为波浪频率。

图1 线性横摇幅频曲线Fig.1 Linear rolling frequency-amplitude curve

瘫船稳性第1 层薄弱性衡准考虑的条件是船舶处于不规则波和阵风环境，但式（1）计算的是船舶在静水中且没有任何阻力影响情况下的线性横摇固有周期。在静水无阻力条件下，不需要考虑阻尼力矩和扰动力矩的影响，线性横摇，也即横摇角相对较小，复原力矩可采用公式D·GM·θ直接进行计算。根据牛顿第二定律，可建立如式（2）所示的单自由度线性横摇运动微分方程［7］。

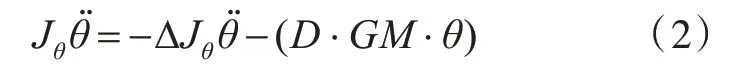
式中：θ̈为横摇角加速度；ΔJθθ̈为附加惯性力矩；D 为排水量。

假设全船质量（包括附加质量）集中于某一点，则该点距横摇轴的距离为横摇惯性半径，通过该半径，可相对容易地计算出船舶质量惯性矩Jθ+ΔJθ。对式（2）进行简单的推导后，便可得到现有横摇周期计算公式（1）。

若严格按照瘫船稳性第1 层薄弱性衡准中的环境条件，受不规则横浪等环境条件的影响，船舶横摇势必受到阻力作用，同时，考虑到横摇角度较大时复原力臂曲线的非线性特征，船舶势必会发生非线性横摇运动。因此，通过式（1）对横摇周期进行计算显然不够准确。

1.2 基于非线性的横摇周期计算修正方法

船舶做非线性横摇运动的主要原因是非线性的横摇复原力矩。如图2 所示，只有当横摇角度θ相对较小时复原力矩M 才与θ呈线性关系，即等于D·GM·θ。特别是对于代表大多数民用船舶的曲线3，线性假设与实际差别较大，使用现有方法对横摇周期进行计算会存在一定的误差，从而导致瘫船稳性失效模式的评估结果不够准确。

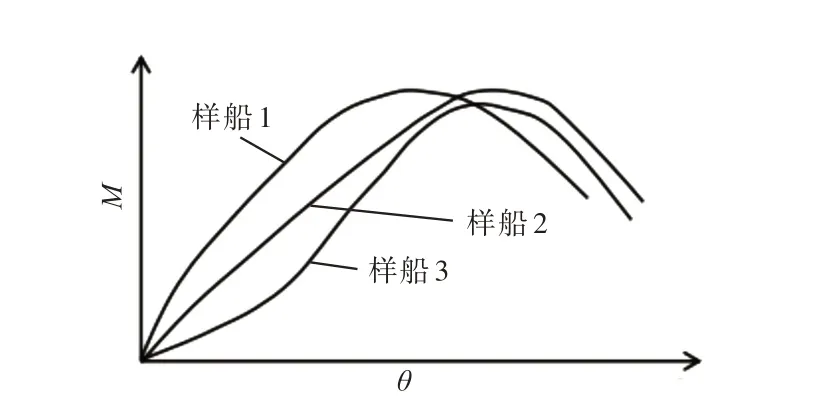
图2 不同种类船舶复原力臂曲线示意图Fig.2 Schematic diagram of the restoring armcurves with different types of ships

假设复原力矩取非线性关系-M=C1θ+C3θ3，则非线性横摇运动微分方程为

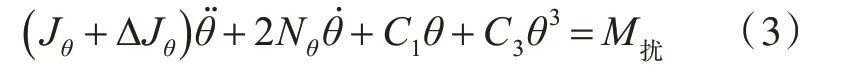
式中：Nθ为阻尼比例常数；C1，C3分别为复原力的线性和三次项系数；M扰为扰动力矩。通过数学推导，然后忽略高频部分，便可得到船舶发生非线性横摇运动时的横摇频率：

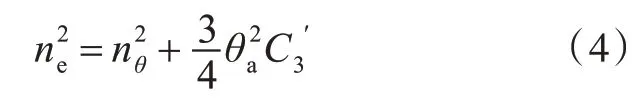
根据式（4），船舶非线性横摇频率ne不再是一个定值，而是横摇幅值θa的函数。船舶在单一扰动力矩下发生非线性横摇运动时的幅频曲线如图3 所示。从图中可以看出，幅频曲线分布在横摇频率曲线的两侧，且随着横摇频率曲线的偏斜，幅频曲线的峰区也会随之呈歪斜状。

图3 非线性横摇幅频曲线Fig.3 Nonlinear rolling frequency-amplitude curves

所以，经综合考虑非线性复原力矩曲线的形状以及横摇幅值等因素的影响，对于瘫船稳性第1层衡准中的横摇周期计算，建议采用SDC 5/6/8标准中的非线性方法［8］，即

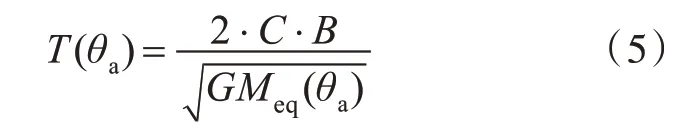
式中：T(θa) 为特定横摇幅值θa下的横摇周期；GMeq(θa)为特定横摇幅值θa下的等效初稳性高，其计算公式为

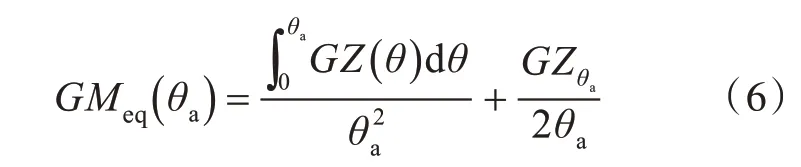
由式（5）和式（6）可知，0～θa范围内的切线平均斜率以及复原力臂GZ 曲线下的面积是影响船舶横摇周期计算结果的2 个主要因素。

2 横摇周期修正方法的验证与应用

波兰对7 艘样船共30 种载况进行了数值模拟，并基于影响横摇周期的主要因素提出了建议的横摇周期计算方法［8］。对比图1 和图3 可以发现，在非线性情况下，线性横摇频率nθ与幅频曲线的交点一定小于横摇幅值θa的某一点，而非线性横摇频率ne与幅频曲线的交点则为横摇幅值。

为了进一步对式（5）和式（6）进行验证，本文对3 艘不同种类的样船进行了计算，样船基本信息如表1 所示。

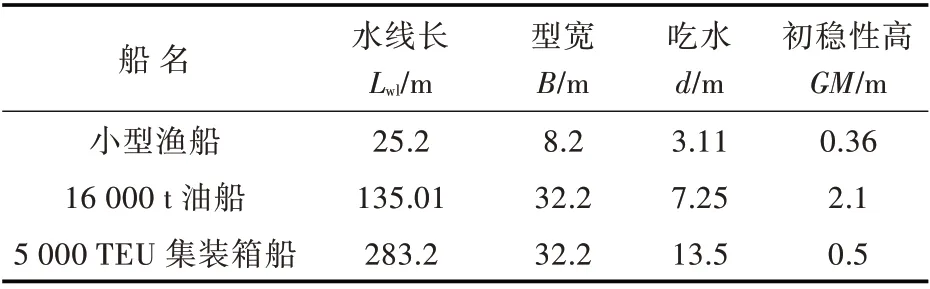
表1 样船基本信息Table 1 Basic information of sample ships

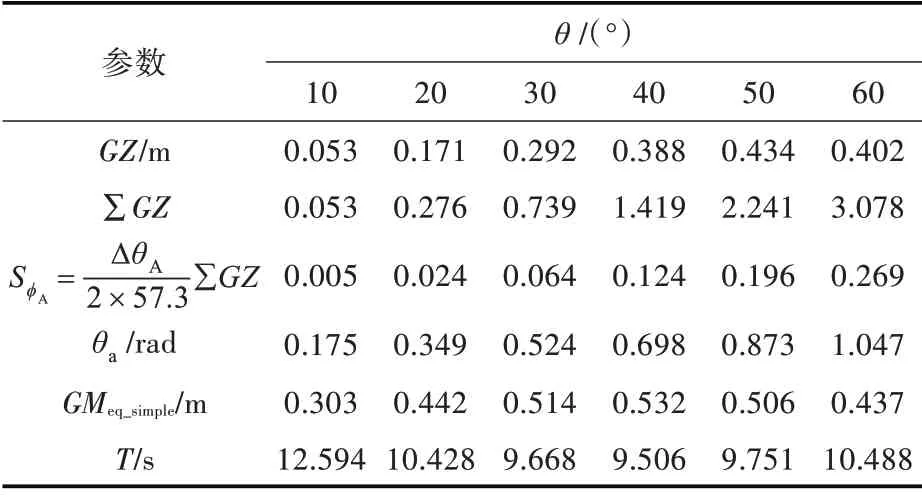
表2 小型渔船横摇周期简化计算方法Table 2 Simplified method for calculating rolling period of small fishing boat

3 艘样船的计算结果如图4～图6 所示。图中：GM 为基于现有方法计算得到的初稳性高；GMeq为基于修正方法，准确求得不同横摇角对应的初稳性高；GMeq_simple为基于修正方法，通过梯形法计算曲线面积而得到的不同横摇角对应的初稳性高。

由计算结果可知，GMeq与GMeq_simple基本重合，误差主要集中在10°～15°横摇角之间，这主要是由数值积分的梯形法则在每个区间进行线性性质的假设所导致。不过，在该横摇幅度范围内，船舶基本不会发生安全问题，所以通过近似方法计算船舶在不同横摇角下的横摇周期，其计算精度完全可以接受。

图4 小型渔船横摇周期计算结果对比Fig.4 Comparison of rolling period calculation results for small fishing boat

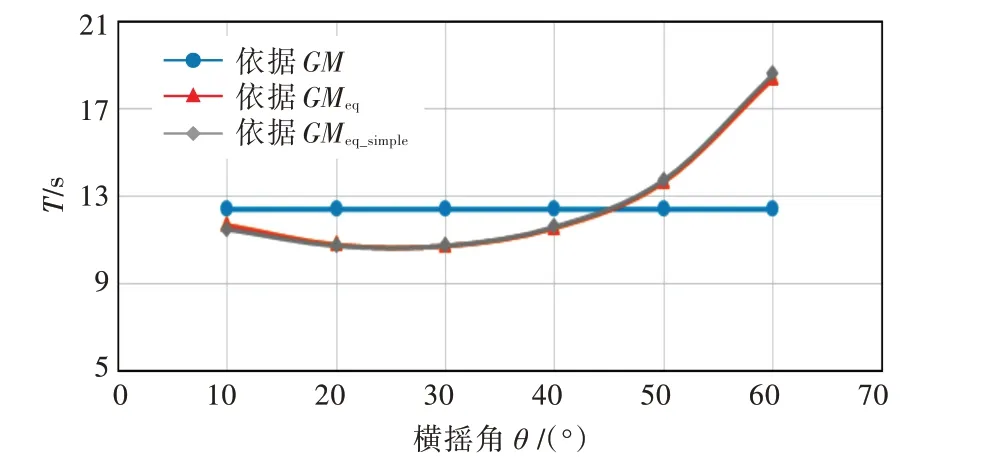
图5 16 000 t 油船横摇周期计算结果对比Fig.5 Comparison of rolling period calculation results for 16 000 t tanker

图6 5 000 TEU 集装箱船横摇周期计算结果对比Fig.6 Comparison of rolling period calculation results for 5 000 TEU container ship

采用IMO 现有方法计算得到的横摇周期与方法修正后的计算结果间确实存在一定的差异，该差异大小随横摇角的变化而有所不同。5 000 TEU 集装箱船的结果差异较为明显，当横摇角θ=40°时，通过两种方法计算得到的横摇周期相差8.5 s。

使用现有方法计算船舶横摇周期，一方面有可能使船舶在安全范围内没有意义地避开一个速度与航线的配置组合，另一方面还有可能出现因共振而导致大幅横摇的危险情况，这种情况在GZ曲线具有明显非线性特征的船上发生的概率较大，例如，船舶最大复原力臂位于25°～30°横摇角之间相对较小的区域范围内时。所以，使用修正方法代替现有计算方法不仅能准确得到船舶横摇周期，还能协助船舶操纵者制定安全、经济、高效的航线。

3 横摇周期计算方法对横摇幅值计算结果的影响

3.1 横摇幅值计算修正

使用修正的横摇周期计算方法替代目前的常用公式，不仅可以更加准确地反映谐摇条件，还将影响第2代完整稳性失效模式的薄弱性评估结果。

在瘫船稳性第1 层薄弱性衡准中，是通过式（7）来计算横摇幅值［9］：

式中，k，X1，X2，r均为系数。

根据《2008 年国际完整稳性规则》中的气象衡准，式（7）中的波陡s 需要根据船舶横摇周期插值确定，在6 ～30 s 的横摇周期范围内，横摇周期越大，波陡越小，且波陡范围为0.02～0.1。由式（1），根据经自由液面修正后的初稳性高，即可确定船舶横摇周期。

考虑非线性复原力臂曲线的影响后，横摇幅值θa与横摇周期T 之间具有特定的函数关系。同样是对式（7）进行求解，需要通过迭代来求解横摇幅值θa、横摇周期T 以及波陡s的值。根据式（5）和式（6），对瘫船稳性第1 层薄弱性衡准中的评估方法进行修改。假设船舶的初始横摇角θ0=10°，通过式（5）和式（6）计算初始横摇角θ0对应的横摇周期T1，得到船舶在横摇周期为T1时对应的波陡s1和横摇角θ1，然后按照该方法依次求得θ2，θ3，θ4……，当前、后两次迭代所得横摇角的差值小于10-4时，停止迭代，输出最终计算结果。

以航行中的24 m 渔政船为例，迭代过程如表3所示。表中：Sspecific为曲线下的面积；GZspecific为横摇角对应的复原力臂；GMspecific为等效初稳性高。经过8 次迭代后，得到了稳定的收敛结果。

表3 24 m 渔政船横摇幅值计算迭代过程Table 3 Iterative process for calculating roll amplitude of 24 m fishery administration ship

3.2 样船计算结果及分析

本文选取24 艘样船，每艘样船包含3 种载况，对72 种载况进行计算，其中包括船长较小的24 m渔船和船长较大的186 m 油船，以确保船长较大的跨度范围以及样船种类的多样性。分别通过2 种横摇周期计算方法对横摇幅值进行计算，计算结果按船长大小进行排序，如图7 所示。

图7 横摇幅值计算结果对比Fig.7 Comparison of rolling amplitude calculation results

根据计算结果可知，通过2 种方法计算得到的横摇幅值，其中71%的载况差值在0.5°范围内。不过也有空载出港的1 000 t 和2 000 t 油船、大型拖网渔船、6 400 方LNG 船、16 000 t 油船等部分载况计算结果的差值较大。其中，空载出港的1 000 t 油船的载况计算结果最为显著，差值几乎达5°。

根据式（7），横摇幅值是通过由横摇周期T 插值得到的波陡s进行计算的。因插值得到的波陡s变化范围较小，使得采用2 种方法计算得到的横摇幅值差异也不大，所以有必要输出横摇周期的计算结果以进行进一步的比较分析。

计算波陡s时，如果横摇周期小于6 s，波陡s将取0.1，其不会使横摇幅值发生改变。因此，对于横摇周期小于6 s 的船舶，将无法进行准确的数学迭代。所以，这里仅输出横摇周期大于6 s 的57种载况进行比较分析，计算结果如图8 所示。

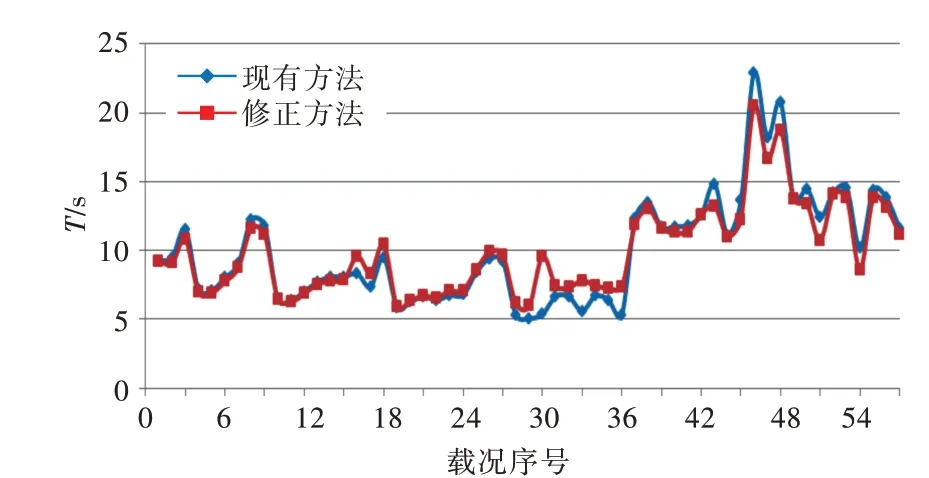
图8 横摇周期计算结果对比Fig.8 Comparison of rolling period calculation results

根据计算结果，通过2 种方法计算得到的横摇周期，有22.8%的载况其差值大于1 s，差异程度和横摇幅值相比更加明显，且对于横摇幅值计算结果差别较大的载况，其横摇周期计算结果的差别同样显著。

输出满载出港LS 300 t 渔政船以及空载出港1 000 t油船的GZ 曲线进行对比分析，其中LS 300 t渔政船采用现有方法和修正方法所得横摇周期计算结果相差0.17 s，几乎一致，而1 000 t 油船的横摇周期计算结果则相差4.2 s，差异较大。

如图9 所示，在0°到最大复原力臂对应的横摇角范围内，LS 300 t 渔政船的GZ 曲线线性特征明显，原点处的切线斜率，也即初稳性高为0.61 m，而本文建议使用的等效初稳性高计算结果为0.63 m，这样可以使横摇周期的计算结果几乎不变。

如图10 所示，空载出港1 000 t 油船最大复原力臂对应的横摇角θ≈25°，GZ 曲线非线性特点较为显著。原点处的切线斜率，也即初稳性高为13.363 m，而本文建议使用的等效初稳性高计算结果仅为4.193 m，相差3 倍，横摇周期计算结果相差较大。

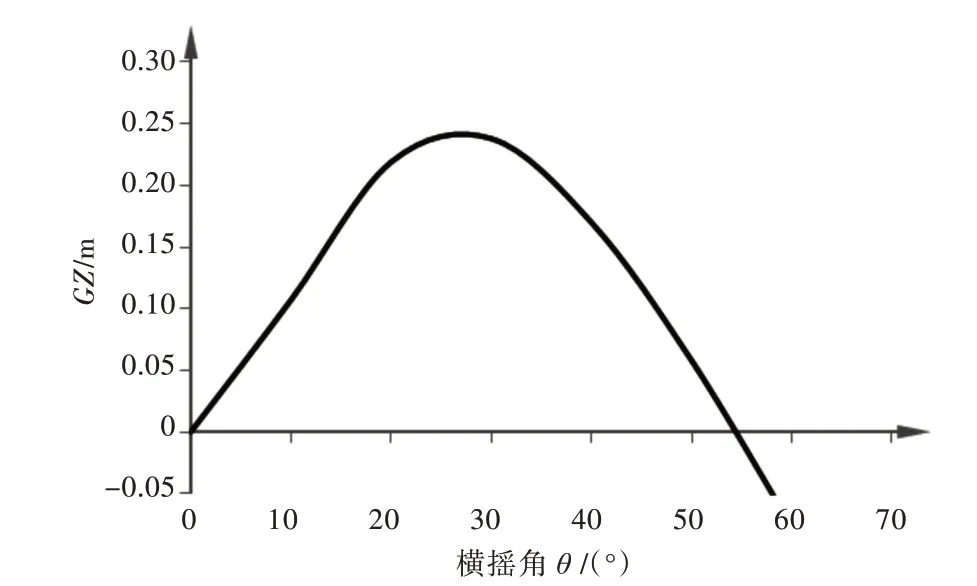
图9 LS 300 t油船满载出港GZ 曲线Fig.9 GZ curve of LS 300 t tanker in full loaded departure

图10 1 000 t油船空载出港GZ 曲线Fig.10 GZ curve of 1 000 t tanker in ballast departure

4 结 论

本文基于船舶运动微分方程，分析了现有横摇周期计算方法的缺陷与不足，并通过3 艘典型样船，验证了建议方法的准确性以及便捷性。基于2 种横摇周期计算方法编写对应的程序，对样船进行了计算，通过对综合计算结果的分析，得到如下几点结论：

1）通过原理分析以及样船计算，发现现有横摇周期计算方法没有考虑GZ 曲线的非线性影响，当船舶GZ 曲线的非线性特征明显时，使用现有方法计算得到的横摇周期不够准确，建议使用修正的横摇周期计算方法。

2）现有的横摇周期计算方法会影响瘫船稳性等失效模式薄弱性评估结果的准确性，建议使用修正的横摇周期计算方法，通过迭代来对横摇幅值进行计算。

3）船舶在海面上航行时，利用修正的横摇周期计算方法可以更加准确地计算船舶处于不同横摇角所对应的横摇周期。