绝对法齿距偏差测量中回转误差的影响及补偿

摘  要：文章针对转台回转误差在对采用绝对法进行齿轮齿距累计偏差测量中的影响进行了理论研究及实验验证。首先建立了回转误差对绝对法齿距累计偏差测量影响的数学模型，依据该数学模型推导出回转误差在齿距累计偏差测量方向的映射系数以及左右齿面齿距累计偏差计算时的回转误差的补偿公式。接着探讨了齿轮分度圆大小和测头测球半径大小对回转误差映射系数的影响。最后对误差补偿的效果進行仿真实验的验证，仿真实验结果表明文章所提出的补偿方法可以有效降低转台径向回转误差对测量结果的影响。

关键词：误差补偿;回转误差;齿距累积偏差;绝对法测量;齿轮测量

中图分类号：TG86      文献标识码：A 文章编号：2096-4706（2020）24-0160-04

Influence and Compensation of Rotation Error in Absolute Method Pitch

Deviation Measurement

HUANG Feiyao

（Xian Technological University，Xian  710021，China）

Abstract：In this paper，the influence of the rotation error of the turntable on the measurement of the cumulative deviation of gear pitch by the absolute method is studied theoretically and verified experimentally. Firstly，the mathematical model of the influence of the rotation error on the measurement of the absolute method pitch cumulative error is established. Based on the mathematical model，the mapping coefficient of the rotation error in the measurement direction of the cumulative pitch error and the compensation formula of the rotation error in the calculation of the cumulative pitch error of the left and right tooth surfaces and pitch are deduced. Then the influence of the size of the gear indexing circle and the radius of the probe measuring ball on the mapping coefficient of the rotation error is discussed. Finally，the effect of error compensation is verified by simulation experiment. The simulation experiment results show that the proposed compensation method can effectively reduce the influence of the radial rotation error of the turntable on the measurement results.

Keywords：error compensation;rotation error;pitch accumulated deviation;absolute method measurement;gear measurement

0  引  言

齿轮是典型的标准化传动零件，广泛应用于机器设备、航空航天、仪器仪表以及军工等领域[1]。齿距偏差是齿轮重要的精度指标，其偏差值会影响齿轮的平稳性[2]。目前高精度齿轮的齿距偏差大多使用齿轮测量中心、坐标测量机等仪器进行测量[3-5]。

在进行齿轮齿距测量时，为了提高齿轮齿距偏差的测量精度，国内外专家学者对影响齿轮齿距偏差测量的因素展开了大量的研究。大连理工大学娄志峰等针对提高齿距偏差测量精度从测量方法、测量点位置等多方面进行研究并取得了一定成果[6，7]。西安工业大学卢春霞等分析了齿轮安装偏心对齿距偏差测量的影响，杨燕鸽[8]等提出齿距累积误差的安装偏心补偿模型，分析偏心的幅值和相位角对补偿测量结果的影响。

综上所述，大部分专家学者研究齿轮齿距偏差测量时，主要是从齿轮齿距测量的齿轮安装偏心误差、系统误差等方面进行研究分析。转台回转误差属于系统误差的一部分，既包括一次谐波分量即偏心误差，还包括多次谐波分量即长周期误差与短周期误差。转台回转误差对齿距偏差测量影响的研究相对于偏心误差对齿距偏差测量影响更加深入全面。统计发现，高精密测量仪器工作回转台的回转误差对齿轮齿距偏差测量的影响研究很少。本文主要研究绝对法齿轮齿距偏差测量中，回转误差对齿距偏差测量影响的理论分析和实验研究。建立回转误差与齿距偏差的映射关系，根据映射关系对齿距累计偏差进行补偿并通过仿真及和测量实验进行验证。

1  转台回转误差对绝对法齿距偏差测量影响的数学模型

转台回转误差对绝对法齿距偏差测量的影响如图1所示，假设齿轮没有齿形误差且无表面形貌误差，则转台回转误差可以分解为X方向的跳动、Y方向的跳动。转台回转误差X、Y两个方向的跳动都会影响绝对法齿距偏差测量的结果。以齿轮的回转中心为原点O、以水平向右为X轴建立测量坐标系。假设测头没有定位误差，即测头测球中心0P位于分度圆与X轴的交线处，且测头的测杆与X轴重合，即测头的敏感方向与Y轴平行。在考虑测头的半径情况下，实际测量中测量圆位置与理想测量圆（分度圆）位置不重合，实际接触点为C，同时X向跳动与测头敏感方向垂直，Y向跳动与测头敏感方向平行，所以必须将测量得到转台回转误差映射到实际测量圆的测量方向上，然后映射到齿距的评价方向也就是测量圆的切线方向。

根据数学模型几何关系在直角三角形OTOP和直角三角形OTC中，可得实际测量圆上的压力角αk为：

（1）

其中，r为被测齿轮分度圆半径，rb为被测齿轮基圆半径，rp为测球半径。

将转台回转误差X向跳动先映射到测头的敏感方向然后映射到齿距偏差评价方向上，可得出X向跳动的映射系数kx为：

（2）

其中，α为齿轮压力角，?X为X方向回转误差大小值。

与X向映射系数同理可得转台回转误差Y向跳动在齿距偏差实际测量方向的映射系数ky为：

（3）

其中，?Y为Y方向回转误差大小值。

根据上述径向回转误差推导出回转误差对齿距累计偏差的误差补偿公式，左齿面齿距偏差的误差补偿公式为：

（4）

其中，L为左向，FP1为实际测量齿距累计偏差值，为FLpk补偿后左齿面齿距累计偏差值。

与左齿面测量齿距偏差不同的是在进行右齿面齿距偏差测量时测头的压入量与左齿面测量时相反，所以右齿面齿距偏差的补偿公式为：

（5）

其中，R为右向，Fp2为实际测量齿距累计偏差值，FRpk为补偿后右齿面齿距累计偏差值。

从上面公式可知，回转误差X向补偿系数与Y向补偿系数都和被测齿轮分度圆半径与测头半径的大小有关。

2  讨论分析

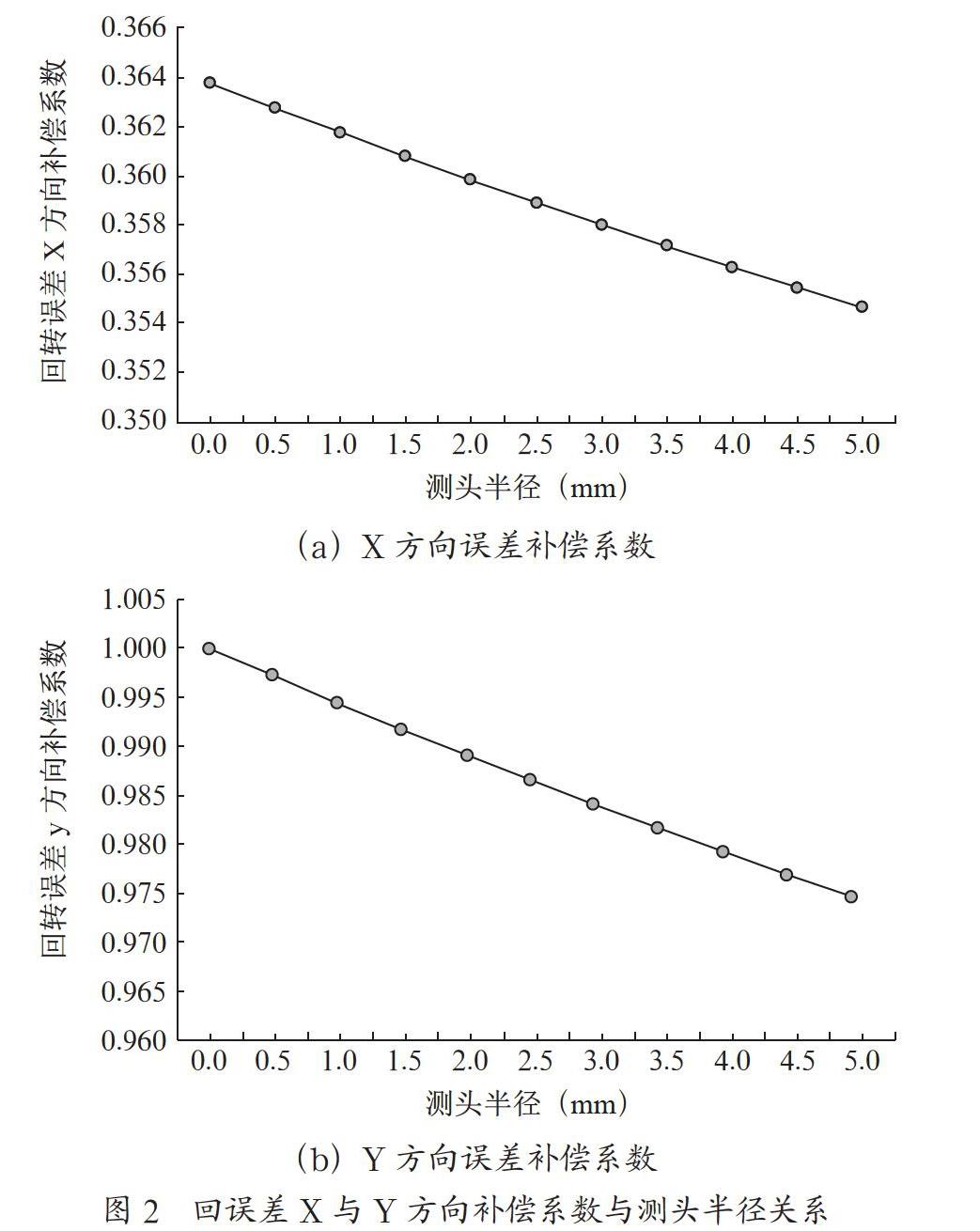
固定被测齿轮分度圆半径，研究测头半径大小变化对回转误差X与Y方向误差补偿系数影响的趋势。以r=60 mm的标准齿轮为例，则回转误差X与Y方向误差补偿系数随测头半径变化趋势如图2所示。

从图2中可以明显地看出，将测头球心固定在被测齿轮分度圆上时，X与Y方向误差补偿系数大小会随着测头半径增大而减小。当不考虑测头半径时，Y方向误差补偿系数最大，对测量的影响将会为1：1。

固定测头半径，研究被测齿轮分度圆半径变化对回转误差X与Y方向误差补偿系数的影响趋势。以测头半径1 mm为例，则回转误差X与Y方向误差误差补偿系数随被测齿轮分度圆半径变化趋势如图3所示。

从图3中可以看出回转误差X与Y方向误差补偿系数随着被测齿轮分度圆的增加而非线性的增加。当齿轮分度圆半径达到一定大的值时，回转误差X与Y方向补偿系数将无限接近于固定值。

3  实验验证

在MATLAB中进行仿真实验验证，采用绝对法进行标准齿轮（m=4，z=30，其中m为齿轮模数）齿距累计偏差测量，齿距累计总偏差理论值为20 μm。加入简谐类型回转误差情况下采用绝对法进行齿轮齿距偏差测量，测量圈数为1圈。齿距累计偏差的发生函数为：

（6）

其中，z为齿轮齿数，i为齿序。

回转误差（X与Y向跳动相同）发生函数为：

（7）

其中，z为齿轮齿数，k为齿序。

对仿真实验结果按照式（4）、式（5）分別对左右齿面齿距累计偏差进行补偿，并与理论值进行比较验证补偿效果。左右齿面齿距累计偏差补偿前后结果如图4和表1所示。

表1可以看出，在补偿前，回转误差造成的绝对测量左右齿面齿距累积偏差值达到了21.52 μm和23.68 μm，说明回转误差对于齿距累积偏差的测量有非常显著的影响。在利用补偿公式（6）和式（7）对回转误进行补偿后，测量结果的结果误差分别降到了0.04 μm和0.01 μm，基本消除了回转误差对齿距偏差测量的影响，证明了误差补偿公式（6）和式（7）的正确性。补偿后的误差值与理论值并不完全相符，这是可能是由于理论值是连续的，测量值是离散的可能取值没有到峰值。

从图4可以看出，补偿前各个齿的齿距累积偏差与理论齿距偏差曲线在幅值和相位上存在较大差别，单个齿的最大误差在1齿上达到3.07 μm，这是回转误差中长周期误差与整周误差造成的。补偿后齿距累积偏差曲线和理论齿距累计偏差曲线基本一致，单个齿的最大误差为0.30 μm，发生在6个齿，说明该齿可能在峰值附近没有取到峰值而导致误差最大。

4  结  论

为了提高齿轮齿距偏差测量精度，本文主要针对转台回转误差对绝对法齿距偏差测量的影响进行了理论分析及仿真验证，可以得出以下结论：

（1）通过建立回转误差对齿距偏差测量影响的数学模型，定义了回转误差X和Y方向的误差影响系数，揭示了转台回转误差对齿距累积偏差测量影响的大小关系。

（2）讨论了X与Y方向回转误差影响系数大小与测头测球半径和被测齿轮分度圆大小的关系。研究发现：X与Y方向回转误差影响系数随着测头测球半径的增加而减小，随着被测齿轮分度圆半径的增大而增大，但总体影响不大

（3）通过数值仿真验证了转台回转误差对齿距偏差测量影响的数学模型的正确性，经过补偿后的齿距累计总偏差相对于补偿前的齿距累计总偏差与仿真结果基本保持一致，说明该补偿有效可行。

本文建立了转台回转误差对齿轮齿距偏差测量影响的数学模型和误差补偿模型，相比于现有文献，该模型不但反映了齿轮综合偏心的影响，还反映了回转误差中长周期误差和短周期误差的影响，深化了对于回转误差与齿距偏差测量之间关系的认识。通过误差补偿模型能够有效地减小转台回转误差对齿轮齿距累积偏差测量的影响，对于提高齿轮齿距偏差的测量精度具有一定的实用价值。文中不足在于仅仅考虑了回转误差中径向回转误差对齿距偏差测量的影响，没有考虑倾角摆动误差对齿距偏差测量的影响，后续将对此展开研究。

参考文献：

[1] 魏建杰，汤洁，石照耀.基于ISO 1328-1：2013的齿距偏差评定方法 [J].测控技术，2019，38（9）：88-91.

[2] 郭宝余，娄志峰，高立嵩，等.齿轮全齿面偏差的拟合及分离技术 [J].机械传动，2014，38（10）：114-116+130.

[3] 高立嵩，娄志峰，马勇.一种新型齿距偏差评价方法研究 [J].机械设计与制造，2015（11）：18-20.

[4] 凌四营，王立鼎，娄志峰，等.超精密齿距偏差测量中测点位置的误差补偿 [J].仪器仪表学报，2014，35（3）：691-696.

[5] 娄志峰，贺海钊，凌四营，等.齿距偏差测量中系统误差的分离方法 [J].纳米技术与精密工程，2012，10（6）：537-540.

[6] 宋洪侠，赵苏苏，娄志峰，等.降低齿轮齿距累积偏差的方法 [J].光学精密工程，2012，20（8）：1796-1801.

[7] 王立鼎，凌四营，马勇，等.精密、超精密圆柱渐开线齿轮的加工方法 [J].光学精密工程，2009，17（2）：321-326.

[8] 杨燕鸽，王建华.齿轮安装偏心情况下齿距误差测量精度分析 [J].工具技术，2008（2）：70-72.

作者简介：黄飞耀（1991—），男，汉族，陕西省渭南人，硕士研究生在读，研究方向：计算机辅助精密测量。