中考数学动态几何题静态化思考

摘 要：本文通过对2014年质检题及近几年中考试题中的动态几何题的分析，研究对策，寻找变化中图形的性质和特征，抓住变化图形中的不变量，化动为静，发现规律，培养学生解题素养。

关键词：初中数学;动态几何题;静态思考

运动与变化是动态观，在解数学问题尤其是几何图形问题时，经常要用这种观念来审视或分析问题，这其实就是解题的辩证观，因为运动与静止，固定与变化等，既对立又统一，我们利用这种对立统一就能使问题易于解决，对培养思维的灵活性很有好处，二期课改后数学中的压轴题逐步向数形结合，动态几何、动手操作、实验探究等方向发展，题意创新，目的是考查学生分析问题，解决问题的能力，特别是动态几何，让考生感到特别烦恼，我们教师必须在教学中研究对策，把握方向，让动态中的数学转向静态中思考，更好的培养学生解题素养，本文就今年龙岩质检题及历年各地中考题谈谈自己的观点。

一、 点在线上运动问题

（2014年龙岩质检题20）（如图）在△ABC中，点D、E分别在边BC、AC上，连结AD、ED，且∠1=∠B=∠C。

（1）请找出图中一对相似三角形：______________________。

（2）若AE=3，EC=2，求线段的AD的长（精确到0.01）。

本题是在新教材九年级上《相似形》的改编，典型的一线三角（三等角）的问题。该题几乎未提动点问题，其实质上是动态几何问题，在∠1=∠B=∠C的条件上，点D在线段BC上运动，从而带动了点E在线段AC上运动，在整个运动过程中，△ABD，△ADE，△DEC，△ADC中的其中两个角都一直在变化中，因此就不能再去确定另一组角相等，此时我们必须在运动中寻找相对的静态量，不难发现∠DAE（∠CAD）是△CAD和△DAE的公共角，虽然点D在BC上运动时，这个公共角也在变化之中，但始终是一个等量，从而得到△DAE∽△CAD。

（2014年龙岩质检题24）（如图）将一块三角板放在边长为1的正方形ABCD上，并使它的直角顶点P在对角线AC上滑动，一直角边始终经过点B，另一直角边与射线DC相交于点Q，设AP=x。

（1）当点Q在边CD上时，线段PQ与线段PB有怎样的数量关系？试证明你观察得到的结论。

（2）是否存在点P（P不与A重合），使△PCQ为等腰三角形？若存在，请求出相应的x的值;若不存在，请说明理由。

（3）设以点B，C，P，Q为顶点的多边形的面积为y，试确定y与x之间的出发关系式。

此考题可以从三个方面去入手：

方案（一）：过点P作PM⊥AB，PN⊥DC，垂足分别为M，N（此时M，N，P三点共线），由于点P在AC上滑动，线段PB，PQ长度也随之发生了变化，此时必须在动中寻静，在整个运动的过程中，正方形ABCD和三角板EPF始终不会发生变化，即∠FPE都为直角，从而恒有∠1+∠2=90°也就可得∠MBP=∠2，∠1=∠NQP的结论（静态量），还有由正方形的性质也可得到△AMP和△CNP也是等腰直角三角形，虽然等腰三角形大小会随点P的运动发生变化，但其形状不变，因此也就容易得到的结论（静态量）从而证得△BMP≌△PNQ。

方案（二）：过点P作PM⊥BC，PN⊥DC，由于线段AC是正方形ABCD的对角线，不论P点在线段AC上如何运动，四边形PNCM都为正方形，始终都有∠MPN=90°。又因为∠EFP始终也是直角，即∠1+∠MPQ=∠2+∠MPQ=90°从而得到∠1=∠2的结论（静态量），易证得△PNQ≌△PMB即PB=PQ。

方案（三）：本题由于没有说明点P不能与点A重合，①当点P与A重合时，PB=AB，PQ=AD，容易得到PQ=PB，②当点P与线段AC的中点O重合时，PB=OB，PQ=OC此时也可得到PQ=PB，但我们不能以特殊情况去说明一般性的结论，当点P滑动到线段AC的中点之前，

都恒有∠FPE=∠BCD=90°（静态量），在四边形BFGC中都存在着∠BPQ+∠BCQ=180°，从而构成了以BQ为直径，P，Q，C，B，四点共圆，再由正方形的性质可得∠1=∠2=45°，即PQ，PB所对的劣弧都为45°的弧（同圆中等弧对等弦）证得PQ=PB。

二、 绕定点旋转的问题

研究历年来各地区的动态几何压轴试题，就能明确中考数学试题热点的形成和命题的动向，在素质教育的背景下更明确地体现新课程标准的导向，动态几何题最突出的特点就是图形是运动的，变化的，解决动态问题时：首先需要把动态问题静态化，化为几个静态的过程，“以静制动”抓住变化中的“不变量”以不变应万变。

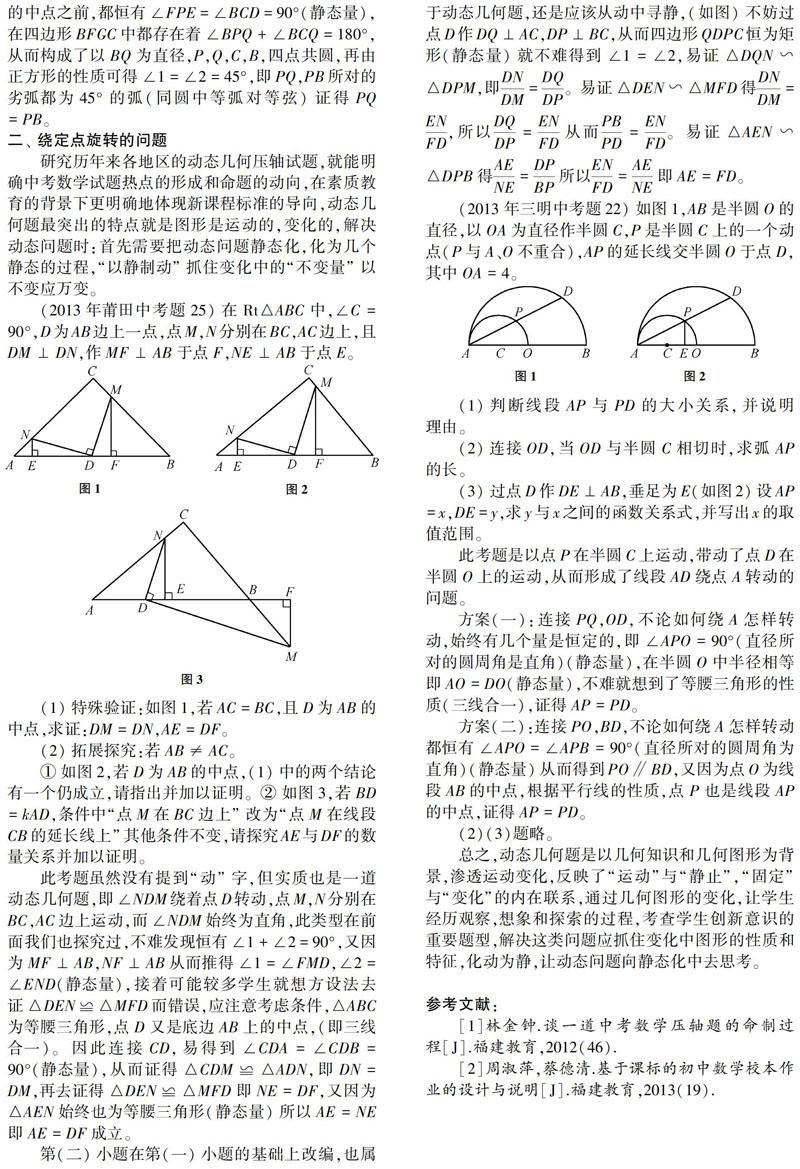
（2013年莆田中考题25）在Rt△ABC中，∠C=90°，D为AB边上一点，点M，N分别在BC，AC边上，且DM⊥DN，作MF⊥AB于点F，NE⊥AB于点E。

（1）特殊验证：如图1，若AC=BC，且D为AB的中点，求证：DM=DN，AE=DF。

（2）拓展探究：若AB≠AC。

①如图2，若D为AB的中点，（1）中的两个结论有一个仍成立，请指出并加以证明。②如图3，若BD=kAD，条件中“点M在BC边上”改为“点M在线段CB的延长线上”其他条件不变，请探究AE与DF的数量关系并加以证明。

此考题虽然没有提到“动”字，但实质也是一道动态几何题，即∠NDM绕着点D转动，点M，N分别在BC，AC边上运动，而∠NDM始终为直角，此类型在前面我们也探究过，不难发现恒有∠1+∠2=90°，又因为MF⊥AB，NF⊥AB从而推得∠1=∠FMD，∠2=∠END（静态量），接着可能較多学生就想方设法去证△DEN≌△MFD而错误，应注意考虑条件，△ABC为等腰三角形，点D又是底边AB上的中点，（即三线合一）。因此连接CD，易得到∠CDA=∠CDB=90°（静态量），从而证得△CDM≌△ADN，即DN=DM，再去证得△DEN≌△MFD即NE=DF，又因为△AEN始终也为等腰三角形（静态量）所以AE=NE即AE=DF成立。

第（二）小题在第（一）小题的基础上改编，也属于动态几何题，还是应该从动中寻静，（如图）不妨过点D作DQ⊥AC，DP⊥BC，从而四边形QDPC恒为矩形（静态量）就不难得到∠1=∠2，易证△DQN∽△DPM，即DNDM=DQDP。易证△DEN∽△MFD得DNDM=ENFD，所以DQDP=ENFD从而PBPD=ENFD。易证

△AEN∽△DPB得AENE=DPBP所以ENFD=AENE即AE=FD。

（2013年三明中考题22）如图1，AB是半圆O的直径，以OA为直径作半圆C，P是半圆C上的一个动点（P与A、O不重合），AP的延长线交半圆O于点D，其中OA=4。

（1）判断线段AP与PD的大小关系，并说明理由。

（2）连接OD，当OD与半圆C相切时，求弧AP的长。

（3）过点D作DE⊥AB，垂足为E（如图2）设AP=x，DE=y，求y与x之间的函数关系式，并写出x的取值范围。

此考题是以点P在半圆C上运动，带动了点D在半圆O上的运动，从而形成了线段AD绕点A转动的问题。

方案（一）：连接PQ，OD，不论如何绕A怎样转动，始终有几个量是恒定的，即∠APO=90°（直径所对的圆周角是直角）（静态量），在半圆O中半径相等即AO=DO（静态量），不难就想到了等腰三角形的性质（三线合一），证得AP=PD。

方案（二）：连接PO，BD，不论如何绕A怎样转动都恒有∠APO=∠APB=90°（直径所对的圆周角为直角）（静态量）从而得到PO∥BD，又因为点O为线段AB的中点，根据平行线的性质，点P也是线段AP的中点，证得AP=PD。

（2）（3）题略。

总之，动态几何题是以几何知识和几何图形为背景，渗透运动变化，反映了“运动”与“静止”，“固定”与“变化”的内在联系，通过几何图形的变化，让学生经历观察，想象和探索的过程，考查学生创新意识的重要题型，解决这类问题应抓住变化中图形的性质和特征，化动为静，让动态问题向静态化中去思考。

参考文献：

[1]林金钟.谈一道中考数学压轴题的命制过程[J].福建教育，2012（46）.

[2]周淑萍，蔡德清.基于课标的初中數学校本作业的设计与说明[J].福建教育，2013（19）.

作者简介：黄德辉，福建省漳平市，福建省漳平第三中学。