Abaqus粘结接触模型在锚杆抗拔试验中的应用研究
孙子跃,陈小丹
(1.东莞市水务技术中心,广东 东莞 523000;(2.广东省水利水电科学研究院,广东 广州 510635)
锚杆根据其受力状态的不同可分为:拉力型锚杆、压力型锚杆、荷载分散型锚杆(包括拉力分散型、压力分散型以及拉压分散型)。其中,拉力型锚杆相比于其他几种形式锚杆而言,其设计方法与施工技术较为成熟,是目前我国应用最为广泛的锚杆形式[1-2]。
拉力型锚杆受拉拔作用时,受力状态如图1所示。在拉拔力作用下,杆体(钢筋)受向上拉力,因杆体与注浆体(水泥)之间存在粘结力,为了保持位移协调,注浆体会对杆体产生向下的侧阻力。杆体在向上的拉拔力与向下的侧阻力作用下保持平衡。对于注浆体而言,同样的道理,土体将会对其产生向下的侧阻力,注浆体在杆体对其向上的侧阻力与土体对其向下的侧阻力的共同作用下保持平衡。杆体受到的拉拔力就通过三者之间的粘结作用传递到了土体中。然而,当杆体受到的拉拔力进一步增加时,杆体与注浆体或者注浆体与土体间的剪应力超过材料间的抗剪强度时,则会产生较大的相对位移,材料间的侧阻力表现为摩擦力。一般情况下,常规锚杆受拉拔作用时,相对杆体与注浆体间的粘结而言,注浆体与土体间的粘结往往先破坏转化为滑动摩擦力。传统的拉力集中型锚杆锚固段注浆体与土体间的粘结应力分布是很不均匀的,随着锚杆荷载的增加,锚杆锚固段粘结应力峰值逐渐由前端向根部转移,并出现渐进性破坏(如图1所示)。

图1 拉力型锚杆受力示意
目前,在对含有拉力型锚杆的支护工程(边坡、基坑)进行数值模拟分析其稳定性时,通常将锚固体与土体间的接触设为罚接触(Penalty contact),即计算位置处的接触剪应力τ=σtanφ,σ为计算点处的正应力,φ为摩擦角,这与实际情况截然不符。实际工程中,锚固体与土体间存在粘结作用,即使计算点处的正应力为零,抗剪强度仍然能达到其粘结强度,这种接触面间的粘结强度类似于土体本身的粘聚力c值。本文通过一抗浮锚杆的实际案例,探讨Abaqus中的粘结接触本构模型在拉力型锚杆受力分析中的合理性,以期能够推广到边坡、基坑等工程的安全性分析中,为设计施工提供依据。
1 工程概况与数值模型的建立
珠三角某水利工程采用拉力型锚杆抗浮,成孔直径150 mm,锚杆杆体为2根Ф32的钢筋,长度为33 m,抗拔承载力设计值为250 kN。为研究锚杆受力时的轴力分布,施工前在3根锚杆上(编号分别为11#、13#、22#)距顶部8 m、16.8 m、25.4 m以及29 m处安设应变片,待龄期达到要求后分别进行拉拔力为500 kN(设计值的2倍)的验收试验,试验结果与下文的数值计算结果一同绘制。
采用有限元数值软件Abaqus对上述拉力型锚杆抗拔试验进行模拟计算,为了考虑拉拔试验中锚杆受力时对周围土体的影响,模型中土体尺寸定为宽×高=40 m×40 m。现场土层分布较为复杂,至上而下包括素填土、粉土以及砂砾岩(强风化、微风化),其中厚度较大的粉土与砂砾岩对锚杆受力特性影响较大,在模型中将土层沿深度方向简化为24.8 m的粉土与15.2 m的强风化砂砾岩。锚固体尺寸定为Φ×H=0.15 m×33 m;为了简化计算,在模型中将2根Φ32的钢筋杆体等效为1根Φ45的钢筋(等面积)用于计算,则模型中钢筋杆体尺寸为Φ×H=0.045 m×33 m。模型示意如图2所示,网格划分如图3所示,锚固体局部如图4所示。

图2 数值模型示意

图4 锚头局部示意
为了使计算容易收敛,该模型中土体与锚固体的单元类型都采用二维4节点双线性四边形缩减积分平面应变单元CPE4R,杆体单元类型采用2节点线性二维杆单元T2D2。整个模型由7 790个土体单元、264个锚固体单元以及66个杆体单元组成。
模型中土体被假定为弹塑性材料,本构模型选用较为常用且容易收敛的摩尔-库伦模型,不同的土体对应的模型参数如表1所示;杆体与锚固体模型参数如表2所示。

表1 土体模型参数及取值
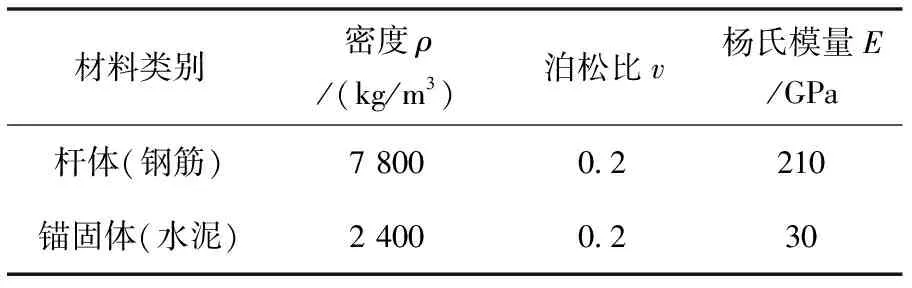
表2 杆体与锚固体模型参数及取值
因抗拔试验中,相比于锚固体与土体之间的相对位移而言,锚固体与杆体之间的相对位移是非常小的[3-4],故在本模型中锚固体与杆体之间的接触模型采用embedded(嵌入式)。另外,对于锚固体与土体间的接触而言,考虑实际情况中锚固体与土体间存在一个由水泥逐渐过渡到土的过渡区域,该区域材料属性介于水泥与土之间,在一定程度上类似于水泥土,即在力学行为上存在不容忽视的粘聚力,为了模拟过渡区域的这一粘聚力及其对整个受力体系的影响,在本模型中锚固体与土体之间的接触本构关系采用了粘结接触(cohesive behavior)。粘结接触本构关系应力应变曲线如图5所示。

图5 粘结接触本构关系示意
可以看出,粘结接触的应力应变关系曲线由损伤前的弹性阶段和达到损伤临界应力σ1后的损伤阶段两个阶段组成,为了简化计算,假设损伤阶段应力应变关系曲线为直线。该粘结接触本构有3个模型参数:σ1、ε1以及ε2,其中σ1为损伤临界应力,即开始损伤时的应力,ε1为开始损伤时的应变,ε2为完全损伤(破坏)时的应变。根据锚固体与土体的力学性质,将其具体接触参数确定为如下取值(见表3所示)。
模型边界条件:约束土体下边界的竖向位移与水平位移;约束土体两侧边界水平位移。

表3 粘结接触模型参数及取值
计算分为两个步骤:① 地应力平衡;② 锚杆抗拔试验分析。地应力平衡计算类型采用常规静态分析(Static,General),土体及锚固体的重力以体力(Body Force)的形式加载到模型中。锚杆抗拔试验分析计算类型也采用常规静态分析(Static,General),施加在锚杆上的荷载采用与现场试验相同的分级加卸载方式进行模拟。
2 计算结果与分析
地应力平衡计算结果如图6所示,其中(a)为土体竖向应力分布云图,(b)为土体竖向位移分布云图。

(a)土体竖向应力σy分布云图(单位:Pa)

(b)土体竖向位移Uy分布云图(单位:m)
从图6中可以看出,地应力平衡后,模型计算得出的土体竖向应力分布与理论值基本吻合。例如,在深度40 m处,模型计算竖向应力为772.3 kPa,理论值为1 800 kg/m3×10 N/kg×24.8 m+2 200 kg/m3×10 N/kg×15.2 m=780.8 kPa,二者十分接近。从图6(b)可以看出,地应力平衡后,模型表层土体竖向位移为0.36 mm,其量级基本满足地应力平衡精度要求。
地应力平衡后,按照现场试验的加卸载方式,在杆体顶部节点分级施加拉拔荷载直至500 kN,再分级卸载至0 kN。为了分析抗拔试验中锚杆受力时对周边土体的影响,以荷载为500 kN时为例,整个受力体系位移场示意如图7所示,锚头及周边土体局部位移如图8所示,为了能够直观地看到位移分布,图中的显示比例放大了50倍。

图7 荷载500 kN时的位移场示意

图8 锚头及周边土体局部位移示意
可以看出,当荷载为500 kN时,整个受力体系最大位移发生在锚头处,其值为8.77 mm。周边土体位移以锚头为中心向上及两侧发展,并随着深度及水平距离的增大而逐渐减小,在深度10 m或者水平距离7 m处,土体位移值小于1 mm。整个受力系统的位移没有突变之处,土体保持稳定,没有产生整体破坏与局部破坏。
将计算得到的各分级荷载作用下对应的锚头位移关系曲线绘制如图9所示,为了对比,试验11#、13#、22#锚杆的实际测量数据也一同表示在图9中。可以看出,模型计算曲线加载段,锚头位移随着荷载的不断加大而均匀增大,后一级荷载产生的位移量均小于前一级荷载产生的位移量的2倍,在最大荷载500 kN时锚头位移达到最大值8.77 mm。计算曲线卸载段锚头回弹位移随着荷载的减小而均匀减小,卸载至0 kN时,锚杆位移达到稳定,残余位移为3.5 mm,锚头位移回弹率为60.1%。可见,模型加卸载计算曲线呈现出与试验曲线相同的规律。另外,从图9中也可看出,二者在数值上也较为接近。例如,荷载为500 kN时,模型计算位移值为8.77 mm,位于12.34 mm(11#)与7.98 mm(13#)、7.76 mm(22#)之间,模型计算得到的p~s曲线与试验值较为吻合。
为了考察锚杆轴力分布随深度的变化规律,以荷载为500 kN时为例作简要分析,将其轴力分布绘制如图10所示,为了对比,现场3根锚杆的试验值也标注在图10中。

图9 荷载—位移关系曲线对比示意

图10 锚杆轴力分布对比示意
可以看出,模型计算得到的锚杆轴力随着深度的增加而逐渐减小,不是均匀分布。由于试验中锚杆应变片布置点较少,且只有深度为8 m处的测点有测值,其余3个测点(16.8 m、25.4 m、29 m)处的测值均为0,故模型计算得到的轴力分布与试验值只能作较为粗略的对比。深度为0 m处,即施加荷载处,模型计算得锚杆轴力为500 kN;深度为8 m处,模型计算结果为72.6 kN,位于试验测值96 kN(11#)与45 kN(13#)、46 kN(22#)之间;在深度为16.8 m处,模型计算结果为16.2 kN,而在这个深度3根锚杆的试验测值都已为0 kN,二者存在一定的偏差;另外,模型计算曲线轴力为0 kN所对应的深度为21 m,这与实际情况也略有相差。但总的来说,模型计算得到的内力分布基本能够反映锚杆实际受力情况,即锚杆受张拉荷载时,锚杆上部产生应力集中,超过一定深度的锚固段并不受力。所以说在工程应用中,锚杆长度有一个合理的有效值,单纯的追求增加锚杆长度会造成不必要的浪费,国内外许多研究中也同样提到了这一点[5-7]。
从上述对比分析可知,锚杆抗拔试验数值模拟结果与现场试验能较好地吻合,在一定程度上能反映出锚杆受力时的力学响应及对周边土体的影响,验证了粘结接触模型的适用性。在实际工程应用中,能够在确定锚杆合理长度及周边位移控制等方面提供依据。
3 结语
在Abaqus中对拉力型锚杆抗拔试验进行了数值计算,并将计算结果与实测数据进行了对比,结果表明:
1)模型计算得到的荷载-位移曲线与实测数据接近,锚杆在验收试验最大荷载作用下未发生破坏。
2)锚杆在验收试验最大荷载作用下,锚杆轴力随着深度的增加而逐渐减小,不是均匀分布;超过一定深度后,锚杆轴力为0,即只有锚杆上部受力,超过一定深度的锚固段并不受力。
3)Abaqus中的粘结接触模型在拉力型锚杆抗拔试验数值模拟中具有适用性,有望推广到支护工程的安全评估的数值计算中。

