公平关切下双回收渠道闭环供应链决策和协调

王海燕，雷敬伟

（福州大学 经济与管理学院，福建 福州 350000）

1 引言

习总书记在十九大报告中指出：绿水青山就是金山银山。而回收再制造不仅实现了资源的循环利用，减少了环境污染，还可以给企业带来成本节约和竞争力的提升，有利于推动绿色经济的发展。

在众多的研究中，一部分学者将决策者的公平偏好引入了闭环供应链决策。闭环供应链中存在的公平关切问题是指闭环供应链中的成员不仅关心自己的利润，而且还会关注其他渠道成员的利润，如果产生不公平的感受，甚至会以自我利益牺牲的方式处罚对方。

张克勇等[1]首次将公平关切行为倾向引入到闭环供应链的定价决策中，构建了相应定价决策模型，并利用博弈理论对模型进行分析求解。Peng Ma[2]等基于一个制造商、一个零售商和一个第三方回收商组成的闭环供应链，研究了零售商具有公平关切情形下的四种回收渠道的最优决策。

而在闭环供应链研究中，有关公平偏好的研究多关注制造商或者零售商的公平偏好。即使有公平关切研究考虑到第三方，也多是视第三方受其他渠道成员公平偏好行为的影响，而没有考虑第三方的公平偏好行为影响其他渠道成员的决策。但是，在政府对回收市场的不断整顿下，各类小型回收商逐渐被大型回收商收购，像格林美这样的大型回收商，越来越专业化、正规化，规模也不断扩大。依靠对废旧品回收的专业处理技术，第三方在闭环供应链中扮演的角色越发重要。

本文研究零售商与第三方回收商同时回收的双回收渠道闭环供应链，分别从集中决策和分散决策两种情形来分析供应链各渠道成员的策略并进行比较分析，以探索当第三方具有公平关切行为时，（1）分散情形下，当第三方公平关切程度发生改变时，闭环供应链的最优决策以及相关利润、效用的变化；（2）分散情形下，回收废旧产品中可再制造的比例k的变化对闭环供应链的最优决策以及相关利润、效用的影响；（3）双回收渠道闭环供应链的协调机制设计。

2 模型描述及符号说明

2.1 模型描述

考虑单一制造商、单一零售商和一个第三方回收商组成的闭环供应链系统，制造商既可以通过加工新材料得到新产品，也可以通过对废品再制造得到再制造品，零售商负责将产品卖入到消费者市场，同时零售商与第三方回收商共同负责回收废旧产品，并且零售商与第三方回收商在回收废品时存在竞争，零售商和第三方回收商在回收到废品后将其出售给制造商，再由制造商进行再制造，构成闭环供应链，如图1所示。

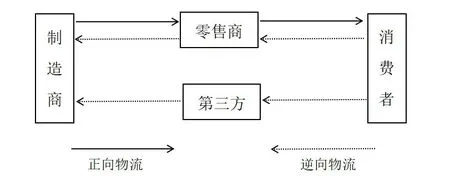
图1 零售商、第三方同时进行废品回收的闭环供应链结构

2.2 符号说明

cm为制造商使用新材料生产的单位成本；

cr为制造商使用回收到的废品生产的单位成本；

w为制造商的产品批发价；

p为零售商的产品零售价；

pm为制造商提供给零售商与第三方回收商的废品单位回收价格；

πm、πr、πc分别为制造商、零售商、第三方回收商的利润；

k为回收废弃产品中可用于再制造的比例。

2.3 模型假设

闭环供应链成员的决策受到多种因素的影响,为了聚焦研究重点，本文做出如下假设：

假设1 与公彦德等[3]，朱晓东[4]类似，设废品的回收量满足Gi=hpi-ξpj（i=1,2,j=3-i），其中G1为零售商废品回收量，G2为第三方回收商废品回收量；h（h＞0）为消费者对废品回收价的敏感系数，ξ（ξ＞0）为零售商与第三方间废旧产品的回收价格竞争系数；p1为零售商的废旧产品回收价，p2为第三方回收商的废旧品回收价。为了保证废品的回收 ，废 品 回 收 量G1+G2=(h-ξ)(p1+p2)＞0 ，由p1＞0,p2＞0可知h-ξ＞0。

假设2 产品的市场需求量为q=φ-βp，其中，φ表示市场容量，β（β＞0）表示消费者对零售价的敏感系数。为了保证产品的销售，市场需求需满足q=φ-βp＞0，即φ＞βp。

假设3 制造商使用回收的废品再制造的产品与使用新材料生产的产品在外观、性能等方面相同，并以同样的零售价在同一销售渠道进行销售。消费者对于采用不同材料生产的产品有着相同的接受度。

假设4 回收产品的质量水平存在差别，总回收量的k[5]（0≤k≤1）可以用来进行再制造，余下的1-k部分将进行拆解处理，单位获利为v。由于回收产品的质量水平不一，质量水平较高的回收产品被回收后可以通过再制造获利，而质量水平较低的回收产品被回收后可以通过拆解处理获利。通常情况下，回收产品通过再制造获利高于通过拆解处理获利，即满足Δ＞v。

假设5 设Δ=cm-cr表示使用废品进行再造节约下来的单位成本，为了保证制造商有回收再制造的积极性，需满足Δ＞0，即制造商使用回收废旧品进行产品生产具有成本优势。

假设6 参照张克勇[1]，引入公平关切系数λ。假设只有第三方回收商具有公平关切偏好，并以零售商的利润作为参照点来衡量自身的效用。用Uc表示第三方回收商的公平效用函数，设Uc=πc-λ(πr-πc)。 λ（λ≥0）为公平关切系数，λ=0时第三方回收商是公平中性的，λ越接近0表明第三方回收商的公平关切程度越弱，λ越大表明第三方回收商的公平关切程度越强，λ→∞表示第三方回收商极度关注公平，愿意为了保证公平而付出巨大的代价。πm、πr和πc分别代表闭环供应链中制造商、零售商以及第三方的利润函数，用π表示供应链系统的利润函数。

由以上所述可得制造商利润函数、零售商利润函数、第三方回收商利润函数、第三方回收商效用函数和供应链系统利润函数分别为：

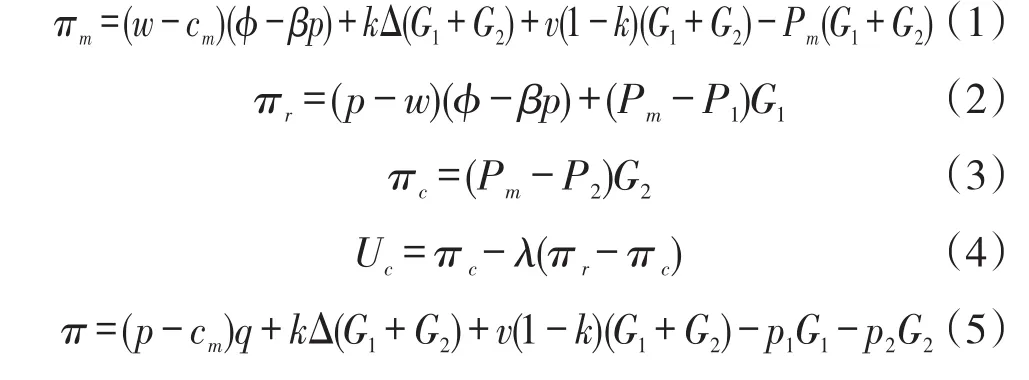
3 模型建立及分析

3.1 集中决策情形

在该情形下，制造商、零售商和第三方作为一个统一的整体进行完全合作博弈，各渠道成员以供应链系统利润最大化为目标，联合确定零售商回收价p1、第三方回收商回收价p2和零售价格 p。此时，供应链系统的利润函数为：

对π中决策变量 p1、p2、p分别求一阶偏导，并令其等于0，联立三个方程解得：

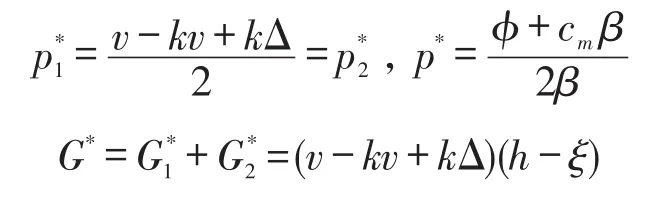
将p1、p2、p代入π可以得到集中决策下闭环供应链系统的最大利润为：

3.2 分散决策情形

在该情形下，制造商、零售商和第三方回收商均以独立决策者进行非合作Stackelberg博弈，并且闭环供应链由制造商主导，零售商和第三方回收商处于跟从地位。假设制造商不具有公平关切行为倾向，仅作为理性决策者以自身利润最大化为决策目标；第三方回收商为公平关切者，在闭环供应链系统中既关注自身所得收益的多少，同时也关注零售商所得收益，并且以自身的公平效用最大化为决策目标。

考虑第三方回收商公平关切时，Stackelberg博弈的决策顺序为：（1）制造商作为博弈的主导者首先确定批发价w和回购价 pm；（2）第三方与零售商作为博弈的跟随者同时决策：第三方根据制造商的回收价pm并且以零售商的利润πr为公平参考点确定从消费者回收废品的回收价p2；零售商根据制造商的回购价pm确定从消费者回收废品的回收价p1，根据制造商的批发价确定零售价p。利用逆向归纳法求解。对πr分别求 p和 p1的一阶导，对Uc求 p2的一阶导，并且令其等于0，联立解得：

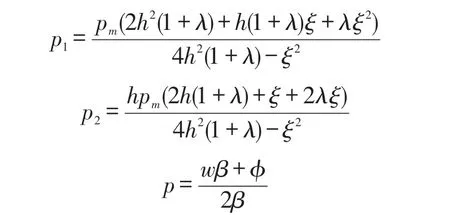
将 p1、p2、p代入式（1），对 πm求关于 pm、w 的海瑟矩阵：

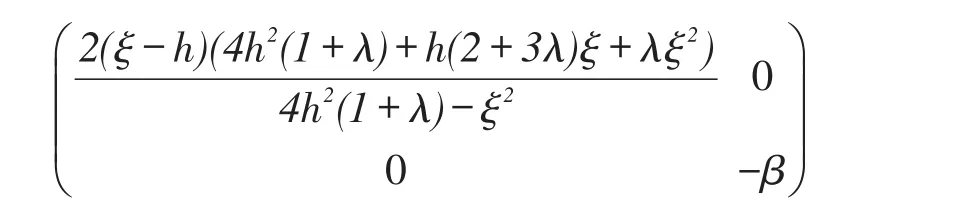
只有当4h2(1+λ)-ξ2＞0时，制造商的利润函数πm才是 pm和w的联合凹函数。把 p1、p2、p代入式（1），对 πm求 pm、w的一阶导，令其等于0，联立方程组解得：

将上述求得的各最优解带入各渠道成员的利润和相关效用函数，求得分散决策情形下的制造商利润、零售商利润、第三方回收商利润、第三方回收商效用以及供应链系统总利润分别为

3.3 模型的比较与分析

结论1 在集中决策情形下的零售价低于分散决策情形下的零售价，而零售商和第三方的回收价均高于分散决策情形下的回收价，供应链系统的总回收量高于分散决策情形下的总回收量。

证明：

结论2 在分散决策情形下，当第三方具有公平偏好时，渠道的最优批发价、最优零售价和制造商提供给零售商与第三方的最优废品单位回收价与公平关切系数无关。随着公平关切系数的上升，零售商的最优废旧品回收价格上升，第三方的最优回收价上升，零售商的废旧品回收量下降，第三方的废旧品回收量上升，系统总回收量增加，制造商的利润增加，零售商的利润减少，系统利润减小。

证明：

结论3 制造商的最优批发价和零售商的最优销售价与k无关。回收废旧产品中可再制造的比例k越高，回收价格越高，制造商支付回收方的转移价格越高，各回收方的回收量越大，闭环供应链中各渠道成员的利润越大。

证明：

3.4 数值分析

为了进一步分析分散决策下参数k、λ对第三方效用和闭环供应链总利润的影响，本小节利用matlab进行相关的数值仿真。首先对参数赋值：φ=200，β=2,c=40，Δ=15，v=2，h=20，ξ=10。并令k在（0，1）内变化，λ分别在（0，0.3）和（0，10）内变化，结果如图2、图3所示。

图2 分散决策下λ、k对第三方效用的影响

图3 分散决策下λ、k对供应链总利润的影响

由图2可以看出，随着第三方公平关切程度的增强，第三方的效用不断减少，甚至变为负值。这说明第三方的公平关切总是有损自身效用的，且公平关切程度越高，效用损失越多。而回收废旧产品中可再制造的比例k越大，第三方回收商的最优效用越高，并且k越大，最优效用增加越快。

由图3可以看出，随着第三方公平关切程度的增强，闭环供应链系统的总利润增加，但上升的幅度很小。这说明第三方回收商的公平关切行为对闭环供应链的总利润影响甚微。而随着回收废旧产品中可再制造的比例k的增大，闭环供应链的总利润会大幅度增加，并且k越大，闭环供应链总利润增加速率越大。

4 第三方回收商公平关切下的闭环供应链协调

二部定价契约是一种公共定价契约，将价格分为固定费和从量费。其中固定费与数量无关，而从量费根据具体的数量变化而变动。根据已有的研究，二部定价契约可以解决供应链中存在的双重边际效应问题，实现供应链协调，增加供应链的整体效益。

假设制造商分别与零售商和第三方协定Fr=(w,pm,Tr)和Fc=(pm,Tc)的二部定价契约，并记契约机制下各变量的上标为s，则模型问题如下：

制造商向零售商提供批发价格w，向零售商与第三方提供回收转移支付价格pm，同时向零售商收取固定费用Tr，向第三方收取固定费用Tc。模型博弈遵循Stackelberg博弈顺序，制造商占据主导地位，零售商和第三方同时为跟随者，三者之间进行两阶段博弈。

二部定价契约机制下供应链各渠道成员的利润和相关效用函数如下：

制造商的利润函数为：

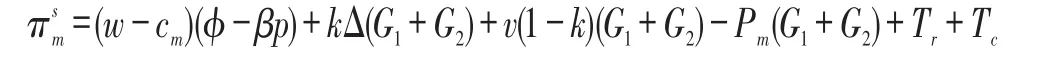
零售商的利润函数为：

第三方回收商的利润函数为：

第三方回收商的效用函数为：

分别对p1，p，p2进行一阶求导并令其等于0有

在Stackelberg博弈中，制造商作为领导者必须确保零售商的期望收益至少等于分散决策下的收益，第三方的期望效用至少等于分散决策下的效用，才能确保二部定价契约生效。于是有以下函数：

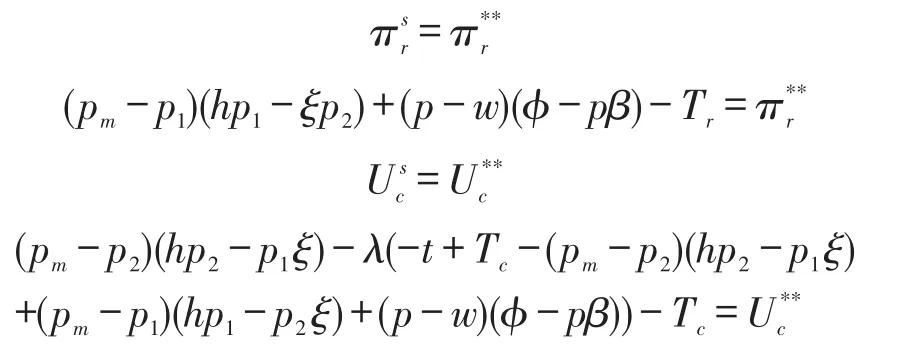
根据以上两个等式求出零售商和第三方交给制造商的固定费用Tr,Tc。

将上述相关参数带入制造商的利润函数中，并

将pm,w带入Tr,Tc，由于计算结果比较复杂，具体结果省略。

对以上求得的相关参数带入进行计算，可得到相关各方的决策变量：

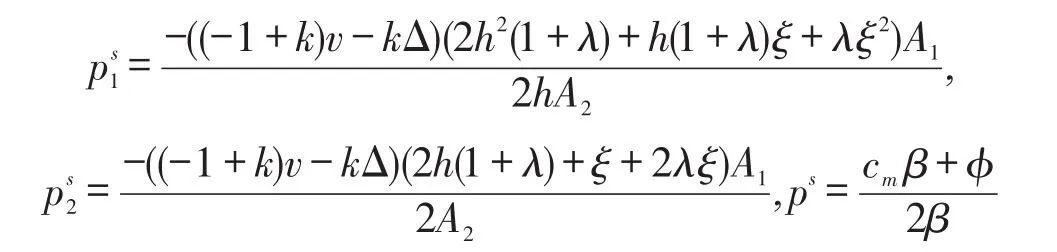
将求得的各参数带入进行计算，可求得渠道各成员的利润，第三方效用和闭环供应链总利润π，由于计算结果比较复杂，具体结果省略。

4.1 数值的比较与分析

结论4 实施二部定价契约机制后，与分散决策情形相比，零售商与第三方的废旧品回收价均上升，零售价降低。

证明：

结论5 实施二部定价契约机制后，与分散决策模式相比，制造商的批发价会降低，而制造商转移支付的回收价会提高。

证明：

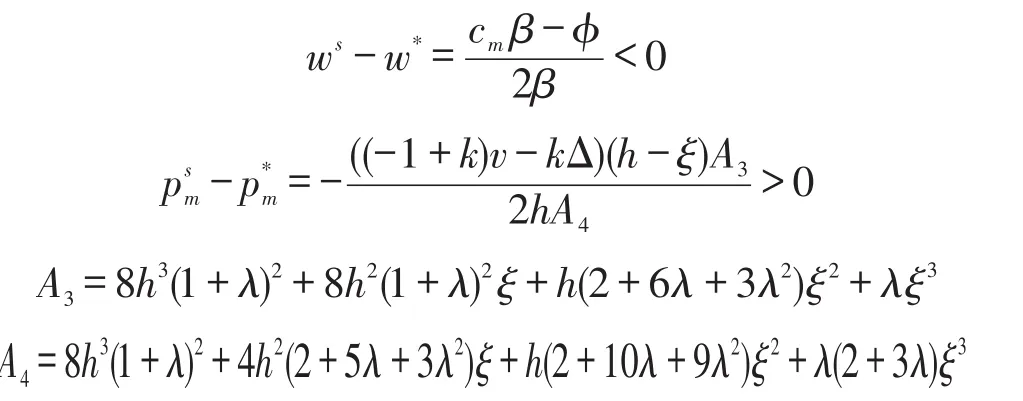
4.2 数值分析

为了更加简明的说明本文设计的二部定价契约可以有效协调双渠道闭环供应链，对各模型进行对比分析，本部分取λ=0.05，对相关参数赋值：φ=200，β=2，c=40，Δ=15，k=0.7，v=2，h=20，ξ=10 。得到不同决策情形下的最优结果，见表1。

表1 不同决策情形下的最优结果

从表1可以看出，二部定价契约下的零售价与集中决策一致，零售商和第三方的废旧品回收价以及闭环供应链总利润接近集中决策。相比于分散决策情形，二部定价契约的批发价更低，零售价、回收转移价格更高，零售商和第三方的废旧品回收价更高，供应链各渠道成员的利润不变或增加，系统利润更高。算例说明该二部定价契约可以有效协调闭环供应链，实现Pareto改进。算例结果与前文的理论模型分析结果一致，在一定程度上对前文的结论进行了论证。

5 结束语

本文以制造商主导的一个制造商、一个零售商与一个第三方回收商构成的双回收渠道闭环供应链为研究对象，考虑第三方回收商具有公平关切行为，研究了双回收渠道闭环供应链的最优决策和协调问题。研究发现：（1）与分散决策情形相比较，集中决策情形可以增进社会福利，给消费者提供更高的回收价格，提高废旧资源的利用率。（2）分散情形下第三方公平关切程度的增强会减少自身和第三方的利润，同时会减少自身的效用，但是对于制造商和供应链系统而言却是有利的。（3）分散情形下回收废旧产品中可再制造的比例k的增大能够明显增加第三方的效用，对于各渠道成员也均是有利的。（4）本文设计的一个两部定价契约可以有效协调双回收渠道闭环供应链，实现制造商、零售商和第三方的合作共赢。

本文的研究尚存在不足之处，如本文考虑的是信息完全对称情形，而有时公平偏好倾向是私有信息；其次，本文主要是针对单一零售商与单一第三方回收商回收进行研究，并未涉及多个零售商或多个第三方回收商情况；另外，本文只考虑了第三方具有公平偏好的决策及影响问题，没有考虑到零售商的公平偏好倾向。