材料初始缺陷对平纹编织C/SiC复合材料热残余应力的影响研究

白国栋，童小燕，姚磊江

(1.西北工业大学 航空学院， 西安 710072)(2.西北工业大学 无人机特种技术重点实验室， 西安 710072)

0 引 言

C/SiC复合材料作为高温热结构部件的重要候选材料已经在航空航天领域大量应用[1-2]。该材料由化学气相渗透工艺制备而成，在其加工和服役过程中，由于纤维和基体热膨胀系数不匹配导致内部产生的热残余应力是C/SiC复合材料在工程应用中需要考虑的重要因素[3]。热残余应力的存在不仅影响基体裂纹的产生和扩展，纤维的拔出和界面层剥落，而且影响材料的宏观力学性能。国内外对复合材料热残余应力问题做了大量的试验研究[4-7]和数值模拟[8-10]。目前，关于C/SiC复合材料热残余应力预测的研究较少。吕毅[11]通过SEM照片精确测量建立了C/SiC复合材料RVE有限元模型，采用间接耦合降温法，模拟计算了C/SiC复合材料轴向热残余应力；姚磊江等[12]通过稳态变温法和有限元分析，研究了C/SiC初始缺陷对其热膨胀系数影响关系。但这类研究并未考虑初始缺陷对热残余应力的影响，与实际情况有较大差异。

一般认为，各类初始缺陷的统计性存在是C/SiC复合材料性能产生分散性的根本原因，要较为精确地预测其材料性能就必须考虑初始缺陷分布特征的影响[13]。

本文在前述研究工作的基础上，以平纹编织C/SiC复合材料为研究对象，考虑各类初始缺陷的分布特征，基于稳态变温法研究平纹编织C/SiC复合材料的初始缺陷对基体面内方向热残余应力的影响关系，以期为材料研发和工程应用提供重要支撑。

1 C/SiC的初始缺陷

1.1 初始缺陷分类

平纹编织C/SiC采用化学气相渗透工艺法制备，主要组成部分为SiC基体，C纤维和界面层。这种制备工艺，在加工制造的过程中会产生大量初始缺陷。

C/SiC初始缺陷SEM图如图1所示，其内部的初始缺陷主要包括：环绕纤维束基体裂纹(A类)、纤维束交叉处孔洞(B类)、界面层剥落(C类)、环绕单丝纤维基体裂纹(D类)和单丝纤维间孔洞(E类)。其中A、C和D类初始缺陷为裂纹型缺陷，主要是因为基体和纤维的热膨胀系数不一致导致；B和E类初始缺陷为孔洞型缺陷，主要是因为SiC沉积过程不均匀导致。

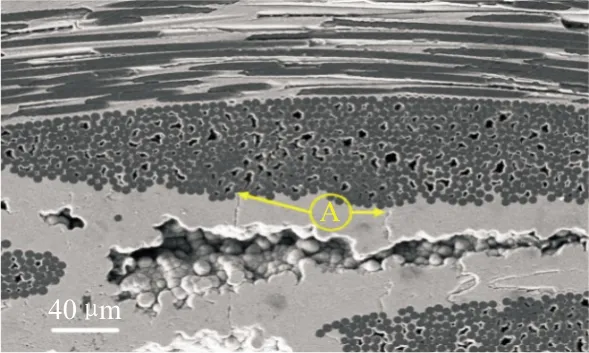
(a) A类缺陷

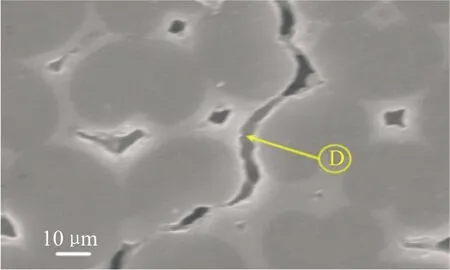
(d) D类缺陷

(e) E类缺陷

1.2 缺陷的分布特征

裂纹型初始缺陷在C/SiC复合材料中以各种裂纹形式存在，因此可以采用裂纹的长度L和单位体积的数量N两个参数表征裂纹的分布情况。其中，A类缺陷可以采用RVE宏观模型表征，C和D类缺陷可以采用RVE纤维束表征。但是，界面层通常不会完全脱粘，而是仅有一小段圆弧剥落，因此需要对其剥落的角度进行统计。任意选取五个界面层剥落角度样本值列出，结果如表1所示。

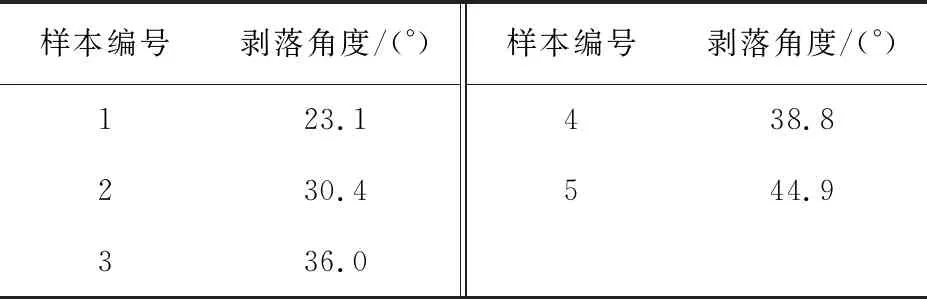
表1 界面层剥落角度样本值

孔洞型初始缺陷在C/SiC复合材料中以各种孔洞形式存在，可以采用孔洞的体积含量P和单位体积的数量N两个参数表征孔洞型缺陷的分布情况。其中，B类缺陷可以采用RVE宏观模型表征，E类缺陷可以采用RVE纤维束表征。对试样的B类和E类孔洞型初始缺陷进行统计，孔洞体积总含量P用百分数来表示，任意选取以上两类孔洞型缺陷的五个孔洞体积含量样本值，结果如表2所示。

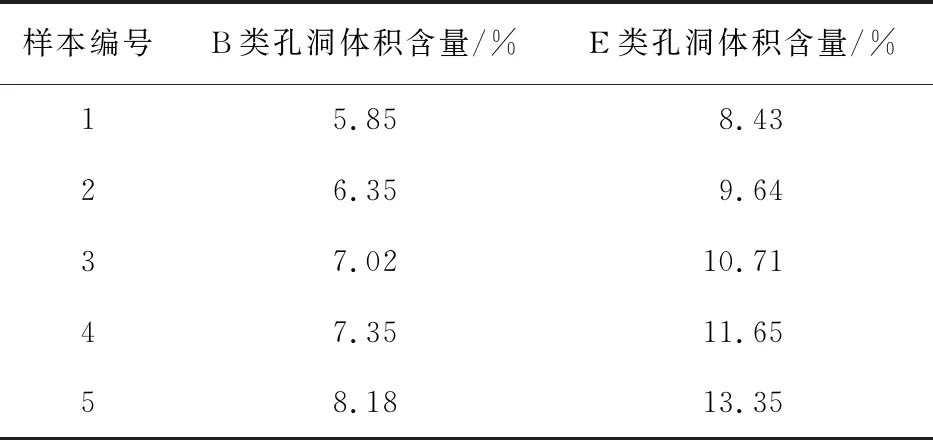
表2 单丝纤维间孔洞体积总含量样本值

2 宏观材料热残余应力的预测方法

2.1 含初始缺陷C/SiC的RVE模型

C/SiC复合材料的初始缺陷主要包括纤维束和宏观材料两个尺度，因此在建立模型时，需要分别建立RVE模型。要预测宏观材料的热残余应力，必须得到纤维束的力学性能参数和热膨胀系数。

宏观尺度的RVE模型根据材料的实际尺寸建立，C/SiC的铺层和约束条件如图2所示，建立C/SiC宏观RVE有限元模型如图3所示。模型由SiC基体和纤维束组成，依据统计结果，将A和B两类初始缺陷置入其中。根据孔洞体积含量的大小确定所需删除的单元数，采用删除网格单元法在纤维束交叉处置入孔洞。

图2 C/SiC铺层及约束条件

图3 宏观材料RVE有限元模型

依据纤维直径和界面层的厚度，建立纤维束RVE有限元模型如图4所示。参照A和B类初始缺陷的置入方法，根据统计结果，将C、D和E三类初始缺陷置入纤维束RVE模型。

图4 含初始缺陷的纤维束RVE有限元模型

2.2 稳态变温法预测热残余应力

利用FECM方法预测含缺陷的纤维束RVE的力学性能参数，预测含缺陷的纤维束RVE的热膨胀系数[14]。平纹编织C/SiC复合材料从制备温度(1 000 ℃)降到室温(20 ℃)再升到服役温度的整个过程不是瞬时完成的，可以看作一个稳态过程[15]。因此，通过施加当前状态的温度载荷(本文当前温度载荷均为室温)，模拟材料热残余应力的方法称为稳态变温法。假设模型某一顶点为坐标原点，对模型施加如下边界条件：

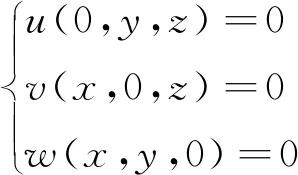
(1)

式中：u、v、w分别为x、y、x三个方向的平动位移。

利用图3所示的含初始缺陷宏观材料RVE有限元模型，按照如上所述的稳态变温法和边界条件，以MSC.PATRAN/NASTRAN为平台对平纹编织C/SiC复合材料任一主轴方向的热残余应力进行模拟，预测C/SiC复合材料基体面内方向热残余应力。在有限元模型中，假设1-2方向为宏观材料RVE有限元模型的面内方向，3方向为宏观材料RVE有限元模型的厚度方向，计算得到宏观材料RVE基体面内方向的热残余应力为154.45 MPa，梅辉等[16]利用无残余热应力原点法测得平纹编织C/SiC复合材料SiC基体室温(20 ℃)时的面内热残余应力为134.85 MPa，说明预测效果较好。

3 初始缺陷对热残余应力的影响

按照上述过程分别计算不含缺陷和含单一缺陷时宏观材料基体面内方向热残余应力。A和D类缺陷的分布稳定，因此只需各计算一次。B、C和E类缺陷存在统计分布特征，因此按照统计样本值需要各计算五次。计算得到不含缺陷和分别只含A和D类缺陷时宏观材料基体面内方向的热残余应力如表3所示。

表3 宏观材料基体面内方向的热残余应力

平纹编织C/SiC复合材料从制备温度(1 000 ℃)降到室温(20 ℃)，材料整体产生收缩现象，纤维束轴向热膨胀系数小于SiC相的热膨胀系数，在降温过程中其变形小于SiC相的变形，SiC相受到纤维束轴向的拉应力，因此，预测出的值均为正值。从表3可以看出：与不含缺陷时相比，A类缺陷使宏观材料基体面内方向的热残余应力升高，D类缺陷使宏观材料基体面内方向热残余应力降低。

将计算得到的B、C和E类缺陷样本值对应的宏观材料基体面内方向的热残余应力绘制成曲线图。

B类缺陷对宏观材料基体面内方向热残余应力的影响如图5所示。

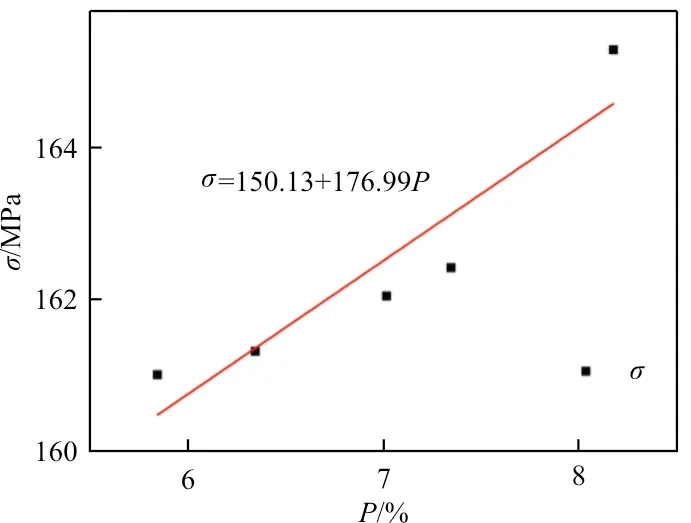
图5 B类缺陷对宏观材料基体面内热残余应力的影响

从图5可以看出：随着B类缺陷的增大，宏观材料基体面内方向热残余应力增大较快。

C类缺陷对宏观材料基体面内方向热残余应力的影响如图6所示，可以看出：随着C类缺陷的增大，宏观材料基体面内方向热残余应力急剧减小。

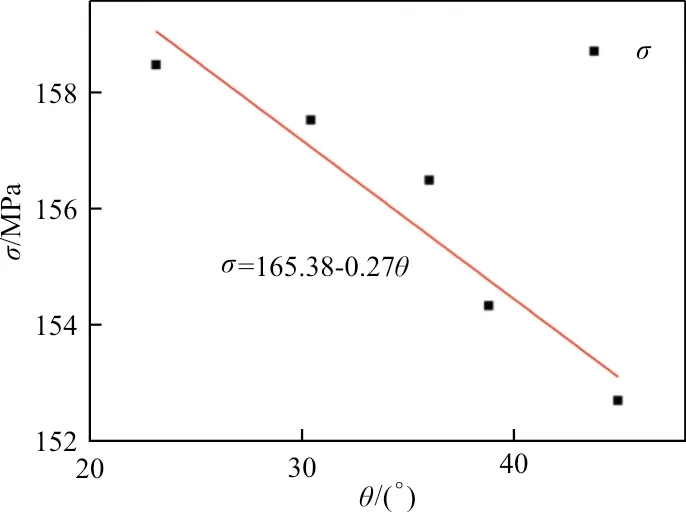
图6 C类缺陷对宏观材料基体面内热残余应力的影响

E类缺陷对宏观材料基体面内热残余应力的影响如图7所示，可以看出：随着E类缺陷的增大，宏观材料基体面内方向热残余应力出现小幅增大。

图7 E类缺陷对宏观材料基体面内热残余应力的影响

从平均意义上讲，五类初始缺陷对宏观材料基体面内方向热残余应力的影响从大到小依次为D、A、E、C、B。将各图中的曲线进行线性拟合可得到各类初始缺陷与宏观材料基体面内热残余应力之间的定量映射关系，即图5～图7中给出的表达式。

4 结 论

(1) 基于稳态变温法预测了平纹编织C/SiC复合材料基体面内方向的热残余应力。预测值与试验值对比效果较好，证明了预测方法的正确性和可靠性。

(2) 与不含缺陷模型相比，各类初始缺陷的存在均对宏观材料基体面内方向热残余应力有较大影响。从平均意义上讲，五类初始缺陷对宏观材料基体面内热残余应力的影响从大到小依次为：环绕单丝纤维基体裂纹、环绕纤维束基体裂纹、单丝纤维间孔洞、界面层剥落、纤维束交叉处孔洞。

(3) 通过稳态变温法，得到了各类初始缺陷与宏观材料基体面内热残余应力之间的映射关系，为材料研发与工程应用提供参考。