运动地板减震垫的冲击实验及结构参数优化1)

花军 张昊 王宏棣 刘一楠 刘宇宸

(东北林业大学，哈尔滨，150040) (黑龙江省木材科学研究所木材综合利用重点实验室) (东北林业大学)

运动地板是一种能承受运动员高强度运动且提供运动保护的特殊地板，体育场馆铺设的运动地板与普通地板的主要区别在于其具有良好的结构性能[1]。运动地板结构组成中，减震垫位于地板龙骨与混凝土地面之间，具有不同结构参数的减震垫在运动地板抵抗冲击载荷能力上存在较大差别。其冲击吸收性能的高低直接影响运动员在运动时身体承受冲击力的大小，而冲击力的大小与运动地板减震垫参数有密切的关系。因此，探究及优化运动地板减震垫结构参数和提升运动地板冲击吸收性能具有重要的科学意义及应用价值。

1 运动地板冲击实验

1.1 实验器材

地板与检测仪器：冲击实验以单层龙骨运动地板作为研究对象，其由面层地板、毛地板层、防潮层、龙骨层、减震垫等组成，结构如图1所示[2]。

单层龙骨运动地板及测试仪器具体参数如表1所示。

表1 检测仪器与地板参数

减震垫：冲击实验采用市场上最常见的5种减震垫作为实验材料，参数如表2所示。

1.2 测试原理

A95型冲击测试仪主要由落锤、冲击头、螺旋形弹簧、底座、冲击力传感器等组成，测试原理如图2所示[3]。冲击测试仪产生冲击力部件为重锤，以6 340 N标准冲击力冲击运动地板；所产生的冲击力除部分被运动地板吸收外，剩余的冲击力以反冲击力Fw的形式被冲击力传感器检测收集并传送给信号处理仪；信号处理仪已预先标定混凝土地面反弹力 值，信号处理仪将反弹力Fw与混凝土地面上的反弹力Fc两者数值通过公式(1)计算，得出冲击吸收率Fr[4]。按照GB/T 20239—2015《体育馆用木质地板》标准中关于运动地板冲击吸收性能要求，采用冲击吸收率Fr数值的大小表达运动地板冲击吸收性能的优良。

(1)

式中：Fr为冲击吸收率(%)；Fw为运动地板上反冲击力算数平均值(N)；Fc为坚实地面(水泥地面)反冲击力算数平均值(N)。

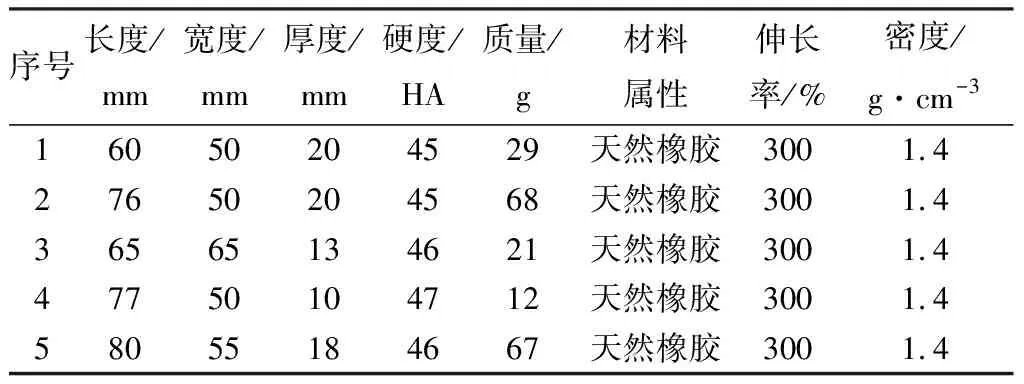
表2 减震垫参数

注：天然橡胶具有良好的弹性拉伸性能及较好的耐屈挠性，其拉伸强度为17～25 MPa、弹性模量为2～4 MPa、耐屈挠10万次出现裂口；体育地板室内使用温度为20～25 ℃，低于天然橡胶最高使用温度70 ℃；橡胶材料在1～4 a内均可保持良好的冲击吸收性能。

1.3 方案设计

1.3.1 方法

按照GB/T 20239—2015中关于运动地板检测点布置原则与要求，检测点的布置原则：以运动地板或实验室试件的结构几何中心作为起始检测点，按照对称原则逐步向周围展开布置检测点，检测点布置如图3所示。

冲击实验采用某专用地板有限公司生产的单层龙骨运动地板作为实验试件，结合实验所用地板拼装尺寸(3 600 mm×3 600 mm)，选取图4所示5个点作为检测点。

运动地板背面减震垫布置如图5所示，单块拼装运动地板试件共设有7条龙骨，间距400 mm，每条龙骨安装3个减震垫，一种减震垫完成冲击实验后更换另一种进行冲击实验[5]。

实验测试现场充分模拟体育地板的实际使用环境，考虑环境温湿度对人及体育地板影响因素，并依据人体运动舒适温湿度范围及体育地板安装及使用温湿度标准要求，将测试现场环境温度设定为20～25 ℃；环境湿度设定为40%～50%。进行冲击实验时，运动地板上每个检测点进行5次冲击试验，分别记录每次冲击实验后运动地板的反冲击力与冲击吸收率并求取平均值，冲击实验测试现场如图6所示。

1.3.2 减震垫影响参数确定

根据实际单层龙骨运动地板安装减震垫的结构参数要求，影响单层龙骨运动地板减震垫冲击性能参数包含：长度(L)、宽度(W)、厚度(T)、面积占比(A)、体积占比(V)、硬度(H)、质量(M)等。为确定合理的减震垫结构参数，选取5种不同结构参数减震垫进行冲击试验，得到此条件下运动地板的反冲击力Fw，减震垫结构参数及反冲击力实验结果如表3所示。

表3减震垫结构参数及反冲击力实验结果

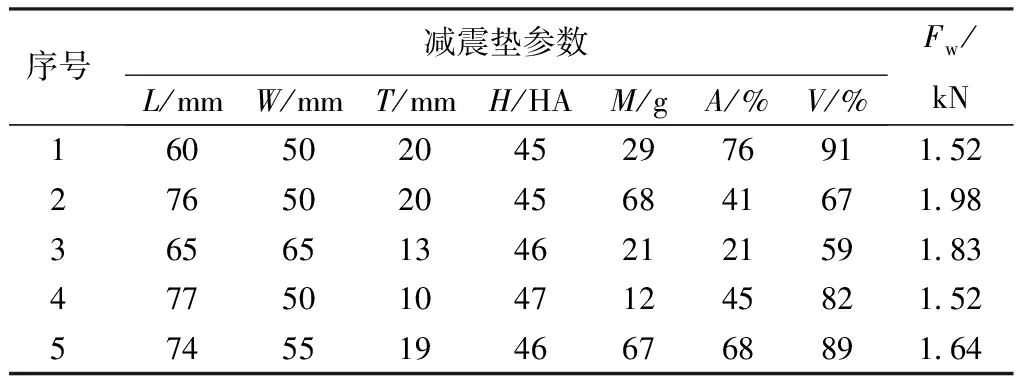
序号减震垫参数L/mmW/mmT/mmH/HAM/gA/%V/%Fw/kN1605020452976911.522765020456841671.983656513462121591.834775010471245821.525745519466768891.64

单层龙骨运动地板减震垫的结构参数及反冲击力实验结果数据采用SPSS多元线性回归方程拟合算法[6]进行分析计算，得到7个模型参数(减震垫结构参数)对应的标准化系数值，如表4所示。

表4 参数标准化系数表

表4中各模型参数对应标准化系数的绝对值越大，则说明该参数的权重系数越大，即对反冲击力的影响越大，绝对值3～5为最优，L、W、T、A、V标准化系数的绝对值均大于3。为此，选定L、W、T、A、V5个参数作为影响减震垫反冲击力的结构参数。

1.3.3 冲击实验结果

减震垫影响参数为5个，依据试验要求和目标选择5因素4水平，自由度为15，实验次数为16的L16(45)正交试验表。构建的正交试验水平因素表，如表5所示。

由正交试验因素水平表，可设计得到实验次数为16的L16(45)正交试验设计方案，并通过单层龙骨运动地板冲击实验[7]得到运动地板在安装有不同结构参数减震垫时的反冲击力试验结果，如表6所示。

表5 正交试验因素水平

表6 正交试验设计及结果

表6中试验参数(影响因素)已通过SPSS多元线性回归方程拟合算法确定出影响参数的主次顺序且做出筛选，为避免赘述不再对试验结果进行参数影响显著性分析。

表6的建立与实验结果(反冲击力)的获取，可以初步得出在多种减震垫结构参数通过正交试验作用下，运动地板减震垫反冲击力数值变化明显，说明减震垫结构参数选取较为合理，为接下来模型算法建立与对比分析奠定了基础。

2 模型算法建立与对比

2.1 BP神经网络预测模型算法

2.1.1 模型算法结构的确定

Hornik et al.[8]已证明：若输入层和输出层采用线性转换函数，隐含层采用Sigmiod转换函数，则含一个隐含层的多层感知器神经网络能够以任意精度逼近任何有理函数。BP神经元网络模型算法的设计中，一般靠增加隐含层神经元数量来提升计算精度，其训练效果比增加隐含层更容易实现。因此，根据模型算法输入变量与输出变量之间关系，确定预测模型算法隐含层神经元设计数量为6个。BP神经网络预测模型算法创建函数为newff，隐含层数为3个，隐含层转换函数为Sigmiod，输出层的转换函数为purelim。输入层神经元的数量由需要优化的对象数量决定，模型建立神经元数量为5个，分别为L、W、T、A、V。输出层神经元的数量由输出的目标决定，本次实验的输出变量为Fw，输出层为1[9]。构建的BP神经网络预测模型如图7所示。

2.1.2 模型算法训练

BP神经网络预测模型算法训练过程即采用实验训练数据(算法程序将实验数据分成训练数据及测试数据两种)对模型算法进行数据运算训练处理，目的使模型算法对于线性或非线性函数输出具有预测能力。基于实验条件，神经元网络预测模型训练数据采用实验室方式获取，可以较好地满足神经网络预测模型的训练要求，且训练好的预测模型预测精度较高。

神经元网络预测模型参数设置：迭代次数为5 000次，学习率0.001，均方根误差1×10-5；选用train作为训练函数；调用函数[pn,minp,maxp,tn, mint,maxt]=prestd(p,t)对输入数据以及输出数据进行数据进行归一化以及反归一化处理，加快训练模型算法收敛性，提高预测精度[10-11]。

应用MATLAB软件，将实验数据用于已建立好的BP神经网络预测模型算法进行训练。程序训练迭代次数达到5 000次时，预测数据与真实值(测试数据)对比结果如图8所示。预测精度决定性系数R2=0.860 77>0.5，说明模型算法能够较好地反映输入与输出参数之间的函数关系，已经到达训练精度要求。预测误差如图9所示，训练好的模型算法得出的预测数据与测试数据(真实值)误差值在0～0.07，均小于0.1，说明所建立的预测模型具有较高的预测精度[12]。

2.2 SPSS多元线性回归方程拟合算法

2.2.1 SPSS多元线性回归拟合过程

为探究非线性弹性材料减震垫的结构参数与反冲击力之间线性关系，应用SPSS多元线性回归方程拟合算法，该算法是一种揭示有多个输入变量与输出变量之间的线性关系的算法。应用SPSS软件将冲击实验数据导入，选择分析→回归→线性，进入分析页面对话框，选择L、W、T、A、V为自变量，Fw为因变量，方法中选择“步进”，完成以上设置后，点击“确定”。

2.2.2 SPSS多元线性回归拟合结果

SPSS软件数据处理结束，可得到表7—表8参数值。

表7 模型参数

表7中，调整值R2为0.811，说明拟合参数模型能够反映真实数据的81.1%，具有良好的参考性；Durbin-Waston(德宾—瓦特逊)检测值为1.907，接近2，说明自变量(减震垫结构参数)之间相关性较低；ANOVA方差显著性参数为0小于0.05，说明模型方差分析显著性较好[13-14]。

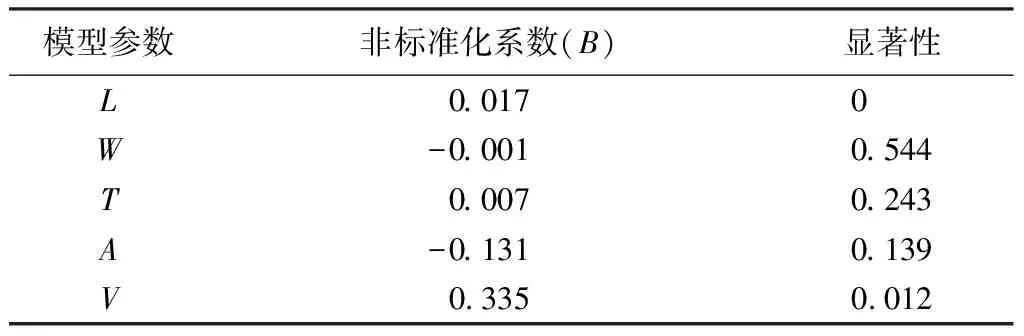
表8 非标准化系数及显著性

表8中显著性值越接近0，说明参数对方程显著性越好，其中L与V显著性值较小即具有良好的显著性。可以通过获取对应的非标准化系数值，得到反冲击力的函数表达式：

Fw=0.017L+0.335V。

(2)

式中：Fw为运动地板上反冲击力算数平均值(N)；L为减震垫长度(mm)；V为减震垫体积占比(%)。

2.3 算法对比分析

为对比BP神经网络预测模型算法与SPSS多元线性回归方程拟合算法的精确性，选取结构参数如表9所示的3组减震垫，并进行对比性的冲击试验，得到反冲击力数值。

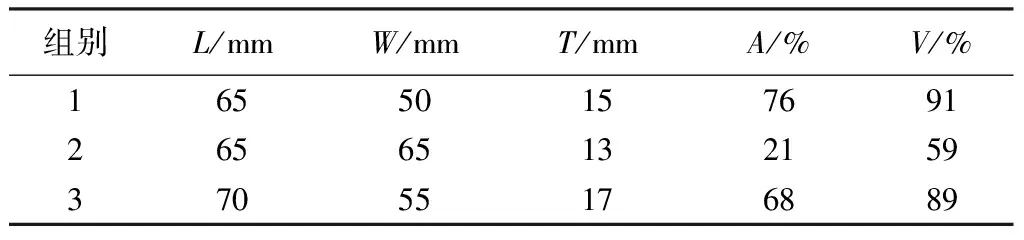
表9 检测用减震垫结构参数

分别采用BP神经网络预测模型算法与SPSS多元线性回归方程拟合算法，对表8中的减震垫参数计算出两者反冲击力数值。二者数值与实验值对比计算得到表10所示的两种算法反冲击力的对比误差率。可以看出，SPSS多元线性回归方程拟合算法与实验对比误差率比BP神经网络预测模型算法与实验对比误差率平均高13.4%，说明BP神经网络预测模型算法的预测值更接近实验值；BP神经网络预测模型算法对于减震垫的结构参数与反冲击力之间关系描述更准确可靠，该算法能够较好地反应减震垫结构参数与反弹力之间的关系。

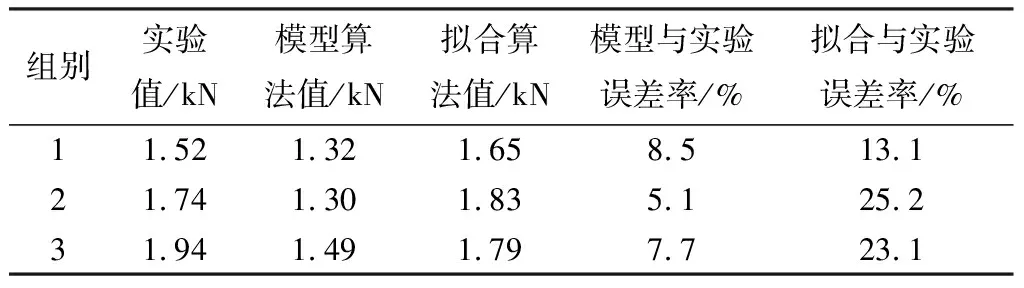
表10 模型算法与拟合算法反冲击力的对比误差率

3 减震垫结构参数优化

BP神经网络预测模型算法能够较好地反应减震垫结构参数与反冲击力之间的关系。根据减震垫结构参数在实际安装中的变动范围，利用训练好的模型算法对给定范围内的减震垫结构参数进行反冲击力预测，得到48组预测数据。

对于优化目标选取，考虑到减震垫的材料利用率以及成本问题，减震垫结构参数中体积占比为有效体积与理论体积的比值，理论数值越小则材料利用率越高。反冲击力作为最主要反映运动地板冲击吸收性能的指标，数值越小说明运动地板冲击吸收效果越好。为提高实验数据结果的简练性，优化目标将反冲击力及体积占比的代数和最小值作为优化目标。对已获得48组预测数据进行整理，得到图10所示各组反冲击力与体积占比代数和趋势图。

图10表明反冲击力与体积占比代数和最小值即为趋势线的最低点，最低点数值为1.92，对应预测组别为第17组。查询表11(48组数据较多，只列出部分)中第17组预测减震垫结构参数数值。该预测数据为最优减震垫结构参数，具体参数L、W、T、A、V为55 mm、55 mm、12 mm、30%、40%。在此参数下定制出减震垫样件，进行冲击实验，其实验反冲击力结果为1.61 kN，相比于预测结果1.52 kN误差为6%，符合预测模型与实验误差范围要求。应用公式(1)计算安装有样件减震垫在反弹力为1.61 kN下的冲击吸收率为74%。

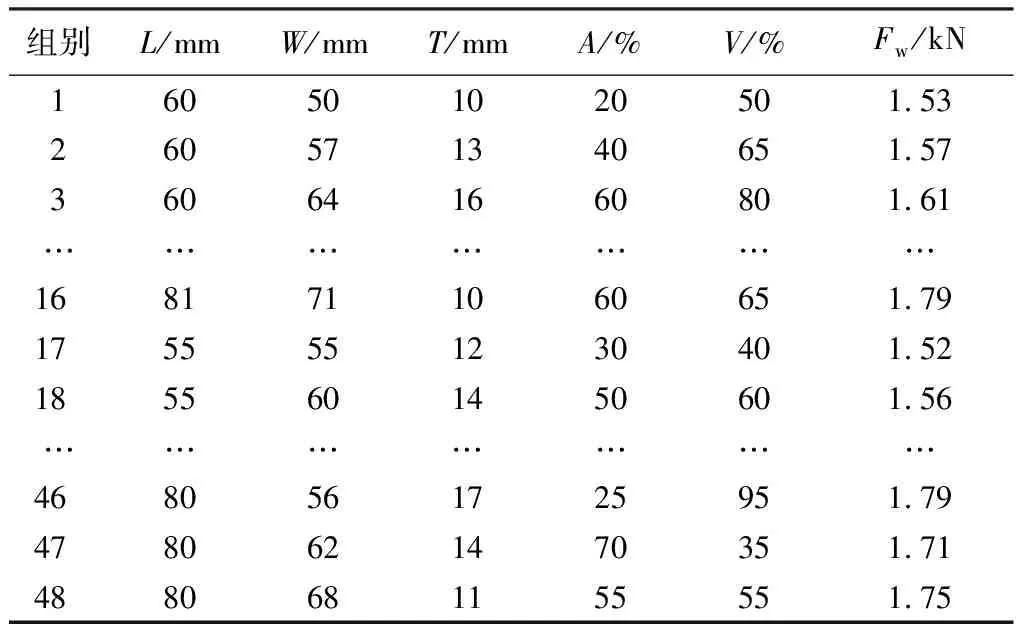
表11 BP神经网络模型预测数据(部分)

按照GB/T 20239—2015《体育馆用木质地板》，关于运动地板功能性指标中冲击吸收率需满足≥53%要求，以及未进行优化的减震垫冲击吸收率一般在55%～70%。这说明在安装具有该参数减震垫下的运动地板具有良好冲击吸收性能，能良好的满足运动地板实际使用要求。

4 结论

基于冲击实验数据，采用BP神经网络预测模型算法构建了减震垫结构参数与反冲击力之间的预测模型；采用SPSS多元线性回归方程拟合算法得到减震垫结构参数与反弹力之间的函数方程为Fw=0.017L+0.335V。

经冲击实验数据与两种算法所得结果对比，得出BP神经网络预测模型算法数值与实验数值较为接近且相对误差率较小，即所建立的BP神经网络预测模型算法具有较高精度。

对获得的预测数据以体积占比与反冲击力代数和最小作为优化目标，得到减震垫最优结构参数L、W、T、A、V为55 mm、55 mm、12 mm、30%、40%；对该结构参数减震垫进行冲击实验，实验结果表明此参数下的运动地板冲击吸收率为74%，满足标准及实际使用要求。