基于Q矩阵特征提取的建模及可视化分析
颜远海,杨莉云
(广东财经大学华商学院,511300,广州)
0 引言
在大数据的背景下,越来越多的平台数据被整合,科学的决策也越来越数字化、智能化。其中对大量数据的特征提取可以很好地认知事物的特征与本质,从而形成规律、经验和知识。数据的可视化主体数据之间关联性的特征通过科学布局把精美的图表展示给决策者,但可视化程度以及可视化的内容一直是数据可视化设计师需要认真考量的内容。而可视化程度离不开对多维数据的降维处理,离不开良好的特征提取算法。特征提取的准确性依赖于特征库的存在,特别在多属性数据的情况下,研究属性或属性组合与特征库之间的关系,一直是研究者们探讨的话题。本文利用Q矩阵理论[1]对认知诊断的影响,提出Q矩阵下的特征提取算法,并深入探索属性之间的关联性[2],科学地分析可视化程度和内容。本文的方法可以应用到主体(比方说公司、客户、人际关系等)间关联性研究并为之提供科学的依据。
1 问题导向
本文研究的问题主要有:Q矩阵如何去识别属性之间的关系,并建立属性关系模型,这种模型是否有行业推广性?Q矩阵如何建立属性与特征之间的关联,是否可以减少对特征库的依赖性,因此对于可视化程度和可视化内容需要进行挖掘分析。为了说明完整的问题链,特用图1描述问题的逻辑关系[3]。
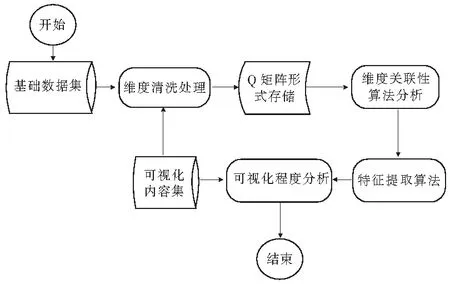
图1 总体业务流程图
在采集到合适大小的数据集后,首先解决的是根据不同的可视化目的,清洗不同属性(属性内容及深度)的数据,利用Q矩阵将清洗后的数据进行数据属性化处理工作,通过算法得出属性之间的关联性,并且在没有特征库存在的前提下,寻找新特征算法[3-4]。最后才是对可视化内容和可视化程度做出科学分析。
本文重点解决3个问题,第1就是属性清洗后Q矩阵存储的方式,以及建立针对可视化目的的Q矩阵模型[1-2];第2就是特征提取算法,为了提高特征提取的准确性,在特征提取之前就已经做了属性关联分析,通过属性关联分析对多维数据进行适当的降维处理;第3就是可视化程度分析,为了说明不同可视化内容与可视化程度之间的关系,可建立内容集与可视化程度之间的模型集。
2 Q矩阵形式存储
特征提取过程中需要使用到属性(属性)与项目(对象)之间的关联矩阵(Q矩阵),Q矩阵的行表示项目,列表示属性。为了节省存储容量和计算速度,把具备相同属性的项目进行合并处理,设计一种简化后的Q矩阵(QS矩阵)[1,6],但是不管如何进行简化,在大数据量的面前,如果项目有N个属性,那么简化后的记录都有(2N-1)个,当然这里讨论的是定性二值属性。为了更好地说明项目的重要性,特在存储列中增加一项count值,用来计数基础数据集中类别项目数。
假设某可视化的内容需要N个属性值,在基础数据集中有M个项目(对象),其中M远大于(2N-1)个,则构成的的Q矩阵为M*N矩阵型。而经过修改后的Q矩阵为((2N-1)·(N+1))矩阵型。
属性关联模型具备封装性且全部属性值为1的必要条件是该前置属性为1。显然在图4中当A=1时,B或C才可能=1;反之,当B=1时,A=1。
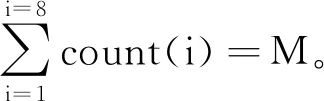
2.1 属性规则空间建模
项目属性之间有一定的关联性,当某属性A明显是属性B的前置条件时,则属性B的发生的必要条件是属性A的发生。比如规定学生“成绩=优秀”的前置条件必须是“分数>=90”。则在Q矩阵中可以适当进行简化。为了把这些明显规则找出来,特参考文献[1,7]中关于简化Q矩阵的算法方式,通过例2简要说明算法结果。
在以上例1中,假设属性1是属性2的前置条件,则(0,1,-,-)是不可能发生的项目,则总体项目数为6<8。当N值较大时,简化Q矩阵(QS矩阵)较大程度减少项目数。对于这种不可能发生的项目的CountE值(CountE为异常项目计数值)相对较小但不等于0的情况,采用直接清理的方式进行处理。而如果CountE值占比较大的情况下,采用以下公式进行平滑处理,目的是使得其影响最小。
(1)
其中:CountR(i)为平滑处理前正常的项目计数值,sum(CountR)为正常项目计数值总和,sum(CountE)为异常项目计数值总和。CountR′(i)为平滑处理后正常项目计数值。“「」”向下取整。
定义1:孤立属性:指的是没有任何前置与后置条件的属性。相反如果有前置或后置条件的属性则为非孤立属性[7-8]。
对于孤立属性进行正常Q矩阵存储,而对于非孤立属性在Q矩阵中的存储方式前提需要建立规则空间模型,因此一个数据集可能包含多个属性空间模型和1个孤立属性矩阵[6,9]。
|D|代表D中的数据行数。
R*S={Rt∪Ss|Rt∈R,Ss∈S}
其中, ΔS为网格单元的面积, ΔΩ为网格单元对球心的立体角, θ为纬度角, 在0到π/2之间; φ为经度角, 在0到2π之间. Δθ为纬度角方向的间距, Δφ为经度角方向的间距, 都为定常值.
(2)
其中R、S为矩阵,Rt,Ss为矩阵行。
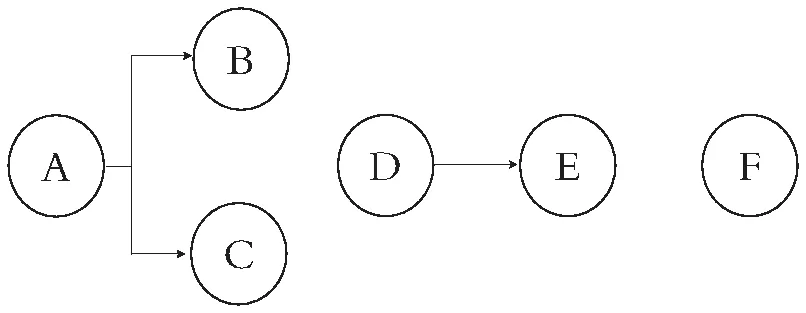
图2 属性关系样图
经过式(2)对图3中的矩阵进行连接后形成了30×7形式QS矩阵(每一项增加count计数值列),经过属性规则空间建模后,例3中的计算量和存储量比建模前减少了一半多(数据项由原来的448减少到现在的210。存储单元由原来的64减少至30)。
黄花三宝木TrigonostemonlutescensY. T. Chang et J. Y. Liang是大戟科(Euphorbiaceae)三宝木属Trigonostemon Bl. 植物,其主产于广西南部,生长于石灰岩山地的灌木林中,为广西特有药用植物[1]。在我国和泰国,三宝木属植物是应用广泛的民间药[2],此属植物大多具有防腐、杀菌、止泻、化痰的功效[3]。现代研究结果表明,三宝木属植物所含化学成分以萜类[4]、生物碱类[5]及菲类[6]等化合物为主,具有抗肿瘤[4]、抗病毒[5]、抑菌[7]、杀虫[8]等药理活性,是一类值得深入研究与开发的药用植物资源。
90年代初期,受邓小平南巡的影响,香港大约8万多家制造工厂北移到了内地,企业开张的鞭炮声连绵不断。也催生了一批帮忙夹带货物的水客,王卫也是其中一员。而王卫和其他人不同的是,他在其中看到了商机,在碌碌的生活中找到了出路。
将变量G.Nodes.Weight添加到Q矩阵,添加图的属性权重。Weight变量必须是M×1 数值向量,其中M= numedges(Q)。
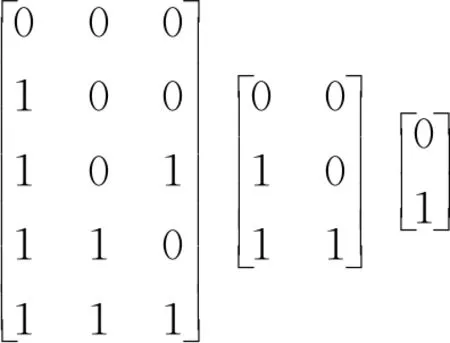
图3 属性关系QS矩阵
连续性属性值可以借助信息熵[10](式(3))进行离散化处理。
Weight[7]=[10,7.99,7.70,4.00,4.34,3.81,4.65]-1。
(3)
(4)
数据集D及类别集合C={c1,c2, …,ck}。
count(Ci):类别Ci在D中出现的次数。
p(Ci):Ci在D中出现的相对频率。
p(Ci)=count(Ci)/|D|,
比如某项目有6个属性(分别属性A~F),当进行首次简化处理后得到((26)×7)形式矩阵(即需要存储448个数据项,需要64个数据单元)。如果A是B、C的前置条件,D是E的前置条件,F为孤立属性,则分别2个属性规则空间模型(如图2)和1个孤立属性矩阵。分别对它们建立Q矩阵后(图3)进行矩阵存储后采用参考文献[7]的方式获得QS矩阵。
2.2 QS矩阵的改进策略
在属性规则空间模型中,可能存在间接前置条件下的模型。
定义3:间接前置:当属性A是属性B的直接前置,而属性B又是属性C的直接前置,则属性A是属性C的间接前置。反之属性C是属性A的间接后置。
定义4:结构封装性:属性空间关联模型结构只具备一个的前置属性,则该模型具备结构封装性。很明显,封装性可以具备层次性,例如以下属性模型。
图4中,F={{B,D}{C,E,F}}具备封装性,因为它们具备A这个前置属性,F1={B,D}也具备封装性。以下将所有具备封装性的集合统称F集合。称A为唯一前置属性,称{B,D}为第1子集,{C,E,F}为第2子集(这里也是最后1子集)。
雨水集蓄利用工程建设要求集、蓄、输、灌系统相互衔接配套,结构安全实用,降雨径流集蓄效率高。具体建设标准如下:
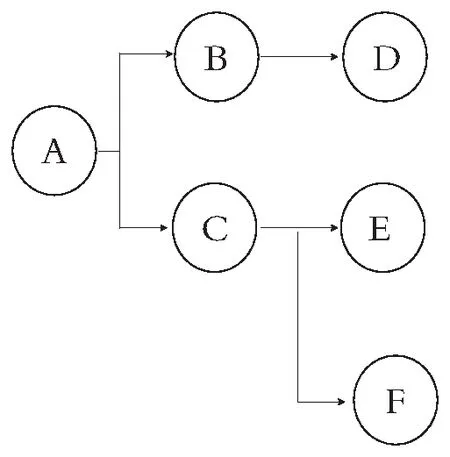
图4 某属性空间模型
为了建立Q矩阵,先对F集合中的子集进行Q矩阵存储,再逐步进行扩张,直到将F集合中的属性全部进行Q矩阵存储。每一次增加只增加F子集中的前置属性。算法(QS-F算法)如下。

1: 输入:F集合,唯一前置属性X2: 输出:QS矩阵T3: S=F的第1子集Q矩阵4: R=S;5: T=空矩阵;6: While S!=F的最后1子集7: {{Do8: S进行Q矩阵存储9: T=T×S 10: S=S∪{S的前置属性}11: While X⊄S}12: R=F的下1个子集Q矩阵13: S=R;}14: 输出 T
在定义边与结点权重的基础上,定义路径权重,此实验总计6条路径,分别如下。
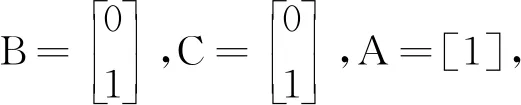
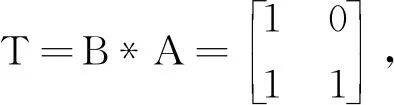
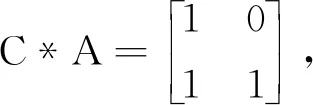
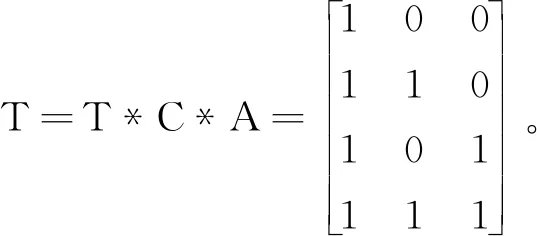
从以上算法中可以看出,当T中的项目数只包括A=1的情况,而A为唯一前置条件,只有A发生的时候,其它属性才可能发生,删除了[0,0,0]的情况。这种状态反映属性间无关联性,进一步反映出属性间边及路径权重值为0,将这种情况不写入QS矩阵中。实验表明,QS-F算法适合大多数具备树型结构的属性规则空间模型。
3 实验设置与条件
3.1 创建实验属性层级矩阵图
属性个数n=7,属性之间的关联为层级关联性,如图5,关联生成矩阵如图6[11]。 为了充分说明实验模型中算法的可行性及有效性。特模拟出特定的属性树型层级模型,研究的重点主要就是可视化属性权重及属性间关联权重,过程中涉及基于QS存储优化。因此实验设置过程中需要对实验数据的质量要求比较高。
影响公立医院建立科学合理完善的内部监督评价机制的因素有很多,其影响最大的因素是:运营过程中各部门权责不明,工作标准不明确;医院内部缺乏专业性的评价团队,虽然有外部专业的评价团队可以聘用,但是长时间不利于医院的发展,增加医院的运营成本;内部控制评价机制缺乏激励措施,这大大降低了工作效率,不利于完善监督评价机制。
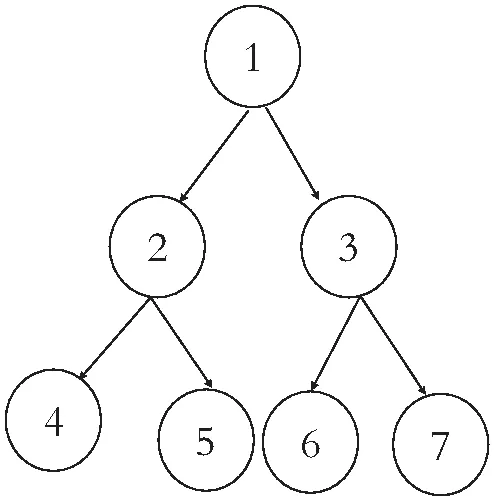
图5 属性层级模型

图6 Q矩阵

图7 部分属性QS矩阵
图6表示每个结点与另一个结点的直接后继结点之间的关系,图7表示属性QS矩阵总共25×7矩阵,每一行代表一种状态,总共25种可能性状态,具体可见表1属性状态表。
朱晓仑从不放松对自己的要求,做到对党忠诚、个人干净、敢于担当、不怕困难。柳南区食品药品监管工作量是一直因地域广、人口结构复杂而位列柳州市四城区之首,监管对象占柳州市1/3以上,监管压力非常之大。朱晓仑一手抓创建,一手抓监管,全力推进食品药品监管各项工作。他带领全局同志建立了城区三级监管体系,探索创新的服务模式,使基层食品药品体制改革取得突破进展,食品药品安全监管职能承接有序,监管工作稳中有升。2015年,成功承办广西示范性药品突发事件应急演练,得到国家总局和自治区局高度好评。
3.2 项目计数值countR'(i)
根据公式1定义的项目计数值可得不同项目的计数值如图8所示。
3.3 定义属性权重
3.2.1 全身性并发症 肾功能衰竭是保肢失败常见的致死原因。长时间休克状态肾缺血以及清创不彻底致毒素吸收均可导致急性肾功能衰竭。肾功能衰竭一旦发生,应尽早截肢,保全生命。本组1例老年女性患者因藏獒咬伤致小腿长段毁损离断,因既往有高血压病史,再植术后2 d出现大面积脑梗死、昏迷不醒,家属放弃治疗,出院后死亡。患者年龄大、有高血压病史、患肢损伤重、失血多,是否再植应慎重考虑。
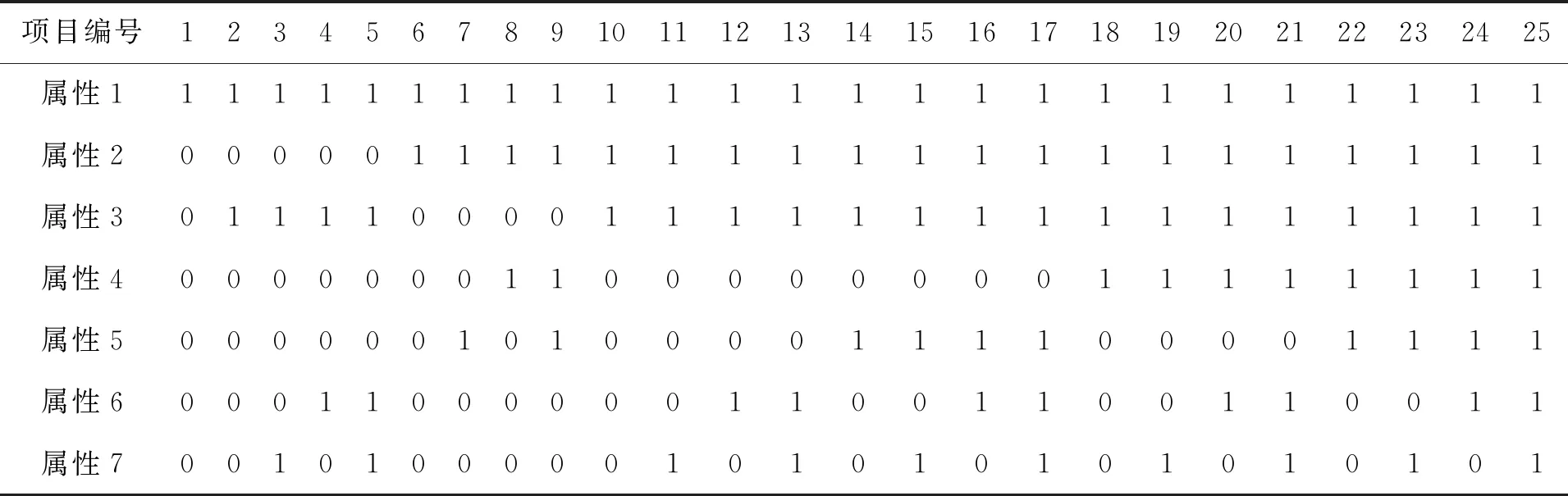
表1 项目属性状态表
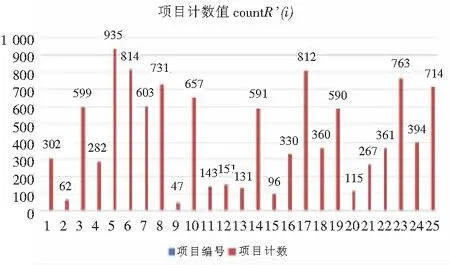
图8 不同项目的计数值
本实验根据结点层级来定义属性权重值,结点越高权重越高,反之越低。本文也根据了QS矩阵列来定义属性权值,代表每个结点属性出现的频繁度[10]乘以10作为属性权修正值。频繁度值为该结点在所有项目中出现的总次数占总体项目数的比值。
定义2:数据集D按照属性A的分裂条件分裂出的m个子数据集分别为D1,D2,…,Dm,则entropy(D,A)(式(4))综合这m个子数据集的信息熵就可以作为衡量一个属性A优劣的度。
3.4 定义边权重
新增变量G.Edges.weight[6],定义图的边权重,边权重参数值定义如下。
自磨机排矿经直线筛筛分后,3 mm以上的矿石返回自磨机再磨,3 mm以下的矿石泵送到Φ3.2×5.4 m球磨机排矿泵池,输送到一段Φ350 mm×8旋流器组进行分级,沉砂进入球磨再磨,溢流进入一段弱磁机选别,弱磁尾矿经圆筒筛隔粗后给入一段强磁,强磁选尾矿直接抛尾,弱磁和强磁混合粗精矿进入Φ2.7×3.6 m球磨机排矿泵池,输送到二段Φ350 mm×8旋流器组分级,沉砂进入球磨再磨,溢流进入二段弱磁机、强磁、摇床选别,改造后工艺流程见图2。
李咏说他自己是“宅男”,可以一个月不出家门,这个一点儿不假。他的人生志向特简单,就是“老婆孩子热炕头”。所以他除了工作,但凡还有点儿时间和精力,就全用在了家庭建设上。
G.Edges.P[i]=1/2×Weight[i,2],其中Weight[i,2]与第i条边有关联的2个结点的权重值之和。所以G.Edges.P[i]=[8.99, 8.85, 5.85, 6.16, 5.75, 6.17]-1,i=1,2,3,4,5,6。
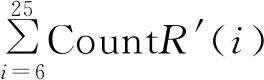
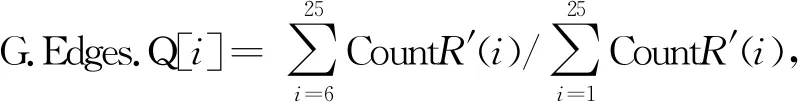
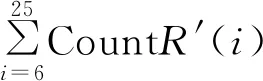
在拍摄《秋菊打官司》时,电影里有个雪景,追求极致的张艺谋,坚持要用自然雪景,也就是说,在零下二三十度的气温下,巩俐要在雪里完成一切动作。巩俐尊重导演的安排,结果戏拍完了,她也直接在雪地里晕倒了。在《西游记之孙悟空三打白骨精》中,为了更好地诠释角色,她提前看了许多国内外关于妖精、吸血鬼的书,还自创了“无呼吸表演”。“观众看不到白骨精的呼吸,因为妖精不需要这些。”
G.Edges.Q[i]=[0.80, 0.77, 0.40, 0.43, 0.38, 0.47]。
定义边权重值G.Edges.weight[i]=G.Edges.P[i]×G.Edges.Q[i],实验计算得出:
G.Edges.Weight[i]=[7.19, 6.81, 2.34, 2.65, 2.18, 2.90],i=1,2,3,4,5,6。
3.5 定义路径权重
根据以上算法,特列举出图2生成QS矩阵主要的生成过程。其中A为唯一前置属性,取值为1。
G.Path[i]=[‘1-2’,‘1-3’,‘1-2-4’,‘1-2-5’,‘1-3-6’,‘1-3-7’]。G.Path是字符型,代表路径,对G.Path增加Weight方法,计算G.Path.Weight的方法如下。
G.Path.Weight[i]=VEG(PWeight[i])×VEG(QWeight[i]),
其中:VEG(PWeight[i])为与第i条路径相关联结点权重的平均值,VEG(QWeight[i])为与第i条路径相关联边的权重平均值。此实验中数据如下
VEG(PWeight[i])=[8.99,8.55,7.33,7.44,7.17,7.45];
VEG(QWeight[i])=[7.19,6.81,4.77,4.92,4.50,4.85];
G.Path.Weight[i]=[64.64,58.23,34.96,36.60,32.27,36.13]。
这也让我们思考,在短视频领域,流量如何成为正能量?一段时间,也有一些“三俗”的东西借“土味”之名传播,夸张妆容、雷人雷语,甚至打暴力色情擦边球,似乎带上“土味”就可以理所当然地不雅,这不仅违背了公序良俗,逾越了法律边界,也不可能有持续的生命力。
4 实验结果与分析
4.1 属性权重分析
属性权重代表着属性的重要程度,通过比较很容易得出属性1权重值最大,越外围的值代表重要程度越大,在分析关键因素时,可通过属性权重来定义关键因素的重要程度。当考虑到重要因素时,重点也要考查关系网中所处的作用是什么,是全局性作用还是局部性作用。本文实验中属性1是具备全局性作用,也就是说当属性1的发生与否会影响全局的。而属性2与属性3的发生在特定的子范围内会发生影响。
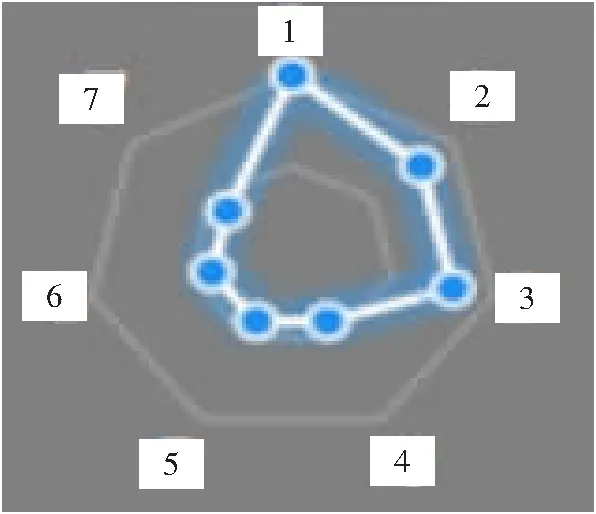
图9 结点权重图
4.2 边权重分析
边权重代表属性之间关联权重,是一个属性与属性之间重要程度的衡量指标,本实验当中通过科学的计算方式将属性权重通过可视化方式表示,雷达图显示,越外围的权重越大,代表关联也就越大,关系也就越紧密(图10)。
为了保证建筑设计质量、降低建筑安全隐患、确保国家及人民的生命财产安全,1997年建设部在上海、武汉、苏州、合肥等城市进行施工图审查试点工作[2],并于2000年开始实行了施工图审查制度。但传统的审图方式效率低且漏审、错审的概率高。2014年住建部《关于推进建筑业发展和改革的若干意见》建市〔2014〕92 号文件要求:“改进审批方式,推进电子化审查,加大公开公示力度,推进建筑市场监管信息化与诚信体系建设,推进BIM等信息技术在工程设计、施工和运行维护全过程的应用,提高综合效益,探索开展白图替代蓝图、数字化审图等工作” [3]。

图10 边权重图
4.3 路径权重分析
路径权重表示结点到另一个结点之间路径的权重,是一个属性与另一个属性关联程度的重要衡量指标。本实验中,属性路径越短,权重值越大,路径越长,权重值越小。从图11中可以看出,一个路径的长度相同,权重值相当取决于属性权重值以及边权重值。
4.4 属性关联权重意义分析
在对象特征提取中,需要通过一定的方法选择一个属性子集,很多情况下初始可以随机选取,
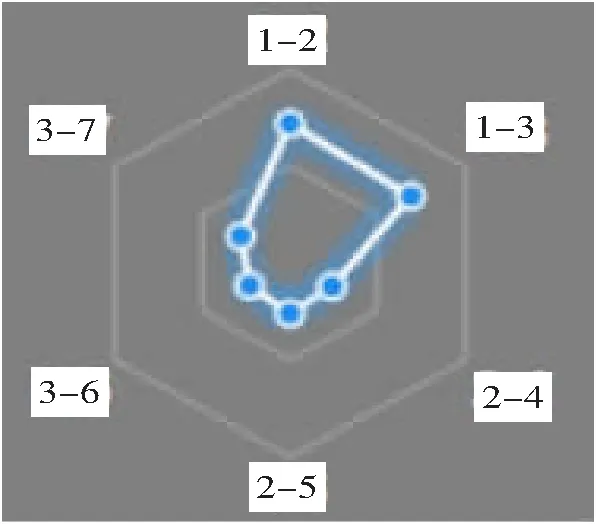
图11 路径权重
这种方式虽然可行,但是也要付出相当大的代价,在认识属性之前,可以进行属性层级认识,建立Q矩阵,识别有价值的记录,去除噪声数据,从而更好地进行特征提取。本文考虑到属性权重,关联边权重,以及关联路径权重,通过3个方面的分析,可以更好地知道某数据集的特征。
同样,研究属性之间关联性算法,也能够在实际应用场景有指导意义,比方说,在社会关系学中,可以衡量一个公司与公司之间业务关联的权重,对认识一个公司或其它对象有相当大的指导意义。
5 结束语
本文从Q矩阵理论进行属性关联分析,属性之间的关联具备层次性,而属性关联模型可能有线型、网状型、树型、离散型等模式,因此在识别属性间的关联通常根据经验不断地进行修正,然后通过Q矩阵进行存储,为了更好地识别属性之间关联而达到对象特征提取的目的,需要对不符合属性层级模式的数据进行清洗,为了了解属性权重,需要读到数据集中有关该属性的全部数据值,属性的权重意义代表着对特征贡献程度,也代表着对其它属性的影响程度。
冠心病组胆红素、HDL浓度低于非冠心病组,血尿酸水平、TC、LDL高于非冠心病组;均有统计学意义(P<0.05)。两组比较上TG无统计学意义(P>0.05)。表明高TBIL、IBIL、DBIL、HDL为冠心病的保护因素,UA、LDL、TC为冠心病危险因素;见表2。
本文从结合Q矩阵理论,对数据进行去除噪声数据处理,并对合理数据进行数据统计与分析,建立属性权重、属性关联权重、属性间路径权重,通过算法计算。实验证明,属性权重值属性间关联权重值计算方式,权重越大,对特征提取的贡献值也越大,数据集特征同样也取决于属性间路径权重,如果某路径值越大,代表着该路径趋势越明显,出现的概率越大;反之,概率越小。本文研究应用可用于对主体(比方说公司、客户、人际关系等)间关联性分析,并为之提供科学的依据,但是所考虑的因素有限,比方说属性值只考虑了二值划分,定义权重因素过于依赖数据样本等。基于本实验研究,还有很多工作需要深入研究,比方说考虑更多因素来定义权重问题,考虑多值属性的关联研究等。

