管廊基坑开挖对既有长江隧道变形的影响
杨卫星, 官天培, 刘长庚, 卢方伟, 王丹生
(1. 武汉市政工程设计研究院有限责任公司, 湖北 武汉 430023; 2. 南京南瑞继保电气有限公司, 江苏 南京 211102; 3. 华中科技大学 土木工程与力学学院, 湖北 武汉 430074)
随着我国基础设施建设的快速发展以及城市地下空间的二次开发利用,城市内的深基坑工程越来越多。这些基坑在施工过程中,极有可能与既有地下隧道发生交叉或穿越。例如天津地铁1号线上方的某深基坑工程[1],南京上跨地铁1号线的某基坑支护工程[2],广州地铁1号线上方物业建筑群基坑施工[3]等。
针对深基坑开挖对下方既有隧道变形的影响,国内外学者已经进行了相关研究,并取得了一些有价值的成果。在理论研究方面,Kerr[4]提出了一种全新的三参数地基梁模型,并结合工程实例监测和仿真数据,验证了该理论模型的有效性和优越性;吉茂杰和刘国彬[5]提出了开挖宽度影响系数以及残余应力系数的概念,并依据残余应力理论,推导出基坑开挖卸载后下方既有隧道变形估算的实用性计算公式;张治国等[6]采用Winkler弹性地基梁理论,结合两阶段分析方法计算了隧道的位移及内力,理论解与仿真结果和现场实测数据吻合较好。在数值研究方面,高广运等[7]以上海某地铁隧道侧边基坑工程为背景,采用数值仿真的方法对整个施工过程进行了模拟,发现采用坑外二次加固技术可以有效阻断位移的传递,从而控制相邻隧道的变形;戚科骏等[8]着重开展了不同基坑开挖方式对邻近隧道影响的相关研究,发现基坑底部加固深度、施工对称性以及开挖过程中的时间因素,都对邻近隧道最终变形有影响,并建议在施工方式选择时应慎重考虑。
纵观国内外学者对该类问题研究的报道,多为讨论基坑与既有隧道垂直或平行的情况,鲜有报道长条形深基坑与既有大型过江隧道斜交的研究案例。本文以武汉和平大道三角路处长江隧道上方与其斜交的综合管廊深基坑开挖工程实例为背景,利用大型有限元软件ANSYS建立三维有限元模型,研究了基坑开挖卸载后,既有长江隧道的竖向变形规律,并依据Winkler弹性地基梁理论对数值模型进行了验证,最后较系统地研究了加固土的长度、宽度、密度以及弹性模量等因素对隧道竖向位移的影响,提出了控制隧道竖向位移的有效措施,为正在进行的武九管廊深基坑开挖工程提供技术指导。
1 基于弹性地基梁理论的隧道竖向变形计算方法
采用Winkler弹性地基梁理论计算基坑开挖后下方既有隧道竖向位移时,通常分为两步进行。第一步先计算由开挖卸载引起的隧道轴线处的附加应力;第二步再将该附加应力转化为线荷载,建立关于隧道竖向位移的微分方程;最后利用边界条件,求解该方程,得到隧道竖向位移的解析解。
设基坑开挖后,基坑底部作用有大小为q的均布荷载,基坑深度为d,荷载作用范围以及荷载与隧道的空间相对位置如图1所示,平面投影相对位置如图2所示。
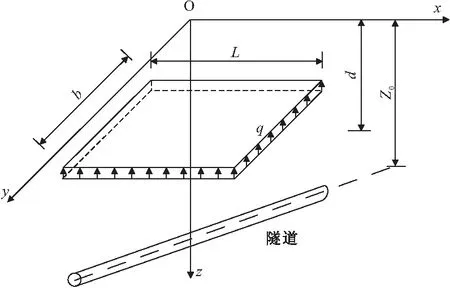
图1 计算模型简图

图2 计算模型平面投影
对于埋深为z0、纵轴线平行于均布荷载且与荷载轴线成β角的隧道,根据张治国等[6]的研究成果,可求得基坑开挖引起的隧道轴线处的竖向附加应力σz,在此不赘述。
得到隧道轴线处附加应力σz后,利用Winkler弹性地基梁理论计算隧道竖向位移,其计算模型如图3所示。
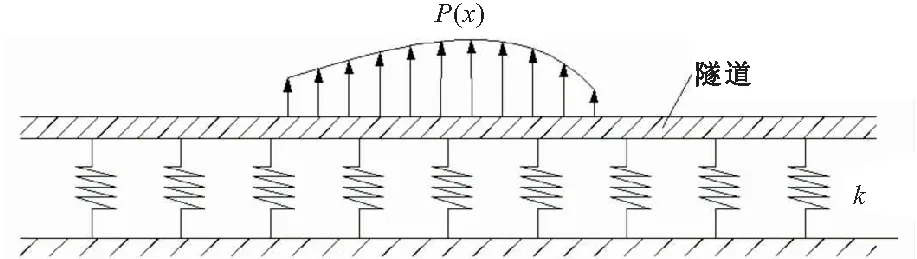
图3 Winkler弹性地基梁简化计算模型
将地基土对隧道的约束简化为刚度系数为k的弹簧,建立关于隧道竖向位移S(x)的四阶微分方程如下:
(1)
式中:EI为隧道等效纵向抗弯刚度;p(x)表示隧道所受附加线荷载,按p(x)=σzD计算,D为隧道外径。
求解该微分方程时,应先将其化为齐次方程,得到齐次方程的通解,之后将其在隧道附加线荷载范围内积分,得到非齐次方程的特解。由此可得隧道竖向位移表达式为[9]:
(cos(λ|x-η|)+sin(λ|x-η|))dη
(2)
式中:η为积分变量;K,λ可按下式计算:
(3)
(4)
式中:H为隧道底部至下方坚硬土层顶部的距离;Eeq为H范围内的土层弹性模量的加权平均值。
2 工程案例
2.1 基坑工程总体概况
为结合北环铁路的搬迁,推动武昌临江片整体开发,需在原武九铁路下方新建武九线综合管廊工程。该综合管廊基坑开挖时,在和平大道三角路处,会跨越既有武汉长江隧道,与其呈45°斜向交叉。管廊基坑与既有长江隧道现场平面相对位置关系如图4所示。

图4 管廊基坑与隧道平面
该节点处基坑开挖宽度约为13.7 m,设计开挖深度为9.3 m,支护结构采用型钢水泥土搅拌墙+2道内支撑,基坑底与长江隧道管片顶部净距为9.2 m,管片外径11.6 m,厚度0.5 m,采用C50预制钢筋砼结构;按设计要求,基坑底向下采用三轴搅拌桩满堂加固,加固深度为8 m且与基坑同宽。

基坑开挖前,先进行型钢水泥土搅拌墙、坑底土体加固以及冠梁施工;待基坑开挖至第一道砼支撑底部0.5 m时,现浇施工第一道砼支撑并养护到设计强度的80%,再继续向下开挖至第二道钢支撑底部0.5 m处,进行钢腰梁以及钢支撑的布置,最后继续开挖至基坑底即可。基坑支护结构布置以及与长江隧道的立面相对位置关系,详见图5。
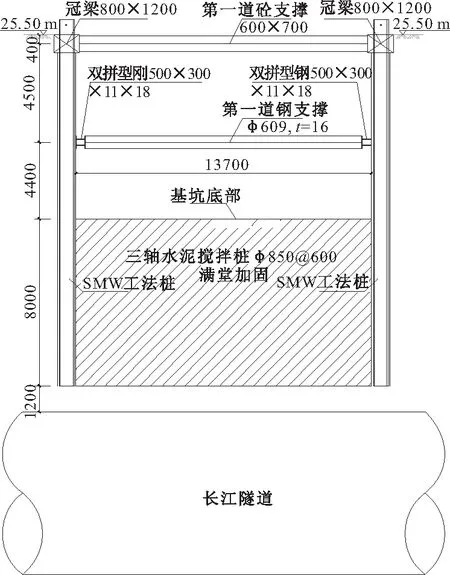
图5 基坑支护结构布置/mm
2.2 工程地质条件
场地地基土层分布如下:杂填土,标高范围25.500~23.900 m,厚度1.6 m;淤泥质粉质黏土夹粉土,标高范围23.900~7.700 m,厚度16.2 m;粉质黏土夹粉土,标高范围7.700~5.000 m,厚度2.7 m;粉砂夹粉土,标高范围5.000~2.600 m,厚度2.4 m;粉砂,标高范围2.600~-14.500 m,厚度17.1 m。地基中各土层物理力学指标如表1所示。
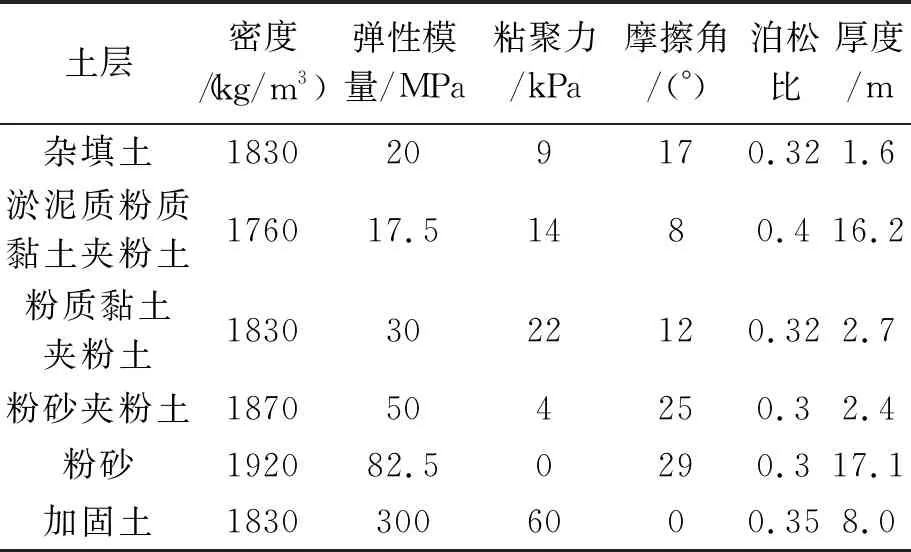
表1 各土层物理力学指标
3 三维有限元建模及模型验证
3.1 模型建立及参数选取
本文基于ANSYS有限元分析软件,对长江隧道上方的管廊基坑开挖进行三维有限元数值模拟。基坑开挖宽度为13.7 m,同时为了避免边界条件对计算结果的影响,模型宽度可取基坑开挖宽度的3~5倍[10],则该模型宽度可取为60 m。结合长江隧道的埋深以及与基坑的相对位置,整个有限元模型尺寸可取为112 m×60 m×40 m。
建模分析时,支护结构以及长江隧道衬砌采用线弹性本构模型,土体采用Drucker-Prager弹塑性本构模型;冠梁、腰梁以及两道内支撑采用Beam188单元模拟,地基土以及长江隧道管片采用Solid45单元模拟。由于型钢水泥土搅拌墙中,水泥土仅作为止水帷幕而H型钢是主要的受力构件。按抗弯刚度等效原理,将型钢水泥土搅拌墙等效为0.3 m厚的钢板墙[11],采用Shell181单元模拟。
模型四周采用水平位移约束,底面采用竖向位移约束,顶面为自由面。管廊基坑开挖对长江隧道影响的有限元模型如图6所示。

图6 有限元模型
在网格划分时,为了提高网格质量以及网格划分效率,本文在封底加固土底部与长江隧道顶部之间设置一层0.5 m厚的过渡层,采用Solid92实体单元模拟;场地土以及加固土的计算参数采用表1中的数据,支护结构以及隧道管片的计算参数如表2所示。

表2 支护结构相关参数表
3.2 荷载步设置
管廊基坑施工顺序及荷载步设置如下:
(1)通过单元的生死功能,将支护结构处单元杀死再加载重力,求解得到初应力文件,然后将其作用在模型上,进行初始地应力场平衡;
(2)施工型钢水泥土搅拌墙、冠梁,进行基坑底部土体加固处理;
(3)开挖地表至第一道砼支撑底以下0.5 m范围内的土体,并施工第一道支撑;
(4)开挖由砼支撑底以下0.5 m至钢支撑底以下0.5 m范围内的土体,并施工第二道支撑及腰梁;
(5)开挖由钢支撑底以下0.5 m至基坑底部范围内的土体。
3.3 模型验证
由于获取既有长江隧道顶部竖向位移的监测数据较为困难,为了验证数值模型的正确性,本文依据Winkler弹性地基梁理论,结合本工程实际参数,采用Matlab计算软件编写程序,计算出管廊基坑开挖后,既有长江隧道管片顶部竖向位移的理论解,并与数值解作对比;由于模型的对称性,仅计算长江隧道西线的相关结果,如图7所示。

图7 长江隧道西线顶部竖向位移数值及理论解
由图7可知,基于ANSYS有限元分析软件的数值解和Winkler理论解竖向位移曲线最大值分别为8.13,7.21 mm;Winkler理论解对应的竖向位移曲线较本文数值解曲线更为平缓,即在30~55 m范围内,数值解比理论解略大,而在其它位置,数值解比理论解略小。数值解与理论解的隧道竖向位移曲线吻合较好,数值解峰值略大于理论解,整体偏于安全,验证了数值模型的有效性。此外,本文隧道管片顶部竖向位移数值计算曲线形状与周泽林的计算及测试结果[12]类似,亦可验证本文所用数值计算方法的正确性。
需要指出的是,本文得到的数值解中考虑了土体的塑性;而Winkler弹性地基梁理论解中将土体对隧道结构的约束简化为土弹簧,认为土体为理想的弹性材料。由于考虑塑性的土体材料对隧道结构的约束较弱,理想弹性的土体材料对隧道结构的约束较强,导致数值解峰值略大于Winkler解,但计算得到的长江隧道西线顶部竖向位移数值与理论曲线整体吻合较好。
4 隧道上浮位移及影响因素分析
既有隧道上方出现开挖卸载时,隧道管片结构会出现上浮,为了保证隧道运营安全,其上浮位移不得超过20 mm的限值[13];为了防止隧道管片环向拼接缝张开量过大,导致隧道结构产生漏水病害,隧道管片纵向变形的曲率半径不得小于15000 m[13]。
4.1 隧道管片上浮位移分析
图8为按设计要求加固封底厚度取8 m时,管廊基坑开挖完成后长江隧道东、西线管片顶部竖向变形曲线;由图可知,开挖完成后隧道顶部竖向变形呈现中间大、两边小的变化规律,东西线顶部最大上浮值分别为8.12,8.13 mm,且均出现于开挖线路与长江隧道交叉处,长江隧道东西线上浮最大值均未超过20 mm的规范限值;根据图8并采用Matlab进行函数曲线拟合,求得长江隧道东、西线纵向变形曲线的最小曲率半径分别为32804,32569 m,均大于15000 m,满足要求。

图8 开挖完成后长江隧道顶部竖向变形曲线
4.2 隧道管片上浮位移影响因素分析
为了更好的控制基坑开挖后下方既有隧道的上浮位移,为隧道变形控制提供更多的有效措施,我们将从加固封底厚度、加固封底宽度、加固土密度以及加固土弹性模量四个影响因素入手,对隧道的上浮位移进行分析。
(1)加固封底厚度
图9为长江隧道东、西线顶部最大上浮值与封底厚度的关系曲线;由图可知随着封底厚度的增大,隧道顶部最大上浮值呈减小趋势,同时减小速率先增大后减小,封底厚度由2 m增大至4 m时,上浮值减小幅度最大;以长江隧道东线为例,未加固时,隧道最大上浮值为10.6 mm,封底厚度取8 m时,隧道最大上浮值减小至8.12 mm,隧道最大上浮值平均减小速率为0.31 mm/m。

图9 隧道顶部最大上浮值随封底厚度变化曲线
(2)加固封底宽度
图10为封底厚度取8 m时,长江隧道东、西线顶部最大上浮值与封底宽度的关系曲线;由图可知随着封底宽度的增大,隧道顶部最大上浮值呈减小趋势,但曲线逐渐趋于平缓;以长江隧道东线为例,封底宽度取13.7 m时,隧道最大上浮值为8.12 mm,封底宽度增大至37.7 m时,隧道最大上浮值为5 mm,曲线割线斜率为0.13 mm/m;相比增大封底厚度,通过增大封底宽度的措施来减小隧道最大上浮值的效率较低。
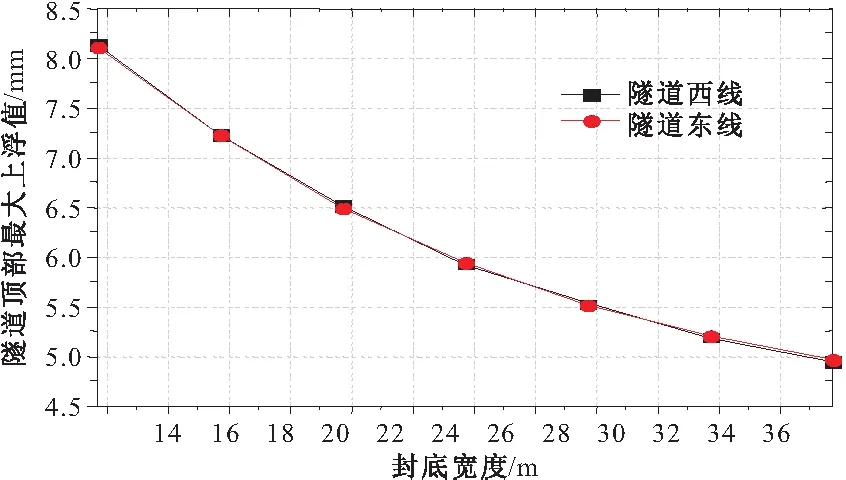
图10 隧道顶部最大上浮值随封底宽度变化曲线
(3)加固土密度
三轴搅拌桩满堂加固施工时,水泥掺入比宜为12%~20%,此情况下,水泥土的相对密度比原土约增大4%,若继续增大水泥用量,水泥土密度不会有明显增大。因此,本文加固土密度讨论范围定为1760~1830 kg/m3,其中1760 kg/m3为加固前土的密度。
图11为封底厚度取8 m、封底宽度取13.7 m时,长江隧道东、西线顶部最大上浮值与加固土密度的关系曲线。由图可知随着加固土密度的增大,隧道顶部最大上浮值几乎呈线性减小。以长江隧道东线为例,加固土密度取1760 kg/m3时(未加固),隧道最大上浮值为10.6 mm,加固土密度增大至1830 kg/m3时,隧道最大上浮值为8.12 mm。因此,采用增大加固土密度的方式来控制隧道上浮值,效果较为明显。

图11 隧道顶部最大上浮值随加固土密度变化曲线
(4)加固土弹性模量
图12为封底厚度取8 m、封底宽度取13.7 m时,长江隧道东、西线顶部最大上浮值与加固土弹性模量的关系曲线;由图可知,隧道顶部最大上浮值随着加固土弹性模量的增大略有减小,当加固土弹性模量从300 MPa增至450 MPa时,隧道结构最大上浮值仅减小0.06 mm,故增大加固土弹性模量对隧道结构上浮基本无影响。

图12 隧道顶部最大上浮值随加固土弹性模量变化曲线
5 结 论
本文以管廊基坑开挖对下方既有长江隧道变形的影响为研究背景,结合具体工程实例,以大型有限元软件ANSYS为分析工具。首先采用Winkler弹性地基梁理论对数值模型进行了验证,然后分析了基坑开挖后既有隧道变形的相关规律,最后研究了加固封底厚度、封底宽度、加固土密度以及加固土弹性模量对隧道竖向位移的影响规律,并得出了以下结论:
(1)长江隧道西线竖向位移曲线的数值解与理论解基本吻合,验证了数值模型的有效性。
(2)基坑开挖完成后,下方既有隧道顶部竖向位移呈现中间大、两边小的规律,并且最大位移出现在开挖路线与隧道交点附近。
(3)若采用基底加固控制隧道竖向位移时,优先选用增大封底厚度和加固土密度的措施;增大封底宽度,对于隧道竖向位移的控制效果并不明显,同时加固土的弹性模量对隧道顶部竖向位移基本无影响。

