基于TLE的弹道系数计算方法及应用分析

张炜，崔文，张育卫，刘兴，朱俊

1. 西安卫星测控中心，西安 710600 2. 宇航动力学国家重点实验室，西安 710043

大气阻力是低轨道空间目标所受的最主要非保守摄动力，其大小主要由两个因素决定：大气密度和空间目标的弹道系数。弹道系数B定义为大气阻力系数CD与面质比的乘积[1]，即B=CD×A/m，其中A为迎风面积，m为质量。

准确计算低轨目标的弹道系数对于开展大气密度研究、低轨目标轨道确定、再入预报等具有重要意义[2]。通常弹道系数被用作待估参数，与状态矢量一起，在基于测轨数据的轨道确定过程中求解[3]。除实际测量数据外，美国战略司令部于space-track网站发布的两行要素(Two Line Element，TLE)也是重要数据源，具有易获取、目标数量大、时间及空间覆盖广等特点，有独特的研究应用价值。任廷领等利用TLE反演热层密度并进行大气模型误差分析，反演过程中需要获得低轨目标的弹道系数“真值”[4-5]；Pardini等在机构间空间碎片协调委员会(Inter-Agency Space Debris Coordination Committee，IADC)再入联测中利用TLE进行再入预报，弹道系数计算也是其中重要一环[6-7]。

TLE中并没有弹道系数的直接信息，较为相关的是B*项，B*与真实的弹道系数B可近似为：B=12.741621B*[8]，但是此结果仍不够准确，与真实值之间存在不小的偏差[9]，获得较为准确的弹道系数仍需要运用其他方法。基于TLE的弹道系数计算方法主要可以分为两类：一类基于TLE生成伪测量数据，再利用伪测量数据重新确定轨道并解算弹道系数[10-12]，这类方法在实现上与基于实测数据的轨道确定过程并无本质上的区别；第二类通过比较TLE之间的轨道衰减计算弹道系数，大部分研究基于两组TLE进行计算[13-16]，弹道系数结果受TLE精度影响大，结果稳定性较差，实际应用中往往需要多次计算取结果均值。

本文主要研究第二类计算方法，即基于TLE轨道衰减计算弹道系数，考虑到TLE偏心率精度比半长轴精度低很多[17]，计算时仅考虑半长轴的衰减。介绍一种常见的基于两组TLE的直接计算法，分析了不同TLE间隔对结果精度的影响；提出一种基于多组TLE的迭代计算法，并从弹道系数计算结果、在再入预报中的应用等方面对这两种方法进行了比较，为实际应用提供依据。

1 弹道系数计算方法

1.1 基于两组TLE的直接计算法

大气阻力仅有长期作用效果，对于低轨目标其他摄动力的长期项与大气阻力相比基本可以忽略，因此可以通过平半长轴的衰减计算弹道系数。两组TLE之间平半长轴的变化认为由大气阻力引起[18]，大气阻力引起的半长轴变化可以表示为：

(1)

式中：a为半长轴；e为偏心率；n为平运动速度；p为轨道半通径；f为真近点角；r为径向距离；S和T分别为大气阻力的径向和横向分量，

(2)

式中：v为空间目标相对于大气的运动速度；ωE为地球转动速率；μ为地球引力常数；i为轨道倾角；ρ为大气密度，本文使用MSIS-90模型计算。将式(2)代入式(1)，简化后得到：

则两组TLE之间半长轴的衰减量ΔaTLE可以表示为：

因此，弹道系数计算：

(3)

其中：

Sang等给出的计算公式略有差别[14]，但计算原理基本一致。

1.2 基于多组TLE的弹道系数计算方法

直接计算方法的问题是弹道系数结果受TLE精度影响大，结果稳定性较差，实际应用中往往需要多次计算取结果均值。因此，提出使用最小二乘法对N(N≥3)组TLE进行弹道系数拟合，使半长轴的计算值与实测值之间的平均误差最小。假设已有N组连续的TLE，弹道系数计算过程如下：

2)设置弹道系数初值为B(0)=12.741 621B*，其中B*为第一组TLE的大气阻力项。

3)从第一组TLE根数开始对Gauss型摄动方程进行轨道积分，考虑的摄动力包括地球非球形J2项、J3项和大气阻力。

4)若积分结束时刻与第k组TLE历元时刻之差小于积分步长的一半，则计算半长轴计算值与实测值之差Δak及半长轴对弹道系数的偏导数∂ak/∂B，否则继续下一步积分。

5)第N条根数计算结束后，计算弹道系数修正值：

(4)

6)若ΔB(j)小于收敛阈值，则计算结束，否则对弹道系数进行修正：

B(j+1)=B(j)+ΔB(j)

返回步骤3)开始第j+1次迭代。

由于计算过程采用平根数作为轨道形式，不含周期项，因此轨道积分可采用半分析方法，步长取为轨道周期的整数倍，以提高计算效率。此外，计算过程中可以根据半长轴的残差情况识别误差较大的TLE并重新编辑数据资料，进而提高结果精度。

2 结果与分析

2.1 弹道系数结果

选择NORAD编号为00694和42821的两个目标作为算例目标进行验证。其中，00694是一个外形为圆柱体的火箭箭体，近地点轨道高度约463 km，TLE选用的时间区间为2014年2月—2015年1月，期间F10.7指数90～200，太阳活动整体处于中等水平；42821是一个尺寸约为10 cm的立方体卫星，质量约1 kg，目前已经陨落，TLE选用的时间区间为2018年5月—2019年5月，期间F10.7指数65～80，太阳活动水平极低。两个目标的基本信息如表1所示。

表1 两个算例目标的基本信息

图1和图2所示分别是00694和42821目标的弹道系数序列，表2列出了两个目标弹道系数的统计结果。使用迭代法计算时，N取值为6，即基于6组TLE计算弹道系数，使用直接法时TLE选择的是该TLE序列的第一组和最后一组，使两种方法所用TLE的时间跨度一致。根据文献[14]的分析结果，1980—2011年间00694的弹道系数均值为0.014 81 m2/kg，与本文结果仅差约2%；42821的理论弹道系数约为0.021 m2/kg，与本文结果也极为接近，证明了两种方法的准确性。对比两种方法的弹道系数均值，发现差异极小。基于两组TLE的弹道系数均值分别为0.014 48 m2/kg和0.019 81 m2/kg，基于多组TLE的弹道系数均值分别为0.014 49 m2/kg和0.019 82 m2/kg。认为长期效果方面两种方法并无差别，且两种方法的弹道系数结果在变化趋势上基本一致。但是基于多组TLE的弹道系数结果稳定性略好，其原因是基于两组TLE计算时TLE误差直接被弹道系数吸收，弹道系数结果受TLE半长轴精度影响较为明显。较为典型的是图1和图2中方框标注的结果，明显误差偏大。需要说明的是，两个算例目标所用TLE均为根据平运动平滑过滤后的结果，已经剔除大部分误差较大TLE，若使用原始数据进行计算，基于多组TLE迭代计算的优势将更明显。

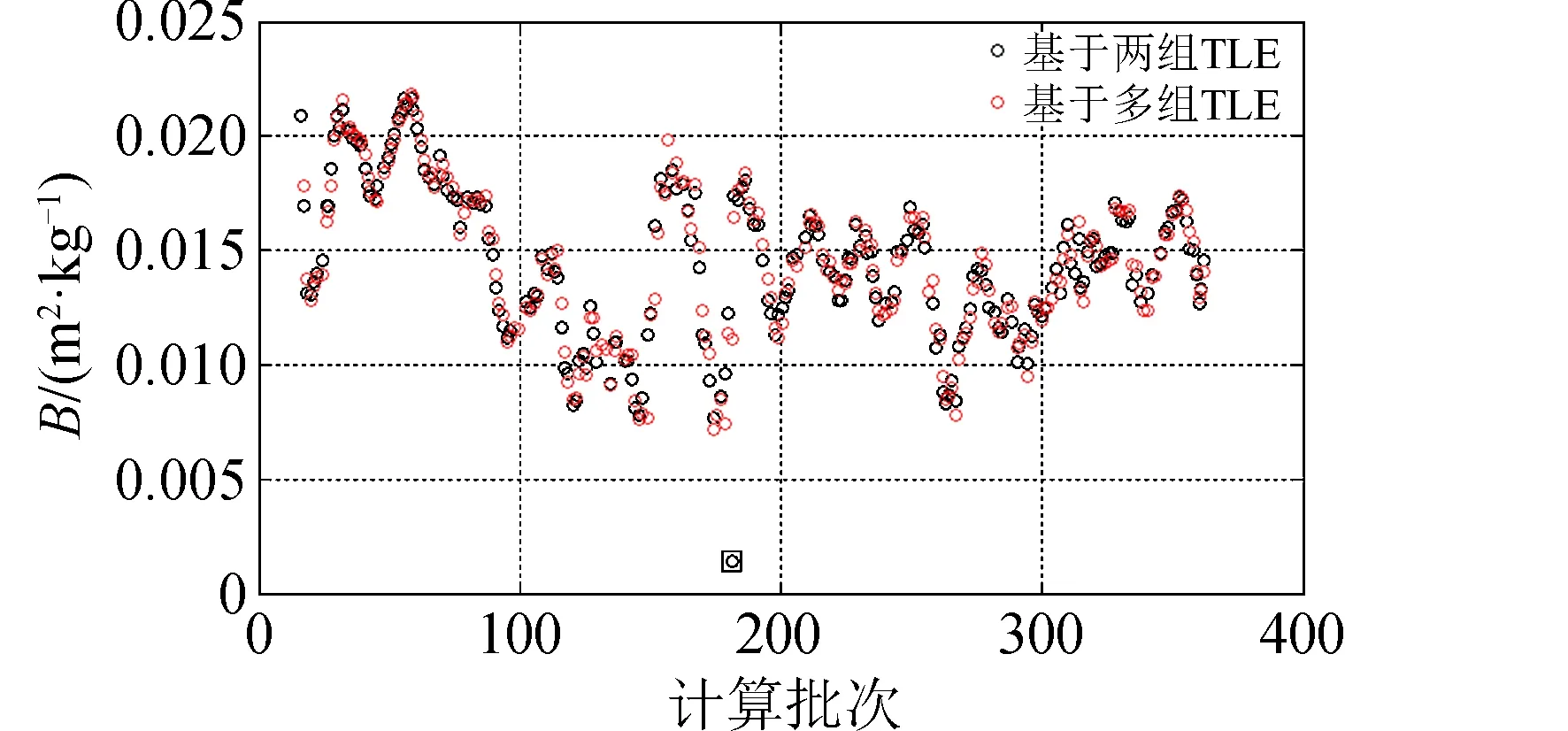
图1 00694的弹道系数结果Fig.1 Ballistic coefficient results of 00694

图2 42821的弹道系数结果Fig.2 Ballistic coefficient results of 42821

m2/kg

2.2 用于再入预报的比较

确定空间目标的弹道系数是再入预报的关键步骤，弹道系数结果的准确性直接影响再入预报结果的精度。本节将讨论两种弹道系数计算方法用于再入预报时的效果。进行再入预报时，基于最新两组或多组(取值为6)TLE计算弹道系数，并使用SGP4/SDP4模型直接计算最后一组TLE在其历元时刻的状态矢量，作为再入预报的初始轨道。最后基于初始轨道和弹道系数结果，采用数值积分的方法进行轨道外推直到轨道高度低于80 km，积分结束时刻即为再入时刻。考虑的摄动项包括地球非球形引力、大气阻力摄动、太阳光压摄动和日月引力摄动。

使用再入预报相对误差δ评估再入预报的精度，再入预报相对误差δ为:

式中：treal为再入目标的实际再入时间；tpred为预报的再入时间；t0为进行再入预报时使用轨道的历元，本文中即为两组或多组TLE中最后一组TLE的历元。

以42821目标为例，取最后一次计算结果为实际再入时间，利用两种方法的弹道系数结果进行再入预报的精度情况如图3所示。可以看到，基于两组TLE的最大预报误差为53.2%，平均误差约12.2%，而基于多组TLE的最大预报误差为39.8%，平均误差约10.6%。总体而言，无论是预报精度还是预报结果的稳定性，基于多组TLE的再入预报方法均有较大优势，原因就是基于多组TLE的弹道系数结果具有更好的稳定性。

图3 42821目标的再入预报结果Fig.3 Re-entry prediction results of 42821

但是基于多组TLE的弹道系数结果用于再入预报时并非一直最优。受方法本身特点的限制，使用多组TLE时数据区间不可能太小，而两组TLE的选择却灵活许多。考察了随机28个再入目标再入前10天起两种方法的精度情况，结果如图4所示。其中，两组或多组TLE均为计算时获取的最新TLE结果，即使用直接法时TLE选用的是迭代法所用TLE序列中的最后两组。黑色部分为基于两组TLE预报精度较优的目标个数，红色部分为基于多组TLE预报精度较优的目标个数，比较时各再入目标的实际再入时间均取自space-track网站发布的最终再入信息。可以看到，当距离目标再入不足1天，基于两组TLE的弹道系数结果较优的次数明显多于基于多组TLE；当距离目标再入大于1天，两种方法的优劣次数基本相当。其原因是使用直接法计算时，由于选择的是最新的两组TLE，数据区间较短，弹道数据结果与数据弧段内再入目标的轨道数据(即TLE)情况、空间环境情况等形成良好的耦合系统，可以更好地反映再入目标短期轨道衰减特性。另外，在计算过程中发现，当临近再入，基于多组TLE拟合弹道系数时迭代次数明显增加，甚至可能出现不收敛的情况。

图4 28个再入目标再入前10天起两种方法的精度情况Fig.4 Re-entry prediction results for 28 test objects in the last 10 days

综合以上分析，在中长期再入预报中，建议采用基于多组TLE的弹道系数计算方法，以获得更稳定的再入预报结果；当距离目标再入不足1天，建议采用基于两组TLE的弹道系数计算方法，以获得更高精度的再入预报结果。

2.3 TLE历元间隔对结果的影响

假设两组TLE之间半长轴衰减的误差为Δaε，实际衰减值为Δat，根据式(3)有：

式中：Bc为弹道系数的计算值；Bt为真实值。显然，TLE间隔越大或运行高度越低，大气阻力的累计效应λ越大，同等半长轴误差引起的弹道系数误差越小。

同样以NORAD编号为00694和42821的两个目标为例，验证使用基于两组TLE直接计算弹道系数时TLE间隔对结果的影响。两个目标均选择2018年的TLE作为数据源，使分析过程二者经历的空间环境一致。00694目标2018年的弹道系数均值较第2.1小节分析结果有较大变化，仅为0.009 6 m2/kg。一方面是因为太阳活动水平极低情况下大气密度模型的误差增大[19]，另一方面空间目标的大气阻力系数较太阳活动高年也有所降低[20]。42821目标的弹道系数均值与第2.1小节一致，取为0.019 8 m2/kg。TLE间隔分别取为0.25 d、0.5 d和1 d。两个目标弹道系数的相对误差分别如图5、图6所示。

图5 00694不同TLE间隔的弹道系数结果Fig.5 Ballistic coefficient results of 00694 based on different TLE intervals

图6 42821不同TLE间隔的弹道系数结果Fig.6 Ballistic coefficient results of 42821 based on different TLE intervals

对比0.25 d、0.5 d和1 d三种间隔，00694目标的最大误差分别为290%，223%和123%，标准差分别为69%，49%和34%；42821目标的最大误差分别为85%，56%和56%，标准差分别为20%，16%和15%。可以看到：1)TLE间隔越小，弹道系数误差越大，结果精度的稳定性也更低；2)随着轨道高度降低，相同间隔TLE的弹道系数误差减小(00694的平均高度约为900 km，42 821的平均高度约为370 km)；3)TLE间隔的增大对42821弹道系数结果的改进效果明显较弱，TLE间隔为0.5 d和1 d两种情况的最大误差和标准差已经极为接近。其原因与前文分析一致，即在相同时间间隔内，轨道高度越低的目标所受的大气阻力累积效应越大，同等半长轴误差引起的弹道系数误差越小。因此，若使用基于两组TLE直接计算弹道系数，应根据空间目标的轨道情况确定TLE间隔，当空间目标的轨道高度较高，两组TLE之间的间隔应偏大，当空间目标的轨道高度较低，TLE的间隔可以相应缩小。

3 结束语

本文研究了两种基于TLE的低轨空间目标弹道系数计算方法。介绍了一种常见的基于两组TLE的直接计算法，提出了一种基于多组TLE的迭代计算法，并对两种方法的应用效果进行了分析。得出以下结论：1)从长期效果看，两种方法弹道系数结果的均值和变化趋势基本一致，但是基于多组TLE的弹道系数计算方法具有更好的稳定性。2)用于再入预报时，在中长期预报中建议采用基于多组TLE的弹道系数计算方法，以获得更稳定的再入预报结果；当距离目标再入不足1 d，建议采用基于两组TLE的弹道系数计算方法，以获得更高精度的再入预报结果。3)若基于两组TLE计算弹道系数，当空间目标的轨道高度较高，两组TLE之间的间隔应偏大，当空间目标的轨道高度较低，TLE的间隔可以相应缩小。

本文的研究结果可为实际应用中弹道系数计算方法和相关参数的选择提供依据。后续可在使用最小二乘法迭代计算弹道系数时如何改进轨道结果，及轨道改进后对轨道预报精度的影响等方面开展研究。