高等数学中求极限方法总结
2020-06-23 09:31杨小迪
文理导航 2020年20期
杨小迪
【摘要】极限思想是微积分的基本思想,是高等数学中的一系列重要概念,如函数的连续性、导数以及定积分等,都是借助极限来定义的。如果要问高等数学是一门什么学科,那么可以概括地说:“高等数学就是用极限思想来研究函数的一门学科,并且计算结果误差小到难以想象,因此可以忽略不计。”
高等数学是理工科院校最重要的基础课之一,极限是高等数学的重要组成部分。求极限方法众多,非常灵活,给函授学员的学习带来较大困难,而极限学的好坏直接关系到高等数学后面内容的学习。下面先对极限概念和一些结果进行总结,然后通过例题给出求极限的各种方法,以便学员更好地掌握这部分知识。
【关键词】极限;高等数学;方法


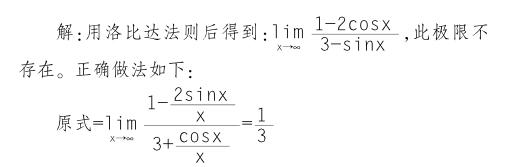
【參考文献】
[1]同济大学数学系.高等数学(上册)[M].高等教育出版社,2014
[2]同济大学数学系.高等数学(下册)[M].人民邮电出版社,2016
(郑州商学院,河南郑州451200)
猜你喜欢
科学导报·学术(2020年6期)2020-03-07
少年文艺·我爱写作文(2019年9期)2019-11-04
试题与研究·教学论坛(2017年14期)2017-04-10
黑龙江教育·理论与实践(2016年9期)2016-05-14
现代情报(2016年7期)2016-05-14
课程教育研究·学法教法研究(2016年7期)2016-04-26
新课程·下旬(2015年10期)2015-10-21
国学(2014年3期)2014-03-20

