不规则实体堰坝流场及应力场耦合分析

丁少超，黄 青

(浙江省水利水电技术咨询中心，浙江 杭州 310020)

千百年来堰坝作为一种壅水建筑物，主要用于灌溉，是古代先民治水历史中的重要智慧结晶[1-2]。它通过拦截水流，抬高水位来满足引水灌溉的需求，同时在一定程度上也可对整个河道的坡降进行调整，以起到巩固泥沙的作用；另一方面它还能够改善和治理区域内的生态环境和生态质量，从而促进人与自然的和谐发展[3]。在全国中小河流中有着不计其数的堰坝，其中多为实体固定堰。近年来较多堰坝并未达到使用年限就发生局部冲毁甚至整体破坏的现象[4-5]。因此，在设计阶段完善堰坝流场分析与稳定性分析显得尤为重要。

目前堰坝稳定计算主要采用结构静力学的方法，在堰体稳定分析时常选取堰坝剖面进行单宽计算，而不规则堰坝各剖面均不同，采用该方法无法准确反映堰坝及基础受力情况[6]。此外，在受力分析时常将堰体、基础和水体作为单独对象，没有考虑结构之间的相互影响以及应力、变形的分布情况。

近些年，随着计算机辅助工程(CAE)软件的完善，有限元法在水利工程领域已经得到广泛应用，但考虑自由表面外部流场与应力场耦合的堰坝稳定分析还较为欠缺[7-16]。本文基于ANSYS Workbench仿真平台对不规则实体堰进行流固耦合仿真计算。首先，考虑结构之间的相互作用关系，建立堰坝和基础的材料模型；然后，将模型导入ANSYS CFX中引入气液两相流来模拟堰坝的流场以及水压力分布；最后，将流体计算结果耦合到结构力学分析中完成堰坝的应力及变形分析。

1 工程概况

设计中的堰坝位于浙江省东阳市南江水库下游湖溪镇境内，堰坝宽77.3 m，长15 m，消力池长度为11.5 m，堰坝底部最低点高程为133.52 m，堰顶高程为139.5 m，设计20年一遇洪水位高程为141.1 m。堰坝上下游齿墙深入弱风化粉砂岩0.5 m，堰坝上游与消力池下游设有抛石防冲槽。堰体采用金包银结构，堰体内为C20埋石混凝土，外部采用50 cm厚C20混凝土。消力池为C25F50钢筋混凝土结构。基础材料从上至下分别为含细粒土砾、强分化粉砂岩和弱风化粉砂岩。图1给出堰坝的整体模型和材料分区情况。

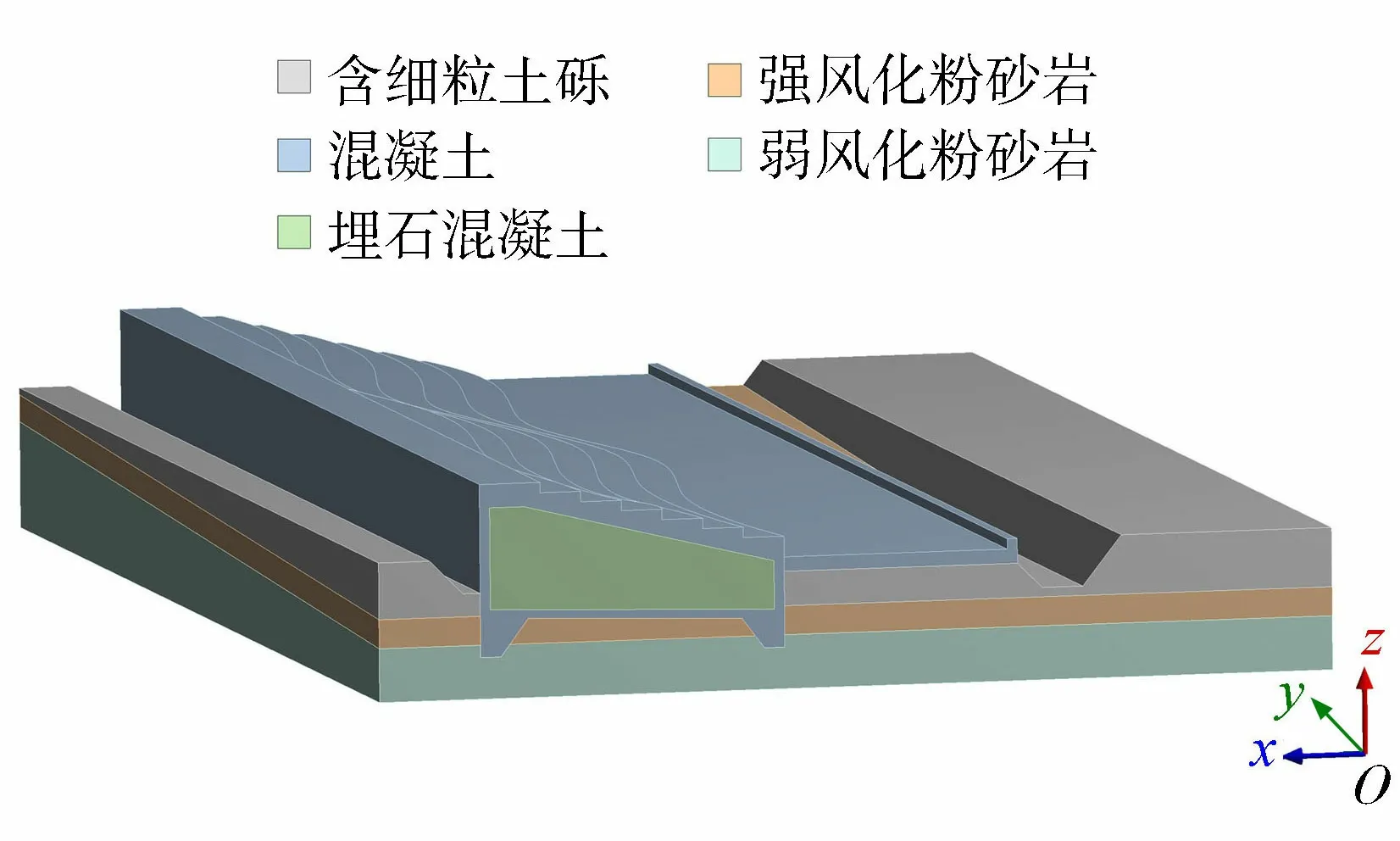
图1 堰坝模型和材料分区

由于堰坝左右两岸基岩面高程相差较大，弱风化粉砂岩高程相差1.6 m，因此，堰坝底部高程需根据基岩面进行调整，整体为左高右低的倾斜面。堰坝底部高程的改变将会造成堰体内部结构的变化，而采用传统的断面单宽进行计算显然并不准确。本文通过建立各材料的三维模型并设置对应的材料参数以及材料之间的接触关系，来模拟实际工程中堰坝的情况。

2 基本假定及控制方程

2.1 基本假定

数学模型建立时采用如下基本假定：①水体为不可压缩黏性流体；②堰体为具有小变形理想弹性体；③水体与堰体接触界面上法向位移是相等的，即水体与堰体在法向不发生直接脱离，只沿切向发生相对滑动。

2.2 基本方程

流固耦合中，控制方程包括流体控制方程和结构运动方程。

2.2.1流体控制方程

求解自由边界问题常采用拉格朗日、欧拉和任意拉格朗日-欧拉(ALE)3种方法[17]。流体的控制方程建立在拉格朗日法下可较好地模拟流体自由面和边界情况，但流体变化较大时会导致网格畸变严重，求解不收敛。采用欧拉法计算时收敛情况较好，但由于网格不允许变形，难以模拟流体的变化情况。ALE坐标系为拉格朗日坐标系和欧拉坐标系的组合，独立于材料和有限元网格区域的坐标系统，有限元网格和材料允许在该坐标系下任意移动[18]。因此，本文采用ALE法模拟堰坝水体自由面与流固耦合面的流速、流线及水压力的分布情况。在ALE坐标系下求解流体的控制方程由连续方程和动量方程组成[19-21]：

(1)

(2)

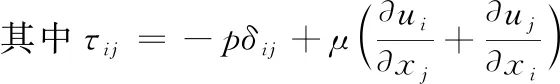
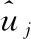
2.2.2结构运动基本方程

对于弹性小变形结构，在xi坐标中的运动方程为

(3)

(4)

式中：σij为应力；εij为应变率；Fsi为固体体积力在xi方向上的分量；ρs为固体密度；si、ai分别为xi方向上的位移分量和加速度分量。

2.2.3流固耦合中的有限元方程

假设耦合体系的求解向量为X=(Xf,Xs)，其中Xf和Xs分别为定义在水体和结构节点上的求解向量。将流体方程和结构方程统一到刚度矩阵中，则流固耦合体系的有限元方程可写为

(5)

式中：Aff、Bf分别为流场的系统矩阵、外部作用力矩阵；Ass、Bs分别为固体区域的系统矩阵、外部作用力矩阵；Asf、Afs为流固耦合矩阵；ΔXf,k、ΔXs,k分别为Xf、Xs在第k个迭代步的变化量。

2.3 边界方程

在求解堰坝表面流时，流体域是由空气和水体组成的两相流，初始条件下考虑流体域自由面气体的体积分数为1，即自由面为气相。入口边界条件为流体沿竖直方向的流速方程且入口水体的体积分数为1，入口高程为堰上水位高程，入口为液相；出口边界条件为水体自由面相对压强为零，压强沿竖直方向由静水压强公式控制，出口为气液两相边界。通过两相流基本方程，求解水体自由面，即计算出水体的体积分数为1的临界面。同时在计算流固耦合面上流体相对于固体的运动关系时，须满足运动学和动力学两种边界条件[22-23]。

气液两相流动基本方程为

(6)

式中：vk、Vk、Ak、nk分别为第k相(k=1表示液相，k=2表示气相)的速度、体积、表面面积、表面的单位外法向矢量；ρ2为气体密度。

运动学边界条件为

(7)

式中：us、vs、ws分别为水体自由面沿x方向(坝宽方向)、y方向(坝轴线方向)、z方向(竖直方向)的速度分量。

动力学边界条件为

p0=p气z=h(x,y,t)

(8)

式中：p0为流固耦合面上的压强；p气为气体压强。

流体与固体接触面会发生相互作用，流体会使堰坝发生应变，而堰坝变形又会改变流体形态，因此在流固接触面上需满足作用力平衡(动力学条件)和位移一致性(运动学条件)：

(9)

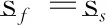
(10)

3 计算模型

3.1 计算工况

分2种工况进行计算：①设计洪水位工况，堰上水位高于堰顶1.6 m，堰上流速1.38 m/s，荷载组合为自重、水重、静水压力、扬压力；②常水位工况，堰上水位高于堰顶0.3 m，堰上流速0.34 m/s，荷载组合为自重、水重、静水压力、扬压力。

3.2 网格模型

流体模型和堰坝模型建立后，根据求解顺序先对流体模型进行网格划分。在求解堰坝流固耦合问题时忽略热传导作用，因此，在对流体进行网格划分时可先抑制堰坝模型，定义流体与堰坝接触面，根据流场求解器选择对应的流体网格划分方式。此外，由于需要分析接触面上的流场和水压力分布，因此考虑对接触面网格进行加密处理。流体全局网格单元尺寸控制为0.5 m，流体与固体接触面网格单元尺寸控制为0.3 m。同时对堰顶水深处局部网格进行加密处理，设计洪水位工况下，局部接触面尺寸设置为0.15 m，常水位工况下，局部接触面尺寸设置为0.1 m。图2(a)给出设计洪水位工况的流体计算网格，其中单元节点数为548 899，网格单元数为2 947 440。图2(b)给出常水位工况的流体计算网格，其中单元节点数为431 331，网格单元数为2 215 298。

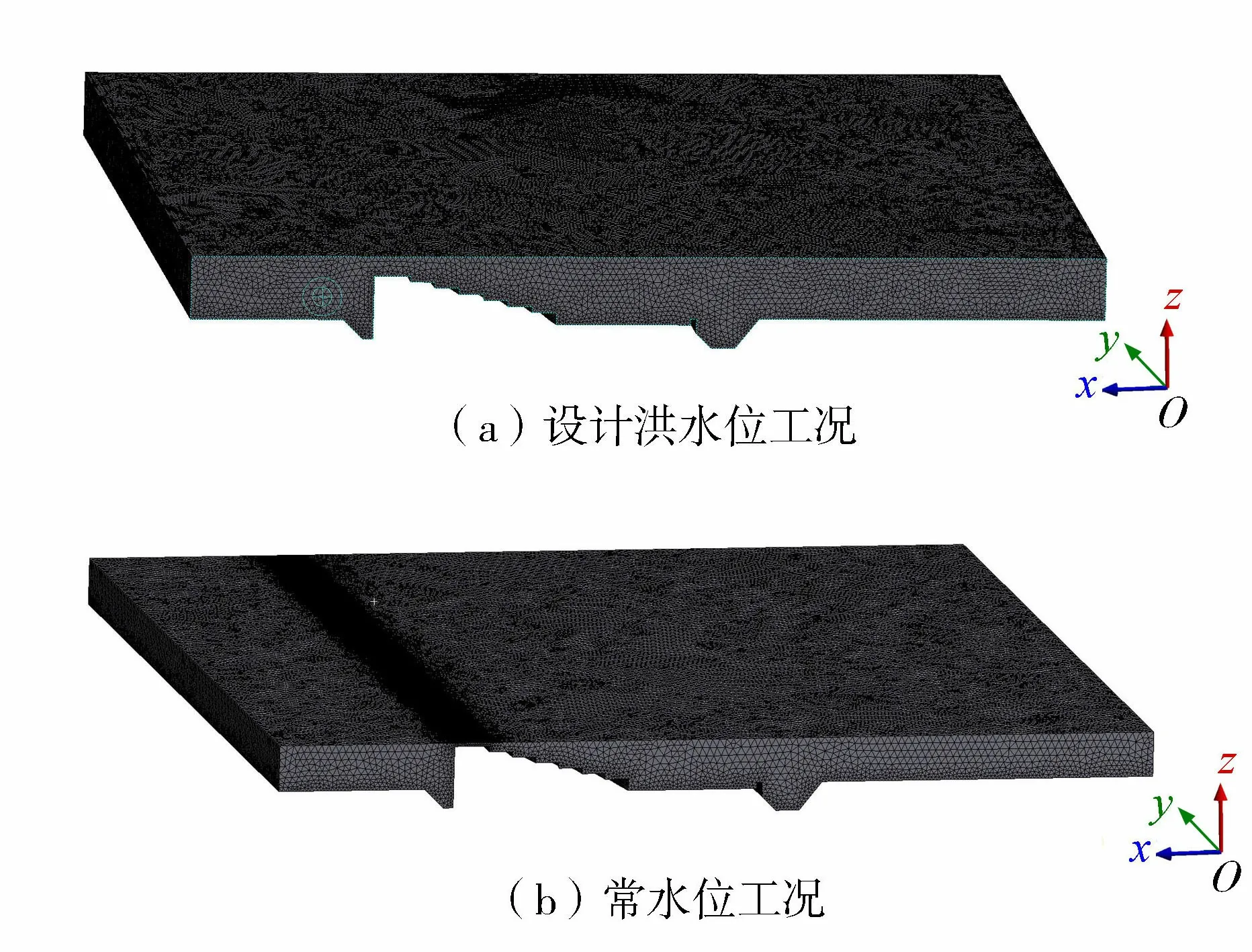
图2 流体计算网格

在流场计算完成后进行堰坝结构稳定分析，需对堰坝及基础模型进行网格划分。在进行流固耦合分析时流体与固体接触面会发生应力传递，因此需要加密流体与固体接触面的网格，具体通过设置固体接触面网格尺寸和膨胀层来完成。在固体表面设置3层膨胀层，增长率为1.2。堰坝外层混凝土结构采用四面体网格划分，堰体、消力池和基岩采用六面体网格划分，全局网格尺寸控制为0.5 m。图3给出堰坝及基础的整体网格模型，其中单元节点数为1 552 462，网格单元数为501 523。

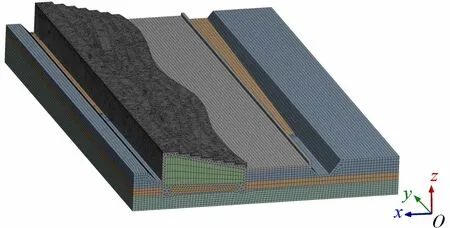
图3 堰坝及基础网格模型

3.3 计算参数

堰坝及基础材料力学计算参数见表1。

表1 材料力学计算参数

4 计算结果分析

4.1 流场分析

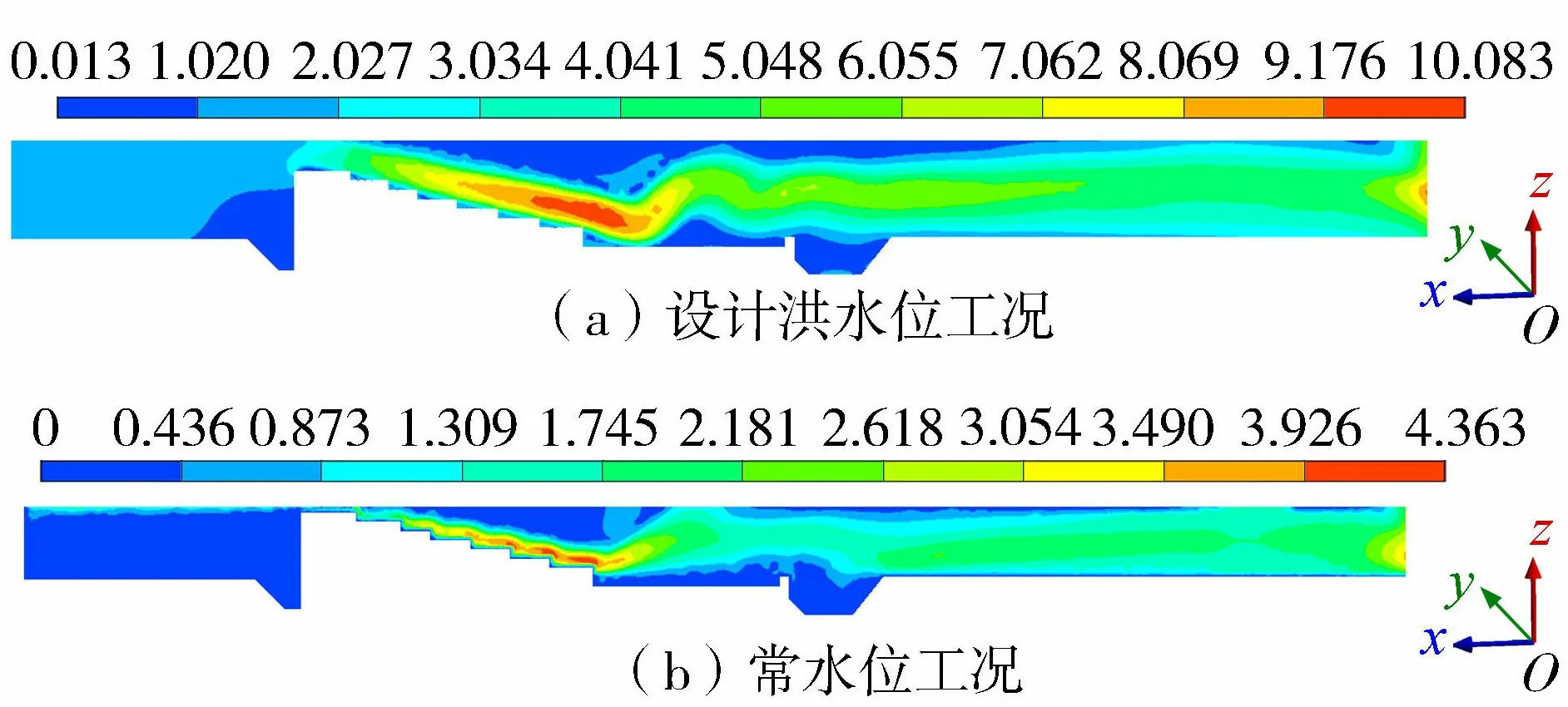
图4 堰坝纵剖面流速分布(单位：m/s)

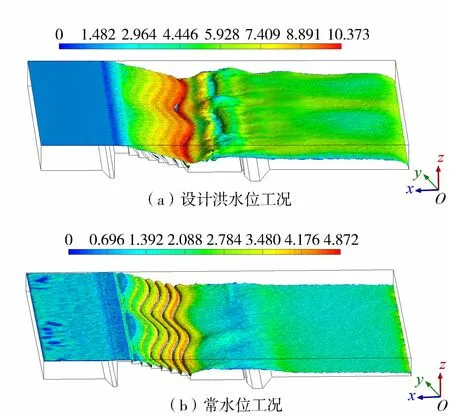
图5 自由表面流速分布(单位：m/s)

图4给出堰坝纵剖面流速分布。由图4可见，堰坝上的水体由上游至下游势能转化为动能，水体的流速由初始值逐渐增大，并在消力池内发生水跃，随后流速下降。对比图4(a)与图4(b)可见，相较于低流速水流，高流速水流发生掺气的现象明显，能量消散较快，相应流速变化梯度也较大。由于水流阻力，液体流速从固体壁面上零值增加到主流流速，形成一定的流速梯度。因此，水体沿堰坝下泄时最大流速发生在水体内部。需要注意的是剖视图中的流速涵盖了水气混合的流速分布。图5为相对压强为零的自由表面流速分布。该图可以直观地表现出流体沿堰坝下泄时的特性。从图5(a)可以看出，堰坝下游水深小于共轭水深，发生远离水跃，且在堰坝曲线凹侧共轭水深大于其他位置处。

4.2 应力分析

在进行堰坝稳定分析时，需导入流体分析的计算结果进行耦合。图6为耦合后堰坝及基础表面的水压强分布，可以看出模拟的水压强分布与水力学公式计算值基本一致。

堰坝及基础最小主应力分布如图7所示，其中拉应力为正值，压应力为负值。由图7可以看出，压应力自上而下递增，设计洪水位工况下堰坝在含细粒土砾层、强分化粉砂岩层和弱风化粉砂岩层的压应力最大值分别为55 kPa、155 kPa和180 kPa，常水位工况下各层压应力最大值分别为45 kPa、140 kPa和171 kPa，均能满足各层地基承载力要求。

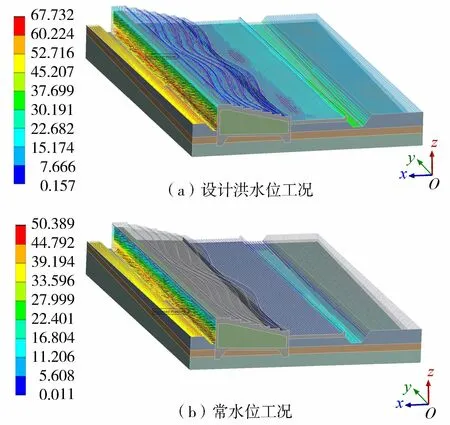
图6 水压强分布(单位：kPa)

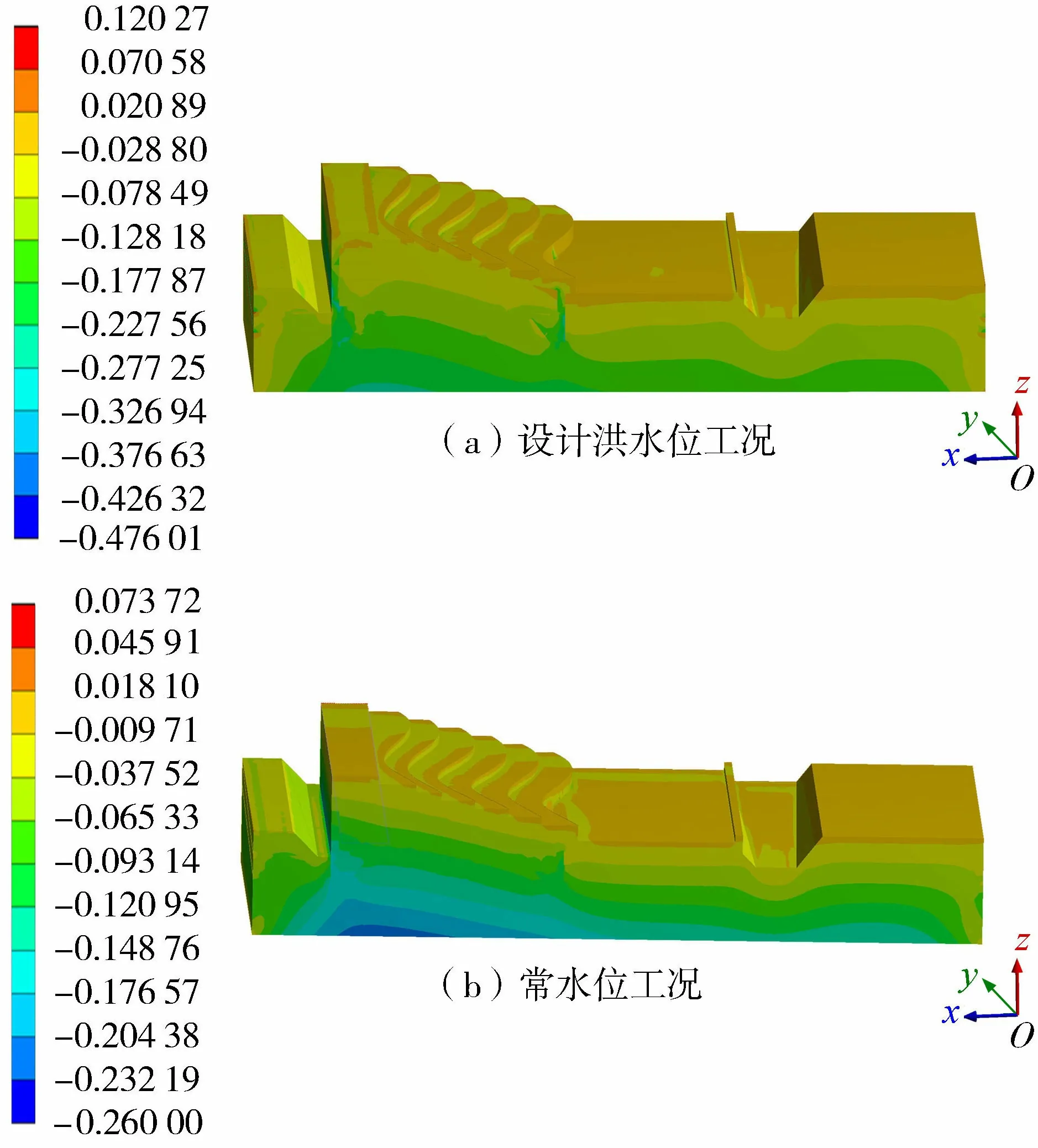
图7 最小主应力分布(单位：MPa)

图8给出两种工况下堰坝剖面最小主应力分布，设计洪水位和常水位工况下堰坝基底面压应力最大值与最小值之比分别为1.20和1.28，均能满足规范要求。

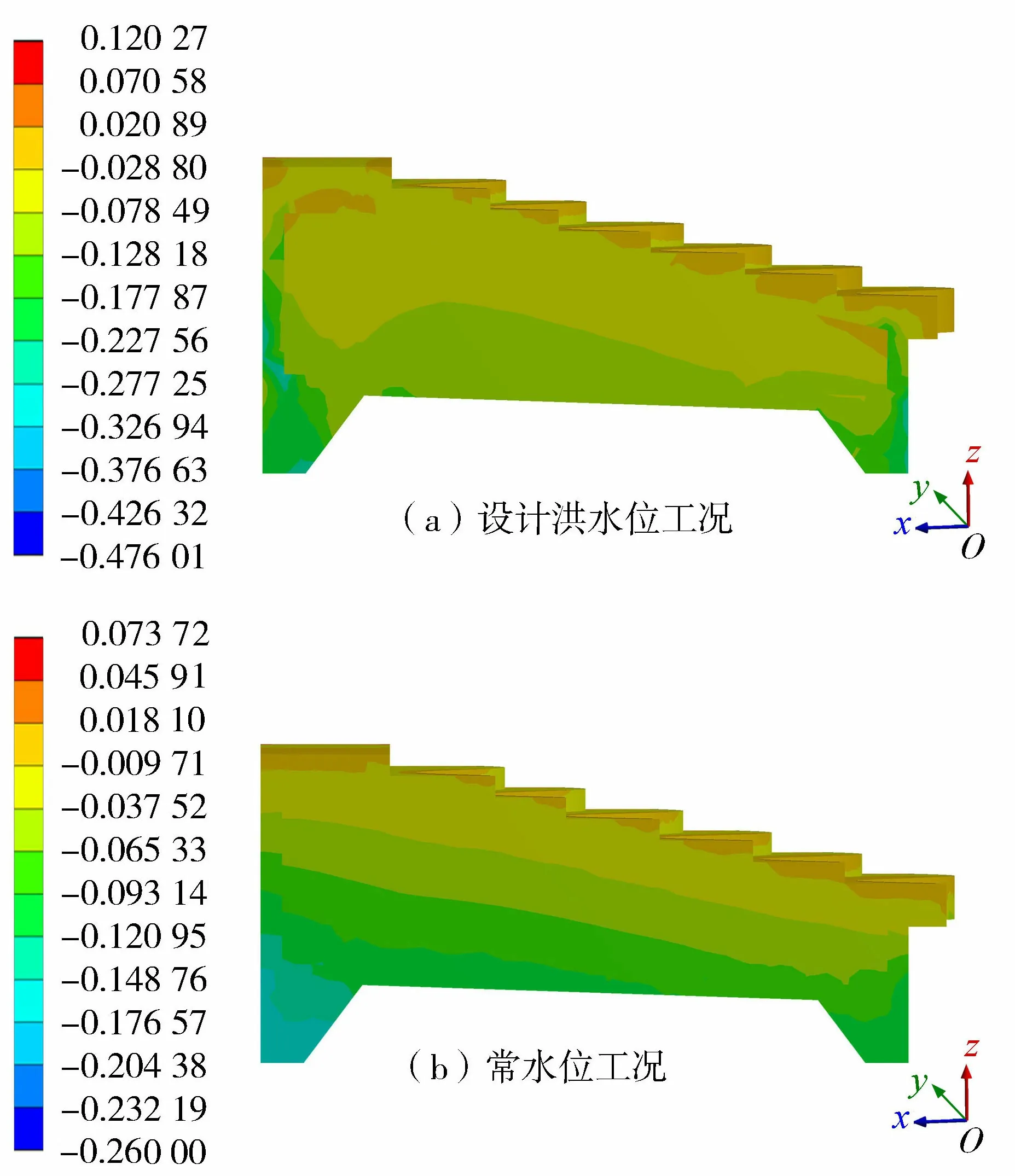
图8 堰坝剖面最小主应力分布(单位：MPa)

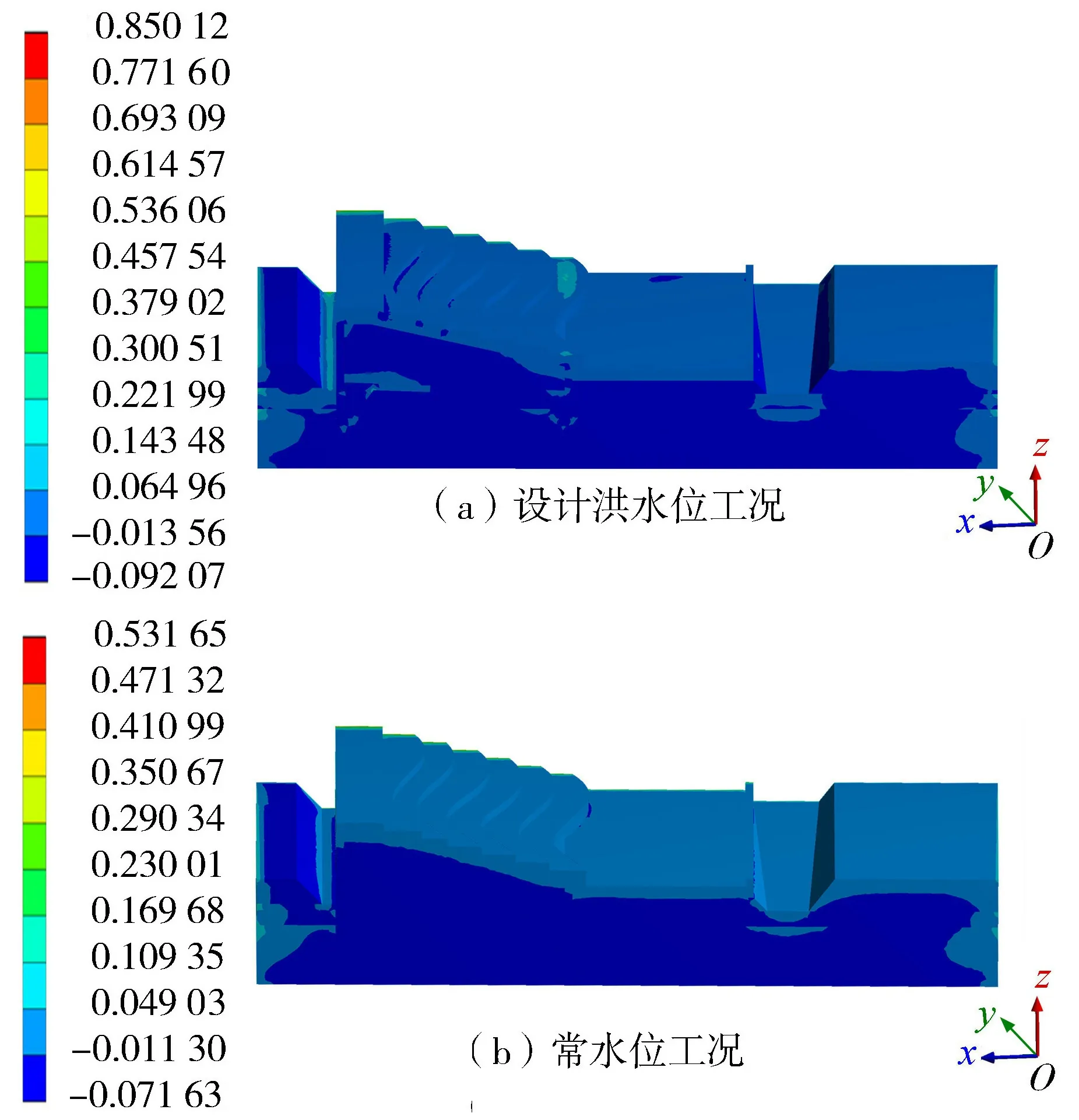
图9 最大主应力分布(单位：MPa)

堰坝最大主应力分布如图9所示，可以看出堰体内部最大主应力值为负，说明堰体内部未出现拉应力。在设计洪水位工况下，堰坝表面出现少量拉应力，主要分布在堰坝最后一个台阶与消力池内。此外，由于堰坝两岸受到位移约束的影响，使得拉应力极值出现在堰坝与两岸挡墙交接面上。堰坝表面和堰坝上下游位置处挡墙均为C20混凝土材料，抗拉强度为1.3 MPa，模拟的拉应力极值小于混凝土的抗拉强度。

4.3 变形分析

位移约束考虑基础在弱风化基岩面下1.5 m处不发生相对位移，将堰坝与挡墙结构视为整体进行分析，堰坝模型上下游边界视为无穷远，相对位移为零。堰坝整体变形分布如图10所示，可以看出整体变形自上而下递减，变形极值出现在上游拋石防冲槽右岸，由材料模型可看出该处为含细粒土砾，右岸至左岸基岩面逐渐上升，整体变形也逐渐变小，符合材料模型的变形规律。

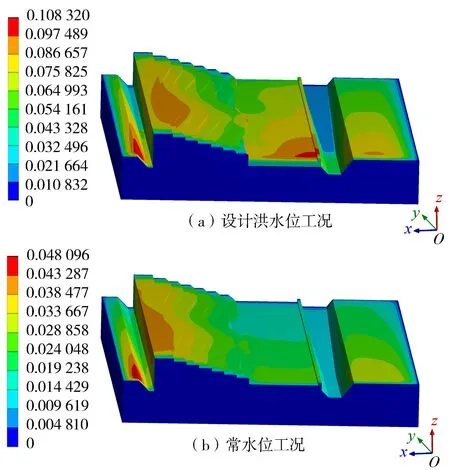
图10 整体变形(单位：mm)

图11给出堰坝和基础沉降变形，负号代表变形方向。设计洪水位工况下最大竖向变形为0.10 mm，常水位工况下最大变形为0.048 mm，远小于规范允许的地基最大沉降量。最大沉降均发生在含细粒土砾层，与实际情况相符。

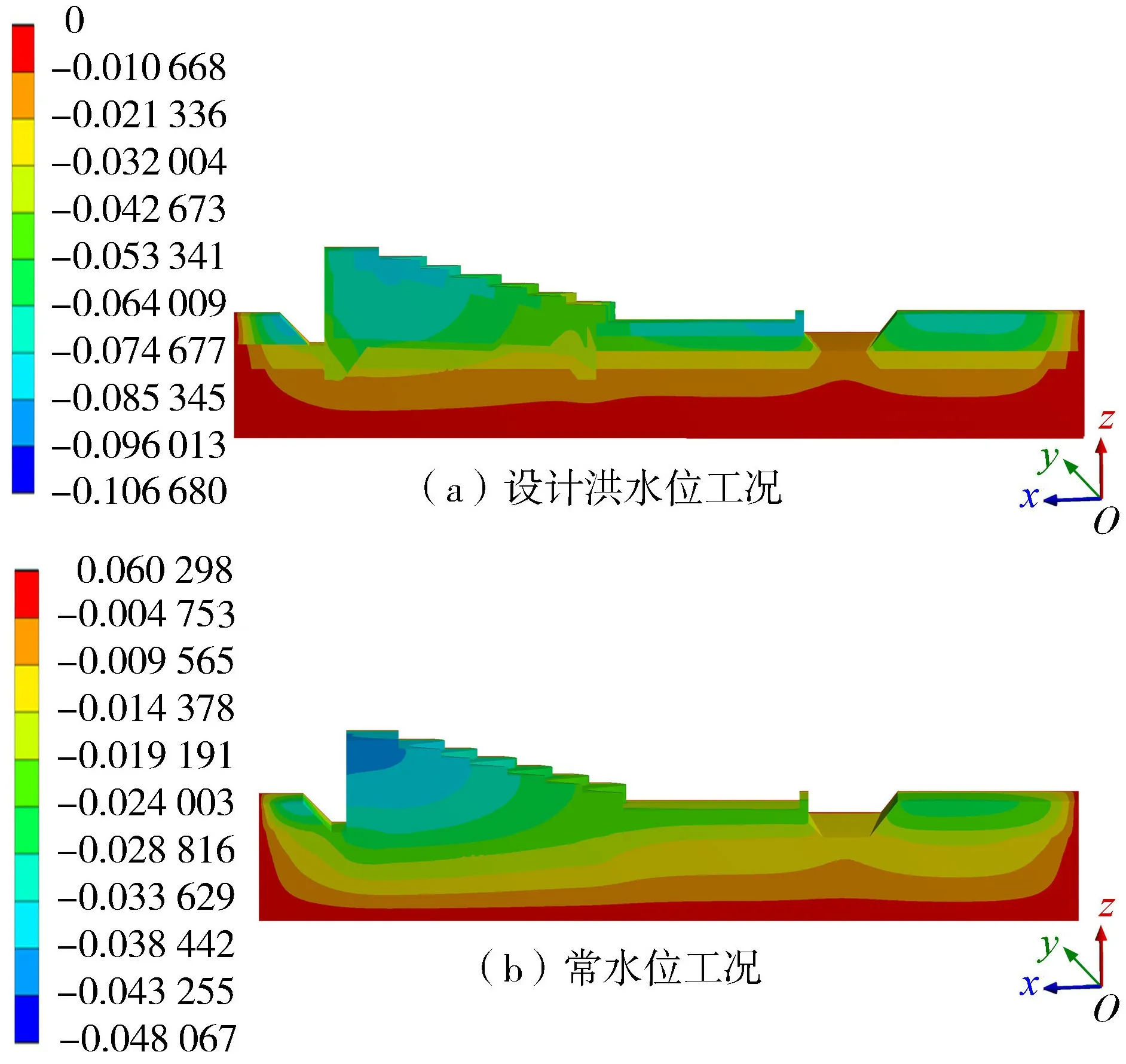
图11 沉降变形(单位：mm)

5 结 论

a. 基于ANSYS CFX的有限体积法求解流场，通过引入气液两相流求解堰坝的表面流场和水压力。计算结果表明该方法可有效解决自由表面外部流动问题。

b. 设计洪水位工况下堰坝下游水深小于共轭水深，发生远离水跃，且在堰坝曲线凹侧共轭水深大于其他位置处，因此堰坝下游需设消能工。

c. 设计洪水位与常水位工况下堰坝在含细粒土砾层、强分化粉砂岩层和弱风化粉砂岩层的压应力均能满足各层地基承载力要求，且堰体内部未出现拉应力。

d. 堰坝及基础变形计算结果合理，且能很好地反映堰体与基础非连续性的变形情况。两种工况下最大竖向变形小于规范允许的地基最大沉降量，且沉降极值均发生在含细粒土砾层，与实际情况相符。