钢管桩码头地震易损性分析的单自由度模型*

高树飞，冯云芬

(聊城大学建筑工程学院，山东 聊城 252000)

钢管桩由于水平承载力高，而且弹性和韧性较好，在全直桩码头中得到广泛应用。虽然钢管桩码头的承载力和延性相比同等尺度的混凝土桩码头要高，但是在强震作用下仍会发生较大破坏。例如，1995年的日本Hyogoken-Nanbu地震造成神户港Takahama码头的钢管桩发生较大破坏，钢管桩在桩帽和入土部分处均出现较大的弯曲变形，致使码头运行中断[1]。因此，对钢管桩码头进行合理的抗震设计和评估，对于港口的防灾和减灾具有十分重要的意义。传统的高桩码头的抗震设计方法[2]，无论是基于力的方法，还是基于位移的方法，均是考虑确定性评估码头的抗震性能，无法考虑不确定性(包括地震动不确定性和结构不确定性)对码头抗震性能的影响，因此近年来从概率角度分析评估码头抗震性能正逐渐引起研究人员的关注，而地震易损性分析方法则是最常用的概率评估方法。该方法通过计算结构在不同地震动强度下发生不同破坏状态的条件概率，从宏观角度描述地震动强度对结构破坏的影响，其分析结果可应用于地震引起的灾害损失评估和抗震加固改造决策，而这一条件概率即为结构易损性。

对于高桩码头的地震易损性研究，已有很多学者开展了研究，但基本上都是国外学者[3-7]开展的研究，国内目前只有冯云芬等[8]开展过相关研究，而且上述研究均针对混凝土桩码头。另外，在码头地震易损性分析中，通常须采用非线性动力时程分析方法对码头有限元模型进行分析，以确定码头在不同地震动强度下的地震反应值，再将反应值与码头结构的不同破坏状态的定义值进行对比，则可得到结构在不同地震动强度水平下发生不同破坏状态的概率，然后将破坏的概率拟合成易损性曲线[8]。由于码头结构的破坏状态一般根据规范确定，因此合理准确地确定码头的地震反应值是易损性分析的关键。在上述研究中，对于码头的时程分析均是直接针对实际结构开展的，由于复杂的桩-土相互作用，且易损性分析须采用大量的地震波以考虑地震动的不确定性，故使得易损性分析的计算量非常大，不便于工程应用。目前，在工程结构的非线性时程分析中，为降低计算的复杂性，将原结构简化为单自由度体系已是一种通行的做法，针对不同结构形式，已有学者提出了多种单自由度模型[9-11]，但尚未对钢管桩码头易损性分析开展相关研究。

建立等效单自由度模型的关键是确立合理的恢复力模型，本文基于光滑型骨架曲线和Masing准则建立钢管桩码头的恢复力模型，其中骨架曲线可由码头的推覆分析确定；为验证本文提出的单自由度模型在码头地震易损性分析中的合理性和有效性，对一个钢管桩码头案例进行易损性分析，比较原型结构和单自由度模型的易损性曲线的差异。

1 单自由度模型的构建

考虑到钢管桩是钢构件，而钢构件本身并不具有负刚度特性，但由于P-Δ效应的影响，其骨架曲线也可能出现负刚度现象。考虑到码头的水平承载力主要由陆侧桩提供(陆侧桩的自由长度小)，通常可忽略P-Δ效应的影响，故本文不考虑骨架曲线的负刚度现象。结合文献[10]和[12]对钢管桩码头恢复力特性进行研究，本文采用式(1)描述的曲线型骨架线，见图1。

(1)

式中：F为钢管桩码头水平承载力；Δ为水平位移；Δ1和F1分别为首个桩塑性铰形成时的上部结构水平位移和水平力；α和β为参数，可按表1确定。文献[12]在确定α和β时考虑了桩-土相互作用。对于Δ1和F1，可通过对码头进行推覆分析予以确定。对于滞回规则，同样参考文献[10]和[12]，采用Masing准则。

注：Δm为最大水平位移；Fm为最大水平位移对应的水平力。

图1恢复力模型

表1 参数α和β的值

注:Su为黏土的不排水抗剪强度，对Su的中间值可通过线性插值予以确定α和β。

在确定好单自由度模型的恢复力模型后，对于单自由度模型的质量m，可以按照式(2)计算：

m=KT2/(4π2)

(2)

式中：K为码头弹性刚度，可取为码头Pushover曲线的原点到首个桩塑性铰形成点连线的斜率；T为码头的自振周期，可对实际码头进行振型分析后确定，取为振型参与系数最大(码头横向反应)的振型对应的周期。对于单自由度模型的阻尼比，一般参考规范[13]，取为5%。

2 易损性分析

参考文献[8]，选用位移作为衡量码头抗震性能的指标，相应的易损性函数可用下式表示：

(3)

式中：C和D分别为钢管桩码头的位移能力和位移需求；IM为地震动的强度参数；Φ(·)为标准正态分布函数；μD为钢管桩码头在不同破坏极限状态下的位移能力均值；μD为码头在相应的IM下的位移需求均值；βC和βD分别为码头位移能力和位移需求的对数标准差。另外，当位移能力μC是由Pushover分析确定时，βC的值可为0.3。

在确定码头易损性函数的方法中，云图法的计算量较小，故本文考虑采用该方法确定码头易损性函数。采用云图法确定码头位移需求的概率模型时，假定位移需求的概率分布为对数正态，且D和IM之间满足以下的指数关系：

D(IM)=a(IM)bε

(4)

式中：a和b为参数，可通过回归分析计算；ε为均值是1的对数正态随机变量，同时其对数标准差为βD。对式(4)的等号两侧分别取对数可得：

我早已设计好，这次一定要双手捧花，单膝跪地，绅士般求婚，“嫁给我吧。”然后拥抱，热烈的吻，吻个死去活来。

ln[D(IM)]=lna+bln(IM)+lnε

(5)

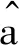
(6)

(7)

式中：Di为第i次非线性时程分析得到的钢管桩码头位移需求；n为计算中采用的地震波数目。由此，利用式(6)和(7)确定μD和βD后，将数值代入式(3)，则可得到钢管桩码头的易损性函数。

对于钢管桩码头的破坏极限状态，本文考虑文献[14]定义3个破坏状态，分别为破坏状态I-最小破坏、II-可控且可修复的破坏和III-可保障生命安全的破坏，并用钢管桩的塑性铰材料应变εs表示，见表2，其中地基深处桩塑性铰是指塑性铰所在位置的深度大于10倍桩径。

表2 钢管桩码头破坏状态

3 案例分析

3.1 案例概述

钢管桩码头断面见图2，排架间距为6.3 m，码头分段长度为47.1 m。钢管桩直径为800 mm，壁厚是10 mm，钢材为Q345。岸坡土体为单一的砂土，其内摩擦角为30°。

图2 钢管桩码头断面(高程：m；尺寸：mm)

3.2 地震波

地震波从美国太平洋地震工程研究中心的强震数据库中选取，共50条。限于篇幅，地震波的相关信息从略。

3.3 易损性分析结果

采用SAP2000建立码头有限元数值分析模型，相关建模方法可参考文献[12]。首先进行码头推覆分析，可得码头的荷载-变形曲线(Pushover曲线)，见图3，图中给出了首个钢管桩塑性铰出现时对应的位置，并给出了不同破坏状态对应的位置。不同破坏状态I、II和III下的μC分别为8.7、13.2、17.4 cm。

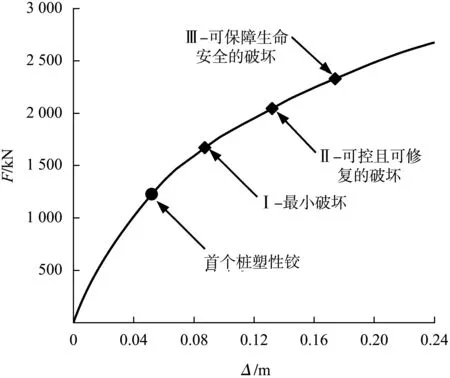
图3 Pushover曲线

利用推覆分析得到的首个桩塑性铰形成时的码头水平位移Δ1和水平力F1，可由式(1)确定等效单自由度模型的骨架曲线，再结合Masing准则和式(2)即可建立码头的单自由度模型。采用云图法确定码头易损性时需要计算每一条地震波下实际码头和单自由度模型的位移需求，但是需要指出的是，本文中的单自由度模型只是用于确定码头的横向位移反应，而计算码头总位移需求则需要考虑码头扭转和双向水平地震动的影响，本文采用文献[14]的动力放大系数DMF来考虑这一影响，即在计算确定的码头横向位移需求的基础上乘以DMF，进而得到码头的总位移需求D。DMF的计算公式如下：

(8)

式中：e0为码头的初始偏心距；Ll是码头分段长度。对于本案例，经计算可得e0=6.40 m、Ll=47.1 m，代入式(8)后可得DMF=1.498。

通过非线性时程分析确定码头的总位移需求后，考虑地震动强度参数IM选用峰值地面加速度PGA，可得位移需求D和PGA之间的关系，见图4，再根据式(6)和式(7)则可确定μD和βD。对于实际码头和对应的单自由度模型，μD可分别由式(9)和(10)计算，βD分别为0.371 5、0.341 5 cm。

lnμD=0.696 8ln(PGA)+3.081 8

(9)

lnμD=0.613 0ln(PGA)+2.992 8

(10)

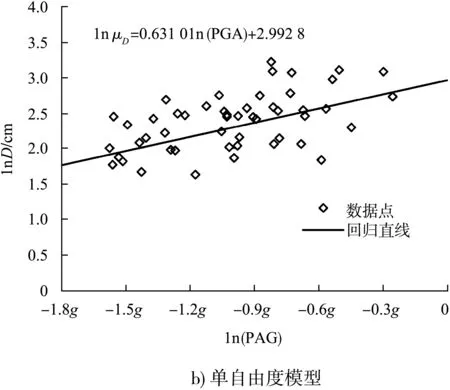
图4 位移需求D的回归分析

图5 易损性曲线

将式(9)和(10)以及计算得到的βD代入式(3)，可得实际码头和单自由度模型的易损性函数，将函数用几何图形表示出来，即可得易损性曲线，见图5。由图5不难看出，随着PGA的增大，码头结构发生破坏的概率逐渐增大，而且发生破坏状态III的概率低于破坏状态I和II，说明码头发生不可修复的破坏的概率较低；总体上实际码头和单自由度模型的易损性曲线相差不大，特别是在破坏状态I的情况下；在峰值地面加速度PGA小于0.5g的情况下，二者的差别很小，但随后二者的差距变大。考虑到二者易损性曲线的差别很小，因此在对实际钢管桩码头进行易损性分析时，可以按本文的方法构建单自由度模型以代替原结构进行分析，以减小计算量和计算难度；另外，考虑到单自由度模型和实际码头易损性曲线在PGA大于0.5g的情况下有一定差别，故在此情况下的单自由度模型计算结果应慎重使用。

4 结论

1) 采用曲线型骨架线和Masing准则构建的单自由度模型可代替实际钢管桩码头进行易损性分析，其易损性曲线与实际码头的曲线存在一定差别，但差别不大。

2) 采用单自由度模型进行钢管桩码头易损性分析可以极大地降低计算量，但仍然无法避免进行大量的非线性时程分析，在下一步研究中可考虑对单自由度模型进行参数分析，研究易损性曲线和相关参数的关系，进而建立标准化的码头易损性曲线供码头抗震评估使用。