边界层对致密油藏逆向渗吸的数值模拟

徐中一，方思冬

(中国石化 石油勘探开发研究院，北京 100083)

目前致密油藏开发过程中的渗吸传质作用十分复杂，其复杂性主要集中在两个方面，第一由于缝网的存在大幅度增加了基质-水的接触面积，导致渗吸的范围增加；第二因为致密储层的喉道细小达到了微纳米级别[1-4]，已经达到了流体分子尺度的级别，因此微纳米喉道内的微尺度效应将十分明显，在微尺度效应的影响下普通油藏适用的达西定律在致密油藏中可能不再适用。

为了准确模拟致密储层渗吸流动，本文首先基于耗散粒子动力学(DPD)方法在微纳米喉道中模拟了油水两相的渗吸流动过程并证明了微纳米喉道中存在边界层效应，通过调研现有的文献以及DPD模拟结果综合表征了边界层厚度的变化规律，在此基础上利用孔隙网络模型计算致密储层的有效渗透率、相渗曲线及毛管力曲线；同时，利用已有的渗吸速度计算模型结合得到的关键渗流参数，得到关于致密储层的渗吸速度的变化规律，将实验结果与计算结果对比验证本文提出的关键渗流参数的计算方法是否正确，最后，利用数值模拟方法阐明致密储层中考虑边界层的渗吸对开发效果的影响。

1 致密储层的微观流动

1.1 渗吸过程中边界层现象两相的情况

采用耗散粒子动力学(DPD)方法对纳米喉道内的渗吸现象进行了模拟，整个模型由3种珠子构成，油珠子、水珠子和二氧化硅珠子，其中二氧化硅珠子用作构建石英微圆管，二氧化硅分子被分为两类，第一类SiO2珠子用于构建石英微圆管内部，第二类SiO2珠子用于构建石英微圆管的管壁，两种SiO2粒子的受力不同，第一类石英微圆管内部的SiO2珠子受力主要是SiO2珠子间的结构力，第二类石英管表面的SiO2除了与第一类SiO2珠子间存在结构力外还有与流体间存在相互作用力，微圆管内壁表面的SiO2作为非极性分子与水中的氢离子结合形成羟基，带有羟基的SiO2珠子与H2O珠子之间会形成氢键，导致了壁面对水的吸引[5]。将二氧化硅珠子均匀排列构建微圆管并作为流体的流动通道，油珠子和水珠子分别构成了渗吸过程中的油水两相，粒子的基本参数如表1所示，在表1中的amu为原子质量单位，它的定义为碳12元素原子质量的1/12;Å为半径的长度单位埃，Å比纳米小一个数量级，1埃等于0.1nm。

接下来只要准确构建粒子间相互作用力就可以准确模拟微纳米喉道中的渗吸流动，根据DPD理论珠子间的相互作用力主要有3种[6-7]：保守力、耗散力和随机力，其中耗散力的设置依据田虓丰博士论文的设置，耗散力半径为1.5(12Å)时，耗散力系数为45(0.885 42 amu/fs)时，密度为3(1g/cm3)的流体粘度为1 mPa·s[7]。此时当体系内有油相后，粒子的密度为5(1.6 g/cm3)时[7]，将粒子的截断半径调大，设置为20Å时，此时流体粘度的粘度增加为3 mPa·s。而随机力和耗散力有直接的关系，当耗散力确定后，软件会根据耗散力的设置自动设置随机力[5]，保守力参数的计算根据Flory-Huggins理论,分子间的保守力计算如式(1)和式(2)[8-9]：

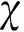
(1)

其中χ为Flory-Huggins相互作用参数，Flory-Huggins的相互作用参数一般通过式(2)得到[11]：

(2)

式中：χ为Flory-Huggins相互作用参数，J/(mol·K)；V为粒子平均摩尔体积，cm3/mol；R为气体常数，8.314 J/(mol·K)；T为温度,K;δA,δB为粒子的溶解度参数，(J/cm3)0.5。

利用Material Studio(MS) 软件中的Forcite模块计算溶解度参数，将计算获得的溶解度参数输入MS软件的DPD模块获得最终的各珠子间的保守力系数如表2所示。

另外为了准确的描述管壁亲水作用，需要在普通耗散粒子动力学方法的基础上添加管壁SiO2珠子和水珠子间额外的吸引力，根据实验室测得的边界层厚度变化规律以及极限边界层厚度[12]，选用MS软件所提供的纯吸引力函数LJ96X[如式(3)]，且其参数为D0=1，R0=1，E=1时，其拟合得到的边界层厚度的变化规律与实际相符。

(3)

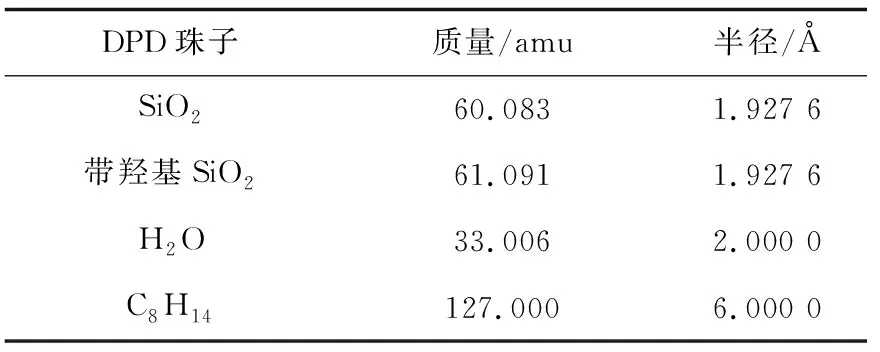
表1 DPD粒子基本参数Table 1 Basic parameters of DPD particles

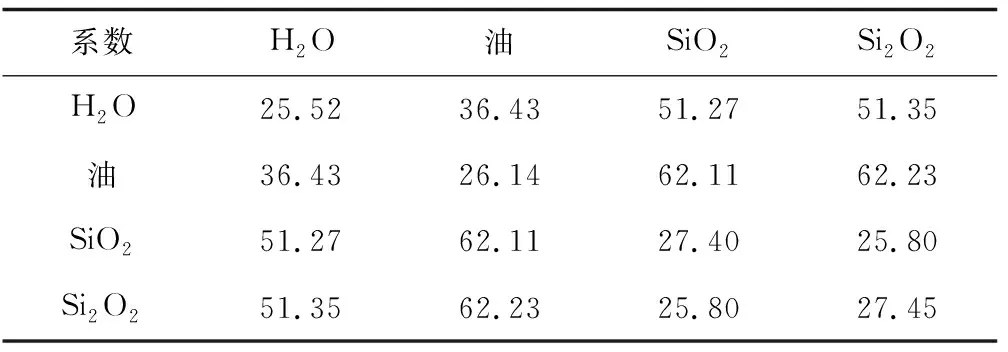
表2 粒子保守力系数Table 2 Particle conservative force coefficients

式中：F为吸引力，N；D0为吸引力参数，kcal/mol；R为粒子间距离，Å；R0为粒子间平衡距离，Å；E为偏移距离，Å。

将表2中计算得到的粒子间作用力参数以及LJ96X吸引力函数输入MS软件中的DPD模块，进行模拟计算，计算结果如图1所示，图1a显示的是渗吸模拟过程中珠子分布图，图1b显示的是水珠子的密度分布图；从图中可以看出，在渗吸阶段水珠子在管壁珠子的吸引力作用下进入微圆管壁，并在管壁处形成了边界层，远离管壁处的水珠子则形成弯液面向管内推进。

1.2 模型的抽提及边界层的定量表征

根据DPD研究显示的边界层现象，抽提得到致密储层渗吸时的模型(图2)，模型显示当考虑致密多孔介质喉道为4～200 nm时，边界层现象都十分明显。根据邹才能对致密储集层特征的描述，致密油储集层孔喉直径主要分布在50～800 nm,孔隙度小于10%，渗透率为1×10-6～1×10-3μm2 [10]。根据上述研究，在致密储层微纳米喉道中，不能忽视边界的存在；边界层对致密储层中渗吸过程的影响如图2所示，微纳米喉道中的边界层会减小有效流动空间，如图2b所示rori为致密储层多孔介质的原始喉道半径，边界层被认为是静止的不参与喉道内流体的流动，原始喉道半径减去边界层厚度h后则为喉道内流体的有效流动半径reff，相比于中低渗油藏，致密储层由于本身喉道细小加上边界层的作用导致有效流动半径的进一步减小。

为了定量表征边界层对流动的影响，根据本文DPD模拟结果以及李洋等人实验结果[12]，边界层厚度可以定量表征为公式(4)，公式(4)具有一定的适用范围，应用时喉道壁面需完全润湿，压力梯度不得小于0.02 MPa/m，同时喉道半径需小于0.2 μm，管内的流体需是牛顿流体[9]。

(4)

式中：r为孔隙的喉道半径,μm；h为孔隙中的边界层厚度,μm；μ为流体粘度,mPa·s；Δp为压力梯度，MPa/m。

2 致密储层关键参数的计算

根据徐中一关于渗吸的文章,准确计算渗吸量需要准确计算渗透率、油水相渗、毛管力曲线3个关键渗流参数[9]，本文使用孔隙网络模型，在流动模拟的过程中考虑边界层对流动的影响，直接计算以上3个关键渗流参数。

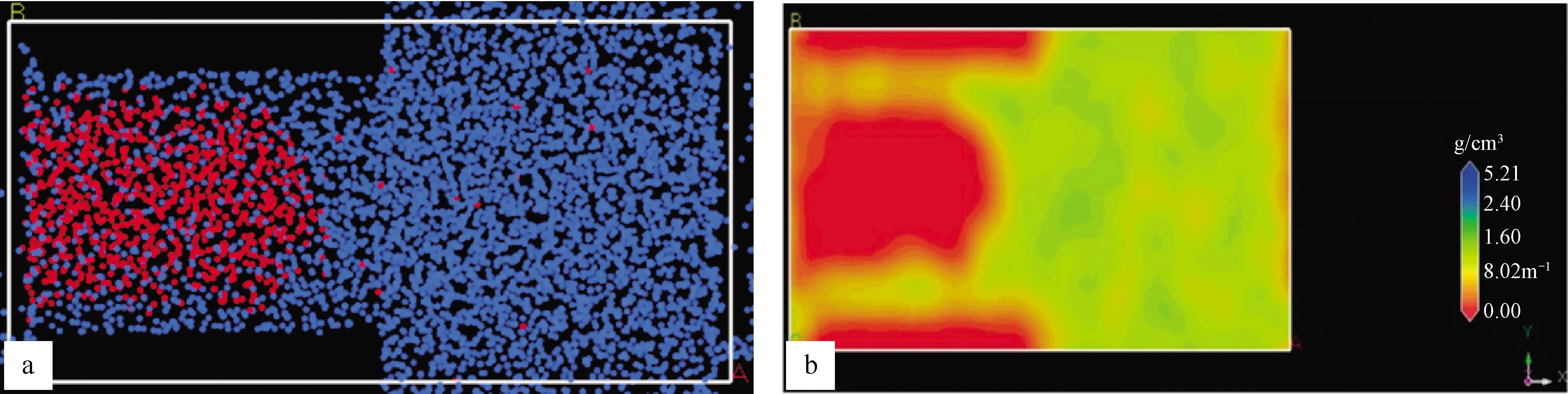
图1 耗散粒子动力学(DPD)模拟结果Fig.1 Diagram of Dissipative Particle Dynamics (DPD) simulationa.粒子图；b.流体密度图

图2 基于DPD实验建立的考虑边界层的两相流动模型Fig.2 A two-phase flow model considering boundary layers based on DPD experimentsa.不考虑边界层时的渗吸情况；b.考虑边界层的渗吸情况

2.1 渗透率的计算

依据核磁公振实验对实际致密岩心在饱和水状态下测得的T2谱经过转化后获得的实际致密多孔介质中孔隙大小的分布，如图3a所示，将致密储层的多孔介质处理为三维的随机网络模型，将多孔介质中较大的空间简化为球型孔隙，较小的空间简化为圆柱状喉道，节点代表孔隙在三维空间的位置，节点间的连线代表孔隙间的喉道，其中无论是孔隙和喉道都要满足致密储层多孔介质内孔隙和喉道的分布，最后形成的孔隙网络模型如图3所示。孔隙和喉道大小都满足截断高斯韦布尔分布[公式(5)][13-15]，通过调节参数rmax、rmin使得孔隙网络模型中的孔隙分布范围与图3a实测的孔隙分布范围相符。

r=(rmax-rmin)(-δln[x(1-e-1/δ)+e1/δ])1/γ+rmin

(5)

式中：r为喉道半径，μm；rmax为最大喉道半径，μm；rmin为最小喉道半径，μm；γ、δ为几何分布参数，无因次；γ=-1，δ=-1使得喉道和孔隙规则分布；x为随机变量，取值范围0～1。

计算渗透率时，首先在孔隙网络两侧，流体的入口和流体的出口分别设置恒定的压力，使得孔隙网络中的流体在恒定的压力梯度下流动，孔隙网络模型内部的情况如图4a所示，孔隙间喉道中的流体在流动的过程中存在着边界层，边界层的厚度根据式(4)计算；在计算过程中首先计算每个孔隙处的压力，依据每个喉道相连的孔隙的压力与喉道本身的长度计算喉道内的压力梯度，从而计算每个喉道内的边界层的厚度，因为边界层是不参与流动的所以边界层的存在就减小了喉道内流体的有效流动空间。最后在孔隙网络模型两端(如图4a所示的入口和出口)设置不同的压差,每设置一个压差就计量孔隙网络模型末端的流量，最后用公式(6)计算致密储层的渗透率。

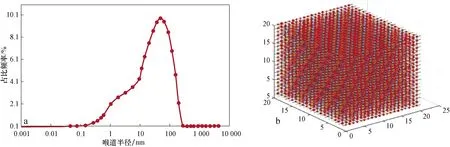
图3 构建的孔隙网络模型Fig.3 Pore network modela.孔隙大小分布；b.依据孔喉分布建立的20*20*20的孔隙网络模型

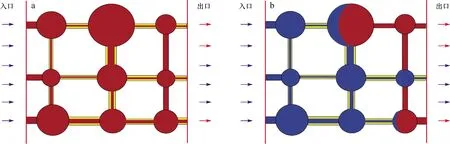
图4 二维孔隙网络模型中驱替和渗吸的情况Fig.4 Schemes showing displacement and imbibition in a two-dimension pore network modela.驱替的情况；b.渗吸的情况

(6)

式中：k为渗透率，10-3μm2；q为出口端的流量，cm3/s；μ为流体的粘度，mPa·s；L为孔隙网络模型的长度，cm；Δp为孔隙网络两侧的压力差，MPa。

通过以上方法计算出的渗透率如图5所示，可以看出当不考虑边界层的多孔介质而言，渗透率是一个仅与多孔介质有关的参数，只要多孔介质一定无论怎样改变压力梯度，渗透率的大小都不变；考虑边界层后渗透率就不仅与多孔介质本身有关而是与流体流动有关，从图5可以看出当压差较小时，边界层厚度较大，有效流动空间较小，因此有效渗透率偏离不考虑边界层时的渗透率，而随着压力梯度的增大，边界层厚度逐渐减小，直到压力梯度很大达到104MPa/m时，边界层厚度远小于喉道半径，此时边界层的可以忽略。因此随着压力梯度的增大，致密多孔介质的渗透率逐渐接近不考虑边界层的多孔介质的渗透率。

2.2 相对渗透率与毛管力曲线的计算

渗吸的过程是一个两相流动的过程，因此需要计算致密多孔介质渗吸过程的油水两相相渗曲线和毛管力曲线，本文同样采用孔隙网络模型，基于Blunt公布的流动模拟程序[16]，在其程序的基础上增加了边界层计算模块，核心的计算步骤如图6所示，主要需要计算每个孔隙处的压力值，然后根据压力值和喉道的长度计算每个喉道的压力梯度再根据压力梯度计算每个喉道的边界层厚度，值得注意的是，如图4b所示只有水湿的喉道需要计算边界厚度，油湿的喉道是不存在边界层的；计算完边界层后再计算由于边界层的变化导致的喉道的传导系数的变化。

渗吸的过程不同于计算渗透率的驱替过程，是在入口和出口设定恒定的压力；渗吸的边界条件是在入口设置恒定的含水饱和度为1，出口端设置恒定的压力，本文设置了大气压力0.101 MPa，初始时刻每个孔隙处的压力也是大气压力，计算得到的相渗曲线和毛管力曲线如图7和图8所示。

计算结果表明边界层对于致密储层的相对渗透率曲线和毛管力曲线有较大的影响，从计算得到的相渗曲线图7a来看，边界层的存在主要减弱了油水两相在多孔介质中的流动能力，同时边界层的存在会使得油水两相区缩小，束缚水饱和度和残余油饱和度都增加，这是因为边界层的存在使得越来越多的油被“锁”在基质中无法通过渗吸作用流出多孔介质。

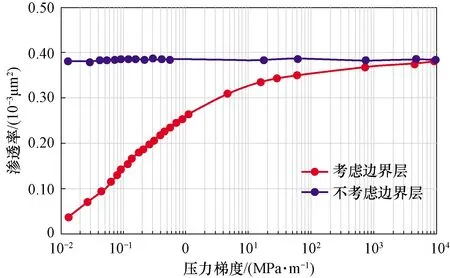
图5 考虑边界层后渗透率的变化Fig.5 A plot showing the permeability variation before and after considering boundary layers

图6 技术路线Fig.6 The workflow in technology

从毛管力曲线图7b来看，考虑边界层后其毛管力曲线大小明显较不考虑边界层的情况要大，这主要是边界层的存在减小了喉道的有效流动空间，根据公式pc=2δcosθ/r可知当有效流动半径减小时，毛管力会增大；同时毛管力开始发生上翘的点发生了右移，这说明很多原先润湿相可以进入的喉道和孔隙现在因为边界层的存在现在无法进入，因此总的来说毛管力的存在导致毛管力大小增加，另外可流动的喉道和孔隙数减少。

3 考虑边界层情况下传质计算及验证

为了验证以上计算结果的正确性，本文挑选了致密岩心进行了自发逆向渗吸实验，并将实验测得的渗吸采收率曲线与计算得到的渗吸采收率进行对比，实验首先将岩心在真空泵中抽真空后饱和配置的重水，然后放入核磁共振仪中测量T2谱，并利用油驱水实验制造束缚水，最后取出岩心并除去岩心表面的浮油，最后把岩心放入盛满水的烧杯中进行渗吸实验(图8)，实验过程采用称重法对渗吸出的油量进行称重，渗吸实验共持续6d左右达到最终采收率，实验的岩心的基本参数列于表3中。

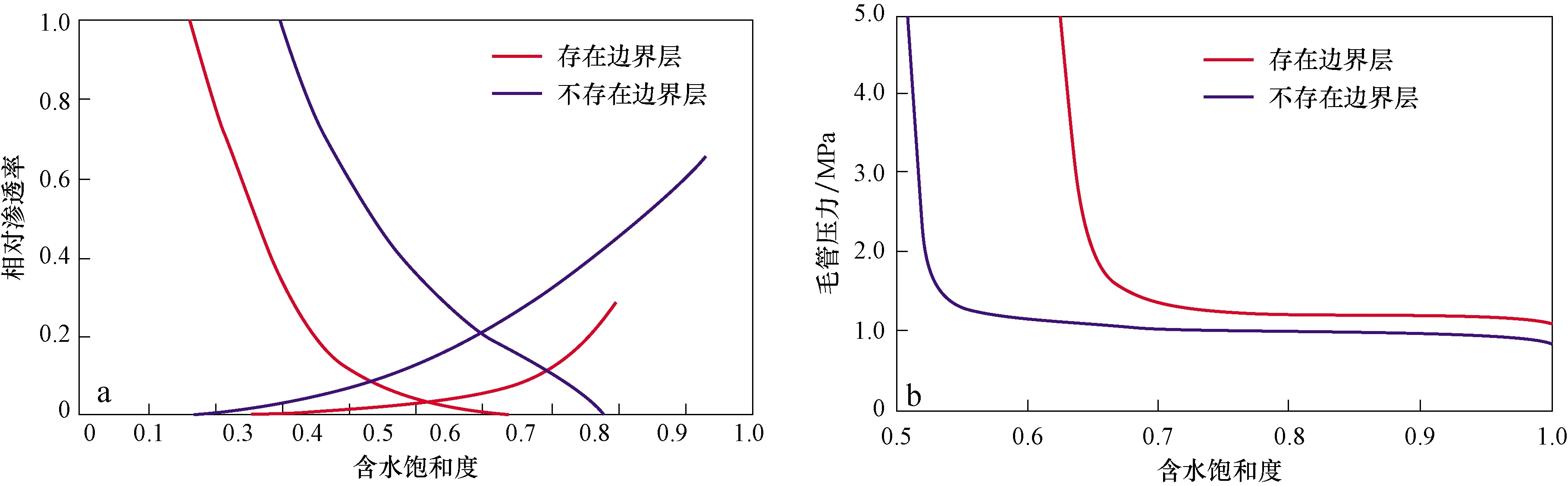
图7 渗流参数计算结果Fig.7 Calculated results of seepage parametersa.相对渗透率曲线;b.毛管力曲线

本文第二节的孔隙网络模型的孔喉分布是基于本次核磁公振测得的T2谱转化获得的，另外第二节计算的渗透率、相对渗透率、毛管力曲线就是基于本次实验的岩心测得的孔喉分布建立的孔隙网络模型计算的，将计算得到的渗透率曲线、相对渗透率曲线、毛管力曲线综合起来利用RIBEM方法[17]计算渗吸量，结果如图9所示，考虑边界层后渗吸速度和渗吸的最终采收率都大幅降低，当不考虑边界层时计算得到的采收率为18%，达到最终采收率所需的时间为40 h，而考虑边界层时最终采收率仅为10%，达到最终采收率所需的时间为6 d左右，说明致密岩心的渗吸速度远小于不考虑边界层的情况。

4 油藏尺度数值模拟计算

最后为了研究在油藏尺度下渗吸对致密油藏开发效果的影响，本文采用非结构PEBI网格贴合人工水力压裂缝对致密储层中水平井周围的缝网进行网格剖分如图10所示，图中人工裂缝显式描述，诱导缝和天然裂缝采用双重介质模型描述[18-23],将本文第二节计算得到的渗流参数应用到当前的油水两相数值模拟计算中，通过对比不同时刻油藏的含水饱和度和产量，评价边界层对致密储层开发效果的影响。

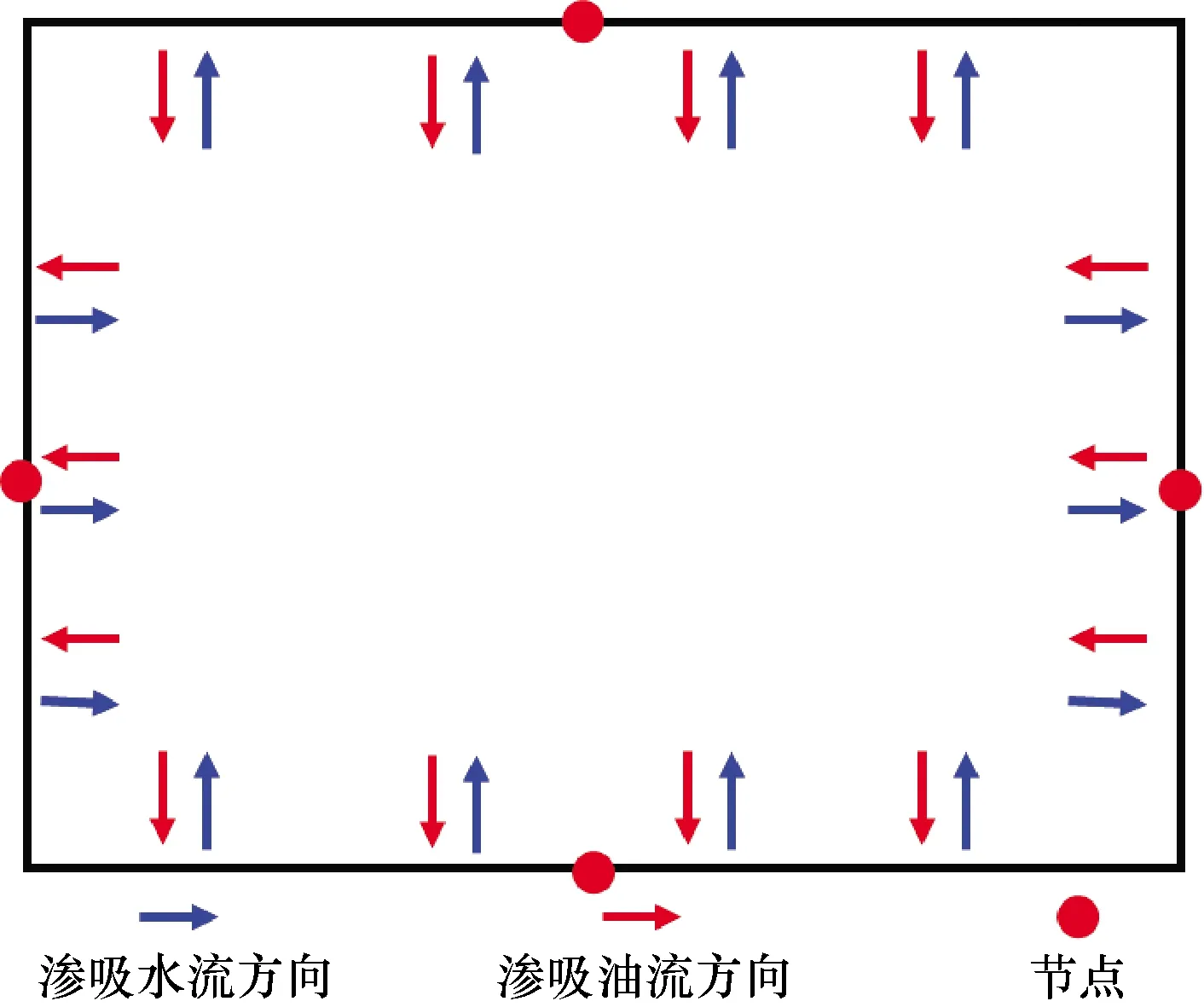
图8 渗吸实验岩心示意图Fig.8 The schematic diagram showing the core imbibition experiments

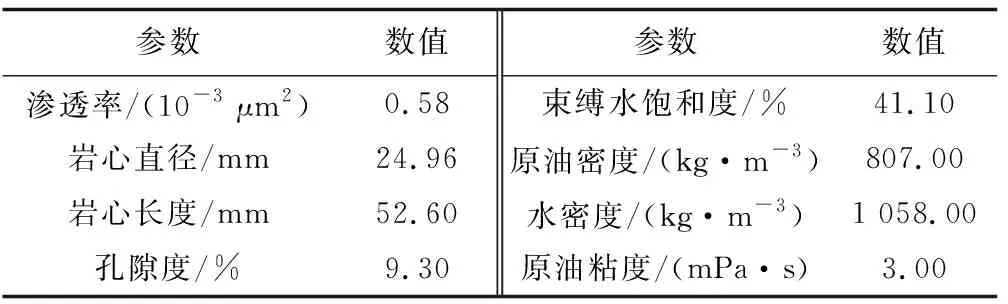
表3 岩心基本参数Table 3 Basic parameters of core

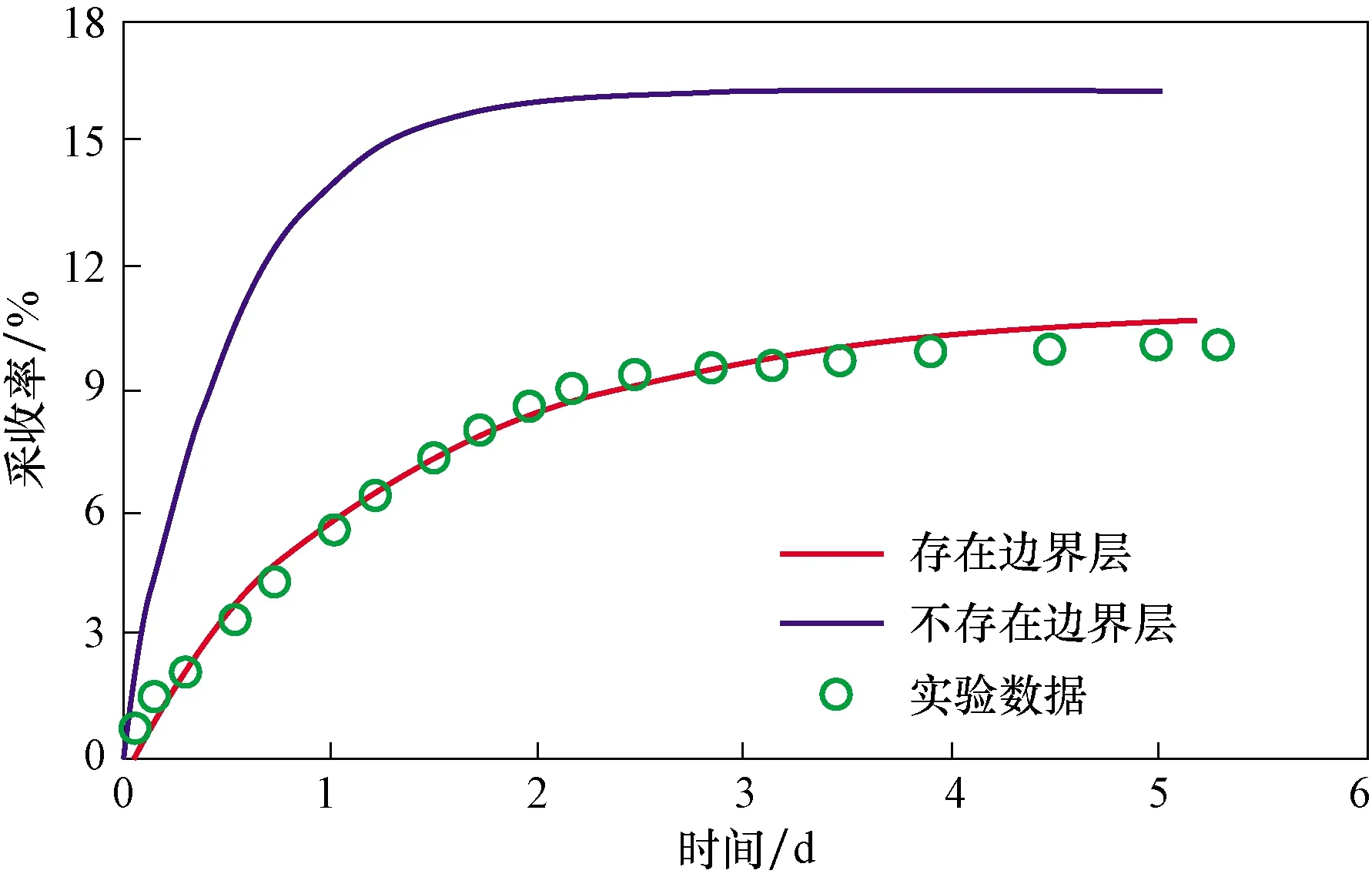
图9 计算渗吸采收率与实验结果对比Fig.9 The comparison between the calculated and measured imbibition recovery

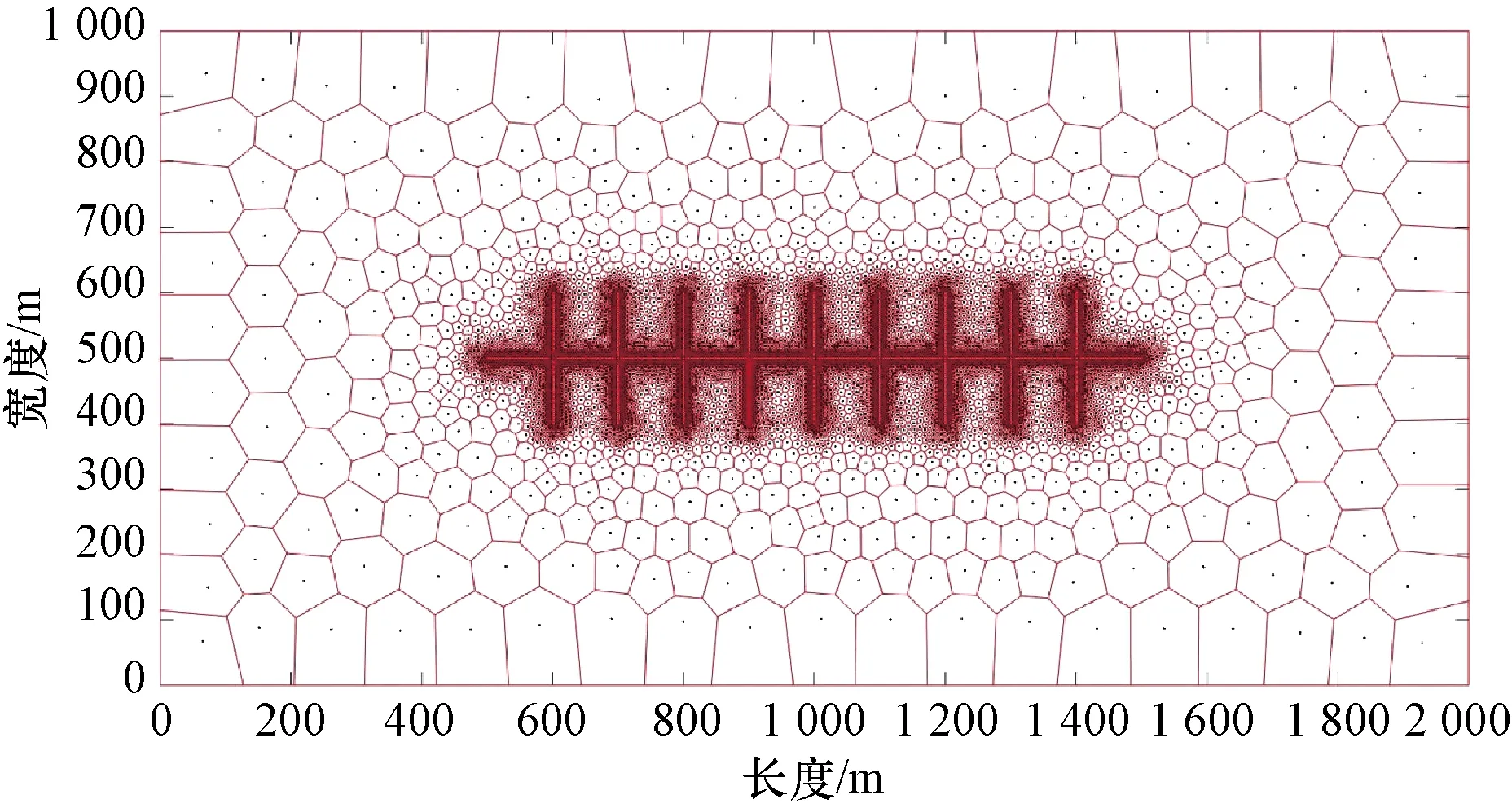
图10 考虑缝网的PEBI网格模型Fig.10 A PEBI fracture network model

本部分模拟了水平井的注水吞吐开采，吞吐一共持续五个轮次，每个轮次持续50 d，每个轮次内前10 d注水，焖井20 d，后20 d开井生产。与模拟有关的参数如表4所示，第一轮次、第三轮次及第五轮次的模拟结果如图11及图12所示，图中主要展示了不同轮次焖井末期的含水饱和度分布。其中图11展示了不考虑边界层情况下的含水饱和度分布，图12展示了考虑边界层情况下的含水饱和度分布，油藏的基本参数如表4所示。

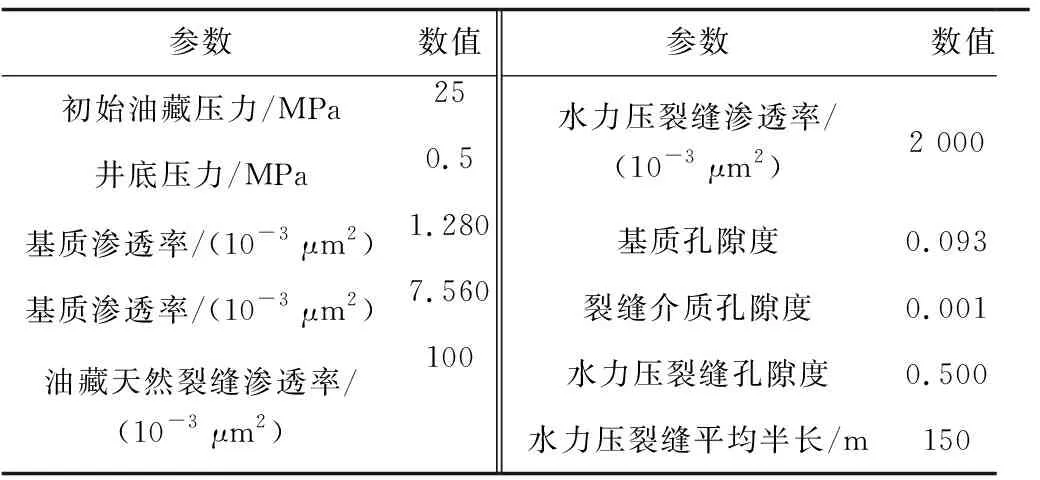
表4 数值模拟基本参数Table 4 Basic parameters of numerical simulation

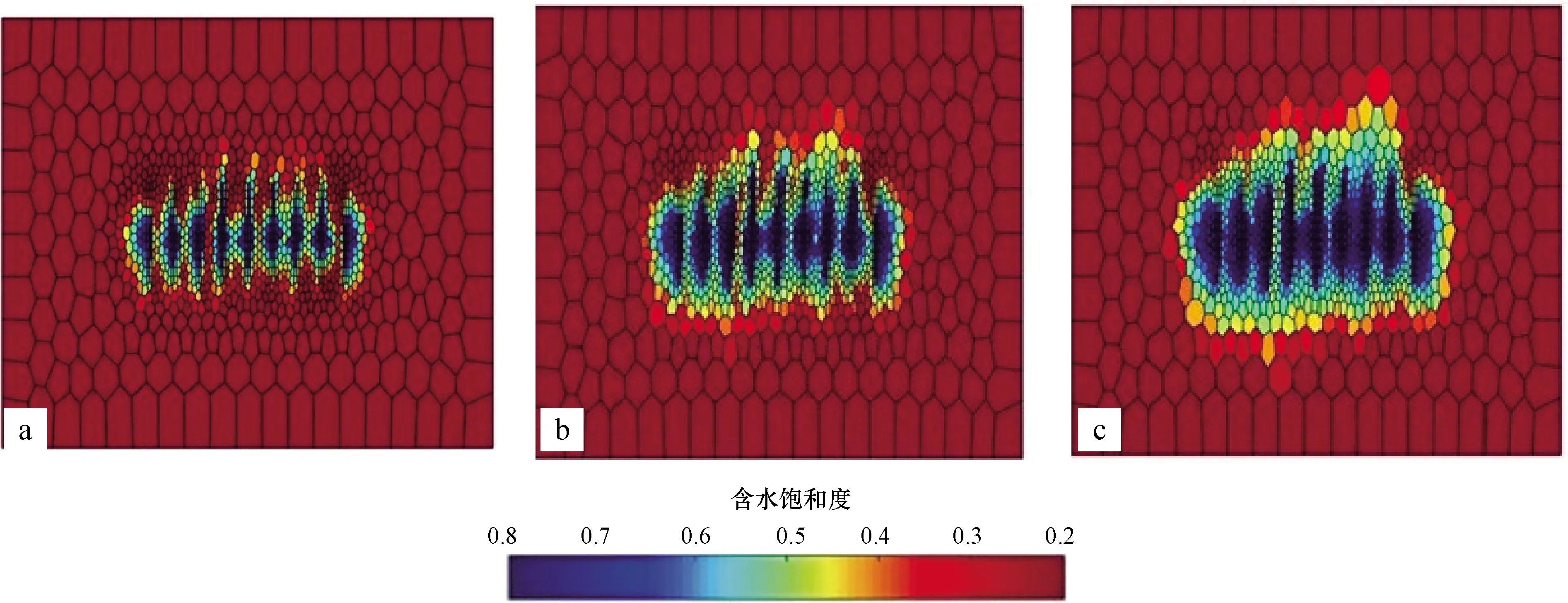
图11 不同轮次致密油藏考虑边界层情况下含水饱和度分布对比Fig.11 The comparison of water saturation variation in tight reservoirs considering boundary layers at different water-injection roundsa.第一轮次；b.第三轮次； c.第五轮次

图12 不同轮次致密油藏不考虑边界层情况下含水饱和度分布对比Fig.12 The comparison of water saturation distribution in tight reservoirs without considering boundary layers at different water-injection roundsa.第一轮次； b.第三轮次； c.第五轮次

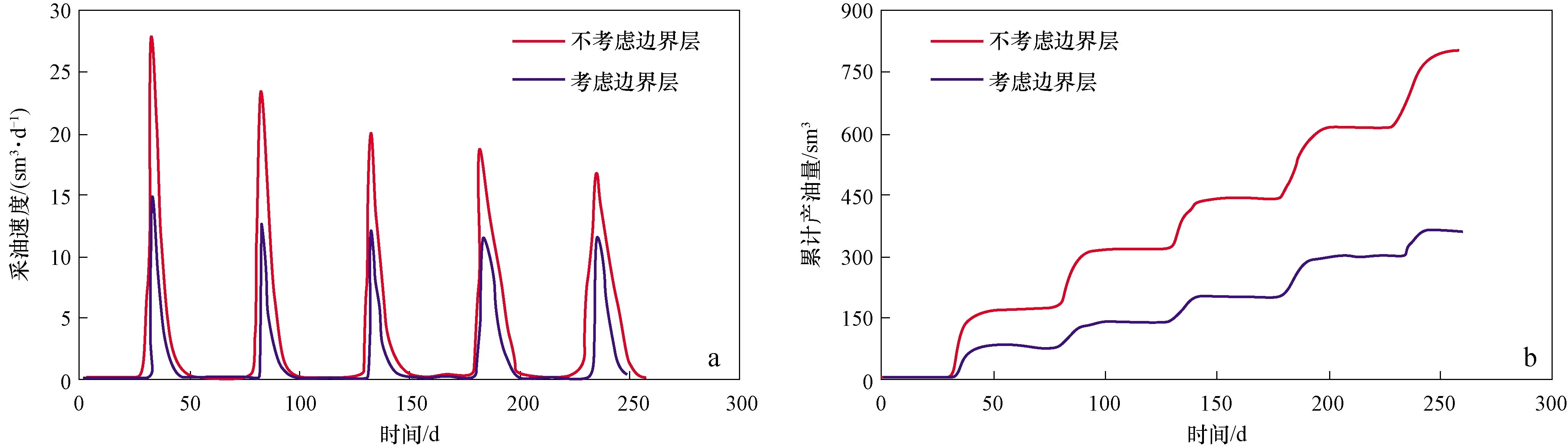
图13 生产情况对比Fig.13 The comparison of oil production with and without considering boundary layersa.采油速度对比;b.累计采油量对比

从数值模拟横向对比的结果来看，将第五轮次与第一轮次和第三轮次进行对比可以看出渗吸的吸水排油作用对压裂水平井周围含水饱和度具有一定影响，当考虑边界层时，由于其渗吸能力较弱(吸水排油的能力弱)，吞吐周期内注入的水更多的滞留在裂缝介质内，导致压裂水平井周围的含水饱和度较高。

从数值模拟横向对比的结果来看，随着轮次的增加，注入水波及的范围逐渐扩大，这意味着原先没有被注入水波及的不发生渗吸的区域，逐渐被注入水波及开始发生渗吸，也就是说，随着注入水波及的区域越来越大，发生渗吸的区域也越来越大；边界层的存在会影响注入水向外波及的速度，考虑边界层时，渗吸能力弱，更多的水滞留在裂缝中，有利于向外波及，因此当考虑边界层时，轮次增加更多的水能够向外波及从而导致能够发生渗吸的区域比不考虑边界层时的区域大。

压裂水平井的采油速度和累积采油量分别如图13a和图13b所示，从图13a的采油速度可以看出，不考虑边界层的致密储层，其采油速度要高于考虑边界层的储层，相应的考虑边界层情况下的累积采油量大约是考虑边界层情况累积采油量的3/8。造成这种现象的主要原因是考虑边界层后，储层的渗吸能力减弱，吸水排油的效果减弱，滞留在有效流动介质中的水多油少，从而导致最终开采过程中采油速度的减小，另外随着轮次的增加，地层能量不断释放，导致每一轮次的采油能力都在衰减，如图13a所示，采油速度在逐轮次的递减。

5 结论

1) 使用耗散粒子动力学方法探索发现了微纳米喉道中油水两相渗吸过程中的边界层现象，并且得到了边界层变化的规律。

2) 使用孔隙网络模型计算了存在边界层情况下的关键渗流参数，从计算结果来看，对致密储层来讲边界层的存在会减小储层的渗透率，边界层对渗透率的减小程度与压力梯度的大小有关，压力梯度越大边界层厚度越小，边界层对渗透率的伤害越小，当压力梯度达到104MPa/m时，边界层的存在几乎不会对储层造成伤害。

3) 从油藏尺度来看，致密储层中存在的边界层会减弱储层的流动能力以及基质块的渗吸能力，如果忽略边界层会过高估计储层的生产能力，实例计算表明，考虑边界层后累计采油量约为不考虑边界层情况的3/8，因此真实致密储层中采用注水吞吐以期利用渗吸作用提高采收率效果应是十分有限的。