沙堡最佳形状持续时间研究
吕佩珏 王浩然 王子淳 北京理工大学
1 . 引言
儿童和艺术家喜欢用沙子建造城堡。不可避免地,海浪的流入加上涨潮会侵蚀沙堡。因此,我们需要构建一个数学模型,以确定用作沙堡基础的最佳3 维几何形状,确定最佳的沙水混合比,在下雨时调整模型,使用其他策略来延长沙堡的使用寿命,撰写一篇描述模型及其结果的文章。
2 . 侵蚀模型
2.1 基本模型
(1)模型的基础
首先,我们分析了波浪对砂堆的冲蚀作用,使每单位时间在所有区域损失的砂的重量为M。根据水力知识,在砾石类型与坡度相同的条件下,水不可避免地会消耗一部分能量来去除沙子,也就是说,水确实在沙子上起作用,这意味着两者是成正比的,下面的公式(1)(2)反映了这种联系。

其中y 是水的密度,h 是水的深度,U 是水的速度,J 是斜率降,q 是流量。
坡度下降对沙子的侵蚀作用不能完全用水流的力量来表示。又经过分析我们可以得到单位时间内单位面积冲走的沙粒重量的公式(3):

因为两个参数的尺寸不完全相等,所以系数c 是尺寸常数。查阅信息后,得出c=0.218。经过进一步分析,不同的水沙比会改变沙堆的密度。如果引入y/y1-y 进行调整,则可以更好地表达水沙比的特性。其中,y 是水的密度,y1 是沙堆的密度。沙堆的密度也将在1200到1600 之间变化。简化值为每立方米1600 千克。使用曼宁公式,当前斜率可以写为:(4)
其中n 是曼宁粗糙度,R 是水力半径。如果流域是宽还是浅,则可用水深h 代替水力半径R。经过审查,曼宁粗糙度与表面光滑度有关。对于具有光滑表面的对象,n 可以取为0.025。
由此,我们得到公式(5),该公式表示单位时间每单位面积流失的沙粒重量:
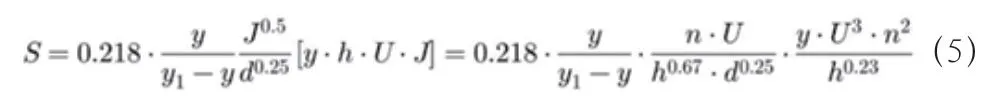
所有物理量均以(kg-ms)单位制。
基于水力学和土壤力学的知识,获得了单位时间每单位面积沙的重量损失,发现在确定土壤力学性能参数的条件下,该函数与水深有着密切的函数关系。为了能够计算出沙堆坍塌所需的时间,我们还需要计算每单位时间与水接触的所有表面上的沙的重量损失。根据开始时的假设,我们可以将沙堆分成N 个相同的三角形金字塔,其中a 是底部三角形的高度,b 是三角形的高度,c 是底部图形的边长。当总砂体积V 固定并定义N 时,a,b 和c 的值将更改。它们之间的关系可以用以下等式表示:

此方程组将在以后用作限定。如果对侵蚀区域进行了积分,则每单位时间与水接触的区域的沙子重量损失A 为A,其中A 是与c 相关的函数。用上面给出的值代替系数为0.838。
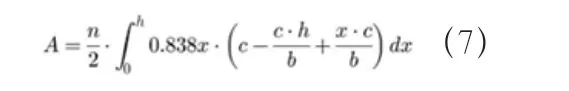
其中x 是代表沿接触面水深变化的变量。
阅读相关文献后,我们发现当沙堆的坡度降至0.2 时,波浪对沙堆的冲刷作用会明显减弱,因此我们假设当b 等于0.2a 时,沙堆的形状就开始了。稳定下来。以下公式可用于计算时间。

获得的时间将是评估沙堆形状的最终依据。
2.2 模型优化
得到模型后,我们需要解决相关参数以获得最佳的沙堡形状。我们需要优化的问题是:在一定体积下获得最佳的边数n 和底部边的长度c。在这里,我们采用总体积V=4,最大波高h=0.1。
蚁群算法:
为了确定函数的参数,我们使用蚁群算法搜索解空间。在自然界中,仅对每只蚂蚁而言,其能力是非常有限的。但是,蚁群可以找到从洞穴到食物的最短路径。
结果:
通过对获得的数据进行分析可以知道,一开始,所有蚂蚁的位置都是完全随机的。但是,当达到迭代次数时,所有蚂蚁都会聚集在极端点。
随着迭代次数的增加,在每次迭代中,最优蚂蚁的极值不断增加,并最终趋于稳定,这证明我们已经找到了最佳参数。在我们的值范围内,当n=25 且c=4.1 时,冲刷时间f 取最大值,即5432。还可以得出当n 接近无穷大时,函数值不断增加。因此,n 的最佳值应该是无限的,即底面形成一个圆。

