多策略自适应变异的差分进化算法及其应用*
胡福年,董倩男
(江苏师范大学电气工程及自动化学院, 江苏 徐州 221000)
1 引言
差分进化DE(Differential Evolution)算法是与遗传算法GA(Genetic Algorithm)[1]、粒子群算法PSO(Particle Swarm Optimization)[2,3]、蚁群算法ACO(Ant Colony Optimization)[4]等相似的一种启发式优化算法,因其简单易实现,可调参数少,具有强大的寻优能力,目前在许多领域的复杂优化问题中得到了应用[5 - 8]。但是,与其它智能算法相同的是,DE算法也存在提早收敛、收敛精度低、搜索停滞等问题。为了提高算法的优化性能,许多学者对此进行了改进,改进方法主要包括以下几个方面:自适应调整控制参数(种群规模NP、缩放因子F和交叉概率因子CR)、设计新的变异算子、变异策略的改进以及混合算法的使用。文献[9]提出了一种自适应DE算法SaDE(Self-adaptive Differential Evolution),通过对之前的方法进行学习逐渐形成选择策略,在算法进化的不同阶段自适应地选择合适的变异策略和控制参数。文献[10]根据解搜索的状态,提出一种自适应种群调整策略APTS(Adaptive Population Tuning Scheme),能够通过排序的方法去除种群中的不良个体,从而达到动态调整种群大小的目的。文献[11]通过对前代个体寻优性能的判断和学习,自适应地对变异策略和参数进行选择,同时加入了具有学习功能的扰动阈值扩大搜索范围。文献[12]提出了一种混合算法,将粒子群优化(PSO)和贪婪随机自适应搜索程序GRASP(Greedy Randomized Adaptive Search Procedure)相结合,增强了算法的搜索性能。以上方法均能在一定程度上提高算法的收敛精度,增强算法跳出局部最优的能力,但在解决一些问题时仍然存在收敛解精度不高、收敛速度慢的现象。
针对上述问题,本文提出一种多策略自适应变异的差分进化MsA-DE(Multi-strategy Adaptive mutation Differential Evolution)算法,根据进化程度随机控制2种变异策略的权重,自适应地选择不同的变异策略,实现算法在解空间的探索与开发能力的平衡。将本文提出的算法与4种常用的改进差分进化算法分别对单峰、多峰等类型的测试函数进行对比分析,结果验证了本文算法的正确性,通过对高速铁路牵引系统功率调节器RPC(Railway Power Conditioner)的容量优化进行仿真分析,验证了该算法的有效性。
2 复杂函数优化问题描述
复杂函数优化问题在经济、计算机科学、工程技术等领域十分常见,从数学的角度来说,对问题的优化就是求解函数极值的过程。采用运筹学的数学规划理论对其进行分析,最小值优化问题可描述如下:
minf(x1,x2,…,xD)

(1)

y′z=[yz+δ-yz-δ]/(2δ),
(2)
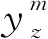
差分进化算法利用了差分的思想,通过群体内个体之间的相互合作与竞争产生的群体智能来指导最优解的搜寻方向,通过不断地进化,保留优良个体,淘汰劣质个体,引导搜索向最优解逼近。下面给出与DE算法优化过程相关的一些定义:
定义1(加权系数法) 为强调某一要素在整个要素体系中的重要程度而赋予该要素某一特征值的过程,特征值即为这一要素的加权系数。
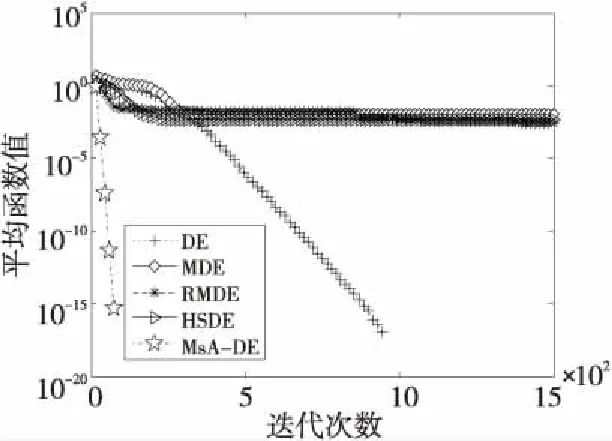
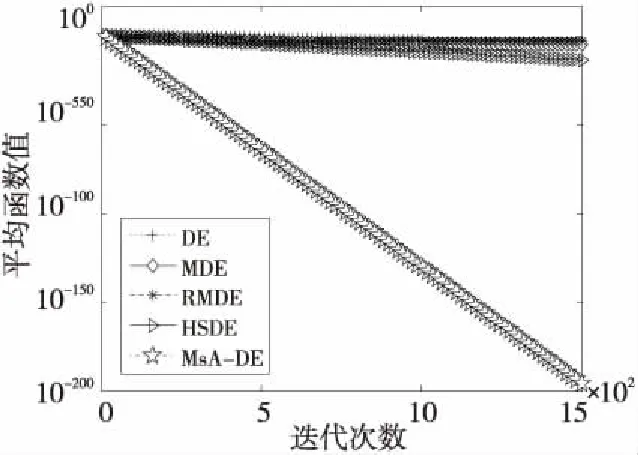
定义2(优劣性) 对于任意2个个体xr1,xr2,若∀j∈{1,2,…,D},(xr1j≤xr2j)∧(∃j,xr1j 针对DE算法在优化复杂问题时易过早陷入局部最优、收敛速度较慢等缺点,对变异策略进行改进。通过分析现有的典型变异算子的优点及不足,提出多策略自适应变异MsA(Multi-strategy Adaptive mutation)算子,同时将随机法和中值法结合,对越界的变异个体进行处理。 3.1.1 经典变异策略 变异操作是DE算法的关键部分,对于算法的优化性能起着重要的作用。在算法进化初期,应当使算法在解空间进行充分的搜索以保证种群多样性;而在算法进化后期,应当将重心从全局最优转移到提升收敛速度上来。为了保证种群的多样性,平衡算法的全局搜索和局部搜索能力,选取3种常用的变异操作结合,以适应算法在不同的搜索阶段中的探索和开发能力的差异。在DE中常用的变异策略为DE/rand/1、DE/best/1、DE/current-to-rand/1、DE/current-to-best/1等。具体形式如式(3)~式(6)所示: DE/rand/1: vi,G+1=xi,G+F·(xr1,G-xr2,G) (3) DE/best/1: vi,G+1=xbest,G+F·(xr1,G-xr2,G) (4) DE/current-to-rand/1: vi,G+1=xi,G+F·(xr1,G-xi,G)+ F·(xr2,G-xr3,G) (5) DE/current-to-best/1: vi,G+1=xi,G+F·(xbest,G-xi,G)+ F·(xr1,G-xr2,G) (6) 其中,xi,G表示第G代的xi,vi,G+1表示第G次迭代后变异产生的个体。F为缩放因子。 3.1.2 新变异策略 由于全局寻优和局部寻优是对立的,因而单一的变异算子很难同时满足2种功能。本文借鉴前人的研究,提出MsA算子,引入动态权重因子ω,将选出的算子集合中不同的2种变异策略进行组合,形成2种新的算子,同时定义1个表示进化程度的值τ,能够在不同的进化时期选择不同的变异策略,表达式如式(7)所示: (7) 其中,τ=G/Gmax,表示当前进化程度,Gmax为总进化代数,ω的产生方法如式(8)所示: ω=ωmin+(ωmax-ωmin)·G/Gmax (8) MsA算子采用算术交叉方式,将当前个体、最优个体和随机个体进行组合,全局最优个体为种群进化提供方向,随机个体则防止种群陷入局部最优,增加种群多样性。MsA算子变异具体过程如下所示: (1)当τ<0.5时,算法进化处于前期,此时变异策略为式(7i),当前个体与随机个体交流,改善了种群多样性,增强了全局搜索能力。 (2)当τ≥0.5时,算法进化处于中后期,此时变异策略为(7ii),当前个体和最优个体与随机个体进行算术交叉,产生变异个体,有利于提高收敛速度和解的精度。 考虑到变异后可能会有个体跳出事先设定的空间范围,此时需要对个体的越界情况进行处理,当个体发生越界时,在对应的目标个体和对应边界值之间随机取值,同时考虑一定概率的边界值。具体处理流程如下所示: ifrand<0.5 else else ifrand<0.5 else endif 在经历过变异交叉等操作后,当前解正在向最优解靠近。但是,最优解可能是全局最优,也可能是局部最优。若是全局最优,在选择操作中不会被过滤掉,若是局部最优,则会使种群陷入局部最优而提早收敛。为避免这种现象的发生,本文所提MsA-DE算法加入了2种扰动操作:小概率扰动和柯西扰动。 Figure 1 Comparison map of probability distribution图1 概率分布对比图 柯西分布是一个连续型分布函数,其重要特性之一就是期望和方差均不存在。柯西分布服从X~Cauchy(μ,λ),μ和λ是局部参数,μ=0,λ=1时为标准柯西分布。标准正态分布服从X~N(0,1),取μ=0,λ=1。标准柯西分布与标准正态分布的概率分布对比如图1所示。 可以看出,2种图形均似钟型,相比于正态分布,柯西分布的曲线降落至0的速度慢很多,减小了取值为0的概率,扩大了寻优范围。使用柯西分布产生的随机数扰动最优个体的方法,可避免算法陷入局部最优。柯西随机数分布服从Cauchyi~randci(μ,λ),Cauchyi为个体i对应的柯西随机数,randci为个体i对应的柯西分布函数局部参数,分别取μ=0,λ=0.01。 为进一步增强算法跳出局部最优的能力,加入小概率扰动[13]。为有效结合自适应变异策略和扰动策略,设置1个调和参数Mr,随机选择变异操作和扰动策略。Mr一般取大于0.9的值,流程如下所示: ifrand τ=G/Gmax; ifτ<0.5 vij,G+1=xij,G+ωF·(xr1j,G-xr2j,G)+(1-ω)F·(xr3j,G-xr4j,G) else vij,G+1=ω[xbestj,G+F·(xr1j,G-xr2j,G)]+(1-ω)[xij,G+F·(xbestj,G-xij,G)] else endif 控制参数的改进主要是针对F、CR,它们的取值对于算法能否平衡全局寻优和局部寻优的能力有着至关重要的意义,通常取固定值,但是这样难以适应算法进化的全过程。本文根据个体最优信息和进化程度对F、CR进行自适应调整,将实验个体和父代个体进行比较,若个体进化成功,则参数继承上一代的值;否则,参数将在0~1内重新产生。 3.3.1 自适应变异因子 对于F,在进化的前期应当尽可能地大,这样可以增加搜索空间,快速向全局最优解靠拢,避免陷入局部最优;在进化后期,种群聚集在全局最优解附近,因而需要F值尽可能地小,以提高搜索精度,找到全局最优解。F的自适应调整如式(9)所示,初代种群的进化参数采用式(10)产生。 Fi,G+1= (9) (10) 其中,Fi,1表示第1代、第i个个体的缩放因子;Fi,G表示第G代、第i个个体的缩放因子;Fi,G+1表示第G+1代、第i个个体的缩放因子;Fmin、Fmax分别表示缩放因子的最小值和最大值。ui,G+1为实验个体,是由第G+1代的变异个体vi,G+1与第G代父代个体xi,G生成的。当上一代个体保留下来时,说明上一代的缩放因子较好,此时仍采用上一代的F值,如式(9i);否则,进一步判断算法是否处于进化前期,若是,则F由式(9ii)产生,随着迭代次数的增加F变大,在算法进化前期扩大寻优范围;否则,使用式(9iii)重新生成,随着迭代次数的增加F逐渐变小,在算法进化后期加快收敛到最优解。 3.3.2 自适应交叉概率 CR决定变异后的个体能够进入选择操作的数量。若CR的值较大,则子代从父代个体继承的信息较少,种群的更新主要依赖于变异的过程,能够增加种群多样性,有利于全局搜索;若CR的值较小,则子代的搜索主要集中在父代周围,缩小寻优范围,但会提升收敛速度,有利于局部寻优。CR与F的调整方法基本一致,如式(11)和式(12)所示: CRi,G+1= (11) CRi,1=CRmin+rand·(CRmax-CRmin) (12) 交叉操作即通过一些方案将变异个体与种群父代个体进行混合,产生候选个体。传统的DE算法交叉策略是由交叉率决定保留父代个体或变异个体。这里采用Liu等[14]提出的中心解方法,表达式如下: (13) (14) xCenter,G为第G代的中心解,每次参与变异和交叉操作的有NP个向量粒子,但是在求解G+1代最优值时需要将上一代的中心解加入;xCenter j,G为第G代中心解的变量,且新个体取代了父代个体,和变异个体共同组成实验个体uij,G+1;jr为[1,D]上的随机整数。 选择的主要目的是挑选更优的个体组成子代个体,通常采用“贪婪原则”选择实验个体和父代个体,本文采用传统DE算法的选择策略。对于最小化问题,具有小适应度函数值的个体更优,如式(15)所示: (15) 其中,xi,G+1为经过选择进入下一代的个体,ui,G+1为经过变异、交叉的实验个体,xi,G为父代个体,f(x)为个体适应度值,由于DE算法采用的是“一对一”选择,因此可以保证精英解不会丢失。 算法实现流程图如图2所示。 Figure 2 Flowchart of MsA-DE algorithm图2 MsA-DE算法流程图 为验证MsA-DE算法的性能,选取14个测试函数[15-17]对其进行测试,函数包括单峰和多峰函数,均属于最小优化问题。另外选取DE算法、MDE(Modified Differential Evolution)算法[18]、RMDE(Random Mutation Differential Evolution)算法[13]、HSDE(Hybrid mutation operator and Self-adapting Differential Evolution)算法[19]和本文算法进行比较,对算法优化测试函数的结果进行对比。测试函数的表达式、变量范围和理论最优值如表1所示。 各算法的参数设置如表2所示,均与各自对应文献中的一致。算法的种群规模NP=100,每种算法均独立运行30次,迭代次数为1 500代,记录下5种算法在20维,50维,100维中得到的平均值、标准差,即可对比出算法性能的优劣。 Table 1 14 test functions表1 14个测试函数 Table 2 Parameter settings表2 参数设置 为了更直观地得出结论,采用以显著性水平为0.05的Wilcoxon 秩和检验指标[20,21]和胜率进行进一步分析。Wilcoxon 秩和检验是由Mann,Whitney和Wilcoxon共同设计的一种检验,可以用来检测2个独立样本之间的差异性。它和T检验均可用于测试2组独立样本的差异性,但是T检验要求数据必须符合正态分布且具有相同方差。因而当这2个条件无法确定时,通常采用Wilcox-on秩和检验。检验结果存在2种情况:差异显著和差异不显著。若是有显著性差异无法判断哪个算法性能更优,则需要用“胜率”作为进一步判断算法性能优劣的方案。“胜率”,即将2种算法每次运行得出的最优值两两进行比较,若胜,加1分;若平,加0.5分;若败,加0分。将每个算法得到的分数除以比较的次数(30×30=900次),得到的值就是它们各自的胜率。仿真实验使用Matlab软件编程实现。 根据4.1节所述的参数设置及分析指标,测试函数的优化结果如表3~表5所示。表3中用“+”“-”和“=”分别表示比较算法性能优于、劣于和相近于MsA-DE算法;表4为MsA-DE算法与对比算法的胜率;表5用ARM和ARSTD分别表示算法在平均值和标准差上的平均排名,排名越低则算法性能越好。 Table 3 Experimental simulation results表3 实验仿真结果 续表 表3和表4显示了在20维,50维和100维搜索空间中f1~f14的仿真结果。不难看出,低维时,在函数f1,f3,f4,f8,f9,f13,f14上,只有MsA-DE算法能够精准地找到理论最优值,在f5上MsA-DE与DE算法取得并列最优解,f2,f6,f7上MsA-DE虽然未能找到理论最优值,但是寻优结果非常接近理论最优解,因此MsA-DE算法具有较好的寻优性能。此外,MsA-DE算法的平均值和标准差排名最低,可知MsA-DE算法具有较好的稳定性。在中、高维上,除函数f2,f6和f7外,MsA-DE算法均找到了全局最优解,且MsA-DE算法在所有的测试函数上的平均值和标准差均为最优值,排名最低。由此可知,MsA-DE算法不仅对低维函数有着良好的优化性能,随着维数的升高,MsA-DE算法对于中、高维函数仍然具有较大的优势。 对算法优化性能的评估指标除了最优解的精度还有优化速度,本文采用平均运行时间来评价各个算法的优化速度,如表6所示,加粗字体表示该算法平均运行时间最少。 当2种算法的平均值和标准差相同时,平均运行时间少的算法更有效。 Table 4 Winning rate calculation results of MsA-DE algorithm and other algorithms表4 MsA-DE算法与其它算法胜率计算结果 % Table 5 Average ranking and statistical results of the five algorithms under different indicators表5 不同指标下5种算法的平均排名及统计结果汇总 Table 6 Average running time comparison of five algorithms optimization test functions表6 5种算法优化测试函数的平均运行时间对比 s 由表6可以看出,对于大多数函数,MsA-DE算法的平均运行时间均最短,传统DE算法用的时间最长,特别是在维度升高时,运行时间会大幅增加。例如函数f7,在20维,50维,100维时DE算法的平均运行时间分别为4.3 s,14.7 s和28.6 s,相比于20维,该算法在50维和100维搜索空间的运行时间大幅增加。再比如在20维的函数f5上,MsA-DE算法和DE算法的平均值和标准差相同,因为MsA-DE算法运行时间小于DE算法的,所以MsA-DE算法优化性能更好。 为使MsA-DE算法的效果更加直观,现选取6个测试函数的优化收敛曲线图。图3和图4为20维搜索空间中函数f5,f12的平均收敛曲线,图5和图6为50维搜索空间中函数f6,f10的平均收敛曲线,图7和图8为100维搜索空间中函数f2,f7的平均收敛曲线,横轴表示迭代次数,纵轴表示平均函数值。 Figure 3 Average convergence curve of function f5 when D=20图3 20维搜索空间中函数f5的平均收敛曲线 Figure 4 Average convergence curve of function f12 when D=20图4 20维搜索空间中函数f12的平均收敛曲线 Figure 5 Average convergence curve of function f6 when D=50图5 50维搜索空间中函数f6的平均收敛曲线 Figure 6 Average convergence curve of function f10 when D=50图6 50维搜索空间中函数f10的平均收敛曲线 Figure 7 Average convergence curve of function f2 when D=100图7 100维搜索空间中函数f2的平均收敛曲线 Figure 8 Average convergence curve of function f7 when D=100图8 100维搜索空间中函数f7的平均收敛曲线 由仿真图可知,与对比算法相比,MsA-DE算法的收敛速度最快,而对比算法的收敛速度明显低于MsA-DE的,这说明MsA-DE算法跳出局部最优的能力最强,能够快速准确地找到全局最优解。因此可以得出结论,MsA-DE算法的优化性能明显强于对比算法的,能够有效地增加种群多样性,提高算法找到全局最优解的可能性。 RPC的容量优化问题,就是在满足治理要求的前提下对RPC的补偿容量进行合理配置,使补偿成本最小化的问题。对其进行建模分析,可知属于复杂函数优化问题,因而采用MsA-DE算法对其进行优化。在满足各项约束条件的同时,算出RPC的补偿容量最小值,在电能质量符合标准的同时提高治理系统的经济性。主要包括目标函数的设定和约束条件的处理。 以RPC补偿容量为目标函数,根据补偿策略,将RPC容量配置为: minS=S1+S2 (16) 其中,S1=ΔSa+ΔSb为负序补偿容量;S2=S′a+S′b为谐波补偿容量。 5.1.1 负序补偿 在V/v接线牵引变压器的情况下,令α=ej120°,K为电压器变比,可得正序、负序电流的计算公式为: (17) 其中,IA,IB,IC为网侧三相电流,Ia,Ib为供电臂电流。假设2个供电臂均处于牵引工况下,需要转移的电流有功量为: ΔIP=0.5λ(Ia-Ib) (18) 需要转移的有功功率为: (19) 需要优化补偿的无功功率分别为: (20) a、b供电臂所需的补偿能量分别为: (21) 其中,Pa、Pb分别为补偿前a、b供电臂的负荷有功功率;Iap、Iaq、Ibp、Ibq分别为补偿前a、b供电臂的负荷有功、无功电流;λ为有功转移度,一般取值为[0,1],λ值越大则有功转移量越多,当λ=1时,RPC进行完全补偿;φ为无功补偿度,即优化补偿前后电流间的夹角,取值为[0,π/6]。 5.1.2 谐波补偿 根据优化补偿的思想,将最严重的3,5,7次谐波补偿至国标要求值,其它次数谐波均完全补偿,设a、b供电臂上谐波电流总值分别为Ialh、Iblh,将3,5,7次谐波进行优化补偿后的电流值分别为I′alh,I′blh,则2个供电臂谐波优化补偿所需的谐波能量为: (22) 其中,Ua,Ub分别为a,b供电臂电压。 (23) 综上: (24) 其中,K为变压器变比,εu≤1.2%,SK为公共连接点的三相短路容量,UL为公共连接点的额定线电压,且对于特定的牵引系统,SK、UL已知。 为了验证本文算法的有效性,设计2种工况,利用Matlab建模进行仿真验证。系统仿真参数如表7所示。接在电力机车变压器二次侧的电阻负载为0.7 Ω,不可控整流负载为1 Ω电阻串联1个200 mH电感的阻感负载,用来模拟谐波源。 Table 7 Simulation parameter表7 仿真参数设置 工况1:设a供电臂负载功率为4 800 kW,b供电臂空载。由表8可知RPC补偿前完全补偿所需的补偿能量较大,此时可以由前述方法算得所补偿能量为7.253 MV·A,此时转移的有功量较多,功率因数高,治理效果好但是经济性较差;采用MsA-DE算法进行优化,可得出最优值λ=0.376,φ=11.74°,此时消耗的能量为4.142 MV·A,仅为完全补偿时的57.1%,既满足了电能质量治理条件,又提高了装置的经济性。 Table 8 Compensation result of working condition 1表8 工况1的补偿结果 工况2:设a供电臂负载功率为4 800 kW,b供电臂负载功率为2 400 kW。表9为补偿情况对比。此时的最优点为λ=0.26,φ=15.81°,消耗的能量为3.794 MV·A,仅为完全补偿时的50.2%,且电压不平衡度满足εu<1.2%这一要求。 Table 9 Compensation result of working condition 2表9 工况2的补偿结果 本文提出的MsA-DE算法引入了表示进化程度的阈值,将不同变异操作的优点进行有效结合,提高了算法的寻优能力;采用越界处理方法对变异个体进行改进,保证了种群的多样性;参数的自适应调整可在进化后期快速收敛至全局最优解;扰动机制能够避免算法过早陷入局部最优,弥补了传统DE算法收敛精度低、易陷入局部最优等缺陷。通过对14个Benchmark测试函数和RPC容量优化问题进行实验对比,结果表明,MsA-DE算法是一种有效的优化算法。
3 改进差分进化算法
3.1 变异策略

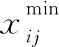
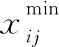
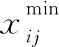


3.2 扰动策略

3.3 控制参数自适应
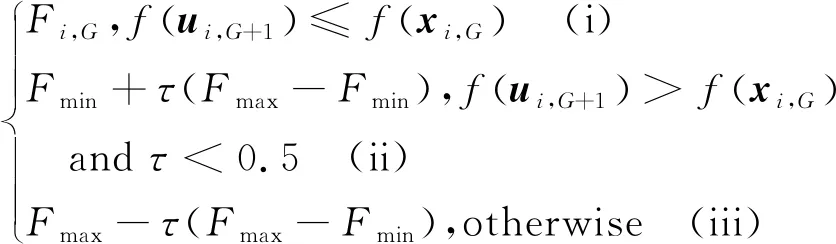

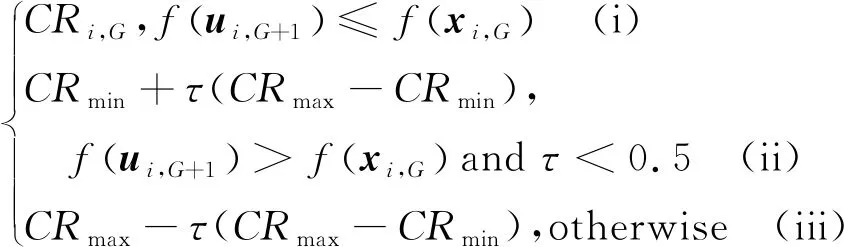
3.4 交叉操作
3.5 选择操作
3.6 算法实现流程图

4 算法仿真测试
4.1 测试函数、性能指标与参数设置

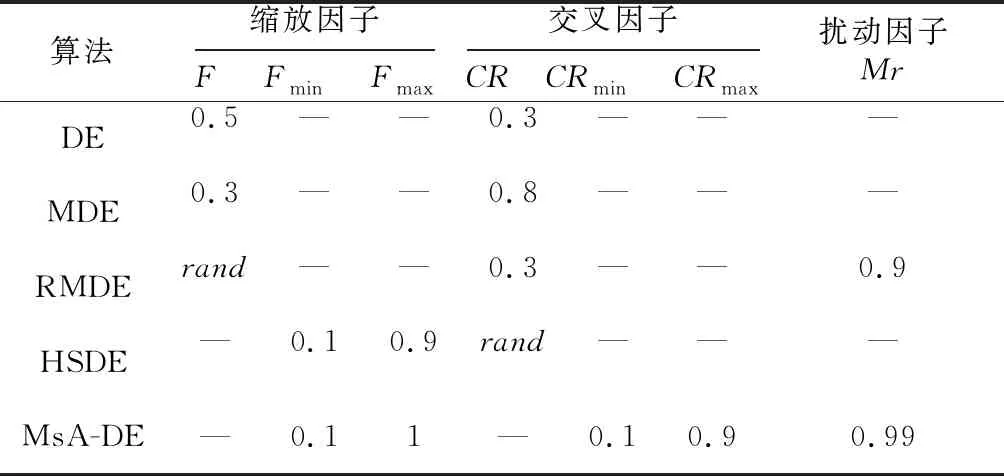
4.2 函数测试结果及对比









5 RPC容量优化模型
5.1 目标函数
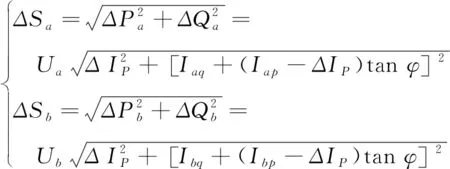
5.2 约束条件
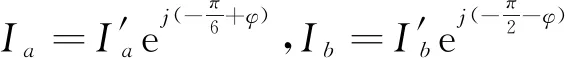
5.3 仿真分析



6 结束语

