碳纤维增强镁基复合材料高温变形微观组织演化研究

白坤举

(鹤壁职业技术学院，河南 鹤壁 458030)

1 试验材料和方法

1.1 试验材料

本文试验中选用的碳纤维增强镁基复合材料为AZ91型合金，该合金由铝、锌、锰、硅等元素组成，增强材料为T300型碳纤维，密度为1.87g/cm3，平均纤维长度为4mm。制备复合材料的方式为真空压力浸渗法，制备工艺为预热540℃、浸渗温度660℃、压力7.5MPa、压力时间20min，最终得到的材料中碳纤维的体积分数为20%。复合材料的密度为1.67g/cm3，致密度为97.5%。

在制备时，首先将碳纤维和AZ91合金制作为8×12mm的圆柱体，并将其放入加热装置中以180℃加热大约2h后在室温中冷却。当材料充分冷却后，对其表面进行打磨，并在热模拟试验机上进行加热实验，温度为400℃，应变速率为0.01s-1，应变量为0.2～0.6，加热升温速率为30℃/s，当温度达到400℃后对材料保温1min，随后进行淬冷。

1.2 计算模拟

(1)分析模型。在有限元分析软件中，建立与圆柱体相关的几何模型并划分相应的网格，对应圆柱状的复合材料，由于要分析复合材料在高温下形变时不同位置的形变效果，因此在模型中设置了3个具有代表性的点，分别位于端面中心、轴线中心和模型表面。由于模型在变形时其中的网格会发生畸变，因此在模型中开启了畸变网格划分模式，边长为0.5mm。

2 试验结果与分析

2.1 动态再结晶模拟

(1)变形量。图1为温度400℃、应变速率0.01s-1时不同变形量下复合材料的再结晶体积分数，从图中可以得知，当变形量逐渐增加时，复合材料的中心最开始发生再结晶过程(图1a)，随后扩展到外围变形区域(图1b和图1c)，当变形量稳定在0.7，高温压缩试验已经基本结束时，中心区和外围变形区的再结晶基本充分，而材料中与压缩头基础不充分的部位则未发生明显的再结晶过程(图1d)。

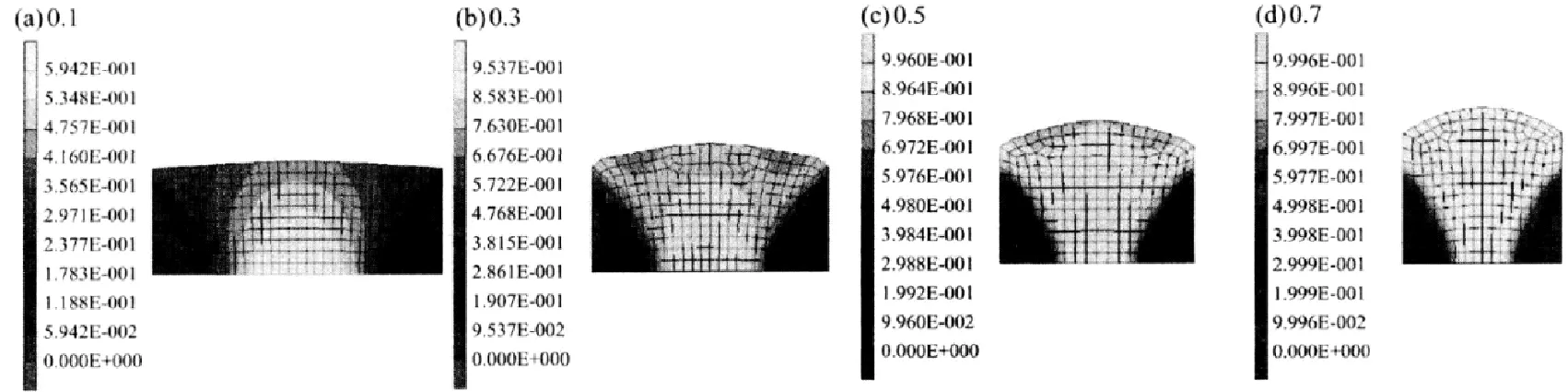
图1 不同形变量下复合材料的再结晶体积分数

图2为模型中的代表性节点A、B、C处的再结晶体积分数随压缩高温时间的变化曲线，从曲线中可以看出，A点基本不受温度的影响，其再结晶体积分数几乎不发生变化，B和C则有明显的再结晶特征，B点的再结晶程度要高于C点。造成这种现象的原因是A点位于试样的断面处，在进行高温压缩试验时，A点会频繁地与压缩头相摩擦，因此难以发生塑性形变；而节点B相对于节点C更靠近试样的中心区，会首先发生变形，变形的程度自然比C点更高。

图2 节点A、B、C动态再结晶体积分数随高温压缩时间的变化曲线

(2)变形温度。变形温度的试验中，将应变速率设置为0.01s-1，变形量为0.7，变形温度则为350℃、375℃、400℃和425℃，测得的复合材料的再结晶状态如图3所示。

图3 不同温度下复合材料的再结晶状态

从图3中可以看出，当温度在350℃，材料中的晶粒并未完全细化，其中有大部分都未结晶；而当温度上升到375℃时，材料中的再结晶过程较为明显，大部分区域都已完成再结晶过程，晶粒相对更为细化，而端面区依旧没有发生再结晶过程。

2.2 实验结果与验证

图4 不同变形参数下复合材料的金相组织

图4为复合材料在温度350～425℃、应变速率0.01s-1和温度400℃、应变速率在0.001～0.1s-1时的金相组织，从图中可以看出，在应变速率相同时，复合材料的再结晶晶粒尺寸随温度的升高而变大，而温度相同时，复合材料的再结晶晶粒尺寸随应变速率的增大有逐渐减小的趋势。此外，在金属和碳纤维连接处，金属晶粒往往比其他区域更加细小，金属原子难以在碳纤维周围聚集。

在实验实证中，实验值的各项数值均小幅高于计算机模拟值，但两者之间的差距不大，基本可以控制在10%(计算机模拟误差要求)之内，这说明本文所使用的计算机模拟方式可以研究碳纤维增强镁基复合材料在高温下的微观组织变形演化模式，可以准确预测高温时不同状态下复合材料的变形状态，具有一定的研究和实用价值。

3 结论

本文对碳纤维增强镁基复合材料在高温下的微观变形趋势进行了研究，使用计算机模拟的方式，利用有限元分析软件进行建模，研究得出复合材料的再结晶尺寸受变形量和温度的影响较大，当变形量和温度增加时，复合材料的变形首先从中心开始，逐渐向外围变形区扩散，材料端面则基本不发生形变，距离中心越近的区域，受形变影响越大。采用计算机模拟实验的方式与真实实验的误差可控制在10%之内，具有研究和应用方向的实用价值。