锂离子在三维骨架复合锂金属负极中的沉积规律

张睿，沈馨，王金福，张强

（清华大学化学工程系，绿色反应工程与工艺北京市重点实验室，北京100084）

引 言

近年，随着各类智能设备以及电动汽车等的蓬勃发展，以锂离子电池为代表的二次电池储能体系得到了广泛使用。然而，锂离子电池体系经过了近三十年的商业应用和发展，其能量密度已经接近理论极限，已经难以满足新兴产业对二次电池更高能量密度、更高功率密度、更高安全性和循环寿命的需求。锂金属因其极高的理论比容量(3860 mA·h·g-1)和极低的氧化还原电极电势(-3.040 V，相对于标准氢电极)成为了最理想的负极材料。基于锂金属负极的锂金属电池(诸如锂硫电池、锂氧电池等)也成为了最受瞩目的新一代高比能二次电池储能体系[1-3]。

然而，现阶段的锂金属电池仍难以实现极高的能量密度和可靠的安全性，其所使用的锂金属负极仍存在诸多的问题和挑战，尤其是不稳定的固液界面膜和复杂的金属锂沉积与溶解行为制约了其实用化。金属锂作为一种极其活泼的金属，当在电化学条件下接触电解质时，会在其表面快速形成一层化学组成极其复杂的膜，即固液界面膜(SEI 膜)，其可传导锂离子并能阻断金属锂进一步与电解质反应发生损耗。然而这层膜往往并不稳定，在金属锂沉积溶解过程中极易破裂，致使更多的金属锂暴露于工作状态的电解质中，进而反应生成更多的固液界面膜，带来不可逆的金属锂和电解质损耗。同时，金属锂的沉积过程容易出现不可控的金属锂枝晶生长，其一方面会大幅增大金属锂与电解质的接触面积生成更多固液界面膜，另一方面也会破坏已有的固液界面膜，甚至刺穿隔膜造成电池内部短路带来安全隐患。枝晶状的金属锂在溶解过程中，也极易形成脱离集流体无法得失电子的死锂，带来容量损失，其随着充放电循环逐步累积最终还会造成金属锂负极的粉化，致使电池寿命大幅缩短。

为了推动金属锂负极的实用化，提出了许多保护策略用以改进锂金属负极，具体包括液态电解质设计与调控[4-7]、聚合物及固态电解质的使用[8-12]、人工保护层或人工固液界面膜[13-15]、三维骨架复合负极等。三维骨架锂金属负极可以提供更高的比表面积，提供更多的电子传递、离子吸附与电化学反应位点，降低金属锂沉积与溶解过程的极化电压[16-28]；可以通过对离子输运通道的调控，抑制金属锂的不均匀沉积与不均匀溶解，减少金属锂枝晶和死锂的出现，提高库仑效率与电池循环寿命[29-31]；还可以通过提供结构支撑，缓解锂金属负极充放电过程中巨大的体积变化，提高电池结构稳定性[32-35]。基于诸多三维骨架实验研究工作，对三维骨架对锂金属负极的作用过程已经有了一定程度的定性理解[31,36-38]。然而，鉴于三维骨架的实验设计往往有着极大的非理想性，同时材料的设计制备与后续实验表征往往难以大批量重复和筛选。因此，三维骨架金属锂负极的结构物性参数对金属锂沉积溶解行为的影响机制一直难以得到直接有效的揭示和定量的描述。如果能够引入理论模拟[39-40]，就有望实现针对特定结构物性参数作用机制进行机理解释和定量分析，进而实现对三维骨架进行合理的理论设计及优化。

1 理论模拟方法

1.1 理论模型

在经典相变理论模型中，两相界面往往难以通过数值模型进行有效描述，这使得相变过程的界面移动追踪难以实现有效的数值模拟计算。相场理论的出现解决了相变界面追踪这一难点，其引入相场序参量(ξ)，将原本两相界面处的突变界面描述为弥散界面，通过相场序参量ξ的取值来界定物相，同时所有物化性质参数也可以表示为ξ 的函数，进而将相变问题的求解转化为含时偏微分方程的求解问题。

本文所研究的相变反应为金属锂的电化学沉积反应，即

涉及的两相即含有锂离子的电解液相和只含有锂原子的锂金属相。引入相场序参量ξ=c/cs，这里c 为空间中某点某时刻时的锂原子浓度，cs=7.69×104mol·m-3为锂金属中的锂原子浓度。即当ξ=1 时，空间中该点在该时刻为金属锂相；当ξ=0时，空间中该点在该时刻为电解液相；当0 ＜ξ ＜1时，空间中该点在该时刻处于相变界面上。需要注意的是，在数值计算过程中，0 ＜ξ ＜1 对应具有一定数值厚度的弥散界面，其并没有实际物理意义。本文的相场模型中忽略了金属锂与电解质反应形成的固液界面膜对金属锂沉积过程的影响。

该体系的Gibbs自由能函数相应地可以表述为

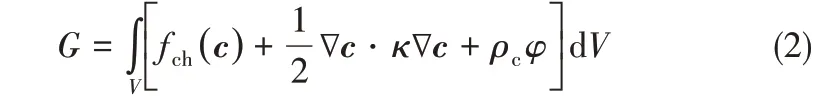
其中，被积函数由亥姆霍兹自由能密度、相场梯度能量密度、静电能量密度三项组成；V 为该体系域中的体积微元；c= {c,c+,c-}，c、c+和c-分别为锂原子、锂离子、电解液阴离子的浓度；κ 为与表面能相关的各向异性相场梯度系数；ρc为电荷密度；φ 为静电势。

锂金属沉积的电化学反应速率由Butler-Volmer动力学方程描述，即

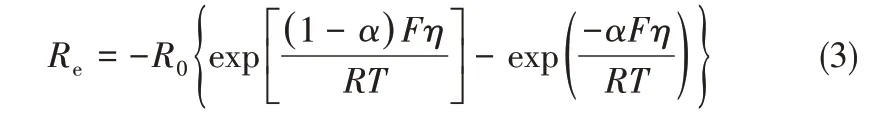
式中，R0为交换反应速率；1- α 和α 分别为氧化反应和还原反应的电荷转移系数；η 为电化学反应过电势；F 为法拉第常数；R 为理想气体常数；T 为温度。

基于Chen 等[44,48]的相场模型推导，可以最终得到用于求解相场序参数ξ的含时偏微分方程为

武成龙和樊虎离开了。白雪心悸地告诉柳含烟：“记得马车被黑白双煞阻拦的事吗？那位在涤尘居门前思索的书生就是见到雪儿要黑白双煞让路的人，从两人的神情该是以为雪儿与那书生别有渊源心生忌惮，因为我哥说能要黑白双煞让路的人凤毛麟角。”柳含烟愕然道：“既然如此你为何不接受他的赠予？”白雪沮丧地道：“嫂子穿上罩袍与那书生身上的相似，所以不想那书生由此看轻雪儿，也坚信少林掌门获悉必然援手。可这会儿……希望还来得及。”

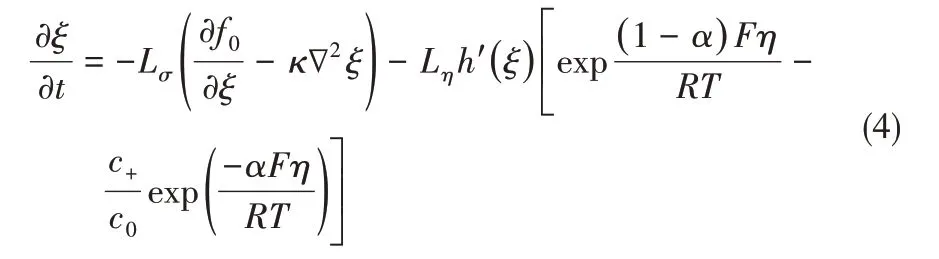
式中，Lσ为反映金属锂表面能和固相扩散的界面迁移系数；Lη为反映电化学反应速率的反应系数；f0(ξ)=Wξ2(1-ξ)2为描述金属锂与电解液两相平衡的势垒函数，其势垒高度为W/16；h(ξ)=ξ3(6ξ2-15ξ+10)为插值函数；η 为电化学反应过电势；c0为电解液体相的锂离子浓度。

同时考虑电迁移、浓差扩散、电化学反应消耗的用于求解锂离子浓度c+的含时偏微分方程为

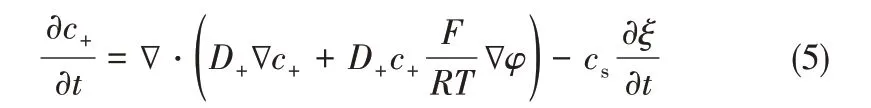
式中，锂离子扩散系数D+= D+sh(ξ) + D+l(1-h(ξ))，D+s和D+l分别为金属锂相和电解液相中的锂离子扩散系数。

此外，静电势可基于泊松方程进行求解，即

其中，电导率σ = σsh(ξ) + σl(1- h(ξ))，σs和σl分别为金属锂相和电解液相中的电导率。

1.2 计算方法

本文中相场模型模拟计算尺寸均为20 μm ×20 μm，为比较不同比表面积下金属锂的沉积行为异同，每个模型底部按照不同比表面积设定了不同的方形凸起。所有模型中方形凸起均为10 μm 高，除特别说明外，所有模型整体孔隙率保持一致，即p=75%，当改变模型中骨架结构尺寸时，可呈比例地提高或降低骨架结构能够负担的沉积容量，同时仍适用最后总结的沉积反应过程机理。经过分析，等间距分布与随机分布初始形核位点，其沉积规律和锂离子浓度变化规律都是一致的。集流体表面以2.5 μm 的平均间距分布初始金属锂沉积位点。三维骨架金属锂负极的比表面积(SA)定义为集流体局部总表面积与集流体横截面面积之比，单位为cm2·cm-2，即无量纲[43]。

使用COMSOL Multiphysics 5.4 对式(4)～式(6)进行最终求解，得到相场序参数、锂离子浓度、静电势的空间分布及时间分布。模拟计算中所使用各物性参数见表1[43-45]。

2 结果与讨论

2.1 三维骨架金属锂负极中金属锂沉积过程

以图1(a)所示三维骨架金属锂负极为例，其集流体方形凸起尺寸为高10 μm，宽5 μm，并以10 μm等间距分布。可知模型范围内集流体总表面长度为60 μm，而集流体横截面即模型宽度为20 μm，则此三维骨架比表面积SA= 3.0。为了方便后续定位比较不同位点的金属锂沉积速率及形貌，在模拟沉积过程之前，集流体表面已以2.5 μm 的平均间距分布了初始金属锂沉积位点，其中包括随机间距的分布，以证明间距是否产生影响，如图1(a)～(c)为等间距分布方式，图1(d)～(f)为随机间距分布方式。

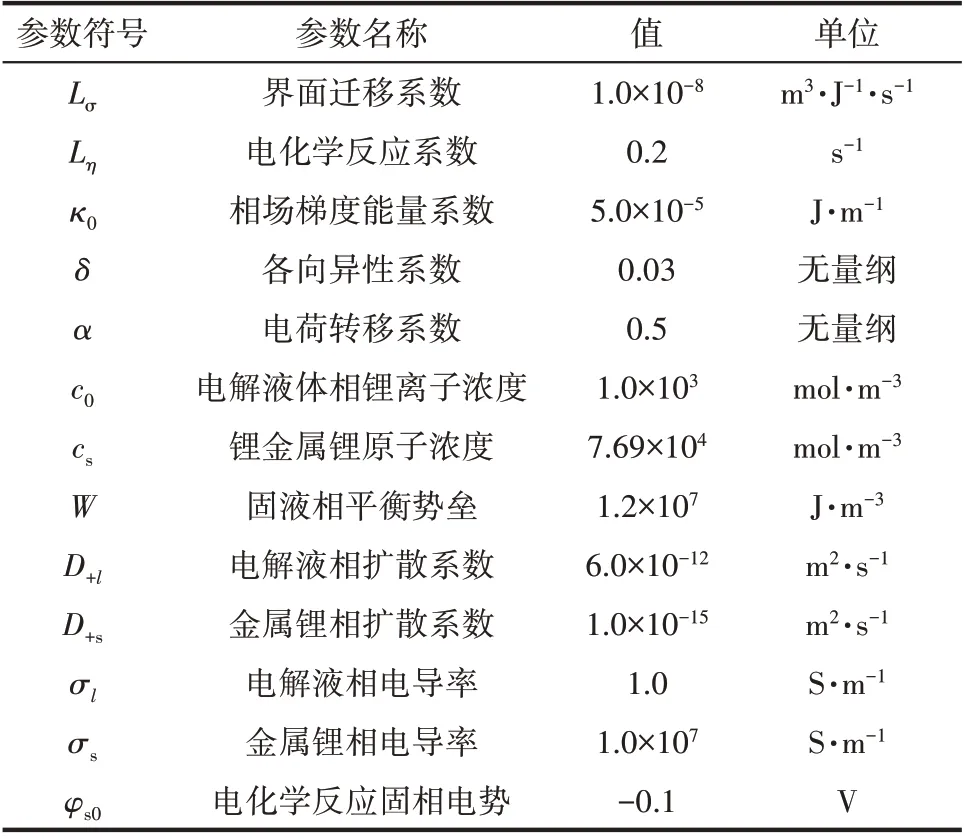
表1 相场模型计算参数Table 1 Parameters in phase field model

当沉积开始后，沉积容量(Q)增加至0.5 mA·h·cm-2后，集流体表面的所有金属锂沉积位点都发生了金属锂电化学沉积反应[图1(b)、(e)]。三维骨架顶部沉积位点相比骨架底部沉积位点，其金属锂沉积速率要稍快一些。在该沉积容量下，金属锂沉积形貌主要体现在沉积位点由小变大，尚未出现明显的枝晶状金属锂沉积。当沉积容量进一步增加至1.0 mA·h·cm-2，三维骨架顶部与底部的沉积速率和形貌都有了非常明显的区别[图1(c)、(f)]。顶部金属锂的沉积速率要远远高于底部的金属锂，并且出现了各向异性的金属锂枝晶状沉积。而底部的金属锂沉积位点在后期沉积过程中并没有明显的体积变化，底部的金属锂沉积速率大幅降低。

造成三维骨架顶部与底部沉积速率差异的主要原因是电解液中锂离子的输运限制。结合该沉积过程中的锂离子浓度分布变化，可以很容易观察到锂离子输运在调控金属锂沉积上的关键作用(图2)。在沉积开始时刻，电解液中处处锂离子浓度都为1 mol·L-1，此时各个金属锂沉积位点具有相等的沉积速率。

随着金属锂的沉积，三维骨架孔隙中电解液的锂离子浓度出现下降，意味着锂离子自顶向下的输运速率已不足以支撑其在侧面集流体表面发生锂离子还原反应的消耗。当沉积容量增至0.5 mA·h·cm-2时，孔隙中央的电解液锂离子浓度已下降至0.6 mol·L-1，而当沉积容量进一步增至1.0 mA·h·cm-2时，孔隙中的电解液锂离子浓度已低于0.2 mol·L-1，此时三维骨架底部已不足以进行有效的金属锂沉积反应。与此同时，在电迁移与浓差扩散双重驱动下输运而来的锂离子，将会优先在三维骨架顶部的沉积位点上还原生成金属锂。因此，三维骨架在后期的金属锂沉积过程中，其顶部和底部会出现较大的沉积速率与形貌差异。此外，研究发现无论是等间距的初始形核位点，还是随机间距的初始形核位点，其沉积规律和锂离子浓度变化规律都是一致的。

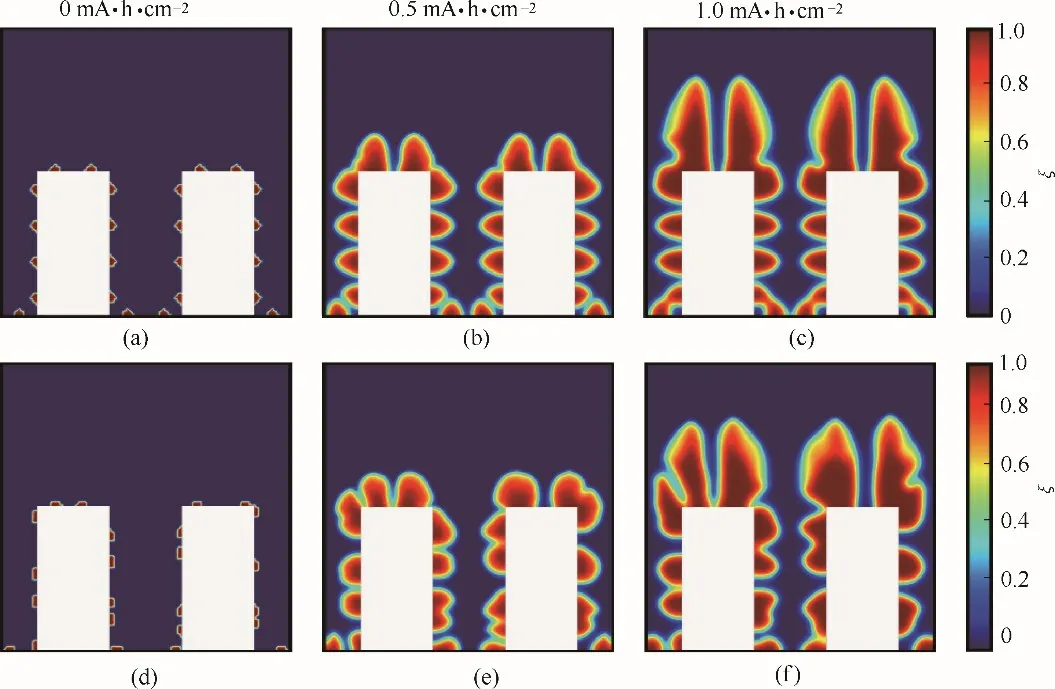
图1 三维骨架金属锂负极沉积过程相场序参数分布Fig.1 Phase field order parameter evolution during electroplating process in 3D structured lithium metal anode

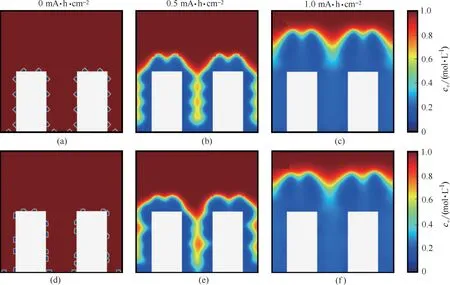
图2 三维骨架金属锂负极沉积过程锂离子浓度分布Fig.2 Li ion concentration evolution during electroplating process in 3D structured lithium metal anode

2.2 不同比表面积的三维骨架负极中的金属锂沉积过程

在不同的比表面积SA下，三维骨架金属锂负极中的金属锂沉积形貌呈现出显著差异。图3列出了比表面积SA分别为1.5、2.0、3.0 和5.0 的不同条件下，沉积容量Q 都达到1.0 mA·h·cm-2时的金属锂沉积形貌。由于初始形核位点的间距分布方式不影响模拟结论，此处及之后的模拟计算均采用等间距分布金属锂初始形核位点的模型进行计算。

在不同比表面积下，三维骨架顶部的金属锂沉积位点都有着很高的沉积速率，并很快生长为枝晶状金属锂。在集流体拐角处，金属锂沉积位点具有最高的沉积速率。这得益于集流体拐角处可以更多地吸收到从体相迁移扩散而来的锂离子。因此，拐角处易快速生长出各向异性的金属锂枝晶。对于三维骨架底部的金属锂沉积位点，可显著观察到比表面积对底部沉积位点沉积速率和形貌的影响。当比表面积SA仅为1.5 时，三维骨架底部的金属锂沉积位点仍有较大机会获得从体相电解液迁移扩散而来的锂离子。因此，其底部也会有金属锂枝晶状沉积的出现。当比表面积SA提高至5.0 时，三维骨架底部的金属锂沉积位点只能生长为很小的球粒沉积，并且无法进一步生长。事实上，对于控制孔隙率恒定为75%的三维骨架，越高的比表面积意味着越小的孔道直径，而越小的孔道直径越难以向孔道中及时补充被消耗的锂离子。比表面积越大、孔道越小的三维骨架材料，其会更容易进入锂离子输运成为限速步的锂离子沉积过程。

2.3 三维骨架负极比表面积对金属锂沉积过程的两阶段作用机制

为了进一步定量探究比表面积对金属锂沉积过程的作用机制，引入了电化学沉积阻力(r)来反映三维骨架在一定沉积容量下进一步进行电化学沉积的难易程度。电化学沉积阻力r = U/ J，单位为Ω·cm2，其中U和J分别为三维骨架在一定沉积容量下进一步进行电化学沉积过程时实验测定或模拟计算所使用的电池电压和电流密度。较低的电化学沉积阻力，意味着在恒流充电条件下，其仅需要较低的过电势驱动即可发生对应恒流当量的电化学沉积；亦即在恒压充电条件下，其发生电化学沉积的反应速率会更高，即表现更高的充电电流密度。电化学沉积阻力主要由两部分构成，一部分是有限表面积提供的有限电子交换速率，较高的比表面积一定程度上可以降低电化学沉积阻力，另一部分是有限离子输运通道的有限离子输运速率，较小的孔隙直径往往会增大电化学沉积阻力。

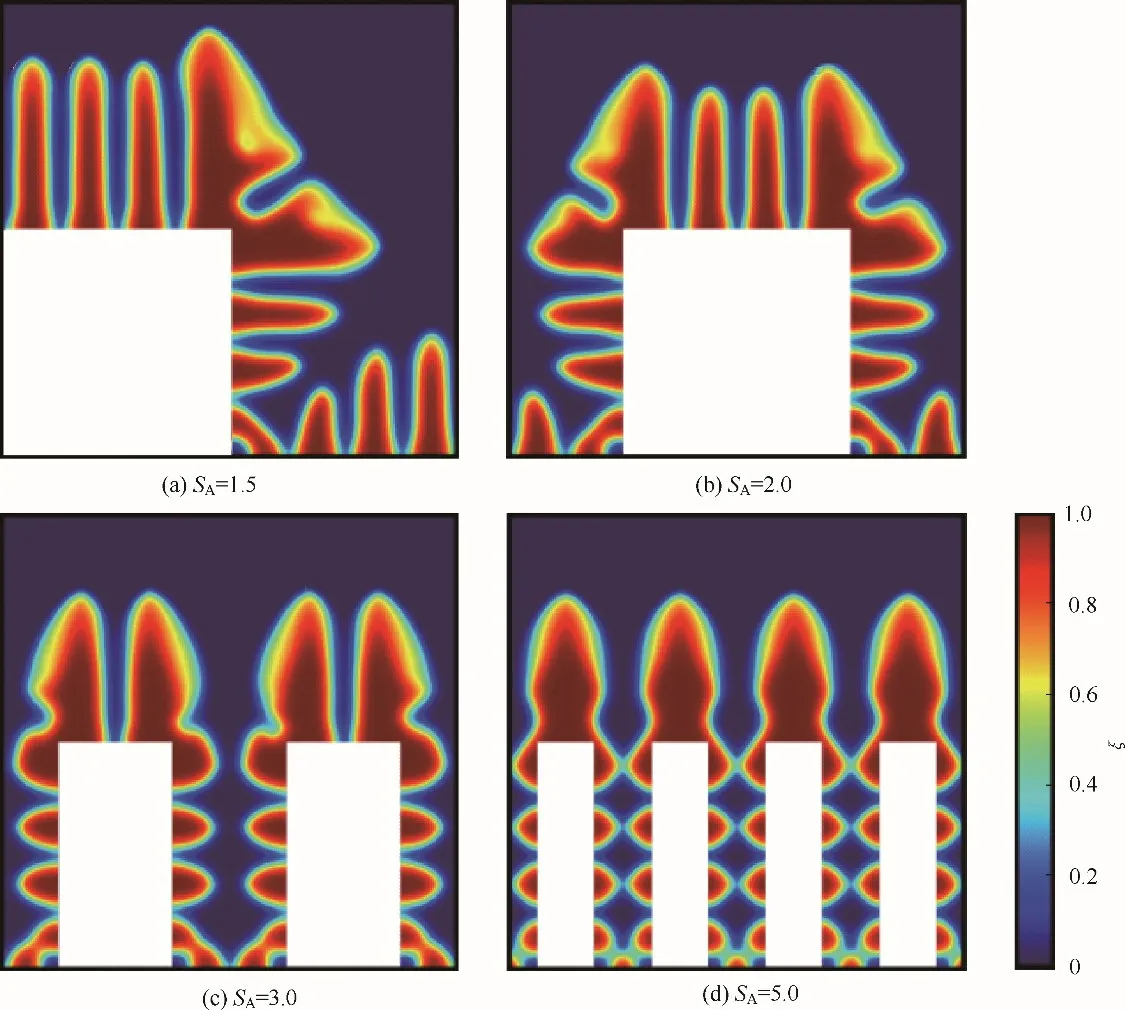
图3 不同比表面积的三维骨架金属锂负极金属锂沉积形貌Fig.3 Lithium electroplating morphology in 3D structured lithium metal anodes with different areal surface area

图4 电化学沉积阻力随沉积容量变化曲线Fig.4 Electroplating resistance varies with electroplating capacity

对上述四种比表面积的三维骨架金属锂负极沉积过程，得到了在不同沉积容量下的电化学沉积阻力变化曲线如图4 所示。随着沉积容量的增加，其电化学沉积阻力均在减小。在前期阶段，其电化学沉积阻力主要来源于有限的表面积提供的有限电子交换速率。而金属锂沉积后期，其电化学沉积阻力主要来源于有限的离子输运通道提供的有限离子迁移扩散速率。在前期阶段，随着比表面积的提高，电化学沉积阻力在降低，而在后期阶段，随着比表面积的提高，电化学沉积阻力反而在升高。截取沉积容量Q 为0.1、0.5 和0.9 mA·h·cm-2时的电化学沉积阻力如图5 所示。当沉积容量为0.1 mA·h·cm-2时，随着比表面积SA从1.5 提高至5.0，其电化学沉积阻力由5.4 降低至4.6 Ω·cm2；而当沉积容量为0.9 mA·h·cm-2时，随着比表面积SA从1.5 提高至5.0，其电化学沉积阻力反而由3.3 升高至4.0 Ω·cm2。在前期阶段，高比表面积可以提供较多的电化学反应位点，总体上降低电化学反应过程所需的反应过电势，因而可以降低电化学沉积阻力。在后期阶段，高比表面积的恒定孔隙率三维骨架其孔道直径大幅减小，使得三维骨架底部难以获得来自体相电解液的锂离子补充，仅三维骨架顶部较少的位点可以进行高效电化学反应，因而整体电化学沉积阻力反而升高。如果保持比表面积不变，仅改变孔隙率，如图4中所示虚线为孔隙率由75.0%降至62.5%的情形，可见其仍然存在明显的两阶段沉积过程，并且由于孔隙率降低，孔道容积减少，由前期阶段过渡到后期阶段的临界沉积容量也由75.0%时的0.5 mA·h·cm-2相应减少至62.5%时的0.4 mA·h·cm-2。

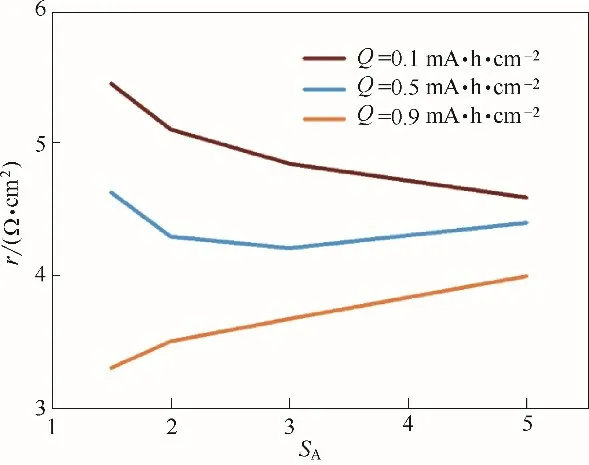
图5 电化学沉积阻力随比表面积变化曲线Fig.5 Electroplating resistance varies with areal surface area

因此，三维骨架负极比表面积对金属锂沉积过程的作用机制主要分为两个阶段，在孔隙锂离子浓度尚未耗到底点的前期阶段，高比表面积提供更多的电化学反应位点，可以降低电化学沉积阻力，有利于金属锂负极的高倍率循环。而当孔隙锂离子浓度消耗至底点进入后期阶段，高比表面积可能会带来较低的孔隙直径，使得离子输运过程受限，反而提高电化学沉积阻力。因此，尽量提高三维骨架负极孔隙容量，使得三维骨架工作状态尽量保持在前期阶段，避免孔隙锂离子浓度耗尽情况的出现，可以最大程度发挥三维骨架负极的优势。

3 结 论

本工作采用相场理论对三维骨架金属锂负极中金属锂沉积进行机理探究。(1)通过相场理论模拟三维骨架中金属锂的沉积过程，直观分析三维骨架顶部与底部金属锂沉积行为和锂离子浓度分布演变。(2)结合沉积形貌和电化学沉积阻力定量分析，总结出三维骨架负极的比表面积对金属锂沉积过程的两阶段作用机理，即孔隙锂离子浓度耗至底点前的前期阶段，高比表面积提供更多电化学反应位点有利于降低电化学沉积阻力；而当孔隙锂离子浓度耗至底点后的后期阶段，高比表面积可能带来较小的孔隙直径使离子输运受限从而提高电化学沉积阻力。(3)指导三维骨架的更高效合理的设计，在选取合适比表面积的基础上，通过提高孔隙容量使三维骨架在充放电循环的工作状态中尽量保持在孔隙锂离子浓度未耗尽的前期阶段，从而最大程度发挥骨架结构对金属锂负极沉积过程的积极调控作用。

在锂金属电池等高比能二次电池研究领域中，还有很多诸如锂枝晶生长溶解机理、固液界面膜生长破裂失效机理等尚难以通过实验研究探明其作用机理。实验方法和理论计算的结合，可以帮助研究者们获得更多机理方面的理解甚至获得可靠的定量结论，这将给包括三维骨架优化设计等锂金属电池的研究工作提供更多更有效的设计理念和指导思想，并争取早日实现高比能高安全性的锂金属电池的实用化。