基于增广误差系统的导弹预见跟踪控制

代子丰 任启峰 高存臣

（中国海洋大学数学科学学院，山东 青岛266100）

1 概述

随着现代技术的发展，精确制导武器成为各个国家在军事发展中的优选目标，如何控制导弹精确打击目标成为越来越多国家研究的热点课题。传统导弹控制系统是把导弹的当前状态与预定弹道比较得出偏差[1]，进而计算控制量，由执行机构控制减少偏差。

导弹制导律的选择对于导弹能否精确打击目标至关重要，目前比较经典的制导方式有：比例制导律[2]、最优制导律[3]以及滑模制导律[4]等。尽管滑模制导律由于其优良的鲁棒性和自适应性被越来越多的应用到导弹制导中[4-6]，但其局限性也十分明显。

预见跟踪控制是在最优控制的基础上发展而来，到目前为止求解方法主要有三种[7]：偏微分最优化法、增广误差系统法和逐次最优化法。其中增广误差系统法是最为常用的方法。

2 模型建立

系统离散化后加入扰动可以得到[9]：

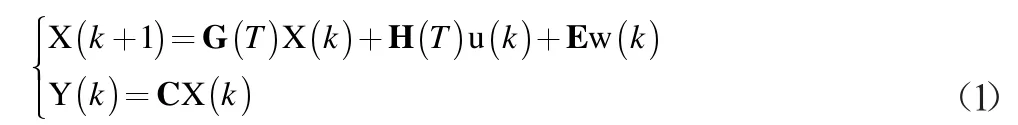
构造辅助变量，定义如下新的变量：

根据上述系统，可以得到：

可以得到：

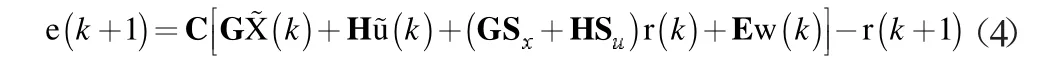
构造向量和新的矩阵可以得到：

由于闭环系统不包含积分器，不利于消除静态误差，为此引入了离散积分器[7]。

3 预见控制器设计

可以将系统化为如下闭环系统：

引理1[2]：系统x（k+1）=Ax（k）渐近稳定的充分必要条件式存在P＞0 使得

则系统（20）是渐近稳定的，其中状态反馈增益矩阵为K=YM-1。