考虑渗压的二长花岗岩流变损伤本构模型研究

李 尧，王 伟*，王如宾，朱其志，王 辉，刘志航

(1.河海大学 岩土力学与堤坝工程教育部重点实验室，江苏 南京 210024；2. 河海大学 土木与交通学院岩土所，江苏 南京 210024)

岩石流变模型是岩石力学研究的一大重点，也是进行流变数值计算的基础。元件模型是岩石流变本构关系研究中不可或缺的一部分，通过对元件进行串并联组合，模拟岩石的流变力学特征。由于元件模型概念直观、物理意义明确，并可以模拟岩石的多种力学效应，且易编程实现、应用方便，近年来对岩石元件模型的研究取得了大量成果,获得的改进元件模型可以很好地反映岩石流变非线性特性[1-9]。考虑渗压作用的流变损伤本构模型研究成果较少，本文通过对二长花岗岩流变试验数据的研究，在广义Bingham模型的基础上建立了基于渗透压力损伤的流变损伤本构模型，并进行了参数辨识，对所得结果和试验结果相比较，本文建立的考虑渗压损伤的非线性流变本构模型与试验曲线拟合效果较好，验证了所建立的非线性流变本构模型的合理性。

1 岩石流变损伤本构模型及参数辨识

1.1 Biot系数的确定

在多孔介质弹性理论框架内，一般采用有效应力原理分析流固耦合问题，有效应力可表示为：

(1)

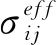
Terzahi[10]在土力学中提出有效应力原理，其后Biot[11-12]在饱和多孔介质的本构机制方面进行了开创性的研究。考虑到有效应力系数对有效应力确定的重要性，国内外众多学者已开展了不同围压和渗压下岩石的渗透性试验研究，获得了基于渗透系数的岩石有效应力系数。

综合国内外有关渗透系数与有效应力关系的试验成果，借鉴文献[13]，渗透系数k可以表示为有效应力的单值函数：

(2)

Cross-plotting[14]法是由J.B.Walsh提出的，根据达西公式计算得到岩样在不同压力状态下渗透率的一种方法，基于式(2)并根据Cross-plotting法确定岩石的有效应力系数，当渗透系数相同时，有效应力亦相同，基于岩石渗透系数的试验结果，可获得恒定围压下，渗透系数随孔隙压力变化的演化规律。再取一系列渗透系数作为参考值，针对同一渗透系数，可以获得一系列围压和孔隙压力的组合，通过恒定围压和孔隙压力拟合线性关系的斜率最终得到Biot系数。不同压力组合下的平均渗透系数见表1。图1和图2为根据Cross-plotting方法测得的有效应力系数。

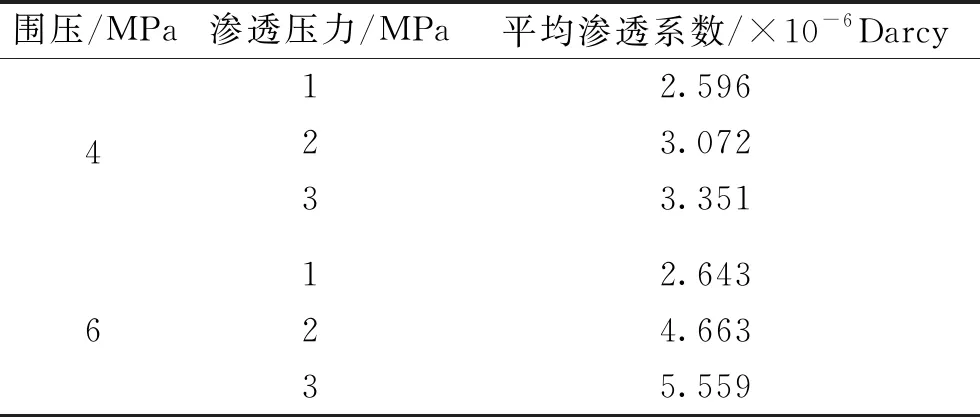
表1 不同压力组合下二长花岗岩的渗透系数表

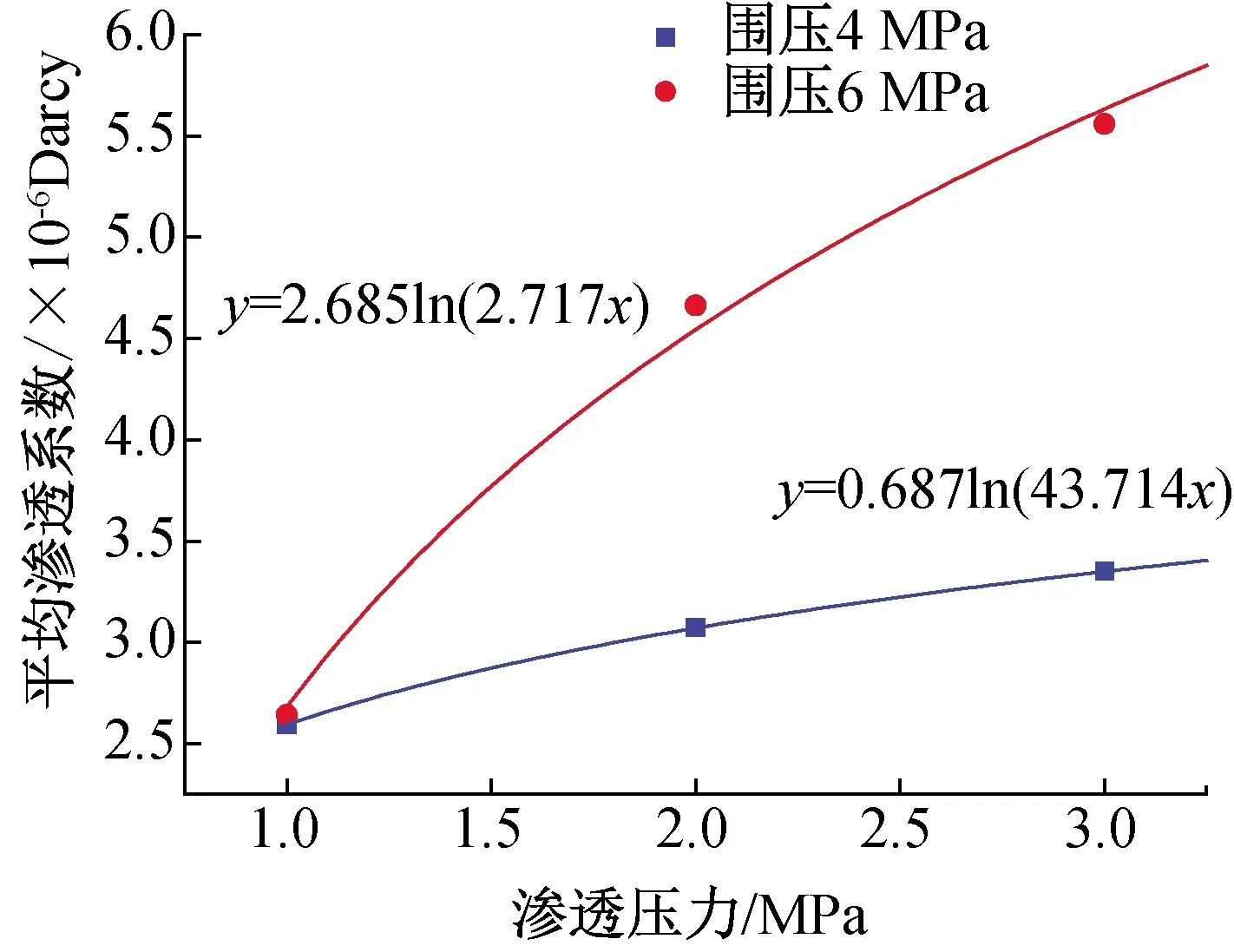
图1 渗透压力-平均渗透系数关系曲线Fig.1 Permeability pressure-average permeability coefficient relation curve

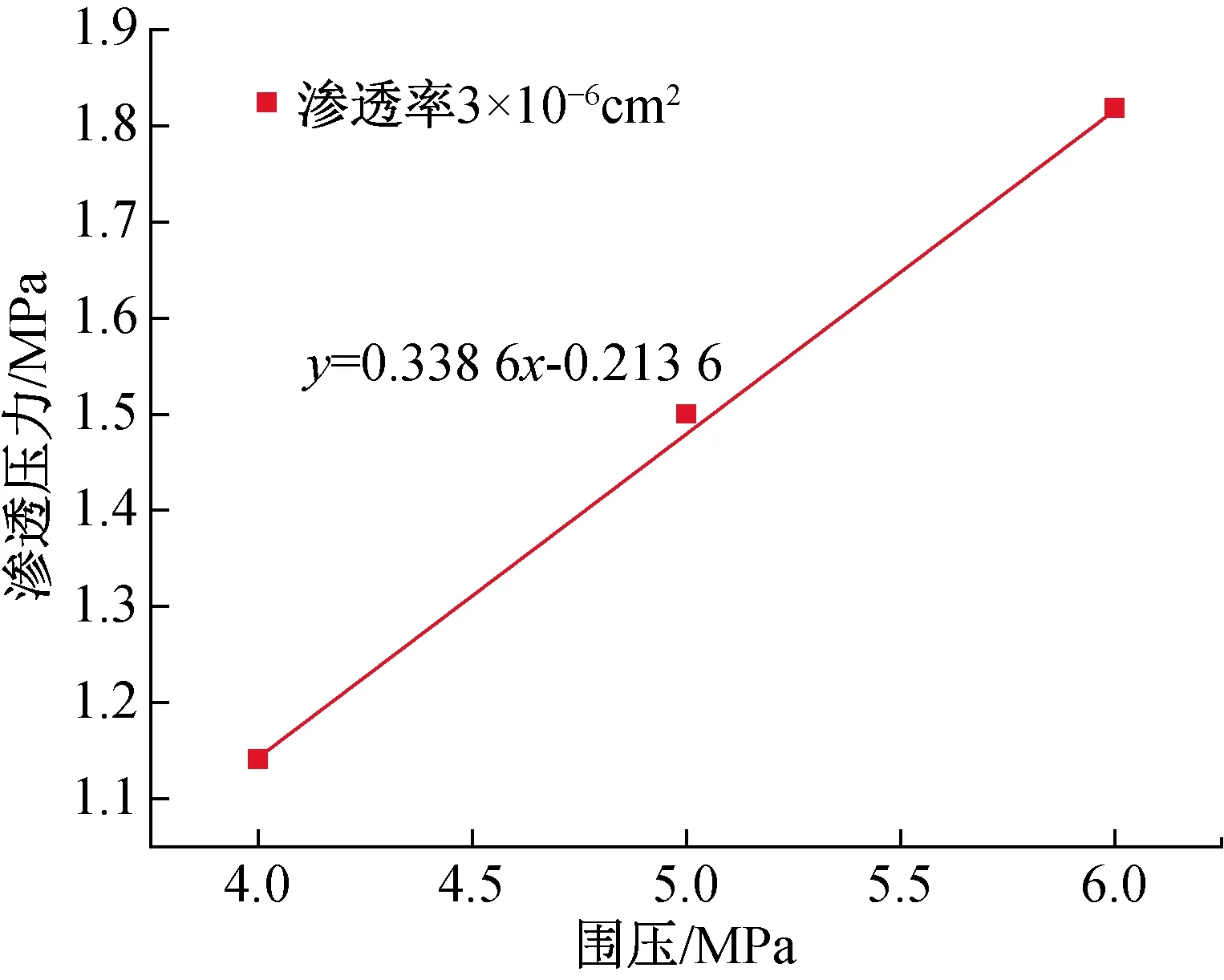
图2 孔隙压力-围压的关系曲线Fig.2 Pore pressure-confining pressure relation curve

根据对大量的试验结果的分析，取均值渗透系数3×10-6Darcy时Biot系数，如图1中所拟合的渗透系数与恒定围压的关系中，差值得到相同渗透系数下不同控制压力作用下的渗透压力，由Cross-plotting方法，得到孔隙压力与围压的关系曲线，其斜率即为Biot系数，由图2的拟合结果可知，弹性阶段的Biot系数为0.338 6。

对各向同性材料而言，Biot系数是各向同性的。然而在脆性岩石破坏过程中，其中裂纹萌生、扩展直至贯通是各向异性的过程，裂纹主要沿主应力方向发展，导致Biot系数变为各向异性，因此对塑性变形后期由于试样中裂纹已经完全贯通，形成宏观裂纹，所研究的岩石为裂隙孔隙材料时，可以采用裂隙内的孔隙水压力代替岩块内部的孔隙水压力，仍可认为此时的Boit系数为1。

1.2 考虑渗压的损伤分析

在不同渗透压力作用下岩石粘聚力和内摩擦角等力学特性会发生不同程度的变化，渗透压力会促进裂纹的产生和发展，因此在岩石流变过程中围压、偏应力和温度相同的情况下，渗透压力的变化对岩石损伤的影响不容忽视。

损伤变量通常用D来表示，材料的损伤使其内部承受的净应力σD大于实际应力σ，净应力可表示为：

(3)

损伤变量D可以定义为应变的函数：

(4)

由广义胡克定律，可以得到：

ε=ε1-(1-2μ)σ3/E

(5)

式中:μ为泊松比，E为弹性模量。

将式(5)代入式(4)中，可以得到：

(6)

根据有效应力原理，在稳定渗压作用下岩石应力可用式(1)表示，因此将式(1)代入式(6)中可得有效应力作用下的损伤变量D：

(7)

损伤不仅与围压和偏应力有关，在不同渗压作用下亦与渗压大小有关，是各个应力共同作用的结果，因此，需在式(7)中引进一个渗透压力的函数。根据不同渗透压力条件下，内摩擦角和粘聚力的变化规律可知，随着渗压的增加，均成线性变化，因此假设损伤参数m与渗压有如下的关系：

m=apw+b

(8)

式中：a,b为试验参数。

将式(8)代入式(7)中可以得到考虑渗透压力的损伤变量D：

(9)

考虑到有效应力系数在岩石流变过程中不是恒量，做如下假定，在衰减流变阶段和稳态流变阶段，由于裂纹发展缓慢，有效应力系数取为0.338 6；而在加速流变阶段，有效应力系数取为1，可由应变阀值ε0进行控制。

1.3 改进的广义Bingham模型的流变损伤模型

线性粘弹性模型可很好地模拟岩石流变的衰减流变阶段和稳态流变阶段，但当岩石偏应力到达某一等级时，岩石会发生加速流变破坏，因此存在一个应力阀值，当偏应力等级小于该值时，将发生前两个阶段的流变；当外荷载水平达到应力阀值时，将发生三个阶段的流变。本文将裂隙体积应变的转折点作为裂隙开裂的起始应力阀值，岩石从此时开始发生损伤。综合试验结果，考虑使用广义Bingham模型对岩石的流变进行描述(图3)。

图3 广义Bingham模型Fig.3 Generalized Bingham model

典型的广义Bingham模型的计算公式如下(本文取轴向应变为主要的研究对象)：

(10)

根据文献[15]的研究成果，对于广义Bingham模型，定义一个描述流变衰减阶段和稳态阶段的非线性函数：

f(t)=1-e-nt

(11)

当n为某一合适参数时，当t达到某一时刻时，f(t)=1，可以很好地描述衰减流变和稳定流变阶段。当偏应力等级大于阀值σs时，岩石发生加速流变破坏，通过引入损伤，在粘塑性元件中采用净应力代替Cauchy应力，可以很好地描述岩样的加速流变过程。因此改进的广义Bingham模型建立的过程如下：

(1) 在偏应力等级小于岩石的应力阀值时，损伤没有发生，因此D=0，岩石的流变方程为广义Bingham模型。

(12)

(2) 当偏应力等级大于岩石的应力阀值时，但未发生加速流变破坏时，应该考虑损伤对岩石流变的作用，此时裂纹并未出现，因此有效应力系数取为0.338 6，则流变损伤方程为：

(13)

净应力可根据式(1)和式(9)得到：

(14)

(3) 当偏应力等级大于岩石的应力阀值，且发生加速流变破坏时，此时由于宏观裂纹逐渐出现，因此有效应力系数取为1，流变方程与式(13)相似，净应力可以表示为：

(15)

根据式(11)—(13)可以看出，考虑渗压损伤的流变本构模型主要参数包括弹性模型E、泊松比μ，有效应力系数β和表征渗压影响的系数a和b。弹性模量和泊松比可通过加载过程中的瞬时应力和应变确定，有效应力系数按照1.1节假设确定，a和b可通过拟合最后一级偏应力试验曲线获得，应力阀值可以通过相同试验条件下瞬时试验体积应变规律确定，加速流变起始点应变可通过最后一级流变速率曲线获得，至此所有的流变参数均已确定。采用以上本构关系得到的材料参数如表2—表4所示。

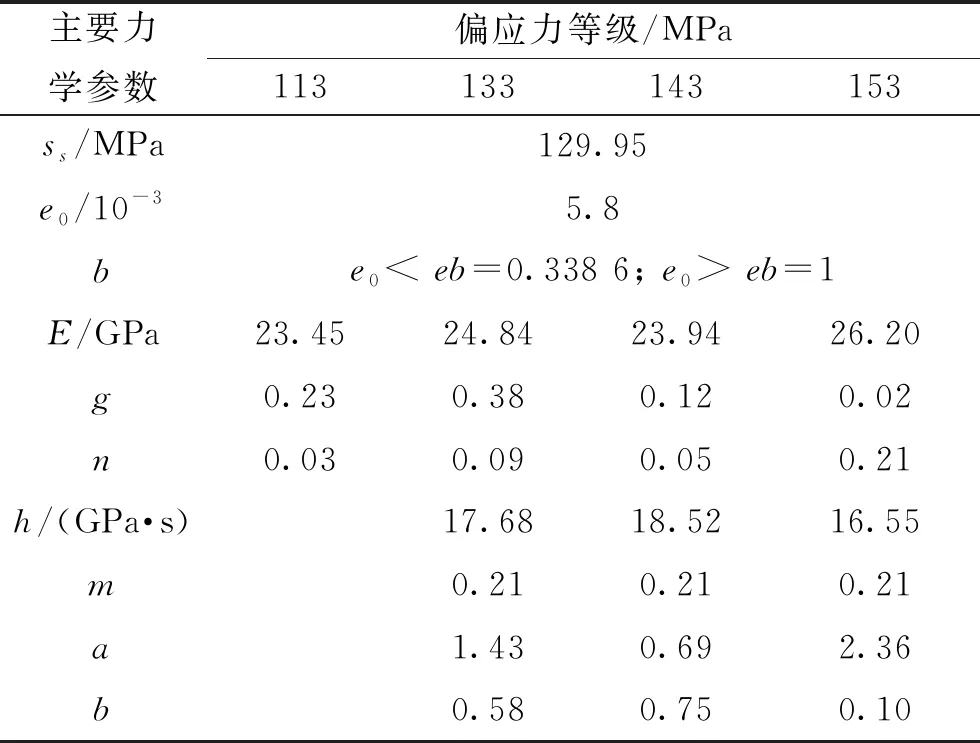
表2 围压4 MPa、渗压1 MPa状态下模型力学参数表

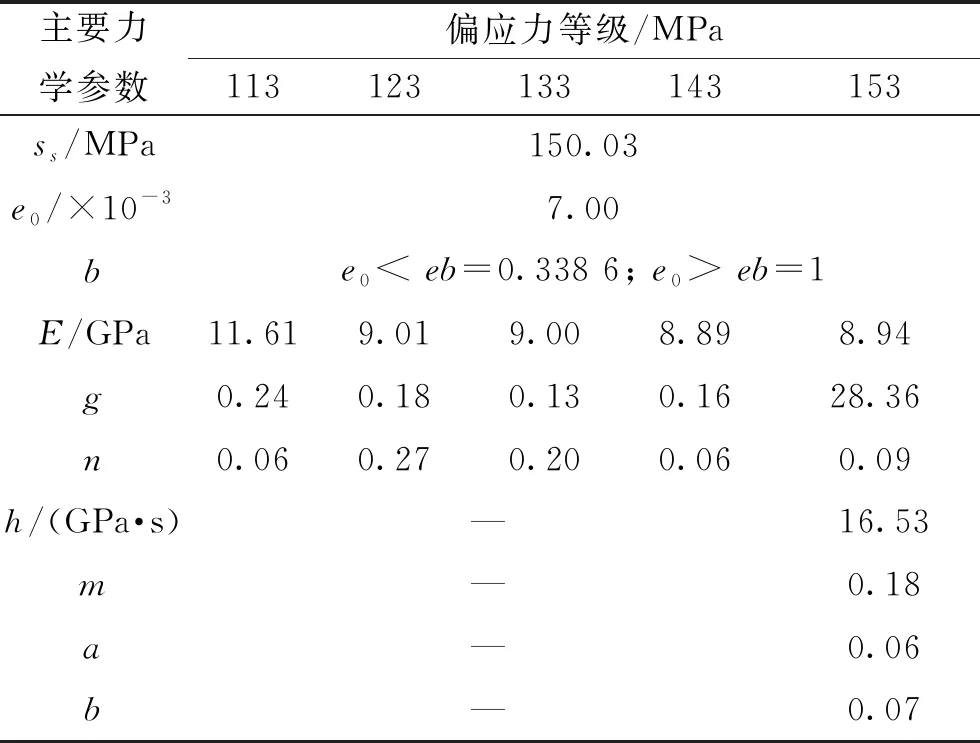
表3 围压4 MPa、渗压2 MPa状态下模型力学参数表

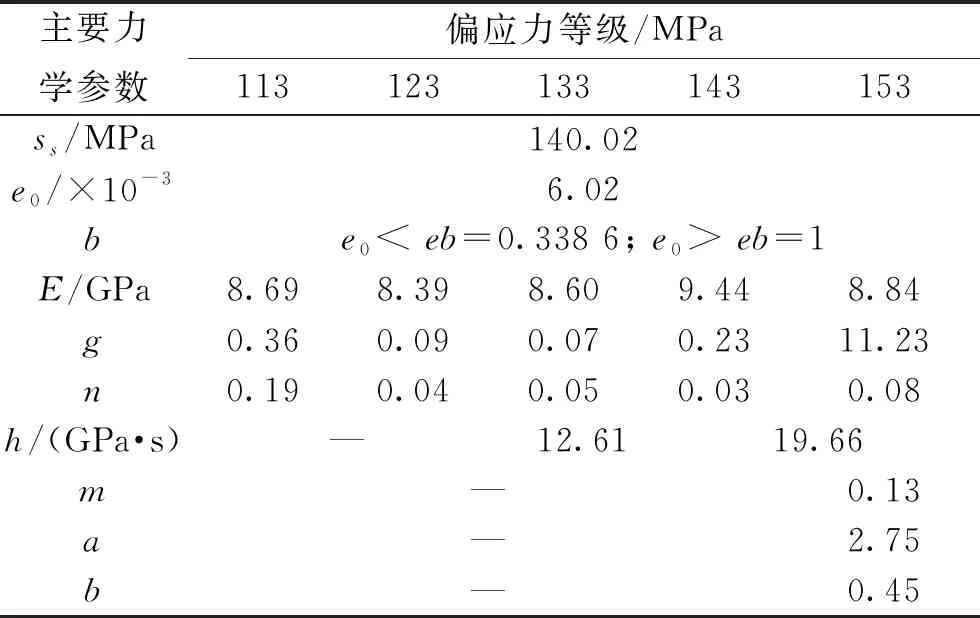
表4 围压4 MPa、渗压3 MPa状态下模型力学参数表

2 考虑渗压的流变损伤本构关系验证

根据试验结果分别作出了围压为4 MPa时不同渗压条件下试验曲线与拟合曲线的对比图，其中，渗压为1 MPa条件下作出了全过程流变拟合曲线图，为了更加清晰地对比加速流变阶段的拟合效果，在渗压为2 MPa和渗压为3 MPa条件下给出了最后一级荷载作用下(即加速流变阶段)的拟合曲线，如图4所示。

由图4可见，本文建立的考虑渗压损伤的非线性流变本构模型与试验曲线拟合效果较好，由图4可以看出模型可以较好地反映岩石流变变形破坏的三阶段，试验曲线与模型拟合曲线的变化趋势一致，从图4(b)、(c)可以看出，在加速流变阶段，试验曲线与模型拟合曲线的总体变化趋势和转折点的数值大小均相吻合，都表现为应变的急剧增大直至岩样破坏，很好地表现了岩石加速流变阶段的非线性，这表明本文所建立的考虑渗压损伤的流变本构模型的合理性和正确性。

3 结论

1)由考虑渗压的二长花岗岩三轴流变试验所得结果，基于广义Bingham模型建立了考虑渗透压力损伤的流变损伤模型，引入损伤变量，考虑了流变过程的非线性建立了损伤演化方程。

2)基于所建立的损伤演化方程建立了改进的广义Bingham模型的流变损伤模型，并对流变损伤模型的力学参数进行了辩识。模型预测结果与试验结果相吻合，显示了该模型的合理性和正确性，该模型可以很好地模拟岩石流变三阶段，且具有参数少，物理意义明确，确定方法简单等优点，具有一定的工程实用价值。

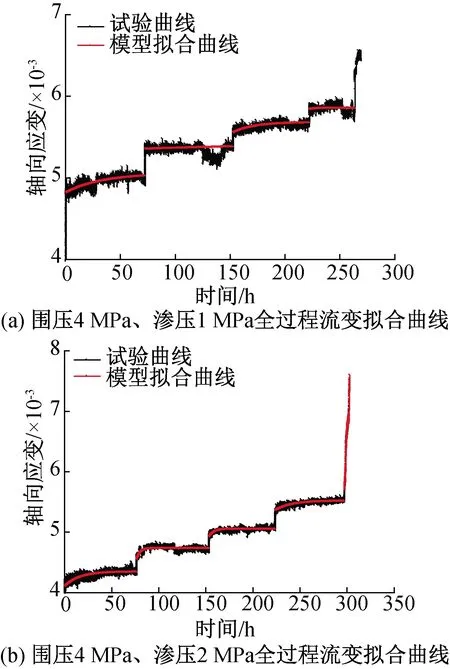
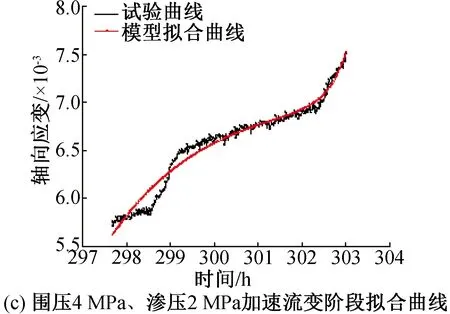
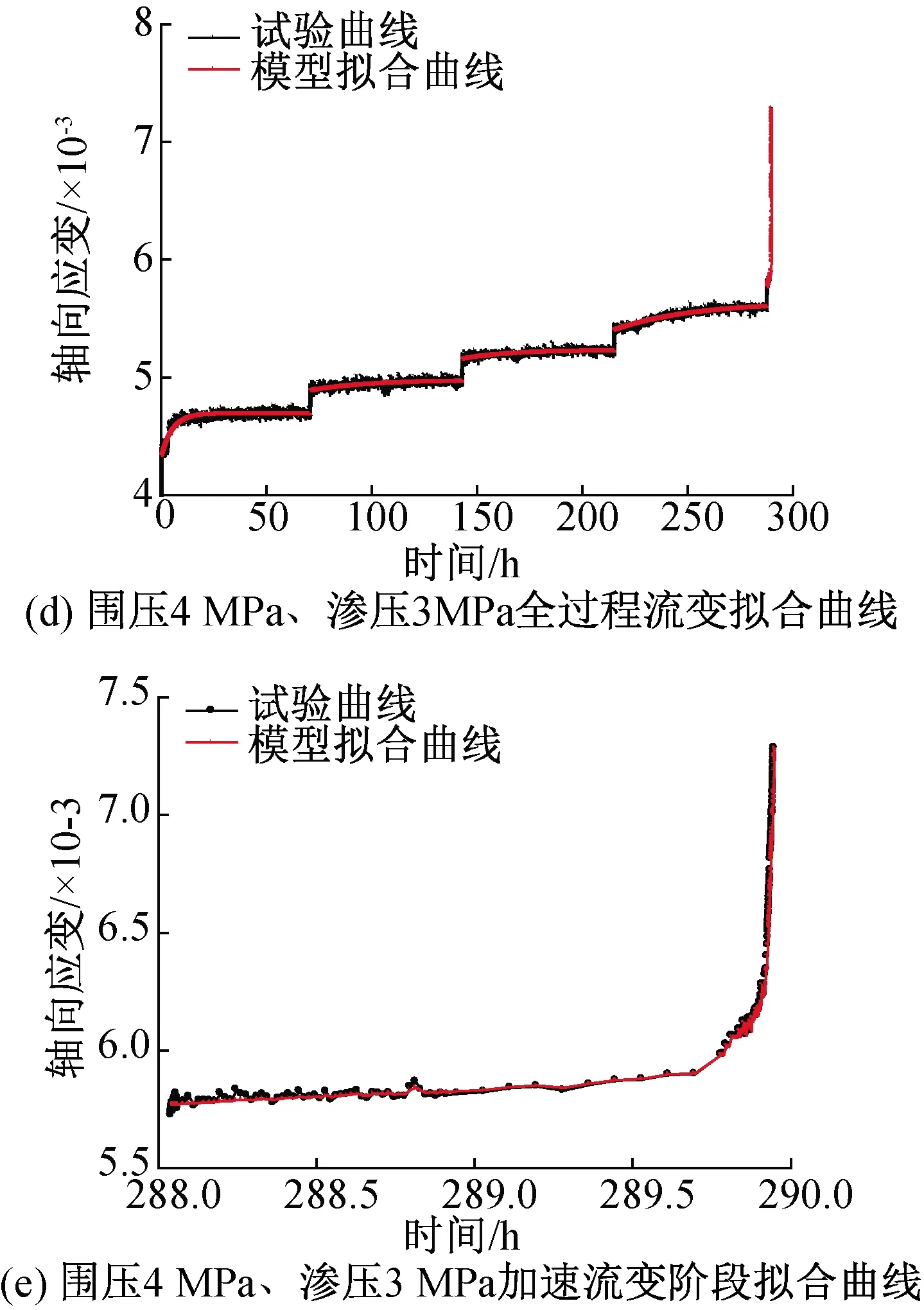
图4 各试验条件下模型拟合曲线与试验曲线对比图Fig.4 model fitting curve and test curve indifferent test condition