基于调制宽带转换器的机械振动信号检测

郭俊锋，刘世润

（兰州理工大学机电工程学院，甘肃 兰州 730050）

1 引言

当机械设备发生故障时一般都伴随着振动的变化，并且通过振动和振动产生的噪声表现出来。通过对这些振动信号进行监测分析可以提前预示和定位故障，以及了解故障原因及恶化程度并及时避免故障的发生。基于振动监测技术设备的故障诊断十分复杂，涉及到多个领域和技术，其中数据采集就是其中的一个关键核心技术。随着机械设备朝智能化、精密化、高速化方向不断发展，机械振动信号的频带也越来越宽，以传统Shannon-Nyquist采样理论对其进行采样将带来海量数据的传输、存储和计算等一系列问题。有时机械设备发生故障所造成的强烈振动冲击中含有的频率很高，需要以极高的速率对其进行采样，现有的模拟/数字转换器（Analog to Digital Convertor，ADC）技术也难以达到如此高的采样速率要求，这样一来就会造成信息的丢失，不能及时的反映出故障，轻则造成机械设备的寿命缩短，重则酿成严重的工程事故。

调制宽带转换器[1-3]是一种利用压缩感知[4-6]（Compressive Sensing，CS）原理对信号进行模拟信息转换（Analog-to-Information Conversion，AIC）[7-9]的采样方案，可以实现对信号的亚奈奎斯特速率采样。同时MWC还具有适用信号类型范围广、计算量小、易于实现、硬件成本低等优点。因此，MWC采样方案一经提出便得到了国内外众多学者的关注和研究。文献[10]提出了一种简单的MWC随机序列生成方法，实现了只需单个移位寄存器通过简单的循环和移位便可产生用于MWC采样系统所有采样通道中进行信号调制的随机序列，仿真实验表明该方法几乎具有最佳的重构性能。文献[11]将MWC采样前端的低通滤波器替换为一个积分器，使得改进后的MWC方案能较好的适用于对高频脉冲信号的采样。针对MWC采样系统在谱带带宽差异较大的情况下存在采样速率冗余的问题，文献[12]提出一种面向信息带宽的频谱感知方法，通过利用谱带宽度先验信息放宽对混频函数频率的限制。文献[13]针对MWC现有重构算法准确重构所需通道数与理论值存在较大差距的问题提出了一种基于奇异值分解（singularvaluedecomposition，SVD）和多重信号分类多信号分类（multiplesignalclassification，MUSIC）的重构算法，实验表明该算法在一定条件下重构所需的最低通道数已接近理论下限值。机械设备结构复杂、工作环境往往比较恶劣，设备工况的改变以及故障的发生等都会使得机械振动信号产生不规律的波动和冲击，因此机械振动信号几乎都属于非平稳信号。从故障诊断的角度来看，一方面非平稳振动信号包含着比平稳振动信号更丰富的信息，可以反映出更多的设备运行状态信息；另一方面非平稳振动信号的采样难度较大，需要对采样系统的采样速率、数据存储传输及信号恢复等问题考虑更加周全才能准确的捕捉到机械设备运行过程中的故障信息。

提出一种基于MWC的机械振动信号采样方法，在不丢失有用信息的前提下实现对机械振动信号的亚奈奎斯特速率采样，重点解决传统采样方法造成的采样数据量大、采样速率高等问题。论文结构安排如下：首先简要分析MWC的工作原理，之后根据测试机械振动信号的先验信息设计合理的MWC采样参数，最后进行实验仿真验证方案的可行性。

2 基于MWC的机械振动信号检测方法

2.1 MWC工作原理

MWC采样系统，如图1所示。输入信号x（t）同时进入m个采样通道，每个通道由一个混频乘法器、一个低通滤波器和一个低速ADC组成。在第i（1≤i≤m）个通道中，信号x（t）首先与周期为Tp混频函数pi（t）相乘进行频谱混叠，目的是将信号的高频部分搬移并叠加到基带频率处；之后，混频信号zi（t）通过截止频率为fp=1/2T的低通滤波器H（t）进行低通滤波得到滤波信号ci（t）；最后ADC以1/T的速率对滤波信号采样得到采样序列yi［n］。由于每个通道的采样率都足够的低，因此现有的ADC设备就可以满足工作需要。

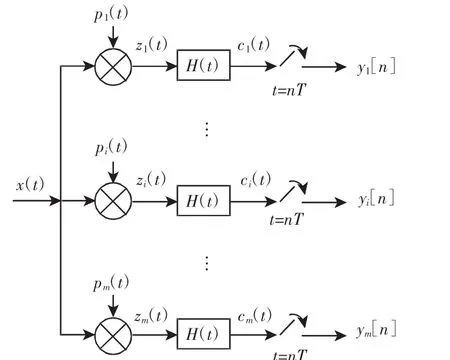
图1 MWC系统方框图Fig.1 A Block Diagram of MWC

系统的设计参数主要有采样通道个数m，采样率1/T，混频函数的周期Tp以及混频函数pi（t）。混频函数pi（t）是一个伪随机周期信号Tp在一个周期内其值变化M次，通常情况下选择取值为±1的m序列作为pi（t）。

下面对MWC的工作原理进行数学分析，定义采样频率区间：

则采样序列yi［n］中只包含位于频率区间Fs上的频谱采样值。因此，采样序列yi［n］的离散时间傅里叶转换（discrete time fourier transform，DTFT）为：

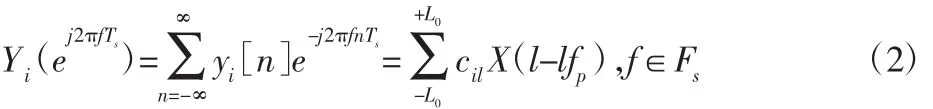
式中：cil—混频函数pi（t）的傅里叶系数；L0—以fp为单位长度将输入信号的最高频率平移L0次后恰好落在频率区间Fs上，但平移L0+1次后便超出Fs，也即：

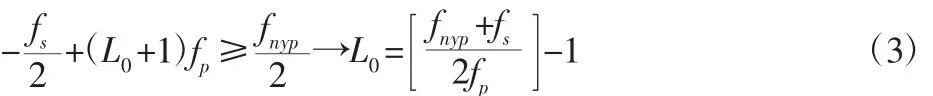
式中：fs（fs=1/T）—ADC的采样频率；［·］—向上取整。方便起见，

将式（4）写作下面的矩阵形式：

式中：y（f）—一个长度为m的向量，第i项yi（f）=Yi（ej2πfTs），1≤i≤m；矩阵 A 由傅里叶系数 cil构成，且有 Ail=ci，-l；z（f）是一个长度为L=2L0+1的向量，其第i项为zi（f）=X（f+（i-L0-1）fp），1≤i≤L。

2.2 信号恢复

从采样序列yi［n］中恢复信号x（t）的关键在于找到信号的支撑集S，也即向量z（f）中非零位置的索引值，其定义为：

令矩阵AS为矩阵A由支撑集S索引的列向量构成的子矩阵，向量zs（f）为向量z（f）中由S索引的项，一旦得到支撑集S，则有：

由于f在区间Fs上连续取值，因此线性方程（5）是无限测量向量（Infinite Measurement Vectors，IMV）系统，求解支撑集S需要进行无限多次迭代属于NP-hard问题。针对此问题，文献[1]提出一种连续-有限（Continuous to Finite，CTF）的方法，该方法首先将无限测量向量问题转换为多重测量向量（MultipleMeasurementVectors，MMV）问题，然后运用压缩感知相关重构算法求解支撑集，CTF流程，如图2所示。

图2 CTF原理框图Fig.2 The Schematic Diagram of Continuous to Finite（CTF）

支撑集记录S的是稀疏解U0中非零元素所在位置的索引值，如图2所示。有限维框架V通过下式进行构造：

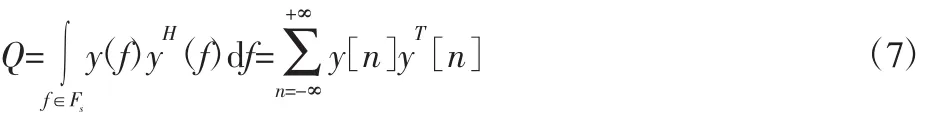
y［n］=［y1［n］，…，yk［k］］T表示在时刻 nT 的观测数据，任何满足Q=VVH的矩阵V都可作为观测向量y（f）的一个有限维框架。获得框架V之后求解线性方程V=AU属于MMV问题，可用压缩感知中的同步正交匹配追踪算法（Simultaneous Orthogonal Matching Pursuit，SOMP）来求解支撑集 S。

2.3 振动信号的检测方法

基于MWC的机械振动信号检测方法实现步骤如下：

（1）从美国凯斯西储大学轴承数据库中提取振动数据；

（2）在时域和频域中对轴承振动信号进行观察，得到实验信号的先验信息；

（3）根据实验信号的先验信息及频谱划分方式设计合理的MWC采样系统参数；

（4）MWC对输入信号采样得到观测数据；

（5）使用CS重构算法完成信号恢复；

（6）调整MWC的相关参数和信号划分谱带的带宽，重复步骤（2～6）。

基于MWC的机械振动信号检测方法流程图，如图3所示。

图3 基于MWC的机械振动信号检测方法流程图Fig.3 The Flow Chart of Signal Detection of Mechanical Vibration Based on MWC

下面根据实验所选机械振动信号设计合理的MWC采样系统进行信号仿真实验，实验信号选用美国凯斯西储大学（CWRU）轴承研究中心的轴承数据，轴承型号为6205-2RS JEM SKF，轴承类型为深沟球轴承，转速为1797r/min，采样频率为48KHz，电机无加载负荷。轴承故障点采用电火花方式加工生成，故障点位于轴承外圈6点钟方向，大小为0.021″。根据CWRU提供的资料，外圈发生故障时其故障频率为：

式中：fr=29.95Hz—轴承转频。实验信号的时域波形图及细节图，如图 4（a）、图 4（b）所示。

从轴承振动信号时域波形细节图中可以看出故障点的振动通过周期冲击波形表现，并且在轴承再一次经过故障点之前迅速衰减。图4（c）所示分别是实验信号的频谱图，由于轴承振动信号为实信号，因此其频谱图呈对称形状；从图4（c）中可以看出，信号的能量主要集中在（0～4）kHz的频率区间，在此区间之外的频率幅值接近于零。在（0～4）kHz的频率区间内可以根据信号能量集中程度对频谱进行划分，划分区间的宽度决定了信号频谱所包含的子带个数及子带带宽，并直接影响着MWC系统的参数设计。MWC采样系统实现所需要的硬件，包括混频器、低通滤波器、模拟-数字采样器等与采样通道的个数成正比，因此，减少通道个数可以降低硬件实现的成本。轴承振动信号频谱细节图，如图4（d）所示。选取了图 4（c）左半部分对称频谱中（0～4）kHz的频谱。

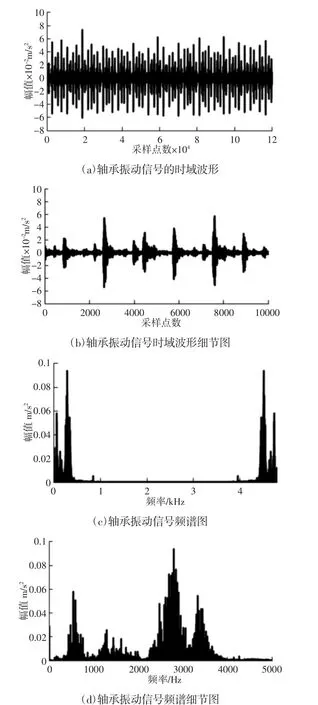
图4 轴承振动信号时域波形及频谱图Fig.4 Time Domain Waveform and Spectrum Diagram of Bearing Vibration Signal

轴承外圈发生故障时的频谱成分较为简单，主频为故障频率，实验信号包络谱，如图5所示。从图中可以看出其频谱主要由轴承转频 fr、故障频率 fo及其谐波 2fo、3fo、4fo等成分组成，若实验中MWC采样系统重构信号的包络谱中含有fo及其谐波成分，则可认为轴承有故障频率为fo的外环故障。

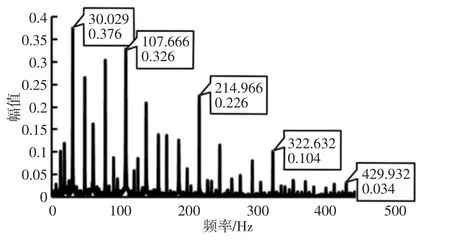
图5 轴承振动信号包络谱Fig.5 The Envelope Spectrum of Bearing Vibration Signal

在MWC采样中，采样通道个数的减少是以提高MWC采样系统的总体采样率为代价的，因此有必要对不同的频谱划分区间大小进行对比，确定最优设计参数。轴承振动信号频谱的两种划分方式，如图6所示。在（0～4k）Hz的频率区间内划分出了2 个子带，子带的最大带宽 2kHz，如图 6（a）所示。将（0～4）kHz的频率区间细划分为4个子带，子带的最大带宽为1kHz，如图6（b）所示。

调制宽带转换器的参数：由轴承振动信号频谱的对称性可知实验信号谱带个数为（0～4）kHz的频率区间内划分谱带个数的两倍。若划分谱带的最大带宽为Bmax，则实验信号的频谱可以划分为L=fnva/Bmax个宽度为Bmax的谱带。为了避免边沿效应，L的取值应略小于计算值；为保证准确重构原始信号，采样通道个数取为子带个数的4倍，表1所示是两种频谱划分方式下的MWC采样系统设计参数。

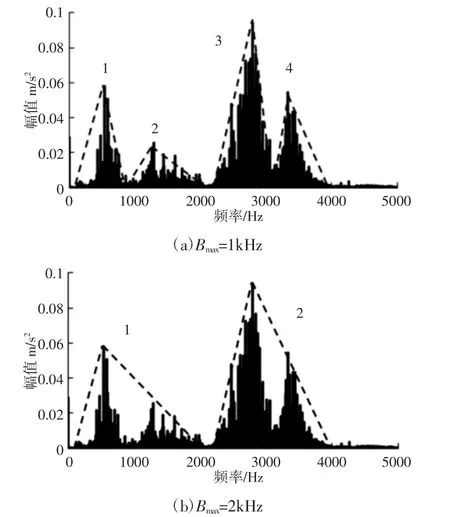
图6 轴承振动信号频谱的两种划分方式Fig.6 Two Kinds of Division Methods of Bearing Vibration Signal Spectrum

表1 两种频谱划分方式下的MWC参数Tab.1 The Parameter of MWC Under Two Kinds of Spectrum Division Methods

从表1可以看出，采样通道数随着谱带个数的增加成比例增大，但是MWC系统的总体采样率fΣ却在减少。在单个通道ADC的采样率方面，当子带个数等于4时对应的采样率fs是子带个数等于8的一倍多，因此频谱划分的越细ADC的采样速率越低；当轴承振动信号谱带个数分别为N=4和N=8时，MWC采样系统总体采样速率对比于实验信号的奈奎斯特速率分别降低了30.33%和32%。

2.4 重构效果

根据表2计算的参数设计合理的MWC采样系统对轴承振动信号进行低速采样并进行信号重构，重构信号的包络谱，如图6所示。

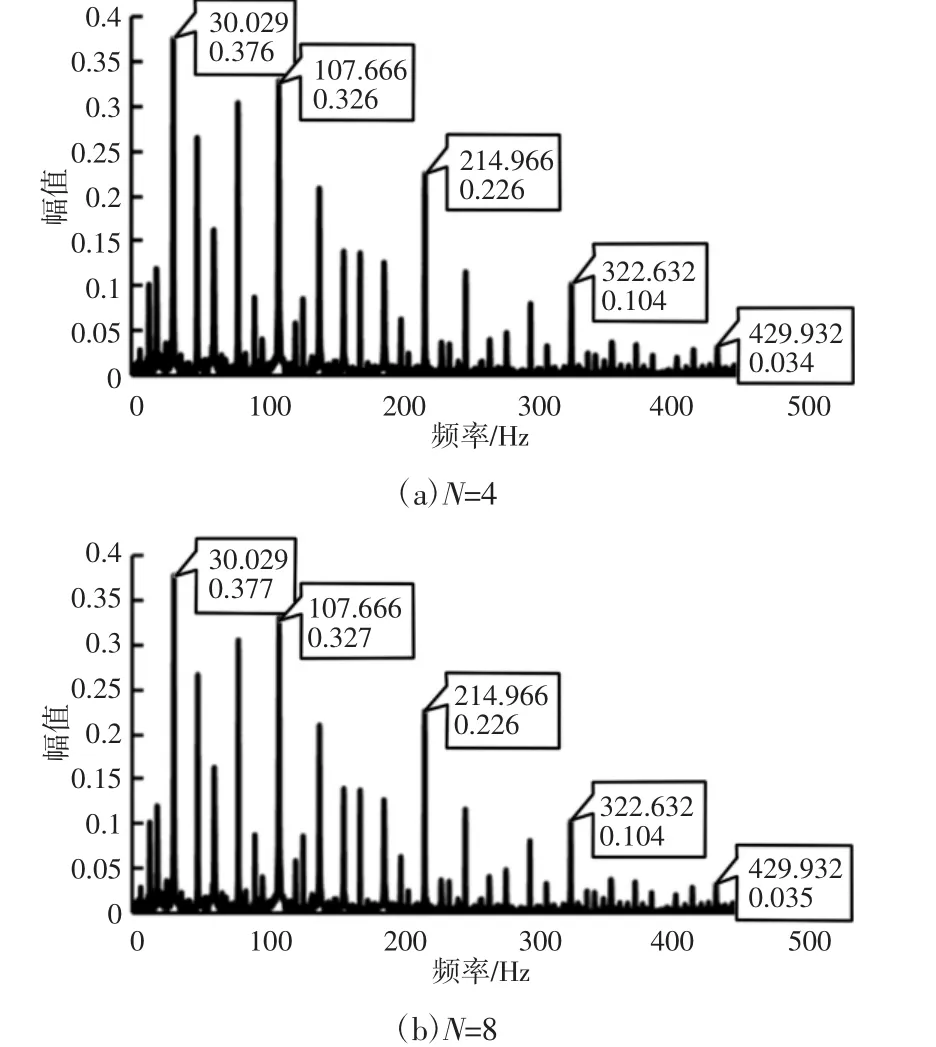
图7 两种频谱划分方式下MWC重构信号效果Fig.7 Reconstruction Performance of MWC Under Two Kinds of Spectrum Division Methods

原始轴承信号包络谱图5和重构信号包络谱图对比可以看出，重构信号包络谱除了在幅值方面与原始信号包络谱有稍微的误差，其精确的重构出了原始信号的转频、故障频率及其谐波成分。

2.5 信号频谱划分方式和MWC采样通道数对信号重构的影响

为了进一步验证所述方法的性能，下面进行两组实验研究不同频谱划分方式和采样通道个数与重构误差之间的关系。重构误差按均方误差计算，定义如下：

式中：x—原始信号；xrec—重构信号。

2.5.1 MWC采样通道数对信号重构的影响

本次实验在前文实验基础上分析了采样通道数与重构误差之间的关系，实验中m的取值范围为（2～8）N，针对每个m取值进行100次重构实验，误差取平均值。子带个数分别取N=4和N=8时，如图8所示。采样通道数与重构误差之间的关系。

图8 谱带宽度不同，采样通道数与重构误差的关系Fig.8 The Relationship of Sampling Channels and Reconstruction Error Under Different Spectrum Bandwidth

由图8的实验结果可以看出，当采样通道数m在（2～4）N范围取值时，信号重构误差随着采样通道数的增加迅速降低，并且当m=2N时，谱带数N=4对应的重构误差要远远大于谱带数N=8；当采样通道数m≥4N时，信号重构误差逐渐趋于平稳；在实际信号采样中，采样通道数的选择应在信号重构精度和采样系统硬件成本之间权衡，采样通道数取值较小时信号重构误差较大、重构效果差；取值较大时尽管信号重构稳定、重构误差小，但是大大增加了MWC硬件实现的成本。因此，采样通道个数的选取只需保证能够准重构出原始信号的故障频率即可。

2.5.2 信号频谱划分方式对信号重构的影响

由表1的结果可知划分谱带的宽度对MWC采样系统的采样速率有较大影响，本次实验在（0～4）kHz信号能量较为集中的频率区间上分别以 2kHz、1kHz、500Hz、250Hz、100Hz、50Hz划分宽度对轴承振动信号的频谱进行细化，对应的谱带个数分别为2、4、8、16、32、80、160。实验中针对不同的谱带数进行 100 次重构实验，误差取平均值，测试结果，如表2所示。

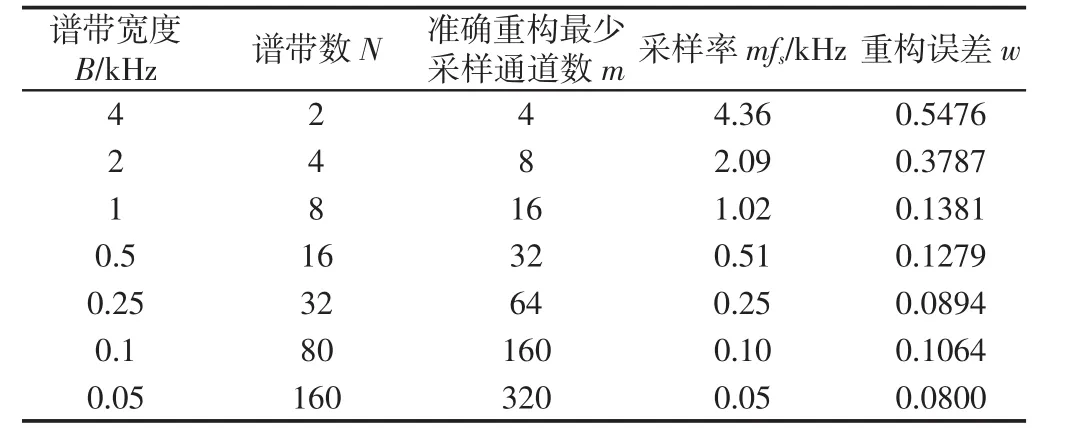
表2 不同谱带宽度下的MWC重构效果Tab.2 Reconstruction Performance of MWC Under Different Spectrum Bandwidth

从表2的实验结果可以看出，MWC采样系统的总体采样率和重构误差随着划分谱带带宽的减小而降低，但是准确重构所需的最少采样通道数却成比例增加。因此，频谱划分的越细，采样系统硬件成本越高。在实际采样中，应根据信号重构精度要求和硬件成本合理的划分谱带宽度从而达到理想的采样效果。

3 结论

传统的Shannon-Nyquist采样方法对轴承信号进行采样造成了海量数据的传输、存储和计算等一系列问题，有时轴承发生故障所造成的强烈振动冲击中含有的频率很高，进行采样的奈奎斯特频率已经超出了现有采样设备所能达到的最高频率，这样一来就会造成信息的丢失。调制宽带转换器采样系统突破了奈奎斯特采样速率的约束，以远低于奈奎斯特速率对信号进行采样，并能准确重构出原始信号。将调制宽带转换器采样系统应用于轴承振动信号的采样，在不丢失振动信号信息的情况下，大大减少了采样数据量。从重构信号包络谱来看，其准确的恢复出了原始信号的故障频率信息，对轴承故障信息的预测提供了有力的保障。