基于含石量差异的土石复合体边坡稳定性及失稳机制分析

摘要：文章借助FLAC数值模拟系统，将土石复合体视为一种二元物材料，以数理模拟计算的方式，对含石量差异下的土石复合体边坡稳定性及失稳机制问题进行分析，以为同类工程应用提供研究和技术参考，助力建设安全牢固的土石复合体边坡工程。

关键词：土石边坡;复合体;含石量;稳定性;失稳机制;分析探究

0 引言

在工程中，通常将土石复合体看作是一种特殊的均质土体进行处理，也会将其看作是不可分割的整体进行处理，由此便可直接确定出其整体抗剪强度参数c和φ。在对玛河流域内土石复合体边坡的现场情况进行实地考察与深入研究后发现，该地区的块石不仅分布差异大，而且构成量不均。如果将该边坡计算模型设定为单一地质体构造，并将土石复合体看作是一种不间断均质地质材料，由此生成的计算结果与其他性质的边坡大体相同，但与现实情况却存在很大不同。故在本研究中，笔者将土石复合体视为一种二元物材料进行数值模拟分析，也就是说，边坡构造比较简单，只由黏土和块石构成。具体来讲，先根据块石构成量建立相匹配的边坡模型，再将黏性土视为基质，无规律地分布块石。

1 模拟土石复合体边坡方法简述

无论哪种性质的材料，一般的计算方法都根据勘察材料对边坡进行地层划分，还会将各地层全部看作是均质体。不过，由于土石复合体边坡与常规边坡不同，倘若也将其看作均匀地质体，则很难达到预期的优化效果，因此需将其看作是一种“二元物”材料，即只由黏土和块石组成的一种简单构造。由于块石有大有小，分布过于散乱，不仅增强了土石复合体的力学复杂性，还形成了不同寻常的损坏模式。本文旨在从源头上探讨土石复合体边坡的稳态性和失稳机制，引入了功能强大、操作便捷的FLAC模拟系统，期望能获得更客观、更真实的数据结果。

1.1 FLAC简介

FLAC数值模拟系统是当前颇受业界人士推崇与青睐的一款专业分析软件，它由国外知名企业Itasca自主研发，现已凭借操作便捷、功能强大、精准可靠等优势在支护设计、矿山工程等众多领域实现了规模化普及与广泛应用。由于FLAC在模拟地质材料方面具有无与伦比的优势，无需过多计算便能推导出边坡的安全常数，确定出剪应变带及弹塑区，因此成为岩土工程领域研究的常用软件之一。另外，FLAC内置主流编程语言FISH，用户可根据自身需求设计相应的程序语句，以确保FLAC的功能优势被全面发挥。在本课题研究中，笔者利用强大的FISH语言编写算法语句并对土石复合体中的土石构造进行直接模拟，而这些操作可完全通过FLAC软件完成，用户不用另行外接编码程序。值得一提的是，本方法支持用户对各项参数的自行设定，比如模型规格、单位长度和块石构成量等。

1.2 模拟土石复合体边坡的模型实现方法

在本研究中，可将土石复合体看作是只由块石和土体构成的“二元物”构造。为简化模拟程序、减少计算量，需借助FLAC中的网络单元对土体和块石的属性进行赋值。但在实际操作中，需注意以下几点：（1）如何实现块石离散、随机分布，以尽可能地贴合实际情况，并非人为地分布块石;（2）如何合理确定含石量。实际上，利用FISH语言编程就能妥善解决上述问题。

在FLAC模拟分析软件中，可通过坐标（i，j）对网络部位进行标记，为保证块石随机分布，可通过自行编制的FISH语言生成随机实数对（i，j）来实现，i及j指的是网络的横、纵坐标。由此便可通过科学定位的方式随机分布块石，通过网络数目定义含石量。

2 土石复合体边坡数理模型

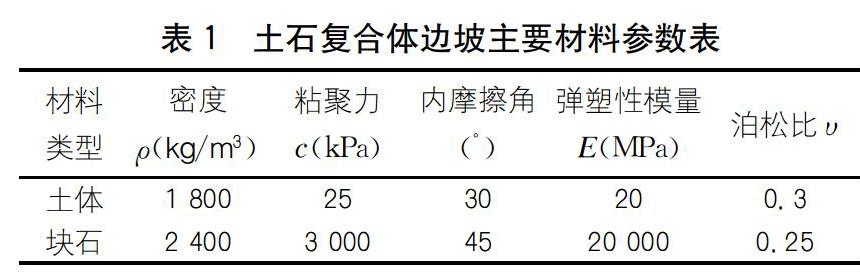
由于在本研究中只涵盖了土体和块石这两种简单的地质材料，为深入探讨与全面研究边坡稳态性，要先确定出这两种材料的物理力学参数值。笔者根据文献，利用Mohr-Coulomb模型确定了这两种材料物理力学参数的具体值，见表1。

通过细致观察可以发现，边坡模型规格与前文反演计算边坡模型无任何差异。为精准确定出不同含石量对边坡稳态性和失稳机制造成的影响，笔者先对均质土质边坡进行了有效计算，也就是对含石量为0的边坡稳态性进行了勘察计算，并将由此生成的结果作为参照。边坡计算模型网络边长度为0.33 m，由于土石复合体中>0.33 m的块石构成量低于50%，所以笔者只对含石量≤50%的边坡稳态性进行研究。

通过图1可对不同含石量的边坡稳态性有更直观的了解与认知。其中，土体用黑色块描述，块石用白点描述。在含石量相同但块石分布不同的情况下，通过本方法也能构建出相匹配的边坡模型，从而也就能探讨出块石分布与边坡稳态性之间的关系。

3.1 边坡的稳定性和失稳路径分析

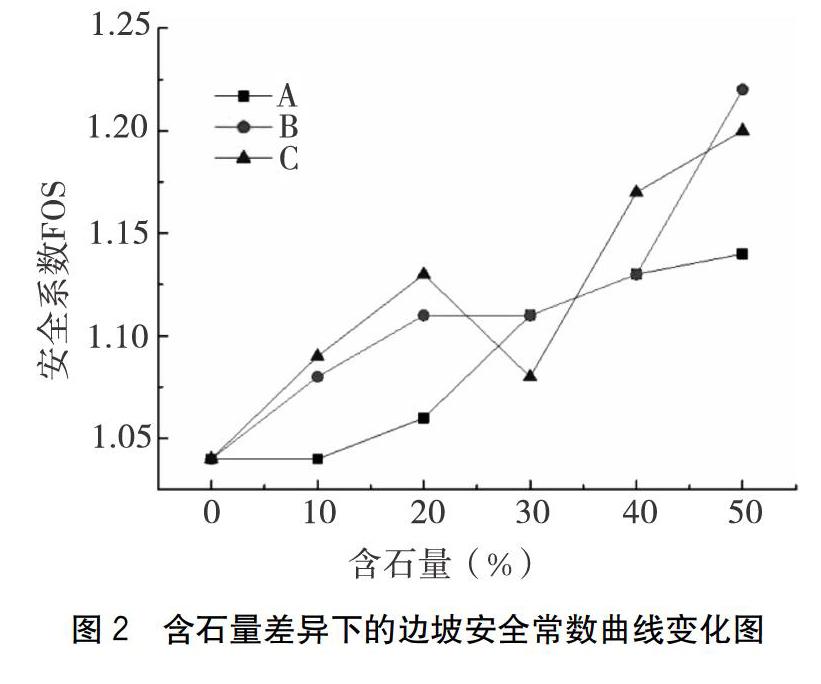
通过图2可对含石量差异下边坡的安全常数演变曲线有更直观的了解与认知。为了实施比对分析，笔者专门设置了A、B、C这3组，以探讨出块石分布不同但含石量递增使土石复合体边坡稳定性发生变化的情况。但因为篇幅较短，只构建了A组含石量为0～50%块石分布边坡模型。通过图2数据分析发现，在含石量为0的情况下，边坡的安全常数为1.04。在含石量不断增大的情况下，边坡的安全常数也表现出明显的递增趋势。很明显，这与宏观认知是完全相同的，也就是说块石的含石量与土质边坡的力学机能变化存在直接联系，不过因为每组边坡的块石分布不同，即便含石量不断增大，边坡的安全常数走势也会出现明显差异。在含石量不断增大的情况下，B组的安全常数迅速升到了1.22，而A仅为1.14。但C组却出现了截然不同的情况，虽然含石量持续增加，不过安全常数却一直走低，说明这与土体本身的特性存在密切关联。在FLAC模拟系统中，利用强度折减法对边坡稳态性进行计算，同时将有无弹塑区贯通或计算不收敛作为失稳判定依据。由于土体构成量随着块石构成量的不断增大而持续走低，而且低强度土体容易形成弹塑区，所以含石量增大会加大弹塑区贯通难度，从而也就能有效强化边坡稳态性。不过因为块石是随机分布，一旦过度集中于坡体上部，必然会加大下滑力，反倒更容易使彈塑区贯通，也就无法保证边坡的稳定性。当含石量为30%及40%时，B、C两组的安全常数一致，这表明在块石分布不同的条件下，边坡的整体稳态性也能相统一，但并不意味着边坡的失稳机制是完全一致的。[FL）]

通过图3可对含石量为0～50%的边坡滑移带的演变情况有更直观的认知与了解。边坡的滑移带在含石量为0也就是说边坡为均质土质构造的情况下，呈不规则形状，边坡中部和底部形成了最大切剪应变力，滑移带整体呈弧线形。边坡的最大切剪应变率因含石量持续增大而相应减低，由此表明，块石的嵌入能对边坡的力学机能起到良好的改善作用，还能从整体上强化边坡抗剪力。相较于均质土质边坡，土石复合体边坡的滑移带则因含石量增加而呈现凹凸不平的形状，不仅宽度会相应增加，发生数个分支，还容易出现裂断，此种态势会因含石量不断增加而愈加明显，最终致使滑移带形成不规则形状，即失稳路径愈加不明显。尽管在含石量很少时，均质土质和复合体这两种边坡的差距不太明显，但都不能呈规则形状，而且表面凹凸更为显著，其原因是块石使均质边坡力学特性发生了变化，而且滑移带绕过了大抗剪强度的块石。通过实验数据分析发现，切剪应变力不再聚集于边坡上部，而是转移到了边坡中部及下部。

边坡滑移带形状因含石量的不断加大而愈发不规则，而且局部切剪应变较大区域聚集了不断增大的应变力，致使边坡整体不再呈条带状，边坡的中下部不仅是应力集中区，还是易失稳损坏区。在失稳的过程中，由于抗剪强度参数持续减低，就容易在强度小的土体区域发生屈服，而边坡中块石仍处在弹塑性状态，因此滑移带通常绕过边坡中的块石，形成特有的“绕石”现象，恰恰这是导致滑移带不规则且呈“聚团”状的真正原因。与室内三轴实验等不同，因为边坡未形成较大的剪应力，因此在失稳损坏期间，块石很难破碎，“绕石”现象也就愈发突出。滑移带形状不规则的另一原因是块石聚团，由于块石的影响，滑移带呈裂断状，而无法形成真正意义上的连通区域，此种表现在含石量为50%时更为严重，滑移带不仅无序还不规则，不仅呈明显“聚团”状，也存在多分支构造发生，甚至局部切剪带延伸到坡面呈一定角度与坡面相交。

3.2 边坡失稳机制的数理分析

通过图4可对含石量为0～50%的边坡弹塑区的演变情况有更直观的认知与了解。承拉屈服区域在含石量为0时主要分布在坡顶中部，受剪屈服区域则从坡顶一直贯通到底部，由此构成一条完整、规则且呈流畅弧线形的弹塑区贯通带。在含石量不断加增的情况下，承拉屈服区域主要出现在边坡顶部，但分布不均匀，关键是此种现象会因含石量越大而愈加严重。但受剪屈服区域却演变成为不规则形状，并与承拉屈服区域盘根交叉。

在含石量控制在10%～20%的情况下，受剪屈服区域演变与滑移带比较相近，但由于块石的存在，受剪屈服区域呈不规则条带状。受剪屈服区域与承拉屈服区域互相交错形成弹塑区贯通带，顶部出现较为明显的承拉损坏，而中部及底部则表现为受剪损坏，特别是滑移带上部岩土体失稳最严重，但滑体整体性能表现为良好。

在含石量达到30%～50%的情况下，边坡内部受剪屈服区域会发生明显移位，整体演变趋势为：边坡内部→坡面附近→坡体内部，受剪屈服区域呈不规则形状，并与承拉屈服区域盘根交错。承拉屈服区域主要分布在边坡顶部，距离坡面非常近，通过交错受剪屈服区域构成弹塑性贯通带。因为受剪屈服区域分布在中下坡的表面，并与承拉屈服区域盘根交错，一旦下部坡体失稳必然会引发垮塌式散体状损坏，其原因是块石及土体力学特性差异过大。具体来讲，在含石量持续增大的情况下，当边坡发生损坏时，块石及土体触接面容易受剪或者承拉屈服，也就容易形成散体状损坏。再加上在边坡顶部形成了拉应力带，在下部稳定性能丧失后，顶部岩土体就会迅速形成拉裂带，部分土石复合体缓慢坠落，从而构成下部垮塌-上部拉裂滑坡。此种表现在含石量为50%时尤为严重。另外，受剪屈服区域与承拉屈服区域互相交错，会加大屈服岩土体深度，也就不能形成独立的屈服带，则会演变成为块状弹塑性屈服区域。

4 结语

本研究以数理模拟计算的方式，对含石量差异下的土石复合体边坡稳定性及失稳机制问题开展专题分析探究。主要收获为：（1）介绍了将土石复合体视为一种二元物材料的土石复合体边坡模拟方法;（2）基于二元物材料设定建立了土石复合体边坡数理模型;（3）基于含石量差异，对土石复合体边坡稳定性和失稳机制开展了数值计算和机制分析，边坡稳定性和失稳路径分析揭示：块石的含石量与土质边坡的力学机能变化存在直接联系，低强度土体容易形成弹塑区，高含石量则会加大弹塑区贯通难度，块石过度集中于坡体上部，会加大下滑力，增大弹塑区贯通发生概率，威胁边坡稳定性;（4）边坡失稳机制的数理分析揭示，含石量控制在10%～20%的情况下，受剪屈服区域演变与滑移带比较相近，在含石量达到30%～50%的情况下，边坡内部受剪屈服区域会发生明显移位，趋势为：边坡内部→坡面附近→坡体内部，受剪屈服区域呈不规则形状，并与承拉屈服区域盘根交错。

参考文献：

[1]张 群.基于细观机制的土石混合体边坡稳定性研究[D].武汉：长江科学院，2012.

[2]张东亮.地震作用下土石混合体边坡稳定性研究[D].成都：西华大学，2010.

[3]葛华康.高含石量土石混合体高填方边坡稳定性与变形研究[D].重庆：重庆大学，2016.

[4]徐鼎平.基于三维数值模拟的边坡稳定性分析的整合方法研究[D].马鞍山：马鞍山矿山研究院，2007.

[5]黃献文.动荷载作用下土石混合体变形特性及边坡响应规律研究[D].镇江：江苏科技大学，2019.

作者简介：蒙培峰（1988—），工程师，从事公路桥梁勘察设计工作。