岩溶区土洞基础稳定性解析研究

赵明华，肖 尧，赵 衡，徐卓君,胡 倩

(湖南大学 岩土工程研究所，湖南 长沙 410082)

0 引言

我国疆域辽阔，地质条件复杂，岩溶就是工程中常见的不良地质，其主要分布在我国西南地区[1]。岩溶区常见的产物有土洞和溶洞，空洞的存在极大的削弱了基础承载力，其稳定性分析关系到工程的安全性[2]。因此，对岩溶区土洞基础稳定性分析具有重要的工程实践价值。

目前，国内外许多学者已经对空洞的稳定性问题进行了研究，分析方法主要有模型试验、数值分析和理论计算。考虑轴对称模型，Baus 和Wang[3]基于室内模型试验，对条形基础荷载作用下硬黏土中的空洞稳定性进行了研究。随后，Badie和Wang[4]通过模型试验探讨了土洞与基础偏移位置对承载力的影响。采用离心机试验,Kiyosumi等[5]对条形基础荷载作用下多个空洞的稳定性进行了分析。模型试验能有效地探讨机理方面的问题，但造价昂贵，对于更多影响因素的探讨可采用数值分析作为补充。Kiyosumi等[6]采用有限元法对多空洞地层上条形基础的屈服荷载进行了计算。在此基础上，Lee等[7-8]对不排水条件下土洞的稳定性进行了研究，并探讨了倾斜荷载的影响。Xiao等[9-10]采用有限元极限分析法对条形基础荷载作用下双层土和岩体中的多空洞稳定性进行了研究。理论研究方面，Wang和Hsieh等[11]对、刘辉等[12]考虑轴对称模型，采用极限分析上限法对条形基础荷载作用下土洞的稳定性进行了分析。刘之葵等[13]基于弹性理论，求得条形基础荷载作用下土洞周边土体的应力状态，并采用Mohr-Coulomb屈服准则，对土洞稳定性进行了评价。赵明华等[14-15]、胡柏学等[16]和雷勇等[17]对岩溶区桩基承载性能进行了研究，得到了相应的计算公式。李倩倩等[18]和赵衡等[19]采用复变函数的方法分别得到了椭圆形、矩形空洞地层应力场的精确解答，并对空洞的稳定性进行了分析。以上理论分析对基础荷载作用下土洞的稳定性进行了深入的探讨，但仍存在以下不足：其一，以上理论分析方法不能考虑非均布荷载对土洞稳定性的影响；其二，现有分析计算方法均采用轴对称计算模型，其不适用于非对称条件下土洞稳定性的评价。

鉴于此，首先根据工程实际情况简化得到8种不同的计算模型；其次，基于Boussinesq解、Mindlin解分别对地层表面基础荷载、地层内部基础荷载进行积分，得到非均布基础荷载作用下半无限空间内任意点的应力状态；然后，基于复变函数理论，求得圆形、椭圆形土洞在自重作用下的应力，同时得到考虑地下水影响的应力表达式；最后，将基础荷载作用下的应力状态与土洞在自重作用下(考虑或不考虑地下水)的应力状态进行叠加，并引入Mohr-Coulomb屈服准则，对土洞稳定性进行评价。该方法能综合考虑基础荷载的非均布及非对称性，对岩溶区土洞基础的初步设计具有较强应用价值。

1 计算模型

根据工程实际合理简化得到如图1所示的8种不同工况条件下的计算模型，并假定：

(1)地层中土洞为深埋空洞，截面形状简化为圆形或椭圆形；

(2)土洞纵向无限长，视为平面应变问题；

(3)地层中土体为理想弹性均质材料。

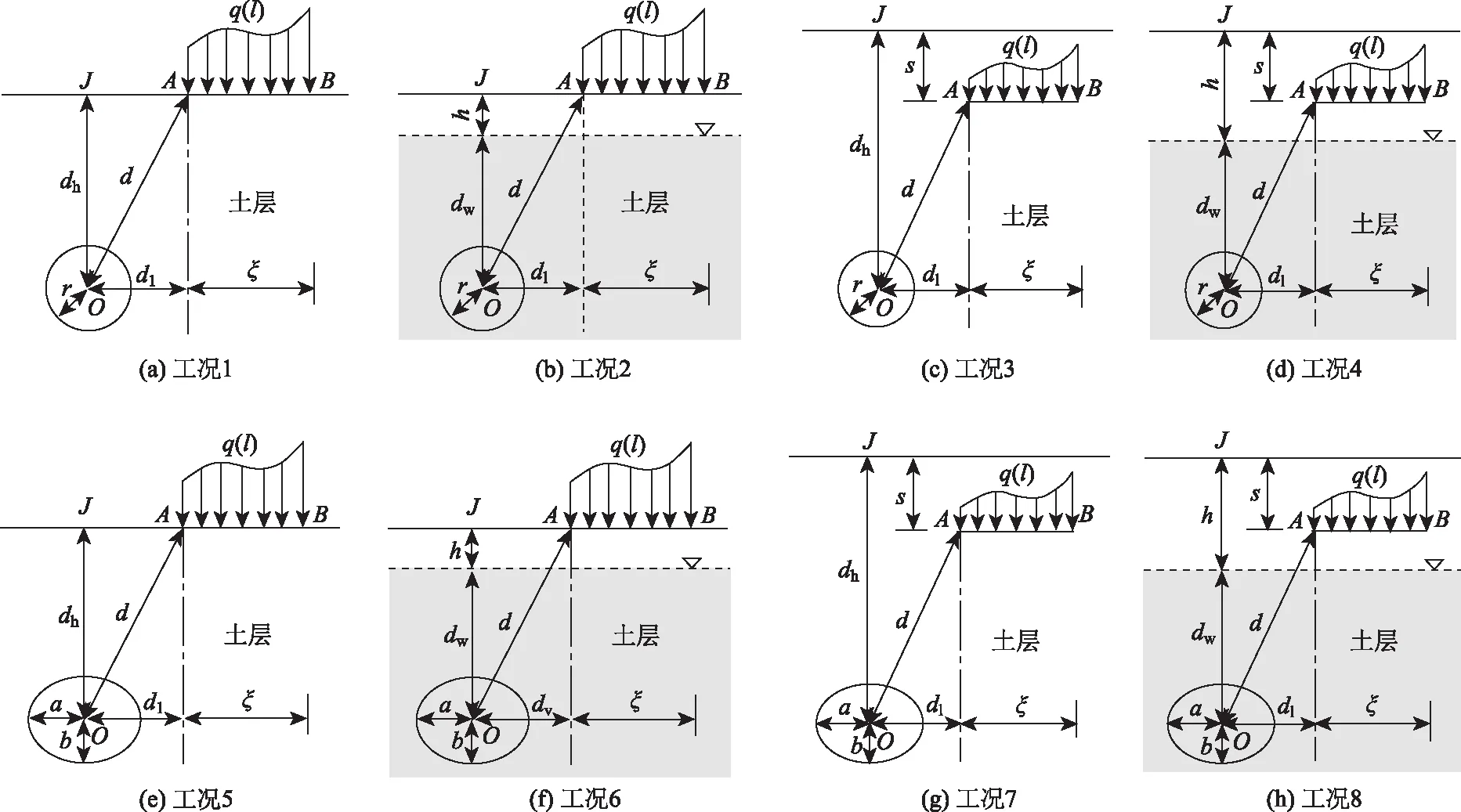
图1 假定计算模型Fig.1 Assumed calculation model

图1中A和B为基础荷载的两个端点；O为圆形、椭圆形土洞几何中点；J为通过O点的垂线与土层表面的交点；d、dl分别为O点与A点的直线距离、水平距离；dh为土洞中心点O到土层表面的垂直距离；dw为土洞中心点O到地下水表面的垂直距离；ξ为基础的宽度；s为基础的埋置深度；h为地下水表面到土层表面的距离；r为圆形土洞的半径；a、b为椭圆形土洞的长轴、短轴；q(l)为基础荷载。

2 土洞稳定性分析

2.1 基础荷载作用下地层应力求解

由图1可知，基础荷载作用于地层表面或地层内部，下面将分别对两种不同基础荷载作用下的地层应力进行求解。

(1)基础荷载作用于地层表面

图2 坐标系L1，L2Fig.2 Coordinate systems L1 and L2

图1(a)、(b)、(e)、(f)为基础荷载作用于地层表面的情况，以J点为原点，地层表面为x轴，OJ为z轴，建立直角坐标系L1,见图2(a)。

在Boussinesq解的基础上，对q(l)进行积分，可得到基础荷载作用下任意一点M(x,z)的应力，表达式如式(1)～(3)所示：

(1)

(2)

(3)

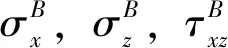
(2)基础荷载作用于地层内部

图1(c)、(d)、(g)、(h)为基础荷载作用于地层内部的情况，以J点为原点，地层表面为x轴，OJ为z轴，建立如图2(b)所示的直角坐标系L2。

在Mindlin解[20]的基础上，对q(l)进行积分，可得到基础荷载作用下任意一点M(x,z)的应力，表达式如式(4)～(6)所示：

(4)

(5)

(6)

(7)

2.2 土洞在自重作用下应力求解

本研究的对象主要包括圆形土洞、椭圆形土洞，下面将分别给出圆形、椭圆形土洞在自重作用下及含地下水时应力场的求解，具体内容和过程如下：

(1)土洞为圆形时

图1(a)～(d)为圆形土洞的情况，不考虑地下水时，圆形土洞受力分析如图3(a)所示，并取直角坐标系K1。

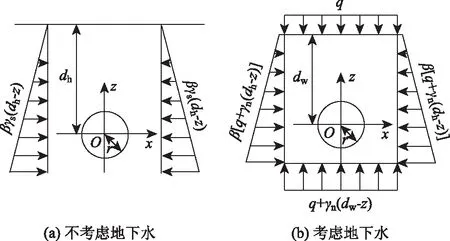
图3 圆形土洞受力分析Fig.3 Force analysis on circular soil cave

图3中，γs和γn分别为土体的重度、浮重度；q为地下水表面以上土层的荷载；β为地层侧压力系数，可由式(7)求得。

β=ν/(1-ν)。

(8)

文献[21]采用复变函数的方法，对该问题进行了求解。

取映射函数：

Ζ=ω(ζ)=rζ。

(9)

解得不考虑地下水时，圆形土洞在重力作用下的应力表达式，如式(10)～(12)所示。

σθ=-0.5μ1μ2(1+α2)+0.5μ3[α+0.5μ4ρ+

0.5μ2α3-μ5(α3+α)]sinθ-0.5μ1μ6(1+3α4)·

cos 2θ+μ3μ6(α5-0.25α3+0.25ρ)sin 3θ， (10)

σρ=0.5μ1μ2(α2-1)-μ1μ6(2α2-0.5+1.5α4)·

cos 2θ-μ3μ6(α5-1.25α3+0.25ρ)sin 3θ-0.5μ3·

[α+μ5(α-α3)+0.5μ2α3-0.5μ7ρ]sinθ，

(11)

τρθ=μ3(0.25μ2α3+0.25μ6ρ-μ8α-0.5μ5)·

cosθ-μ1μ6(0.5-1.5α4+α2)sin 2θ+

μ3μ6(-0.25ρ-α5-0.75α3)cos 3θ，

(12)

式中，σθ，σρ分别为曲线坐标下θ，ρ方向上的正应力；τρθ为切应力；μ1=γsdh；μ2=1/(1-ν)；μ3=γsr；μ4=(1+2ν)/(1-ν)；μ5=1/(2-2ν)；μ6=(1-2ν)/(1-ν)；μ7=(3-2ν)/(1-ν)；μ8=(1-2ν)/(4-4ν)；α=1/ρ。

当ρ=1时，可得圆形土洞洞边的应力表达式，如式(13)～(15)所示。

σθ=-μ1μ2+0.5μ3(1+0.5μ4+0.5μ2-2μ5)·

sinθ-2μ1μ6cos 2θ+μ3μ6sin 3θ，

(13)

σρ=0，

(14)

τρθ=0。

(15)

应力分量由极坐标向直角坐标的变换关系式[22]为：

σx=σρcos2θ+σθsin2θ-2τρθsinθcosθ，

(16)

σz=σρsin2θ+σθcos2θ+2τρθsinθcosθ，

(17)

τxz=(σρ-σθ)sinθcosθ+τρθ(cos2θ-sin2θ)。

(18)

将式(13)～(15)代入式(16)～(18)可得x-z平面直角坐标系下圆形土洞在重力作用下洞边的应力表达式，如式(19)～(21)所示：

sin3θ-2μ1μ6sin2θcos 2θ+μ3μ6sin2θsin 3θ， (19)

2μ5)cos2θ·sinθ-2μ1μ6cos2θcos 2θ+

μ3μ6cos2θsin 3θ，

(20)

sin2θcosθ+μ6(2μ1cos2θ-μ3sin 3θ)sinθcosθ。

(21)

当考虑地下水时，圆形土洞受力分析如图 3(b) 所示，并取直角坐标系K2，本研究仍然将土洞作为深埋空洞处理，根据文献[21]，则必须满足dw>5r。

(2)土洞为椭圆形时

图1(e)～(h)为椭圆形土洞的情况，不考虑地下水时，圆形土洞受力分析如图4(a)所示，并取坐标系K3。

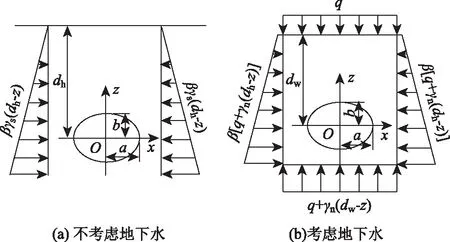
图4 椭圆形土洞受力分析Fig.4 Force analysis on ellipse soil cave

文献[18]对上述问题进行了求解，由于应力表达式冗长，本研究仅给出计算步骤：

① 令q=0，并将dh，γs，z替换文献[18]中的d，γ0，y便可得到椭圆形土洞在自重作用下的应力表达式。

②令ρ=1，可得在复平面内椭圆形土洞洞边的应力表达式。

③将复平面内椭圆形土洞洞边的应力表达式转换为直角平面内的应力表达式，转换关系如式(22)所示[23]。

(22)

式中，θ为复平面极坐标系的角度；θ1为直角平面极坐标系的角度。

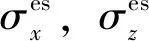
当考虑地下水时，椭圆形土洞受力分析如图4(b) 所示，并取坐标系K4，本研究仍然将土洞作为深埋空洞处理，根据文献[21]，则必须满足dw>5a。

2.3 土洞稳定性评价

将基础荷载作用下产生的应力与土洞洞边在重力作用下(考虑地下水或不考虑地下水)产生的应力叠加，可得到基础荷载作用下的土洞洞边应力表达式：

σx=ψx+φx，

(23)

σz=ψz+φz，

(24)

τxz=ψxz+φxz，

(25)

在利用式(23)～(25)对应力进行叠加时，统一按切应力以顺时针方向为正、压应力为负、拉应力为正。

则可求得相应的最大、最小主应力为：

(26)

(27)

土体极限平衡状态时的莫尔圆与抗剪强度包线的关系如图5所示。

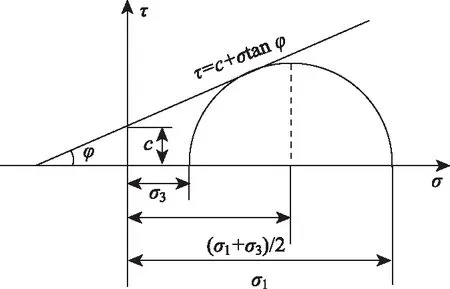
图5 Mohr应力圆与强度的关系Fig.5 Relationship between Mohr stress circle and strength

图5中，c为土体的黏聚力；φ为土体的内摩擦角；τ为切应力；σ为正应力。

由图5可得土体破坏时的条件：

(28)

式(28)中规定压应力为正，拉应力为负，与式(26)、式(27)中符号规定相反，因此，将式(26)、式(27)代入式(28)时，需对符号正负号进行变换。若：

(29)

则可判断土体破坏，土洞处于不稳定状态；反之，土洞处于稳定状态。

2.4 土洞稳定性评价计算步骤

为了便于分析，给出了不同工况下的分析步骤，如图6所示。

(1)对基础荷载作用下的地层应力进行求解：基础荷载作用于地层表面时，采用 Boussinesq解积分式求解；基础荷载作用于地层内部时，采用Mindlin解积分式求解。

(2)建立土洞在自重影响下应力场的计算模型，基于复变函数的方法对考虑地下水或不考虑地下水时，圆形土洞或椭圆形土洞在自重影响下的应力场进行求解，并得到土洞洞边应力分量的表达式。

(3)将基础荷载作用下的地层应力表达式与土洞在重力作用下洞边应力分量的表达式进行叠加，得到基础荷载作用下的土洞洞边应力分量表达式。

(4)引入Mohr-Coulomb屈服准则，对土洞洞边上的点进行验算，从而判断土洞是否稳定。

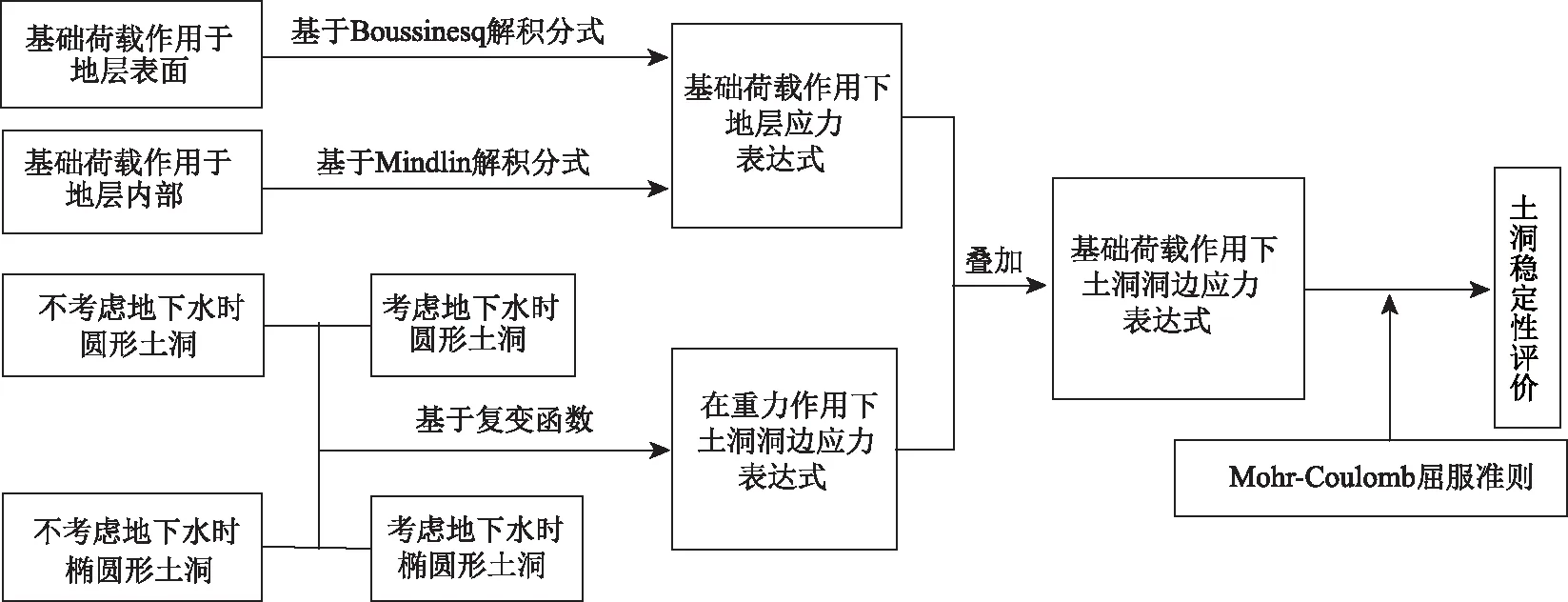
图6 土洞稳定性评价计算过程Fig.6 Calculation process of soil cave stability assessment

3 算例

某工程[2]采用1.6 m×1.6 m的独立柱基，如图7所示。基础埋深为1 m，基底以下为硬塑黏土，地下水为潜水，水位埋深为地面以下1.8 m,硬塑黏土承载力标准值fk=200 kPa，黏土重度γs=18 kN/m3，c=50 kPa，φ=26°，基底附加应力P0=180 kPa，基础底面以下5.0 m 处有一洞高为0.60 m的土洞，土洞内无充填物，硬塑黏土侧压力系数β取0.5。

图7 工程概况(单位：m)Fig.7 Project profile(unit:m)

该工程实例与本研究图1(d)的情况一致，此时s=1 m，h=1.8 m，dw=4.5 m，dl=-0.8 m，ξ=1.6 m，r=0.3 m，q(l)=180 kPa，γn=8 kN/m3。

由于该问题为轴对称问题，本研究按照文献[2]的做法，取a(θ=0°)、a(θ=30°)、a(θ=60°)、a(θ=90°)作为土洞稳定性的验算点。根据图6给的计算步骤，可得应力计算结果如表1所示。

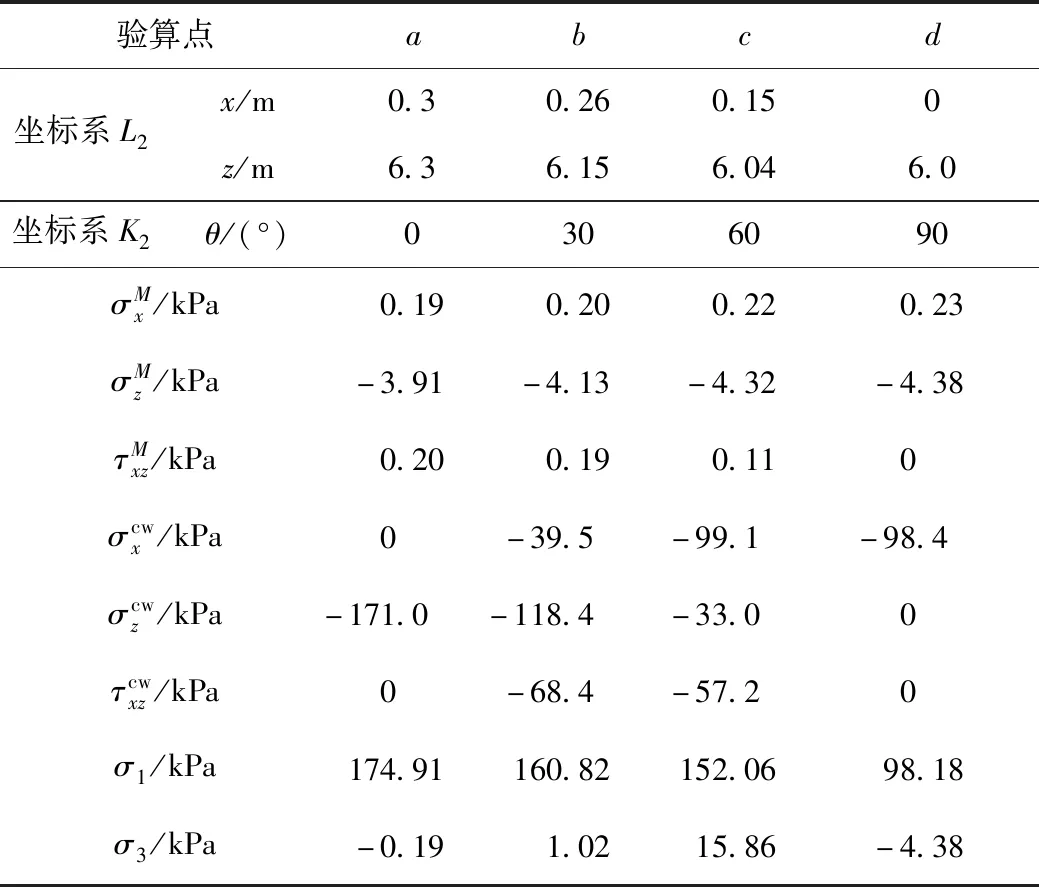
表1 应力计算结果Tab.1 Stress calculation result

将σ1，σ3代入式(12)，可知a，b，c，d均处于稳定状态，因此可以判断该土洞在基础荷载作用下稳定，这与文献[2]所得结论是一致的。

4 结论

(1) 根据土洞上方基础的承载特性，综合考虑了地下水、土体自重、溶洞形状对土洞稳定性的影响，提出了8种不同条件下土洞稳定性计算模型，为基础荷载作用下土洞的稳定性分析奠定了基础。

(2) 通过对Boussinesq解、Mindlin解进行积分，得到基础荷载作用在地层表面、地层内部时地层应力表达式，并基于复变函数方法求得土洞在自重影响下的洞边应力，将二者叠加得到了基础荷载作用下土洞洞边应力状态。

(3) 根据应力分量求得最大、最小主应力，引入Mohr-Coulomb屈服准则，选取离基础较近的土洞周围的关键点进行验算，从而对土洞稳定性进行评价。