Solitary wave solutions for the variable-coefficient coupled nonlinear Schrödinger equations and Davey-Stewartson system using modified sine-Gordon equation method

Reh M. El-Shiekh Mhmoud Gllh

a Department of Mathematics，College of Science and Humanities at Howtat Sudair， Majmaah University， 11952， Saudi Arabia

b Department of Physics， College of Science at Al-Zulfi， Majmaah University， 11952， Saudi Arabia

c Department of Mathematics， Faculty of Education， Ain Shams University， Cairo， Egypt

Received 29 July 2019; received in revised form 29 October 2019; accepted 29 October 2019

Available online 19 November 2019

Abstract In this study，the sine-Gordon equation method is modified to deal with variable-coefficient systems containing imaginary parts，such as nonlinear Schrödinger systems. These are of considerable importance in many fields of research，including ocean engineering and optics. As an example，we apply the modified method to variable-coefficient coupled nonlinear Schrö dinger equations and Davey-Stewartson system with variable coefficients，treating them as one-dimensional and two-dimensional systems，respectively. As a result of this application，novel solitary wave solutions are obtained for both cases. Moreover，some figures are provided to illustrate how the solitary wave propagation is determined by the different values of the variable group velocity dispersion terms，which can be used to model various phenomena.

Keywords: Coupled nonlinear Schrödinger equations; Davey-Stewartson system with variable coefficients; Sine-Gordon equation method; Solitary waves.

1. Introduction

Nonlinear partial differential equations (NPDEs) are used to model many phenomena in the fields of physics，plasma and engineering. One of the most significant NPDEs is the nonlinear Schrödinger (NLS) equation，it can describe the nonlinear dynamics of surface gravity waves in oceans and is an approximation of the fully nonlinear equations，it contains the two basic ingredients of surface wave dynamics:nonlinearity and dispersion (in an oceanographic context). Besides this，the equation can be used to describe many different physical systems，such as nonlinear optics，plasma waves and condensed matter.

Owing to its importance，many new techniques have been developed to solve the NLS equation，these including classical Lie groups，Steinberg’s symmetry method，Clarkson and Kruskal (CK) direct similarity method，Darboux transformation，Painlevé test，integral methods，Bäcklund transformation，consistent Riccati expansion solvability，etc. [1-38] .

The sine-Gordon equation method is one of the more recent techniques developed [39，40] ，in this paper we make a set of modifications to this method，so as to apply it to variablecoefficient systems containing imaginary parts，such as NLS models. As an example，we apply it to the coupled nonlinear Schrödinger (CNLS) equations，which describe the evolution of two orthogonally polarized optical pulses [41，42] ，given by

whereψ1andψ2are the slowly varying amplitudes of two orthogonally polarized optical pulses，andx，andtare the normalized propagation distance and retarded time，respectively.The coefficientsβ(x) andg(x) represent the group velocity dispersion (GVD) and the Kerr nonlinearity coefficients，respectively [41，42] . Whenβ(x) andg(x) are set as constants，the above CNLS equations describe phenomena such as orthogonally polarized complex waves，they not only admit solitons-which allow energy redistribution between the modes upon collision but also lead to logical-computing and，in hydrodynamics，govern the evolution of cross sea waves [43] .

Moreover，we apply the modified sine-Gordon equation method to the variable-coefficient Davey-Stewartson (vcDS)system;

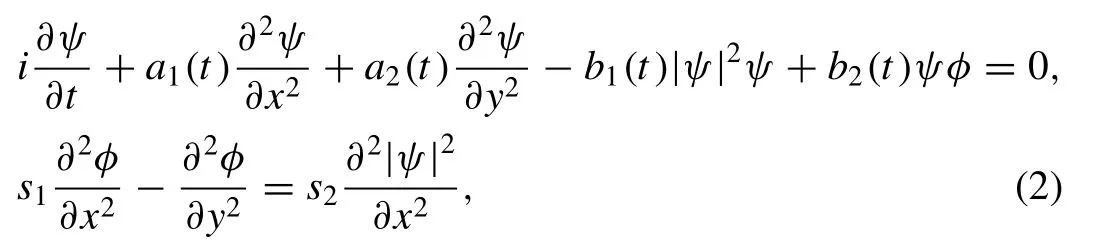
whereψ=ψ(x，y，t) is the complex wave envelope，φ=φ(x，y，t) is the real forcing function，a1(t) anda2(t) are real functions int，representing the GVD terms，andb1(t) andb2(t)are the cubic nonlinear coefficient and quadratic nonlinearity term，respectively. Lastly，s1ands2are constants. The Davey-Stewartson system (DS) is an important extension of the (1+ 1)-dimensional NLS equations，it was first introduced to describe a (2 + 1)-dimensional wave packet on the surface of a liquid of finite depth [44] when the variable functions are constant. The DS equations and their extended forms have attracted much attention and been found suitable for a variety of applications [44，45] . Therefore，we have chosen the vcDS as the subject upon which to apply our novel modification of the sine-Gordon equation method.

2. Modified sine-Gordon equation method

In this study，we make a series of modifications to the sine-Gordon equation method [39，40] ，so as to be able to use it for variable-coefficient NPDE (vcNPDE) systems containing imaginary parts，of the form

whereβ(x) andg(x) are arbitrary functions inxandk=1，2.With the following steps，Eq. (3) can be reduced directly to a system of nonlinear ordinary differential equations

1. Use the following assumptions:

whereU1(ζ) andU2(ζ) are the new dependant functions，ζ=μ(t-λ(x))is the new independent variable，λ(x) is an arbitrary function ofxandμandαare the frequency and the width of the soliton，respectively.

2. Collect the coefficients ofU1(ζ) andU2(ζ) and their derivatives，then assume that the imaginary part is equal to zero.

3. Take the coefficient of the greatest linear term as a normalization coefficient，then equate the derivatives and powers ofU1(ζ) andU2(ζ) with that term multiplied by a constant，so the arbitrary functions will be determined and the vc-NPDE system of Eq. (3) is transformed into the following nonlinear ordinary differential system.

4. Use the solutions of the sine-Gordon equation [39，40] by assuming that

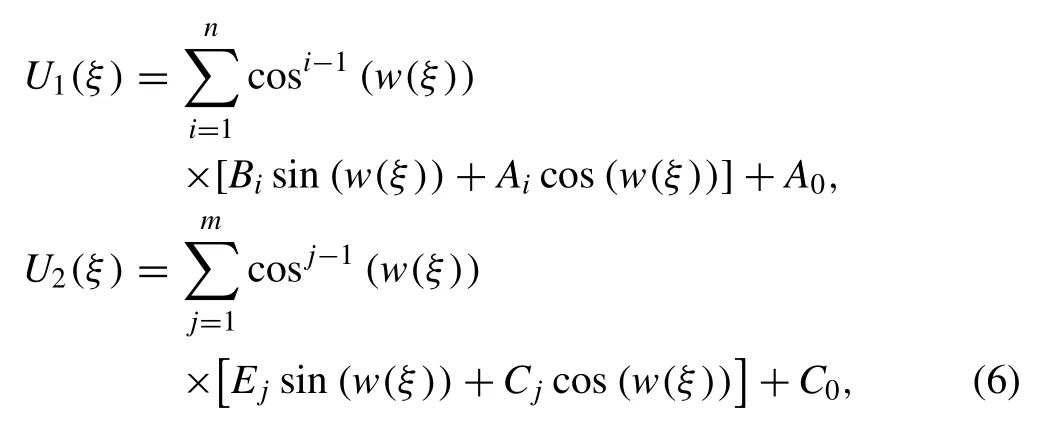
and

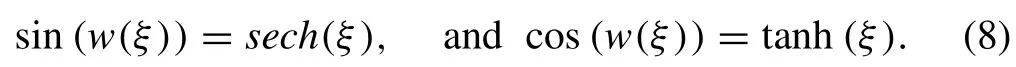
finally by collecting the different coefficients of sin (w(ξ))and cos (w(ξ))，then equating them to zero，an algebraic system for the constantsAi，Bi，Cj，Ej，A0andC0is obtained，by solving it with a Maple program and backsubstituting into Eqs. (6) and (4) via Eq. (8) ，novel solitontype solutions are obtained for the system of Eqs. (3) .

3. Solitary wave solutions for CNLS

By substituting the assumptions in Eq. (4) into CNLS we obtain

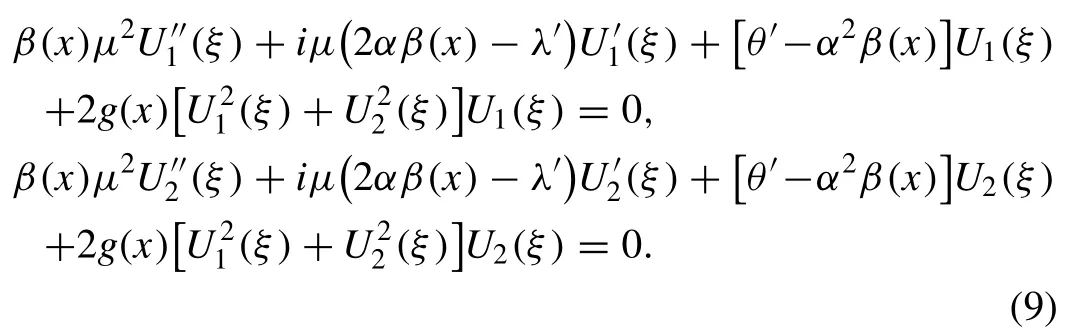
to make this system (E q. (9)) real，the term smust be eliminated，therefore we set，then by using the coefficients ofas the normalization coefficient，we get

wherec1andc2are constants andθ0is an integration constant. Therefore，

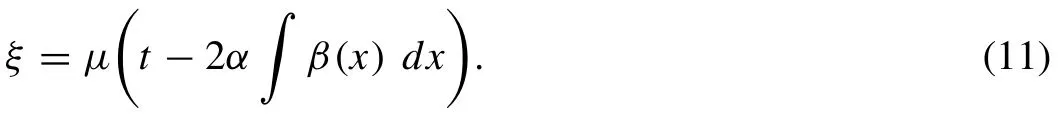
and Eq. (9) is reduced to

By balancing the linear and nonlinear terms in this system( Eq. (12) ) we getm=n= 1，then we assume that

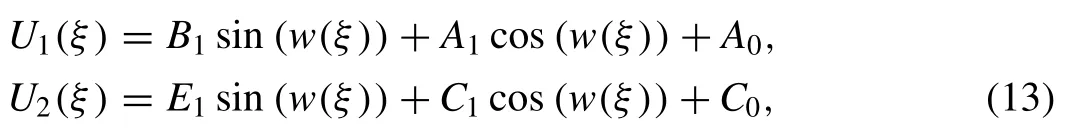
and substitute it into Eq. (12) using Eq. (7) ，then by collecting the coefficients of sin (w(ξ)) and cos (w(ξ))，and equating them with zero，an algebraic system is obtained，which can be solved using a Maple program. The following cases for the undetermined constants are obtained.

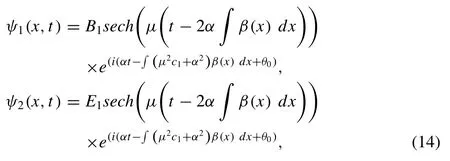
whereB1andE1are arbitrary constants.

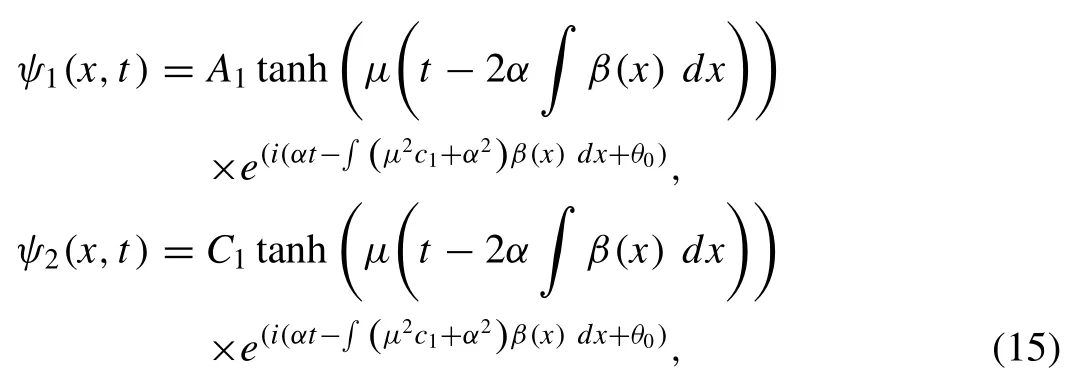
whereA1andC1are arbitrary constants.

4. Solitary wave solutions for vcDS system

Now，we apply the sine-Gordon equation method to the vcDS system (Eq. (2))，by assuming that

withξ=μ1x+μ2y-λ(t)，whereμ1，μ2，k1andk2are arbitrary constants.λ(t) andθ(t) are arbitrary functions oft. By using the same procedure as before，the vcDS system can be reduced to the following nonlinear ordinary system

with the following relations obtaining between the variable coefficients:

whereb1，b2andθ0are arbitrary constants. Integrating Eq. (18) twice with respect toξ，we get

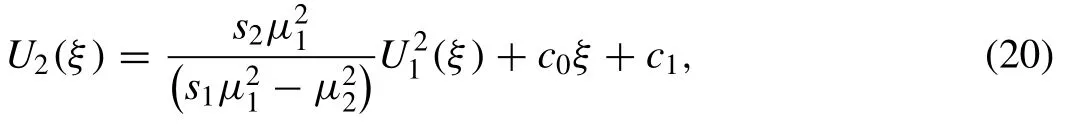
wherec0andc1are integration constants. By substituting Eq. (20) into Eq. (17) we get

This equation can be solved by the sine-Gordon equation method，wherec0must be eliminated，then it can be rewritten as

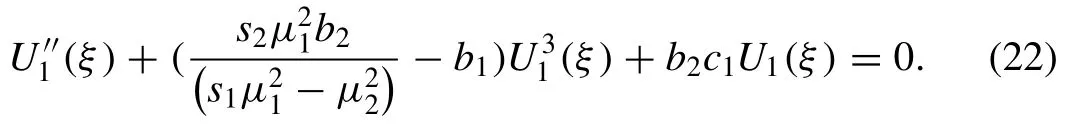
From the balance method we find thatm=n= 1，then we assume that

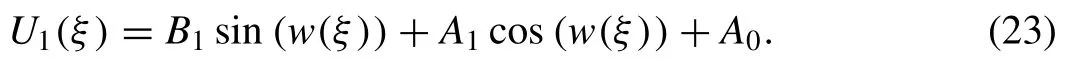
Substituting from Eq. (23) into Eq. (22) using the assumptions in Eq. (7) ，then by collecting the different powers of sin(w(ξ))and cos(w(ξ))and equating them to zero，an algebraic system for the constantsA0，A1andB1is obtained. By solving this with a Maple program the following novel solitary solutions are obtained for the Davey-Stewartson system with variable coefficients.

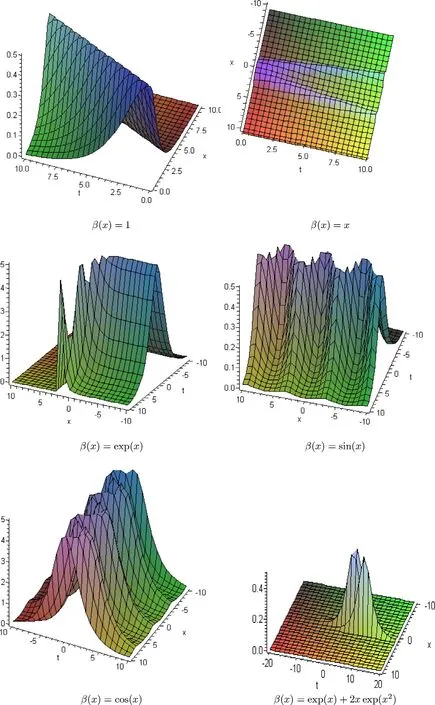
Fig. 1. Propagation of bright solitary wave solution of CNLS，plotted for different values of β( x ).

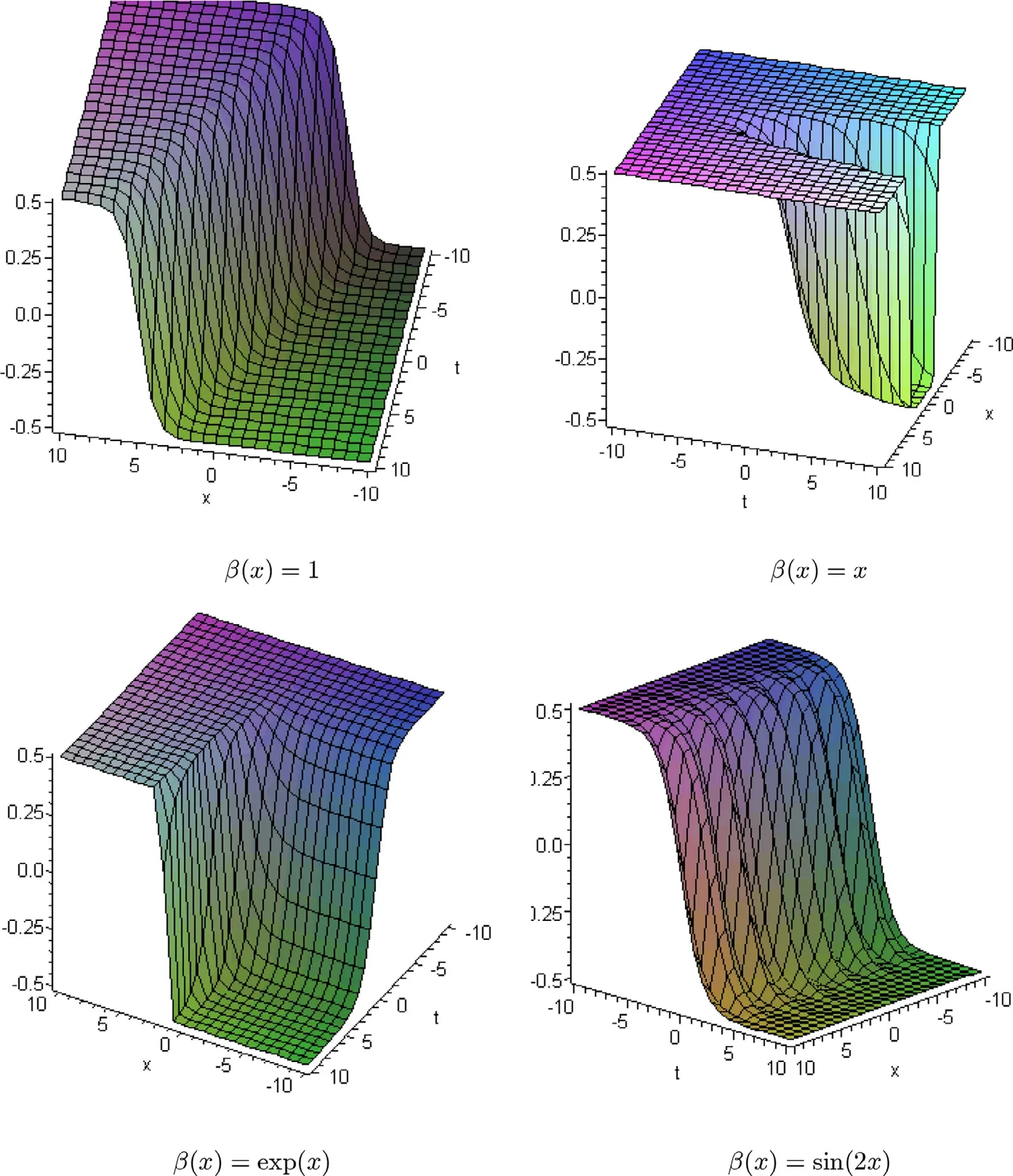
Fig. 2. Propagation of dark solitary wave solution of CNLS，plotted for different values of β( x ).

5. Physical application

The novel bright and dark solitary waves were obtained in the previous sections for both the CNLS equations and vcDS system，therefore in this section we investigate the propagation behavior of both the bright solitary wave solution |ψ1|given by Eq. (14) ，and the dark solitary wave solution |ψ1|represented by Eq. (15) of the CNLS equations，illustrated in the following figures.

In Fig. 1，the propagation of bright solitary wave solution|ψ1| of CNLS is determined by the different chosen values ofβ(x) ，we can see that it propagates as a parabolic bright soliton whenβ(x) =x，as a periodic bright soliton whenβ(x)= sin(x)orβ(x) = cos(x)or as two bright solitons whenβ(x) = exp(x)+ 2xexp(x2).With fixed parametersB1=μ=andα= 1.

In Fig. 2，the dark soliton solution |ψ1| of the CNLS equations，given by Eq. (15)，is drawn for the case whereβ(x) is set as 1，x，exp (x) and sin (2x) ，respectively，and the fixed parameters are chosen asFrom these figures we can see that the dark soliton propagates as an ordinary dark soliton，parabolic dark soliton and periodic dark soliton，determined by the different values of the variable coefficientβ(x).

6. Conclusion

In this study，the sine-Gordon equation method is modified so as to be applicable to systems with variable coefficients containing imaginary parts. As a novel demonstration of its implementation on such systems in one- and two-dimensional scenarios，we have applied it to CNLS equations and the vcDS system. As a result，new solitary waves are obtained，which could have applications in several branches of physics，such as hydrodynamics，ocean engineering，and optics. We plotted the bright and dark solitons for the CNLS equations using different values of the variable coefficientβ(x)，and found that the propagation of the solitary wave is determined by this value.

Finally，from this study we put forward the following remarks on the new modified sine-Gordon equation method.

1. The new modified sine-Gordon method gives soliton solutions for variable-coefficient systems such as CNLS and vcDS directly，without difficult calculations (see [41-45] ).

2. By comparison with other methods，we can conclude that the modified method is easier and more powerful than its alternatives，this can be clearly seen in our demonstration[41-45] .

3. The new modified sine-Gordon method could be applied to many systems in ocean engineering [46-48] .

Acknowledgment

The authors would like to thank the Deanship of Scientific Research，Majmaah University，Saudi Arabia，for funding this work under project No. R-1441-26.