时频谱熵属性在春光油田储层预测中的应用研究

肖 学，田仁飞，赵乾辰

（1.中石化河南油田分公司勘探开发研究院，河南郑州450018；2.成都理工大学地球物理学院，四川 成都610059）

春光油田位于准噶尔盆地车排子凸起区域，纵向上在沙湾组发育多套岩性油气藏，利用地震振幅类属性［1］、电阻率参数［2］能够较好的识别该类岩性储层，但油水识别困难。 因此，有必要发展适合春光油田的储层预测油水识别方法。 储层中含流体（油或水）后会改变地震信号的频谱特征，这种频谱特征的变化可用熵表示。 从信息角度看，熵表征信号的微小变化的有序状态， 有序信号具有小的熵值，而无序信号具有较大的熵值［3］。储层含油气后，熵值会增大。 时频谱熵是不同频率的熵的融合体，对信号的无序反应灵敏，该参数在储层预测［4］、滚动轴承故障识别［5］中取得了较好的应用效果。然而，现有的时频谱熵计算方法由于精度不高、 分辨率较低，为了获得高精度的时频谱熵，设计一种高精度的时频分析方法至关重要。 改进广义S变换是在S变换［6］的基础上，通过拓展广义S变换中的小波基函数为任意可变的函数来提高时频分辨率，而通过调节广义S变换中的参数因子使其能够获得更高精度的时频分辨率，具有灵活性［7-8］，为此，我们结合信息熵的算法，发展了基于改进广义S变换的高精度时频谱熵算法，并将其用在春光油田C22井区的含油储层预测中，获得了较好的实际应用效果。

1 基本原理

1.1 时频变换的原理

时频变换作为一种常规的地震信号分析方法在地震储层预测中得到了广泛应用。 常用的时频变换方法主要有短时傅里叶变换、连续小波变换、Wigner-Ville变换［9］。 近几年，发展了S变换及其改进算法， 由于S变换可以根据信号的特点自适应的调节窗函数，获得较高精度的时频分辨率，因此，在地震信号分析中具有更好的应用效果［10］。 本文主要用到以上时频变换的正变换，下面做简要论述，详细的理论分析和各种时频变换方法的性质、特点等参考文献［6］、［9］［6、9］。

1.1.1 短时傅里叶变换

短时傅里叶变换是经典的时频变换方法，它将时间域的信号变换到时频域二维的表达形式，从而获得信号的时频特征。 其核心思想是在傅里叶变换的基础上加滑动短时窗（通常加高斯窗），并假定信号在这短时窗中是平稳信号，由此短时傅里叶变换（STFT）定义为

式中，STFT（t，f）为短时傅里叶变换，t为时间，s；τ为时间延迟，s；f为频率，Hz；x（τ）为时间域信号，g（τ-t）为窗函数，无量纲。 短时傅里叶变换时频分辨率受窗函数长度影响较大，通常要获得较高时间分辨率需要短时窗，而要获得较高频率分辨率需要长时窗。 实际应用中，可以根据信号的特征来调整窗函数大小。

1.1.2 连续小波变换

在L2（R）空间，信号x（τ）的连续小波变换定义为

1.1.3 Wigner-Ville变换

信号x（t）的Wigner-Ville变换可以定义为

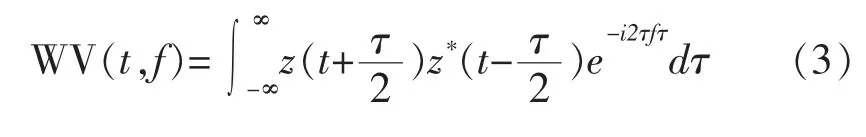
式中，WV（t，f）为Wigner-Ville分布，t为时间，s；f为频率，Hz；z（t）为x（t）的解析信号［9］，无量纲。Wigner-Ville分布是一种分析非平稳信号的重要工具，具有较好的时频聚集性，但对于多分量信号受交叉项的影响较为严重，常造成信号的时频特征模糊不清，通过加窗平滑在一定程度上能够改善交叉项的影响。

1.1.4 改进广义S变换

Stockwell在1996年提出了S变换算法，该算法的核心是在地震信号x（t）的连续小波变换（CWT）［11］的基础上， 将S变换定义为一个小波变换与特定函数的乘积，并经过重新整理S变换的公式，其表达形式为

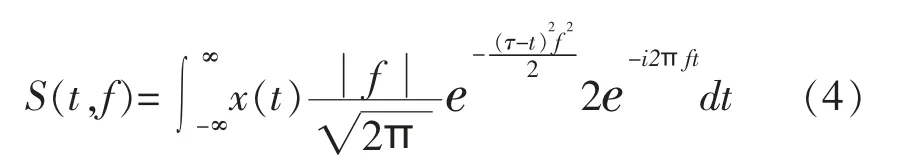
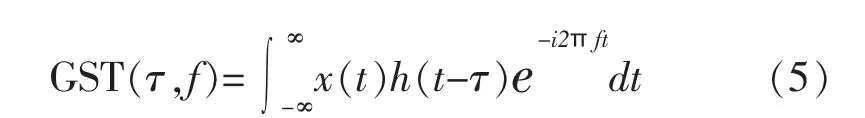
式（4）和（5）中，t、τ、 f参数与式（1）一致。为了获得更高的时频分辨率， 在广义S变换做了进一步改进，增加了两个调节因子参数，改进的广义S变换公式可以改写为［7-8］

式（6）中，频率f≠0，参数S和r均为调节因子，无量纲，且S＞0，r＞0这就是改进的广义S变换。

1.1.5 时频变换对比分析

为了验证改进的广义S变换在时频分辨率上比其他时频分析方法更具优势，我们利用单道地震信号对比分析了短时傅里叶变换（STFT）、连续小波变换（CWT）、Wigner-Vile变换和S变换，其结果如图1。图1中短时傅里叶变换由公式（1）计算，时窗为高斯窗函数， 时窗大小按照计算信号1/6长度自动调节；连续小波变换由公式（2）计算，采用MATLAB软件包自带的函数CWT，尺度长度256，用morlet作为小波基函数；Wigner-Vile分布由公式（3）计算，未加滑动时窗做平滑处理；S变换由公式（4）计算；广义S变换由公式（5）计算，利用频率窗宽度随频率f呈反比变化高斯窗函数［8］；改进的广义S变换采用公式（6）计算，经过试验，当s和r调节因子均为0.5具有较好的时间分辨率。 从图1可知：S变换在时频分布图上能量相对集中，图像也比较光滑；而Wigner-Vile变换受交叉项影响较大；短时傅里叶变换时间分辨率较低，主要受时窗大小影响较为严重；小波变换纵向时间分辨率较低，而横向频率分辨率较高。 总体而言，S变换可以通过改变小波基函数获得较高的时间、频率分辨率，这在地震信号时频变换应用中展现了较好的优势。 进一步对S变换进行改进，其计算利用式（6），通过调节s、r因子和优选一般形式的基函数，可以提高时频分辨率，体现了广义S变换的灵活性。 为了突出对薄储层识别能力，参数选择时候更多考虑突出时间分辨率。 由图2可知：改进的广义S变换能量更为集中，横向时间轴也可以分离（图中虚线方框内），因此，改进的广义S变换具有更高的时间分辨率， 更适合薄储层的地震响应特征的计算，即使频率分辨率有一定降低，但仍满足高精度时频谱熵属性的计算。

图1 几种时频变换对比

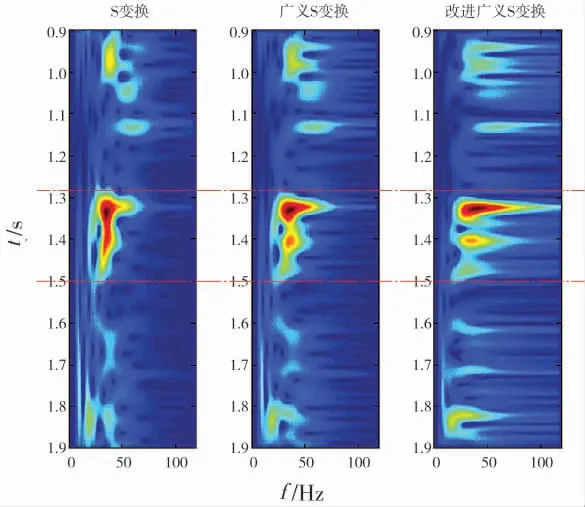
图2 改进广义S变换时频对比

1.2 时频谱熵算法原理

利用公式（7）计算地震信号每一时间点的瞬时能量谱，在地震信号有效频带范围内，利用概率密度函数为［4］

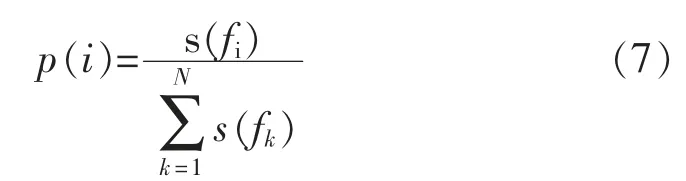
式（7）中，S（fi）是fi的能量，P（i）是对应的概率密度，N是信号通过改进的广义S变换后频率成分的所有点数，均为无量纲参数。

通过对地震信号采用时频变换后，利用式（7）得到概率密度函数，根据谱熵的定义，时频谱熵的计算公式为

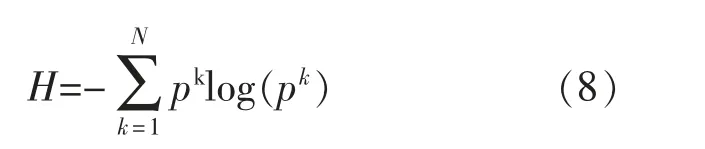
式（8）中，H为时频谱熵，p为概率密度函数，k为时间样点，均为无量纲参数。 利用公式（8）计算所有地震信号的时频谱熵后，可以根据储层与非储层的时频谱之间的差异进行储层含油性预测。

2 应用实例

春光油田主要是以岩性油藏为主，位于准噶尔盆地西北部车排子地区［12］。 目标层为沙湾组T2砂组砂体，该储层段砂岩表现出较强的非均匀性，以砂泥互层、泥包砂岩相组合为特征，储层薄、孔隙度高。其中，根据C22井测井解释结果显示：C22井的测井储层解释厚度仅4.5 m，平均孔隙度为28.97%。 目前该地区沙湾组的含油砂体、含水砂体的地震响应特征区分不太明显，导致利用地震资料进行油水识别困难。 为了探索时频谱熵对油水识别的能力，我们从已知钻井出发，统计了工区已钻7口井沙湾组T2的试油情况，如表1。并提取通过C108、C22-3、C22井的联井地震剖面，如图3a。 由图3a和表1可知：C22井沙湾组储层在地震上表现为强振幅特征，而未获得工业油流的C108井目标层段振幅响应较弱。 实际钻井表明C22-3为油水分界面， 但在图3a的地震剖面上与C22油井地震振幅区分较小。 这里，我们利用上述时频谱熵计算原理， 计算了多种时频谱熵数据体。 由图3的时频谱熵可知：几种时频谱熵的计算方法都能够反映T2储层特征和分布 （图中虚线框所示）。但Wigner-Ville变换由于受交叉项影响，时间分辨率较低， 其计算时频谱熵的时间分辨率也较低；而连续小波变换计算的时频谱熵T2层下方高值异常（图3d），可能是受T2层下方强反射轴的影响较大，其他几种方法受强轴影响相对较小。 综合时间分辨率和能量聚集度综合考虑，改进的广义S变换计算的时频谱熵属性效果最佳。 时频谱熵在区分油水储层也有一定识别能力，如图3f中油水同层C22-3井处于时频谱熵的能量相对较弱区域的边界，道号约80～110可解释为水层；道号约110～240解释为油层，其它为非储层。

表1 工区钻井沙湾组T2试油情况统计表

为了更好的展示时频谱熵对储层的识别能力，沿层T2提取了原始地震资料的瞬时振幅属性（图4）和基于改进的广义S变换计算的时频谱熵（图5）。 从图4可知： 瞬时振幅属性能够较好的识别储层与非储层，与表1实际钻井结果吻合，但储层中油、水难以区分。 由图5中，除了能够较好的区分储层与非储层外，还能够较好的区分含油储层和含水储层，且C22-3处于油水分界面的边界，C22-2时频谱熵为中低值，应为非油层，实际试油为水层，与表1实际试油结果吻合。 上述利用时频谱熵检测方法，与瞬时振幅属性的分析结果相比，认为时频谱熵比瞬时振幅属性更能够较好的识别含油储层，具有较好的实用性。

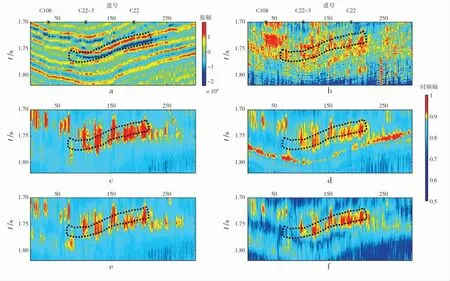
图3 过C108、C22-3、C22井的联井地震剖面及时频谱熵

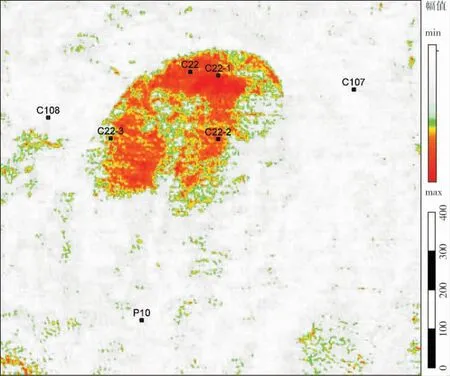
图4 沙湾组沿层瞬时振幅属性

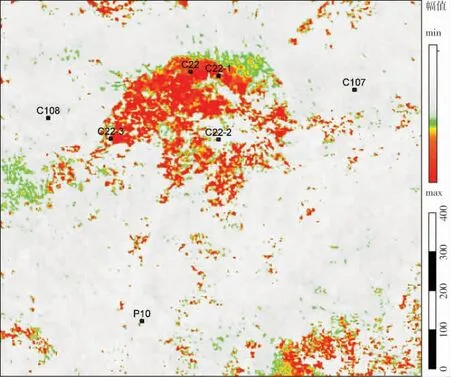
图5 沙湾组沿层时频谱熵

3 结论

（1）通过对比分析Wigner-Ville变换、S变换、短时傅里叶变换和改进的广义S变换等时频变换方法， 由于改进的广义S变换能够通过调节因子参数获得更高的时间分辨率，更能够满足高精度的时频谱熵的计算。

（2）油水识别的关键是具有灵敏度高的地震属性，而时频谱熵能够表征地震信号对油水反应的有序性，岩石中充填不同流体，其时频谱熵不同，时频谱熵的振幅值相对较大更能够刻画储层含油层的地震响应特征。

（3）时频谱熵对地震响应的微弱变化较为灵敏，而引起地震信号变化的因素较多，文中应用实例在受构造影响较小的岩性油藏取得了较好效果。实际应用中需结合工区地质、钻井等资料进行标定，并可进一步拓展到页岩油、页岩气等非常规油气预测中。