自适应噪声抵消系统的MATLAB仿真与分析*

于新颖

(山西大学商务学院 信息学院，山西 太原 030031)

0 引言

噪声可以说无时无刻不存在于我们的生产和生活环境中，对有用信号构成了干扰，尤其是在医学有用信号的提取及军事通讯等领域中，其噪声更是存在着巨大的干扰甚至危害[1]。故，关于用来抑制噪声甚至消除噪声的自适应的噪声抵消系统的研究慢慢地变成了热点话题[2]。目前，对于自适应的噪声抵消系统的探讨包括算法的改进、滤波器结构的完善以及参考信号的获取等方面[3]。本文尝试采用基本的LMS算法，在模拟输入信号及干扰噪声的条件下，观察设计的自适应噪声抵消系统对于输入信号的噪声抵消效果，从而体现其在消噪方面的作用。

为了直观地观测到输出波形曲线的变化情况，并减少大量语言编程的工作量，本文采用目前信号处理方面经常应用的MATLAB软件，用其来进行自适应噪声抵消系统的仿真与分析。MATLAB软件是由MathWorks公司研究生产的商业数学应用软件，其主要包含的两大功能部件一是Simulink，可完成的功能主要包括动态创建及更改系统模型，模型的仿真验证及系统的功能分析等；另一功能部件是编程界面，可完成信号算法的编程设计并自带图形仿真功能，能直观地看到信号的曲线变化情况。MATLAB经常应用的场合包括嵌入式的系统设计、信号的分析和处理、线性及非线性的系统控制等领域。具有应用领域广泛、界面简洁及上手容易等优势。

所以，借助MATLAB中的编程界面来完成LMS自适应噪声抵消系统的建立及仿真分析[4]，设计者能通过较简单的算法编程实现所设计的电路、并能形象地看到此系统对于信号的处理前后效果对比图，这也比较符合当前电路设计的基本趋势。

1 MATLAB里构建LMS自适应噪声抵消系统

1.1 LMS自适应噪声抵消器工作原理

当输入信号的部分或全部特性存在未知分量时，可根据某种制定好的优化规则，从滤波器最初设定的滤波器系数开始完成滤波操作。在滤波的过程中，这种滤波器的参数并非是一成不变的，而是在每一个时刻都会按照设定好的噪声抵消算法进行更新，直至到达规定好的递推次数之后，最终根据统计学规律收敛于某一逼近值。所以说，自适应噪声抵消系统具有较强的自我更新和调节能力[5]。而这种能够动态且自动地改善自身的滤波器参数、从而达到最佳滤波的特性，对于输入信号随时变化、周围干扰未知性强的场合，其处理结果经常能达到较好的效果。图1为自适应噪声抵消器结构图。

图1 自适噪声抵消器的结构图

在本文中，自适应滤波器的参数更迭的规律由最小均方误差LMS算法控制。这种算法最早由Widrow以及Hoff提出，它的基本思想是将误差信号的每次迭代更新的瞬时平方值代替其均方值，从而以求降低运算的工作量和复杂度。LMS算法的主要递推公式如下所示：

e(m)=d(m)-WT(m)X(m).

(1)

W(m+1)=W(m)+2·μ·e(m)·X(m).

(2)

其中，X(m)=[x(m),x(m-1),…x(m-M+1)T]为输入信号变量在不同时刻下的取值情况；y(m)为自适应滤波器的输出；d(m)为要逼近的期望信号；e(m)为误差信号，由期望信号和滤波器的输出信号求差产生；μ代表更新的步长，影响着整体噪声抵消效果的收敛速率及最终的稳定性。

1.2 自适应噪声抵消系统的设计

在设计基于LMS算法的自适应噪声抵消系统时，主要设计思路可归纳为：依据LMS自适应噪声抵消器的结构框图和算法原理，利用MATLAB的编程界面完成输入信号和噪声信号的类型及频率的选定，LMS算法的递推编程以及输出曲线的区域布置等。

图2 自适应噪声抵消系统的部分算法

图2是有用信号为正弦信号，参考输入端的干扰信号为随机信号时，基于LMS算法的自适应噪声抵消系统在MATLAB中编程的部分算法文件。

2 自适应噪声抵消系统的MATLAB仿真

设一纯净的未受噪声干扰的有用信号为一频率为1000 Hz的正弦信号(图3左)，噪声信号干扰后波形发生了变化(图3右)，噪声干扰前后的信号对比图如图3所示。

图3 纯净的有用信号与受噪声干扰的原始输入信号对比图

将图3中受噪声干扰的信号经过本文设计的自适应噪声抵消系统之后，处理前后的信号对比图如图4所示(图4左为噪声抵消器输入端信号，图4右为噪声抵消器输出端信号)。

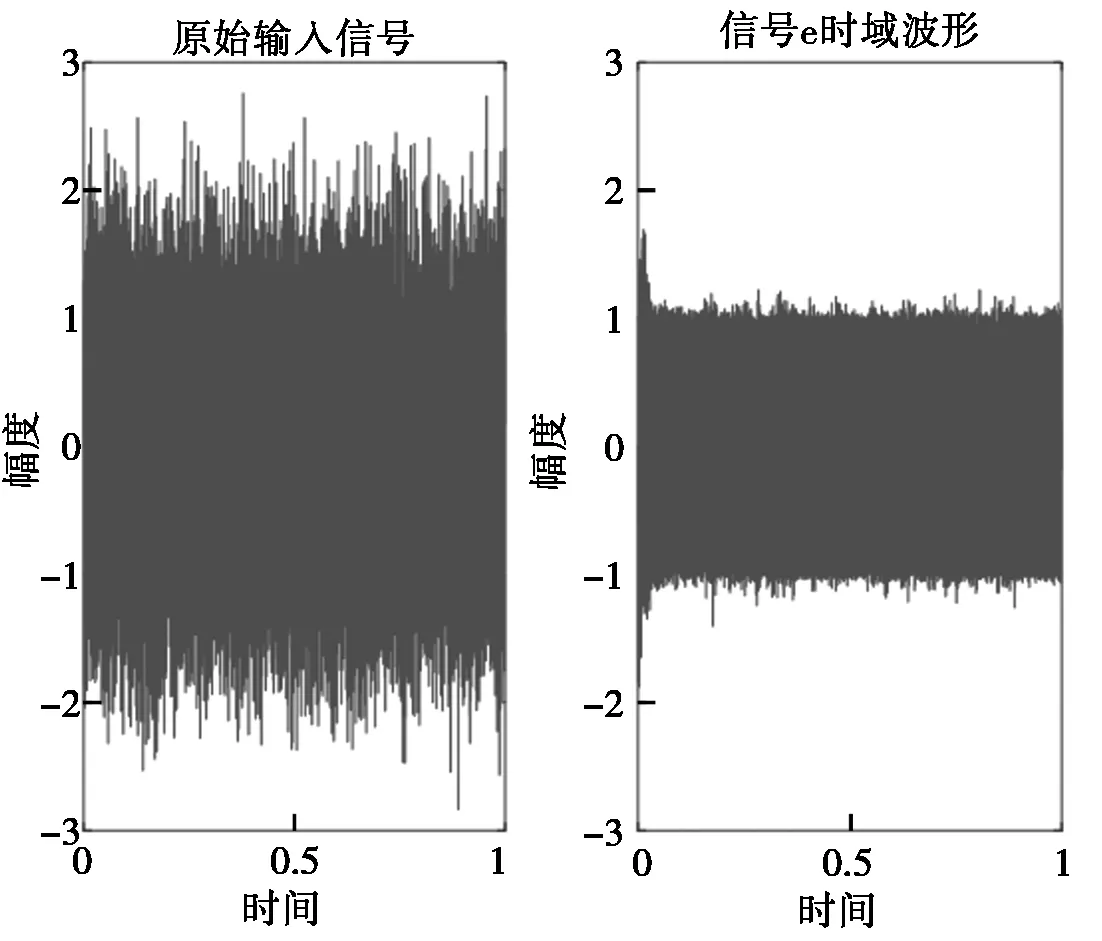
图4 自适应噪声抵消器处理前的原始输入信号与处理后的误差信号对比图

为了更明确地看到被噪声污染的有用信号被噪声抵消器处理之后的还原情况，本文将未被噪声干扰的有用信号(图5左)和虽然被噪声干扰但是经自适应噪声抵消器处理之后的信号(图5右)进行了如图5的对比。

为了便于进一步细致观察噪声抵消的效果，本文将经自适应噪声抵消系统处理之后的信号的曲线图进行了局部放大，如图6所示。

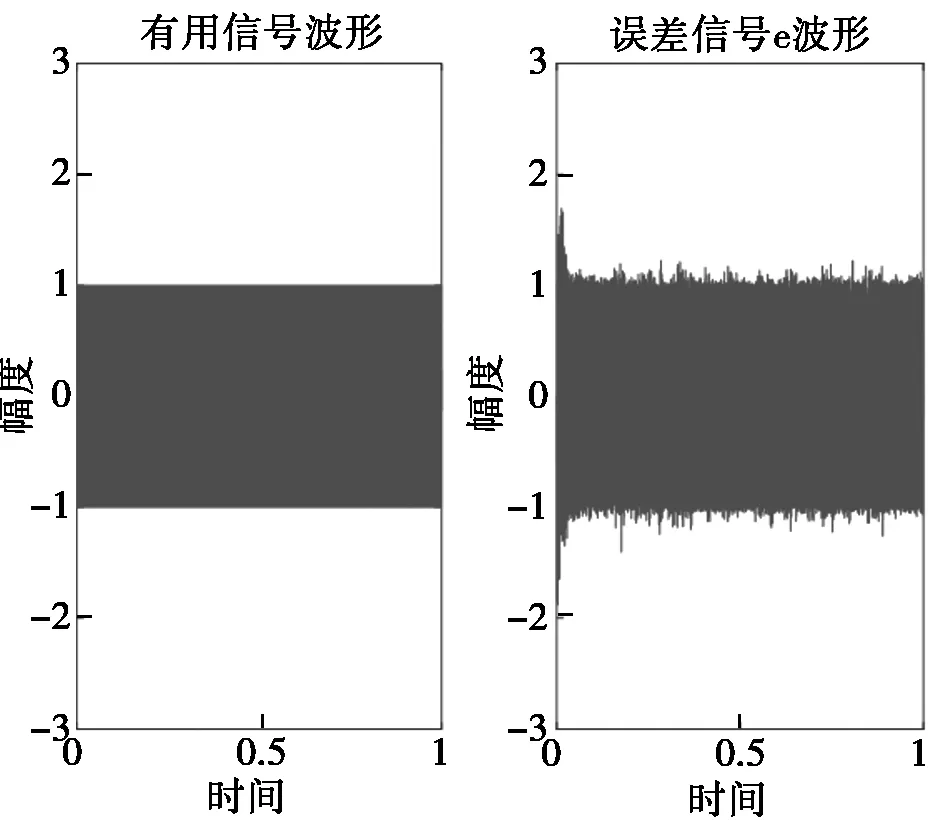
图5 纯净的有用信号与抵消器输出的误差信号对比图

图6 自适应噪声抵消器处理后的信号局部放大图

3 结果分析

由图3可知，有用信号被噪声干扰后发生了较大的变化，有进行消噪的必要；由图4可知，信号经自适应噪声抵消系统处理之后，发生了明显变化，且由图5可知，这种变化的趋势是噪声抵消系统处理之后的信号更接近纯净的未受噪声干扰的有用信号了，即消噪效果显著。这种改善效果通过图6的局部放大图，可进一步得到确认。说明编程设计的自适应噪声抵消系统可达到消噪的目的。

4 结论

本文通过在MATLAB中编程设计基于LMS算法的自适应噪声抵消系统，并对其噪声抵消效果进行了干扰信号的仿真验证，结果说明此自适应噪声抵消系统虽然算法较简单，但是也能达到较好的消噪效果，为进一步的算法改进奠定了基础。