轴流泵内部压力脉动特性及流动诱导噪声研究
孙 奥 冉
(安徽省水利水电勘测设计院,合肥 230088)
0 引 言
轴流泵内部水流的复杂运动状态将会引起泵内部的压力脉动现象,严重时将会加剧泵在运行时的振动、噪声,从而对泵的稳定运行产生影响[1]。泵内部流动噪声主要由水流与叶轮和壳体相互作用产生的定常和非定常力引起的偶极子源所诱发[2],其中转动的叶轮引起的旋转偶极子源是叶片泵与风机等旋转机械特有的声源形式[3]。建立有效的性能预测方法,分析轴流泵内部流动机理以及寻求抑制不良流动的控制手段,同时分析轴流泵非定常压力脉动及流动诱导噪声特性,有利于改善轴流泵的水力性能并提高其运行稳定性。国内外学者就泵内部非定常压力脉动及流动诱导噪声开展了一系列研究,Gonzlez等[4]以离心泵为研究对象,通过试验研究了其内部的非定常流动特性,研究结果表明泵体振动与其压力脉动有着密切关系。王福军等[5]通过对轴流泵进行非定常计算,发现在进行非定常计算时,为取得较准确的数据,压力脉动计算至少为8个周期。施卫东等[6,7]分别对轴流泵和斜流泵进行了非定常数值计算,通过分析得到了水泵进行计算时压力脉动采样时间步长的确定方法。刘厚林等[8]通过对离心泵进行数值计算,并对得到的数据进行时域和频域分析,发现叶片通过频率为离心泵蜗壳内压力脉动的主频。吴仁荣等[9]通过分析船用泵低噪声的原理,分析了水泵噪声与其结构参数的关系,并结合着某船用泵具体实例,提出了水泵降噪的优化方法。袁建平等[10]为了准确研究泵内部非定常流动产生的机理,首先对某泵型采用了4种设计方案,并对每种设计方案的模型泵进行数值计算和PIV模型试验,通过对比两者之间得到数据的差异性,从而达到了降低离心泵内部流动诱导噪声的目的。刘厚林等[11]为预测离心泵在不同流量工况下叶片偶极子声源所产生的流动诱噪声的规律,通过计算叶片偶极子声源,得到了叶片偶极子声源下的叶片及其谐频的声压分布。袁寿其、司乔瑞等[12]为描述泵内部流动诱导噪声,基于Lighthill声类比理论,通过计算流体力学和计算声学两种软件进行计算分析,结果发现,流动诱导噪声的主频主要分布在叶频及其倍频处。
前人关于泵内部压力脉动及其流动诱导噪声的研究主要集中在离心泵和蜗壳式混流泵上,而对轴流泵的研究相对较少。因此本文将以轴流泵模型为研究对象,通过对轴流泵进行非定常数值计算得到其内部流场的流动特性。在此基础上,基于CFD/CA理论,进一步研究了不同转速对轴流泵流动诱导噪声的影响,为轴流泵装置的高效、低噪和稳定运行提供指导。
1 数值计算模型及方法
本文以江苏某泵站立式轴流泵装置模型为研究对象,其主要设计参数如下:设计流量为Q=328.5 L/s,额定转速为1 461 r/min,叶轮叶片数为4,导叶数为7,模型叶轮直径为300 mm,叶片安放角为0°。
图1为轴流泵装置计算域。计算域包括弯肘型进水流道、叶轮、导叶体及虹吸式出水流道4部分。
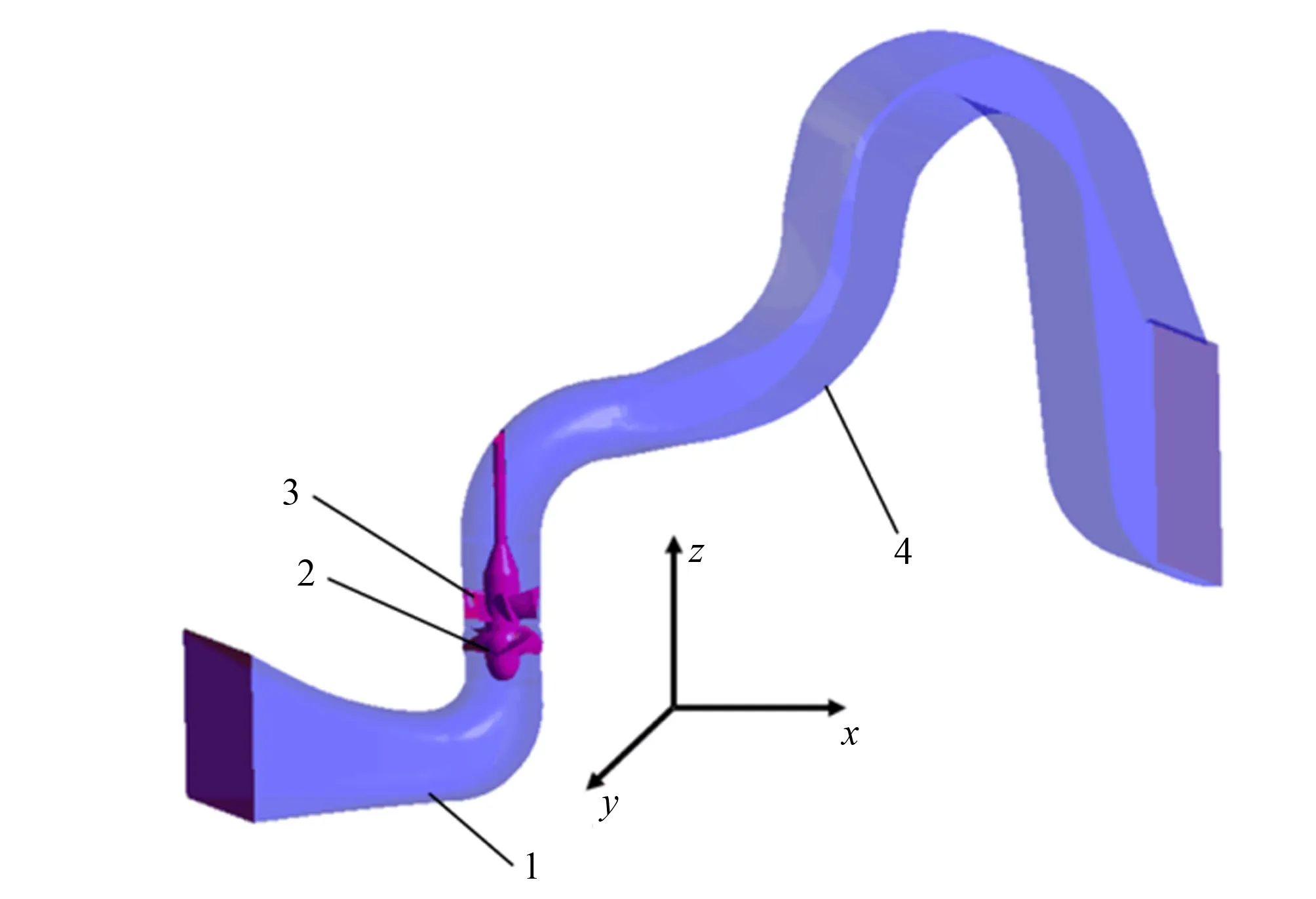
1-弯肘型进水流道;2-叶轮;3-导叶体;4-虹吸式出水流道图1 轴流泵装置计算域Fig.1 Calculation domain of axial-flow pump device
采用ICEM CFD软件对计算域进行网格划分,考虑到整个模型几何形状复杂且不规则,故采用适应性较强的非结构化网格。为提高数值模拟的准确性,对轴流泵的叶片和导叶部分进行局部加密。进行网格无关性验证,考虑到相同的收敛精度(10-5),网格数大于320 万个时,扬程的相对差值在1%以内,综合考虑计算精度与节省计算机资源,确定最终计算网格数为321 万个左右。
选择广泛应用于流体机械外特性预测的k-ε双方程湍流模型[13]。该模型考虑了紊动速度比尺和紊动长度比尺的输运,因而能精确地描述许多流动的物理过程,在流体机械中具有较好的通用性[14]。为了实现交界面上数据的传递,在定常计算时,将动静交界面设置为冻结转子类型;非定常计算时,将动静交界面设置为瞬态冻结转子类型。确定本次计算区域的进、出口为轴流泵装置进水流道的进口和出水流道的出口。进口采用质量流量边界条件,出口采用自由出流边界条件。在定常数值计算时,计算残差设置为10-5,同时对扬程和效率设置监测点。当扬程、效率的监测曲线趋于稳定且残差值满足设置的精度时,认为计算满足要求。在定常计算结果的基础上,对轴流泵装置模型在1 461 r/min(n)、1 315 r/min(0.9n)、1 169 r/min(0.8n)3组转速下进行三维非定常数值计算。设置的时间步长为(1/120)T,共计算18个周期,因此不同转速采用了不同的时间步长与计算时间,其具体参数见表1。

表1 时间步长和总的计算时间Tab.1 Time step and total calculation time
为充分研究不同转速下轴流泵内部的压力脉动特性,在叶轮进口处,叶轮出口处和导叶出口处3个不同截面处,分别从轮毂到轮缘布置了4个监测点,共12个监测点,如图2所示,以此来监测轴流泵内部不同部位的压力脉动情况。
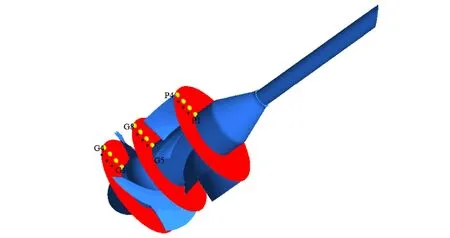
图2 轴流泵内部监测点设置Fig.2 Monitoring point Settings inside the axial-flow pump
2 数值计算结果分析
通过数值计算得到了轴流泵内部各监测点的压力脉动时域信息,定义一个无量纲压力脉动系数Cp来描述各监测点的压力脉动特性,其表达式为:
(1)
式中:Cp为无量纲压力系数,其便于将不同工况下的压力脉动进行分析比较;Pi为监测点在某一时刻的静压值,Pa;Pavc为各监测点在一个转动周期内静压的平均值,Pa。
2.1 设计转速下压力脉动分析
图3是在设计转速下轴流泵叶轮进口处压力脉动时域及频域图。通过下图分析可以看出,叶轮进口处压力脉动在设计流量工况下具有较好的周期性;同一组监测点,其压力脉动幅值呈现出从轮缘至轮毂逐渐减小的趋势;压力脉动主频为4倍转频,其值与转轮通过频率一致;次主频为192 Hz,为8倍的转频;说明转轮的转动对叶轮进口的压力脉动具有重要的影响。
图4是在设计转速下轴流泵叶轮出口处压力脉动时域及频域特性图。在设计工况下叶轮出口处压力脉动周期性相对较差;同一组监测点,其压力脉动幅值依旧呈现出从轮缘至轮毂逐渐减小的趋势,对应的压力脉动主频为7倍转频,其值与导叶通过频率一致,说明导叶对叶轮出口的压力脉动也产生了重要的影响。
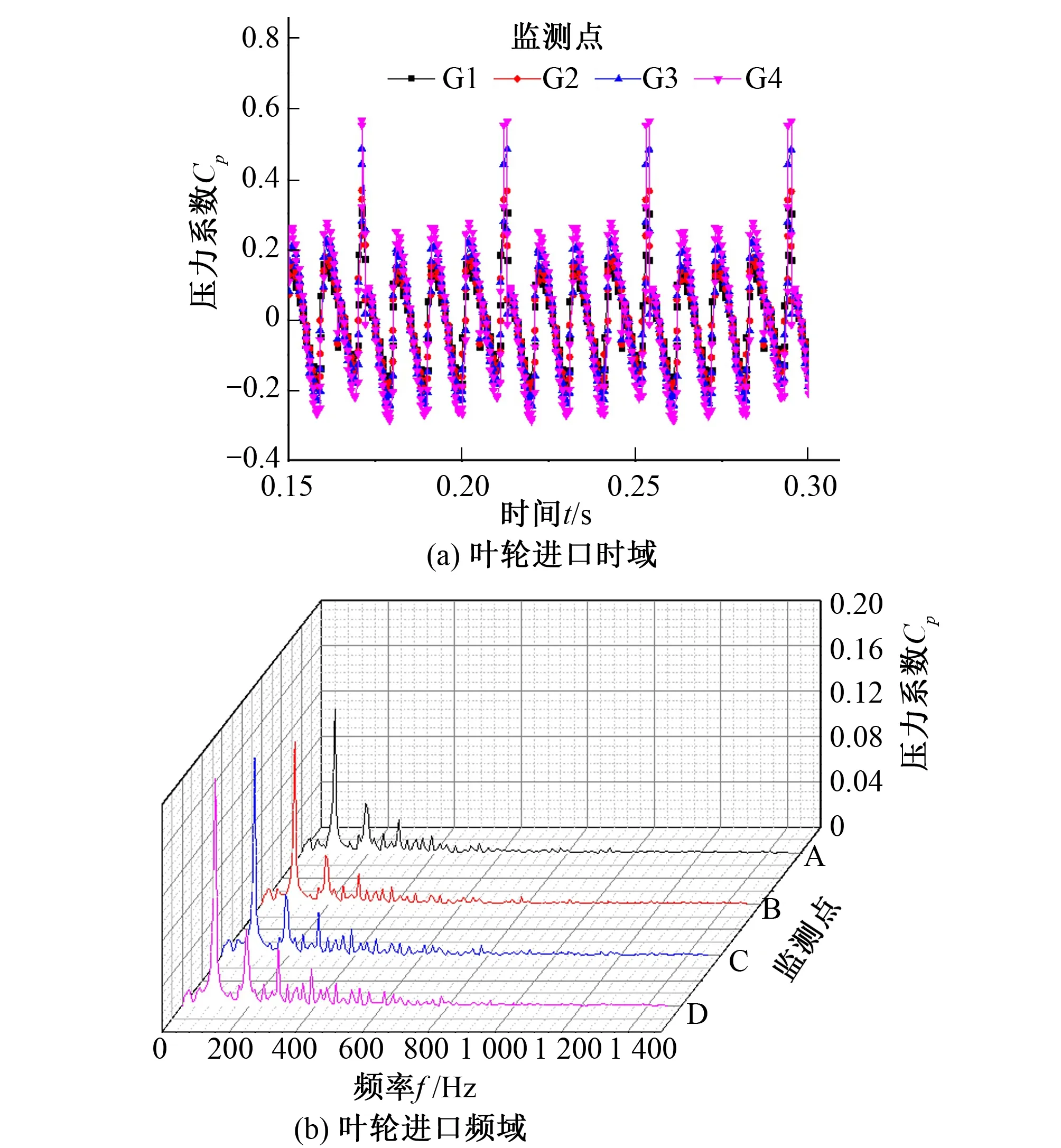
图3 转速为1 461 r/min时,叶轮进口压力脉动Fig.3 Pressure pulsation at impeller inlet when the rotating speed is 1 461 r/min
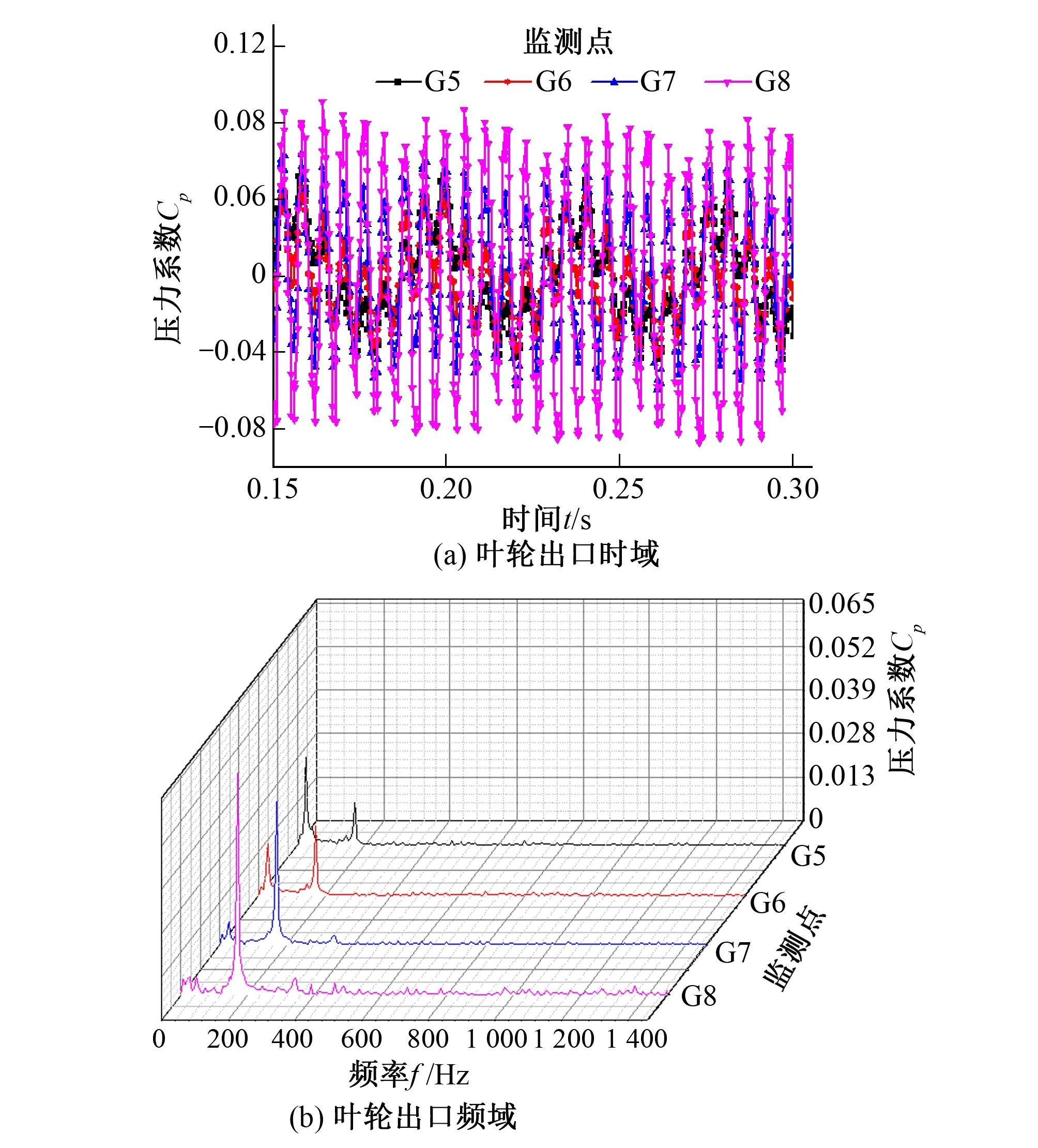
图4 转速为1 461 r/min时,叶轮出口压力脉动Fig.4 Pressure pulsation at the impeller outlet when the rotating speed is 1 461 r/min
图5是在设计转速下轴流泵导叶出口处压力脉动时域及频域特性图。在设计工况下导叶出口处压力脉动具有较好的周期性;相比叶轮进口及叶轮出口处,导叶出口处压力脉动幅值较小,说明导叶的存在抑制了泵内的压力脉动幅值;导叶出口处的压力脉动幅值与叶轮进、出口脉动幅值变化规律一致,也为从轮缘至轮毂逐渐递减的规律,且压力脉动在1倍的转频及4倍转频处具有较大幅值。

图5 转速为1 461 r/min时,导叶出口压力脉动Fig.5 Pressure pulsation at guide vane outlet at rotation speed of 1 461 r/min
2.2 非设计转速下压力脉动分析
(1)1 315 r/min压力脉动。图6是转速为1 315 r/min时,轴流泵装置在上述3组监测点处的压力脉动时域图及频域图。在该转速下叶轮进口及导叶出口处压力脉动也呈现出较好的周期性;叶轮进口处压力脉动在4倍转频和8倍转频处具有较大的幅值,其压力脉动系数幅值约为设计转速下的0.65倍;叶轮出口的压力脉动主频为7倍转频,其压力脉动系数幅值约为设计转速下的0.81倍;导叶出口处的压力脉动在1倍及4倍转频处具有较大幅值。
图7是转速为1 169 r/min时轴流泵装置在上述3组监测点处的压力脉动时域图及频域图。在该转速下叶轮进口处及导叶出口处压力脉动依然具有较好的周期性。叶轮进口处的压力脉动在4倍转频及8倍转频处具有较大的幅值;其压力脉动系数幅值约为设计转速下的0.57倍;叶轮出口的压力脉动主频为7倍转频,其压力脉动系数幅值约为设计转速下的0.68倍;导叶出口处的压力脉动在1倍及4倍转频处具有较大幅值。

图6 转速为1 315 r/min时,轴流泵内部压力脉动Fig.6 Pressure pulsation inside the axial flow pump at 1 315 r/min

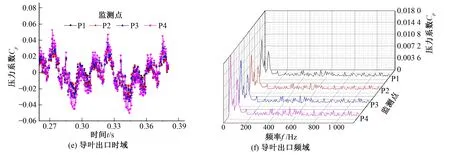
图7 转速为1 169 r/min时,轴流泵内部压力脉动Fig.7 Pressure pulsation inside the axial flow pump at a rotational speed of 1 169 r/min
2.3 声学数值计算结果与分析
为更直观地了解轴流泵流动诱导噪声的指向性分布和噪声声压级分布,以轴流泵叶轮的旋转中心为圆心,分别在XY面,XZ面和YZ面上建立半径为2 m的声学监测面,并在距离圆心为1 m的圆周上,每隔15°布置一个监测点,每个面上共布置24个监测点。如图8所示。
由于篇幅限制,本文只对一阶及三阶叶频处的噪声声压级分布及指向性分布进行分析。
图9为在3组转速n(1 461 r/min)、0.9n(1 315 r/min)、0.8n(1 169 r/min),其相对应设计流量分别为328.5、296.7、262.8 L/s下,在叶片旋转偶极子声源作用下,在XZ监测面上

图8 声场监测面布置Fig.8 Layout of noise field monitoring surface
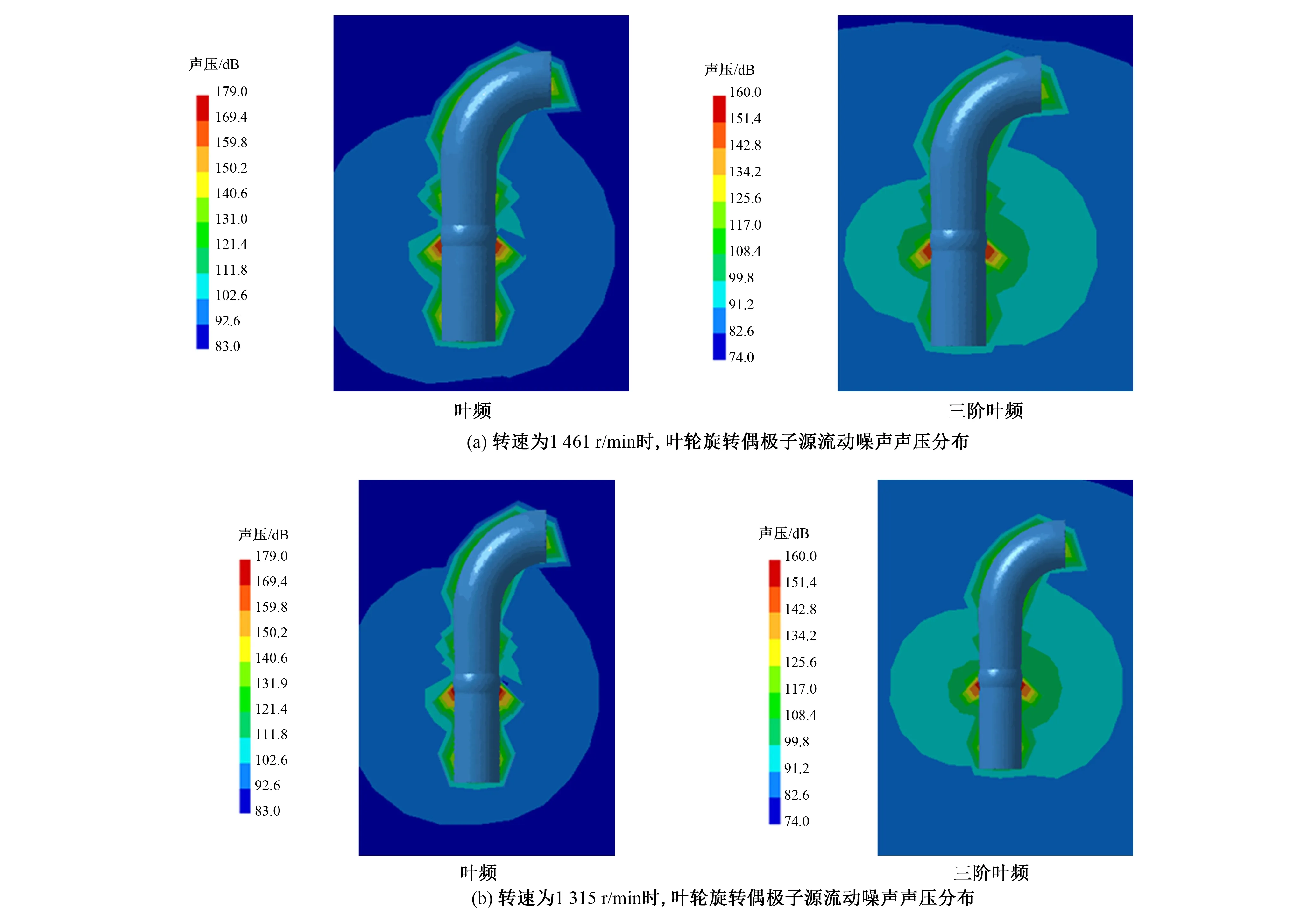

图9 3组不同转速下,XZ监测面上叶频和三阶叶频处的外场声压级分布Fig.9 Sound pressure level distribution at blade frequency and third-order blade frequency on the XZ monitoring surface at three groups of different rotational speeds
的叶频和三阶叶频处的外场声压分布。
从图9可以看出,转速为1 461 r/min时,在XZ面上,叶片旋转偶极子作用下辐射的声场分布与轴流泵的几何轮廓十分吻合;在转轮室周围辐射的声压级较大,随着场点离泵体越远,其声压值也随之降低;叶频处的声压级较三阶叶频处的声压级大,分析其原因可能是该值与泵体结构的固有频率值一致,因此轴流泵内的流体与泵壳之间发生共振,从而加剧了噪声声压级与辐射水平。
与转速为1 461 r/min时的叶轮旋转偶极子源流动噪声声压分布相比, 1 315和1 161 r/min两种转速下的声压分布与其类似。同样地,在XZ面上,叶片旋转偶极子作用下辐射出的声场的分布与轴流泵的几何轮廓十分吻合;在转轮室周围辐射的声压级较大,且随着转速的降低,其声压值也随之降低。
图10为3种转速下叶频及三阶叶频在XZ面上的流动诱导噪声指向性分布,其中纵坐标为声压级,单位dB;周向坐标为角度。
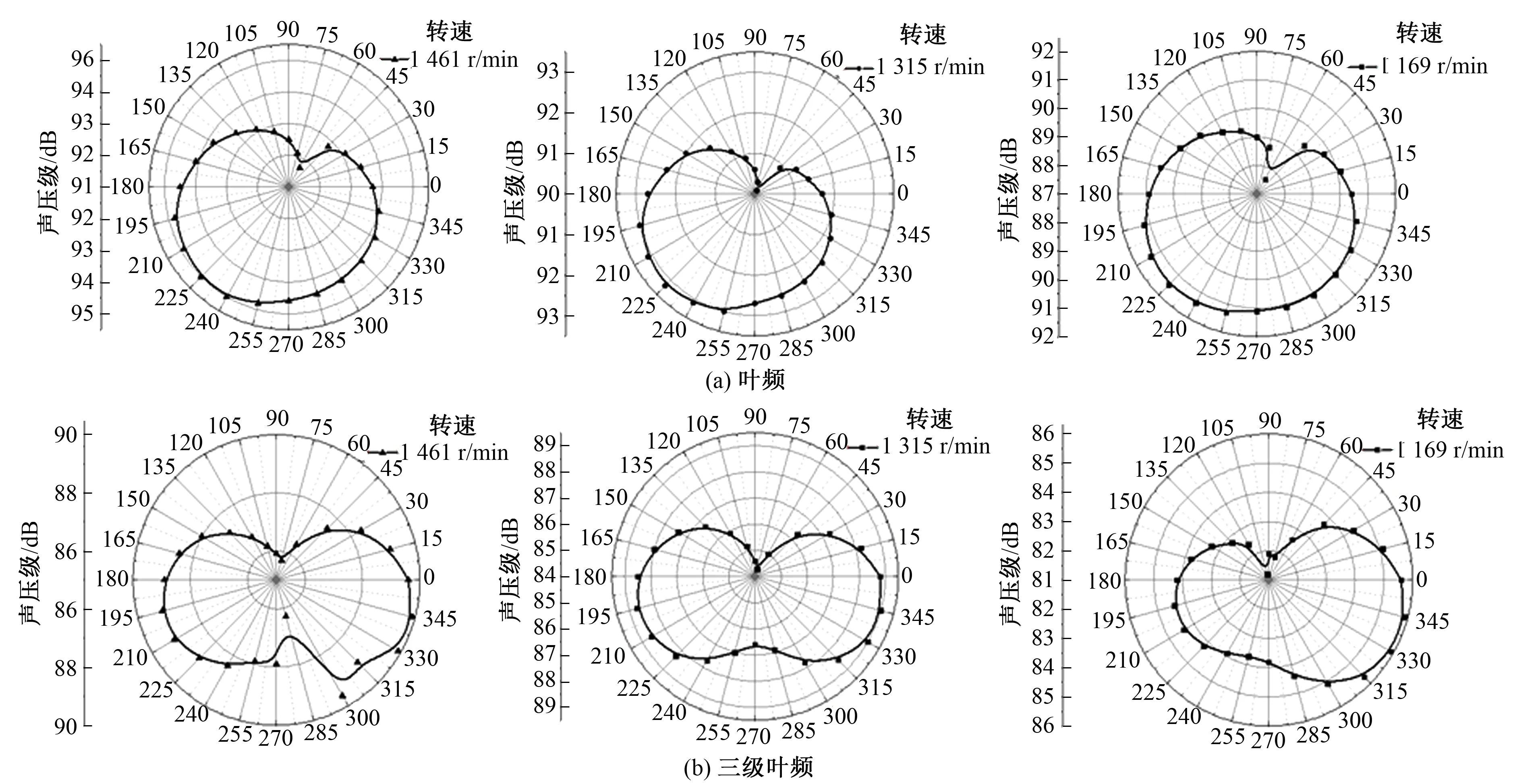
图10 XZ面上流动噪声指向性分布Fig.10 Directivity distribution of flow noise on XZ plane
从图10可以看出,转速对于外场声压的指向性形状基本无影响,但是随着转速的减小,辐射声场的声压级也会逐渐减小。在XZ面上,叶频处三组转速在60°附近位置声压级较小,在三阶叶频处呈现出偶极子辐射特性,在1 461和1 315 r/min下,呈现出明显的∞形偶极子特性,1 169 r/min指向也较明显。
综上所述:转速较高时,噪声辐射能力也越强;转速降低时,噪声辐射能力较高转速时具有较小的声压级。这与上文中分析的压力脉动具有相同的规律,即轴流泵内压力脉动随着转速的降低也逐渐减小,说明噪声辐射水平与泵内压力脉动幅值具有密切的关系。因此在对轴流泵内部流动诱导噪声研究前进行压力脉动的计算分析是必要的。
3 结 论
(1)通过对轴流泵进行非定常数值计算,结果表明:压力脉动主频与其转速、叶片数及导叶数有关;且不同转速下,其压力脉动主频基本保持一致;随着转速的降低,压力脉动幅值逐渐减小。
(2)不同转速下,叶轮出口处的监测点压力脉动幅值均较大,说明轴流泵内部的叶轮与导叶之间的动静干涉作用是引起压力脉动的重要原因;导叶出口处压力脉动幅值明显减小,说明导叶对泵内部压力脉动起到了减弱的作用。
(3)对比分析了3组转速下,叶频及三阶叶频处叶片旋转偶极子声源作用下在XZ监测平面上的外场声压级分布,结果表明:转速对于外场声压的指向性形状基本无影响;随着转速的减小,辐射声场的声压级也逐渐减小,这与上文分析的压力脉动具有相同的规律,说明了噪声辐射水平与泵内压力脉动幅值具有密切的关系,研究轴流泵内部压力脉动特性对于流动诱导噪声的控制具有指导作用。

