基于VMD的甩负荷试验尾水管压力分析及预测

曹林宁，蒋 磊，陈忠宾，倪海梅

(1.河海大学能源与电气学院，南京 210098；2.江苏国信溧阳抽水蓄能发电有限公司，江苏 溧阳 213300)

0 引 言

机组甩负荷试验[1-4]是抽水蓄能电站正常投运前的考核之一，是检验主机、调速器、励磁系统最重要的试验项目。对于多台机组共用引水及尾水系统的水电站，现场甩负荷试验遵循从单机到多机、从甩部分负荷到全部负荷的顺序。机组在并网正常运行时发电机出口断路器突然断开，输出的电磁力矩为零，转动力矩将使机组转速持续升高，抑制转速升高则需要导叶快速关闭，水流状态的剧烈变化引起输水管道中巨大的水锤压力，而水流冲击各过流部件又会产生巨大的脉动，导致现场实测压力数据信息混乱[5, 6]。转速的测量信号表达比较直观，为了提取压力信号中的有用信息，钭锦周、王卫玉[7]等人基于自相关系数将EMD分解出的本征模态函数分成信号主导分量及噪声主导分量，对噪声主导分量进行小波软阈值降噪处理后重构信号；于晓东、潘罗平[8]基于变分模态分解和排列熵法完成了对水轮机脉动信号的去噪，相对于经验模态分解提高了重构后信号与原始信号的相关性；王翰、罗兴锜[9]等人采用经验模态分解和指标能量结合方法对尾水管动态信号进行了模式识别，分析了复杂而特殊的水轮机动态特征信息；杨桀彬、杨建东[10]等人利用模型试验脉动压力等值线图并结合甩负荷工况轨迹线图模拟出脉动压力幅值，较准确地预测出过渡过程中的总动水压力。

本文基于VMD算法对真机甩负荷试验数据进行分解，提取尾水管进口水压力的趋势项和脉动项，对不同工况下的脉动项进行频谱分析，结合一维计算对一管多机满出力同时甩全负荷时的尾水管进口总压力进行预测。

1 VMD算法数据分解准则

VMD算法是Dragomiretskiy等人提出的一种非平稳信号分解算法[11-13]，分解出的模态函数定义为调幅调频信号uk(t)=Ak(t)cos[φk(t)]，算法迭代流程如下：

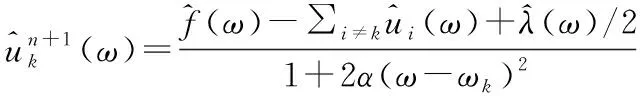
VMD算法基于严格的数学理论推导且具有良好的自适应性，算法定义分解出的每个本征模态函数(IMF)都有一个明确的中心频带。现场甩负荷试验水压力波动由流量变化引起的水锤压力与不同激励引起的脉动压力组成[14, 15]，水锤压力表现为频率为零的均值压力，脉动压力通过主频大小确定能量来源。算法本身通过中心频带分解非平稳信号的方法应用于甩负荷试验压力数据是可行的。信号分解需输入模态数K值，本文采用预分解法确定K值：预先设定合适的K值为N，观测分解所得各IMF中心频率是否重叠，若重叠则说明出现过分解，此时取K=N-1；若并未发生重叠则说明欠分解，此时取K=N+1，继续对原始数据进行分解，直至得到满足条件的K值。

2 实例分析

2.1 甩负荷试验尾水管进口压力分解

本文借用某抽水蓄能电站现场甩负荷试验进行数据分析。电站输水系统平面布置见图1，基本参数见表1。

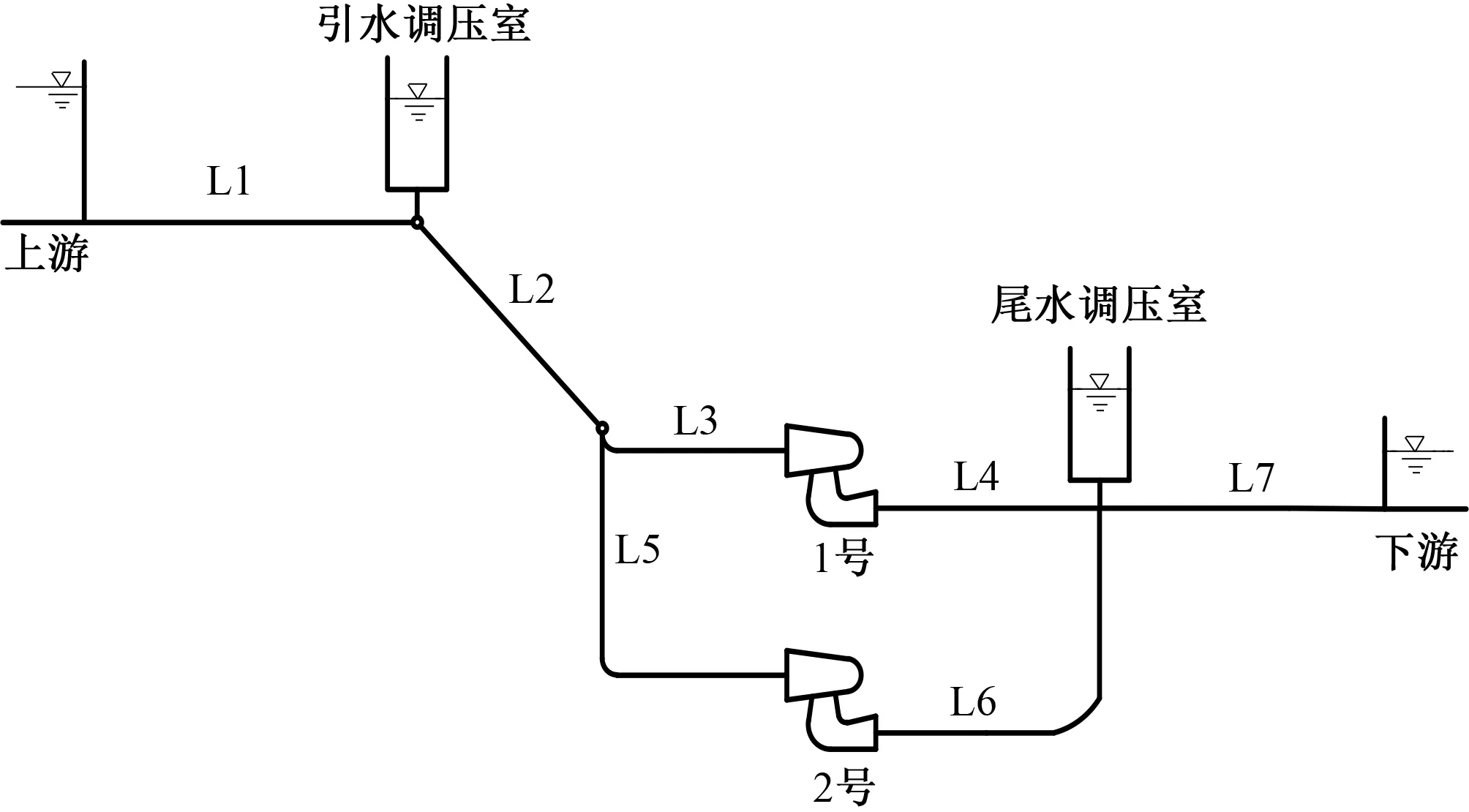
图1 某抽水蓄能电站布置图Fig.1 Schematic diagram of pumped storage power station

本电站过渡过程保证值：

表1 电站基本参数表Tab.1 Basic parameters of power station

(1)蜗壳进口处最大压力水头值不大于580 m；

(2)水泵水轮机最大转速上升值不大于40%；

(3)尾水管进口处的最小压力水头值不小于10 m。

现场依次采用单机25%、50%、75%、100% 4个负荷点和一管双机25%、50%、75%、100% 4个负荷点进行试验。压力传感器的采样频率为1 200 Hz，在试验前对传感器引出的测量管道进行了排气处理，减小干扰信号引起的测量误差。选取4个甩负荷工况进行分析，见表2，其中一管双机满出力同时甩全负荷为待预测工况。

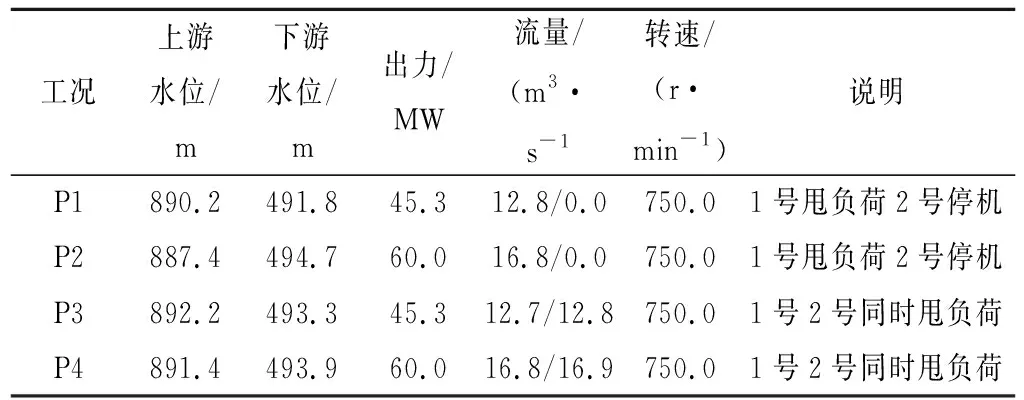
表2 甩负荷工况表Table 2. Load rejection condition table

以P1工况为例，算法将实测尾水管进口压力分为两个模态函数见图2，IMF1对应的频带中心频率接近于0，则提取IMF1为均值压力，从总压力中减去均值压力提取为脉动压力。3个工况尾水管进口实测压力经过特征提取后的压力波动信号见图3。

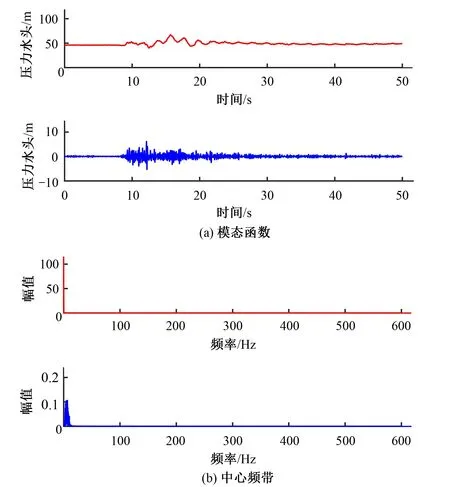
图2 P1工况尾水管进口压力分解图Fig.2 Decomposition diagram of inlet pressure of draft tube in P1 working condition

图3 脉动压力特征提取图Fig.3 Feature extraction diagram of pulsating pressure

由图3可以看出，边界条件一定时，单机甩全负荷脉动压力幅值大于单机甩部分负荷脉动压力幅值，双机同时甩负荷脉动压力幅值大于单机甩同等负荷脉动压力幅值。

2.2 尾水管进口压力脉动项频谱分析

通过转速变化曲线确定甩负荷开始时刻，同时引入无量纲参数H表示脉动压力，消除水头变化带来的影响，截取原始数据长度40 s进行时域分析见图4。

(1)

式中：γ是水的重度，值为9 810 N/m3；Hg为不同工况下水电站毛水头。

图4 P1、P2、P3工况转速变化与脉动压力图Fig.4 Diagram of rotation speed change and pulsating pressure in P1, P2 and P3 working conditions

由图4可以看出转速变化曲线到达第一个波峰，此时机组到达飞逸进入制动区，脉动压力幅值增大到最大；随着转速降低，脉动幅值急剧减小；转速变化曲线到达第二个波峰，脉动压力幅值也增大到峰值，即脉动压力幅值呈现与转速相近的变化趋势。

混流式水泵水轮机的压力脉动来源主要是高频的动静干涉、低频的旋转失速以及尾水涡带，其对应频率如表3所示。

表3 混流式水泵水轮机压力脉动成分表Tab.3 Francis pump turbine pressure fluctuation composition table

为了识别尾水管进口脉动压力激励源，对3个工况分解所得脉动压力进行傅里叶变换，结果见图5。

由图5(d)可以读出3个工况尾水管进口脉动压力主频依次为4.6、6.4和24.9 Hz，通过时频图找到对应工况主频发生时刻，由图4转速变化图读取对应时刻机组转速并换算为机组转频依次为15.1、12.8和14.3 Hz，即3个工况的尾水管进口脉动压力主频依次为对应时刻机组转频的0.3、0.5和1.7倍，数据表明尾水管进口脉动压力主要集中在低于30 Hz的频段，高频段的动静干涉未对甩负荷过程中的尾水管进口脉动压力产生影响。

2.3 尾水管进口总压力预测

为防止现场甩负荷试验尾水管进口出现水柱分离现象，需要在试验之前对一管多机满出力同时甩全负荷工况进行压力预测。工程上主要计算机组在过渡过程压力波动曲线极值是否满足保证值要求。本电站P1、P2、P3为已测工况，P4为待测工况。基于特征线法的P4工况一维数值仿真结果见图6。

由于特征线法采用弹性水击数学模型忽略了脉动压力的影响，图6所示的尾水管进口压力曲线非常光滑，与现场实测试验数据并不吻合。在提取了P1、P2、P3工况尾水管进口脉动压力基础上，本文从两个方向分别反演计算P4工况尾水管进口总压力。P4工况尾水管进口总压力预测由均值压力与脉动压力组成如公式(2)所示。

P4总=P4均值+P4脉动

(2)

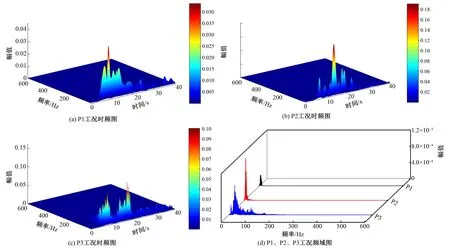
图5 P1、P2、P3工况脉动压力时频图Fig.5 Time-frequency diagram of pulsating pressure in P1, P2 and P3 working conditions

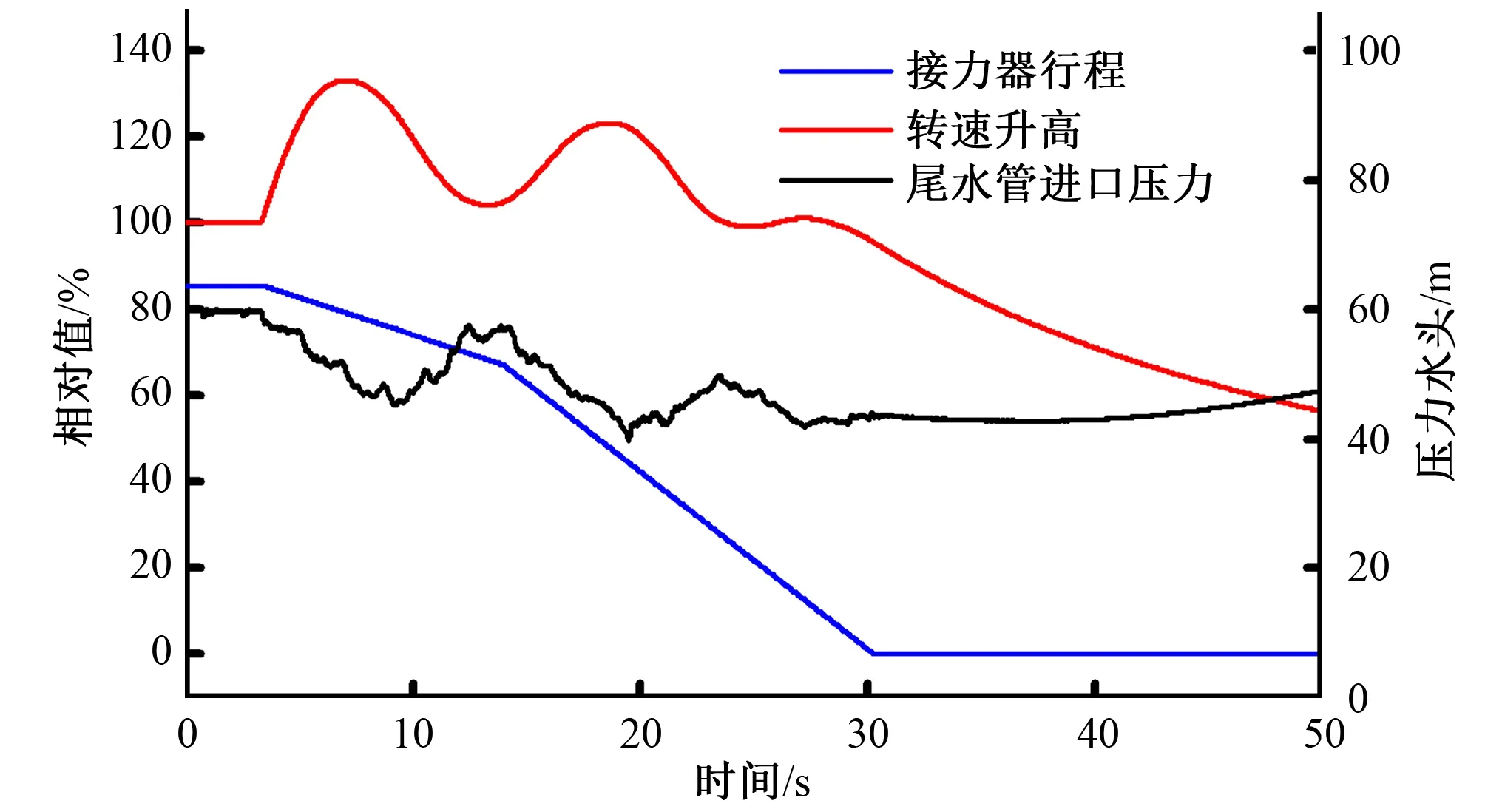
图6 一维数值仿真计算结果图Fig.6 Results of one-dimensional numerical simulation

其中均值压力基于特征线法一维数值计算，脉动压力分别由P2和P3工况分解所得。在统一了一维仿真计算步长与现场数据采样频率之后，预测得到的P4工况尾水管进口总动水压力如图7所示。

由图7可以看出：P3工况反演计算P4工况相对于P2工况反演计算更好地拟合实测数据，其尾水管进口预测总压力波动与现场实测数据在5～20 s吻合较好，0～5 s的初始静水压力相差较大，在20～40 s内预测结果水流波动比实测结果收敛更迅速。

分别提取P4工况尾水管进口一维计算均值压力、两种方案预测总压力、实测总压力曲线的极小值如表4所示。

表4 尾水管进口压力极值对比表Tab.4 Extreme value comparison of inlet water pressure of draft tube

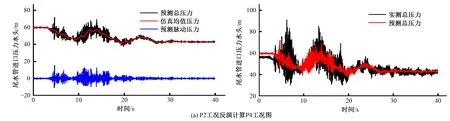
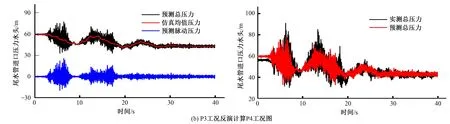
图7 P4工况预测总压力与实测总压力对比图Fig.7 P4 comparison diagram of the predicted total pressure and the measured total pressur

数据表明P4工况尾水管进口一维计算均值压力与预测总压力水头结果均大于10 m，满足过渡过程调节保证值；均值压力加上脉动压力的总动水压力预测结果更接近于实测结果；双机75%负荷点预测双机100%负荷点比单机100%负荷点预测双机100%负荷点更准确。

3 结 语

本文基于VMD算法提取甩负荷过程尾水管进口实测数据的脉动压力，并结合一维特征线法对双机甩满负荷工况进行了压力预测，结果表明：

(1)VMD算法基于中心频带分解非平稳信号的方法能够应用于甩负荷试验，现场实测压力分解得到的第一阶模态函数即表现为频率为零的均值压力。

(2)甩负荷过程尾水管进口脉动压力幅值在机组制动区达到最大，整体呈现与机组转速变化相近的趋势；脉动压力成分集中在低频段，高频段的动静干涉未产生影响。

(3)相对于一维仿真，均值压力结合脉动压力的反演计算能够更好地模拟出现场甩负荷试验过程,同时在保证现场试验边界条件一致情况下，双机到双机的反演计算比单机到双机的反演计算更为准确，为水电站相关工程应用提供一定参考。