渠系水利用系数测算方法研究

谢亨旺，罗云英，靳伟荣

(1.江西省灌溉试验中心站，南昌 330201；2. 暨南大学环境学院，广州 511443；3.武汉大学水利水电学院，武汉 430072)

0 引 言

灌溉水有效利用系数是最严格水资源管理的指标之一，也是农业灌溉用水管理、灌溉技术水平评价、区域水资源配置和制定节水灌溉发展规划的基础参数[1]。渠系水利用系数是灌溉水有效利用系数的重要组成部分，其测算方法的研究有助于正确认识灌溉水利用系数指标及内涵。目前测算渠系水利用系数国外常用的经验公式有Davis-Wilson公式、USBR公式、Ingham公式、Molesworth公式、前苏联公式和Kositiakov经验公式等[2,3]。我国广泛采用Kositiakov经验公式的改进公式[4]，对土壤透水性能经验常数做了细化规定，但由于各地区普遍缺少渠道状况的实测参数资料，使该公式在实际应用中存在较多问题。荣丰涛、江崇安等分析了现行渠道渗漏量计算方法的不足，如渗水量减少系数、防渗材料渗透系数等难以确定[5,6]；门宝辉、钟玲等利用积分方法推导了新公式，对传统渠道损失流量计算公式的不足进行了修正，提高了渠道损失流量和渠道水利用系数的计算精度[7,8]；白美健等采用回归分析方法建立了渠道渗漏损失水量与流量间的相关关系，总结出了依据渠道流量估算渠道水利用系数的经验公式[9]。本文应用渠道连续渗漏理论，对传统计算渠道单位长度入渗损失系数的Kostiakov经验公式进行改进，并在江西省赣抚平原灌区进行验证。改进的计算方法将渠道流量损失过程看成水在沿渠道流动方向的连续动态过程，符合水流损失规律，但相关计算精度仍然受到防渗渠道损失修正系数、地下水顶托修正系数等参数的影响。这些数据需要大量的试验资料进行率定。

1 国内常用的Kostiakov经验公式及其改进

1.1 国内常用的Kostiakov经验公式

我国在计算渠道渗漏损失的时候多以Kostiakov经验公式为基础，并对反映土壤透水性能的经验常数A、m进行了细化，也考虑了渠道衬砌方式及地下水位对渠道渗水损失的影响。常用的的经验公式形式为：

σ=0.01AQ-m

(1)

S=0.01γβAQ1-m

(2)

式中：σ为每公里渠道输水损失率，%；Q为渠道流量，m3/s；A、m为渠床土壤透水参数；S为每公里渠道的渠道输水损失流量，m3/s；σ为地下水顶托修正系数；β为采取防渗措施后渠道渗水损失修正系数。

在《灌溉与排水工程设计规范》(GB 50288-99)和《农田水利学》[4]中，式(2)中的A、m、γ、β的取值分别见表1、表2和表3。

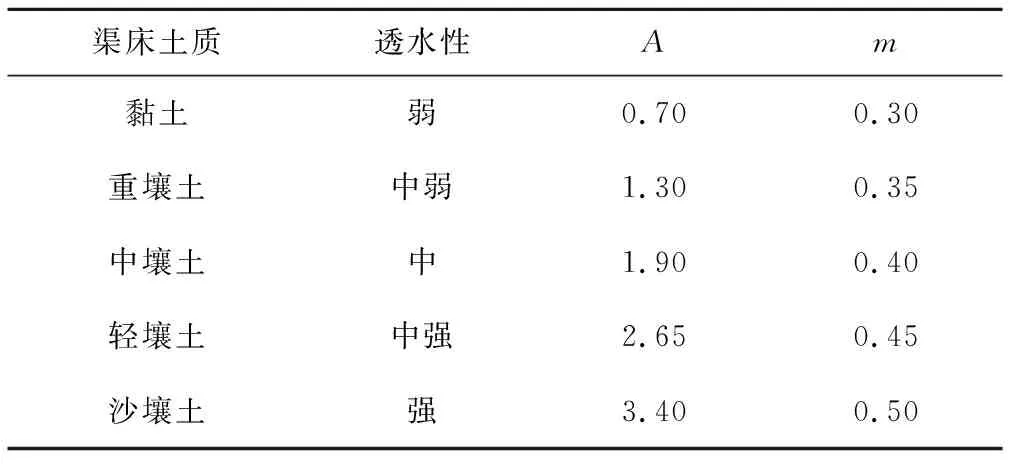
表1 Kostiakov公式土壤透水参数A、m

表2 地下水顶托修正系数γ

表3 采取防渗措施渠道渗水损失修正系数β经验取值

已知某类型渠道的长度 (单位：km)、渠道毛流量为Qg、渠道净流量为Qn。当灌区地下水位较高时，地下水壅阻会减少渠道渗漏，用系数γ修正；当渠道采取了防渗措施时，不同防渗措施会对渠道渗水产生不同程度的降低折减，用系数β进行修正。综合考虑地下水和防渗措施的影响，渠道渗漏水量可按下式计算：

ΔQ=βγσLQn

(3)

该段渠道的渠道水利用系数为：

(4)

1.2 Kostiakov经验公式的改进

Kostiakov经验公式计算简便，在我国应用广泛，但它还存在一些明显的不足和局限性。作为估算公式，其估算精度取决于参数A、m、γ、β的取值是否合理。单位渠道输水损失率σ是渠道流量的函数，而渠道流量沿程变化，一般按式(3)～(4)计算时，假定了σ不随沿程渠道流量变化而变化，这使得计算渠道越长误差越大。李淑荣通过论述多种求解渠系水利用系数思路，探索推导出利用系数法、损失系数法及定义法的误差公式，在此基础上揭示了误差产生的原因，损失系数法在计算过程中忽略了沿程渠道流量变化[10]。

荣丰涛分析了Kostiakov经验公式未考虑渠道长度对计算结果的影响，用现行公式计算了渠道渗漏损失相对误差小于5%时的最大允许计算渠长，结果表明，在A、m、β一定的情况下，最大允许渠长随着设计流量Q的增加而增加；在其他参数不变的情况下，渠道防渗效果越好(β越小)，最大允许渠长越长[5]。

根据公式(2)可以发现，Kostiakov经验公式求得的每公里渠长的输水损失是一样的，而实际上每公里渠长上的损失流量随流量变化，越往渠尾处流量越小，相应的渗水损失也越小，渠首段单位渠长的流量损失一般大于渠尾段。针对这种情况，门登辉等学者提出采用积分方法对渠道设计中的流量损失计算公式进行改进[7-9]。设渠首毛流量为Qg，经过流程L后净流量为Qn。设渠道流量Q在经过渠段dl后的损失流量为dQ。在dl渠段内，单位流量在单位流程上的损失σ=dQ/(Qdl)，则：

(5)

将上式(5)在渠长L范围内进行积分求解得：

(6)

(7)

(8)

该计算公式将渠道流量损失过程看成水在沿渠道流动方向的连续动态过程，符合水流损失规律，会显著提高估算精度。

2 改进公式的应用效果

将改进的公式与一般使用的Kostiakov经验公式进行比较分析，求解不同情况下的相对误差，相对误差 用下式进行表示：

(9)

式中：ΔQ改进为积分方法改进公式推求的渠道流量损失值，m3/s；ΔQ为Kostiakov公式推求的渠道流量损失的近似值，m3/s。

取A=1.9、m=0.4，不考虑顶托和渠道防渗衬砌措施。分别采用Kostiakov经验公式和积分方法改进的公式计算不同流量和渠长组合情况下的渠道输水损失量，计算结果见表4。

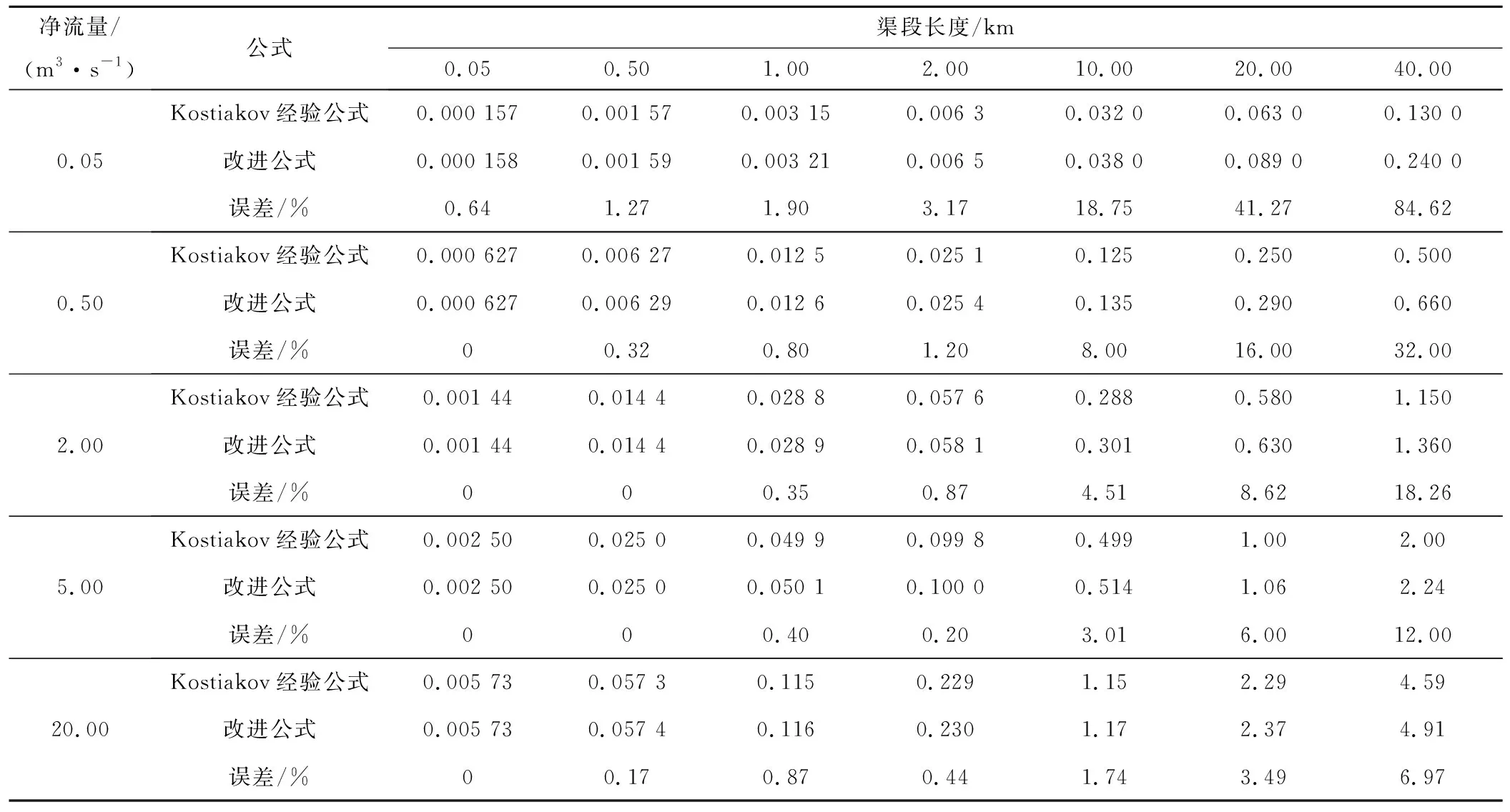
表4 改进前后渠道损失流量对比

由表4可知，2种公式损失流量的计算结果均与渠道净流量和渠道长度有关，无论是Kostiakov经验公式计算还是积分改进公式计算，渠道流量和长度均与渠道损失流量成正相关关系。渠道净流量一定时，2种方法的计算结果在较小的渠道长度范围内，相对误差很小，计算结果都可以为工程采用。但是随着渠道长度的增加，Kostiakov经验公式计算结果与积分改进公式计算结果的相对误差逐渐增大。

3 改进经验公式在灌区进行验证

3.1 改进经验公式与实测数据比较分析

本文采用动水测定法的实测数据对经验公式的适用性进行验证。

实际测定工作在位于江西省赣抚平原灌区二干渠上进行。选择二干二支渠、五支渠为典型支渠，二支三斗渠、五支五斗渠为典型斗渠，典型支、斗渠所处位置见图1、图2。对于二支三斗渠，根据《基本农田建设设计规范》布置20条农渠，受地形限制，每条农渠的灌溉面积不尽相等；根据农渠控制灌溉面积大致相等分2组轮灌(三斗渠上左、右前6条农渠为第1轮灌组，7～10条为第2轮灌组)，渠系概化图见图1。在五支五斗渠上布置了20条农渠，分2组轮灌(斗渠上左、右1～5条农渠为一组，6～10为一组)，渠系分布情况见概化图图2。

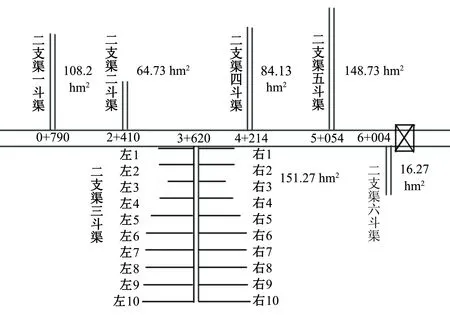
图1 二干渠二支渠概化图

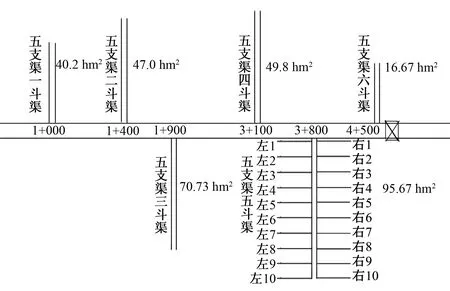
图2 二干渠五支渠概化图

根据实地调查，研究区干渠、支渠全部为混凝土衬砌，斗渠、农渠一半为衬砌渠道一半为土渠，斗渠防渗形式为混凝土护面，农渠为U形槽。计算衬砌渠道时，假设衬砌优先从渠首位置开始。采取防渗措施的各级渠道都采用混凝土材料，参考表3可知，混凝土护面的衬砌折减系数β为0.05～0.15。本文在计算过程中，对采用防渗措施的干渠和支渠的β取中间值0.1；由于斗渠和农渠衬砌厚度较薄且日常维护较少，所以取相应的衬砌渠道β值为0.15。二干渠灌溉区域的渠道工作制度为干渠、支渠、斗渠续灌，农渠轮灌。

3.1.1 农渠渠道水利用系数

采用田间水利用系数实测结果0.917 6推算农渠田间净流量：

(10)

式中：A农为农渠灌溉面积，万hm2；Q农净为农渠供给田间的净流量，m3/s；q设为设计净灌水率，m3/(s·hm2)。

根据公式(6)有：

(11)

式中：Q农净为农渠的净流量，m3/s；Q农毛为农渠的毛流量，m3/s；研究区域土质为轻壤土，参考表1，取A=2.65，m=0.45。

由Cropwat 8.0软件计算得到研究区域1951-2013年腾发量ET，进而推求作物灌溉制度和灌溉定额，根据种植比例求得研究区年灌溉用水定额，由1963年灌溉用水定额排频绘制P-Ⅲ曲线，得灌溉用水保证率为90%时设计典型年为1966年，绘制灌水率图并修正，得设计净灌水率为0.000 705 m3/(s·hm2)。

根据动水测定法计算得到的典型渠段上下游流量Q典1和Q典2，就可以求得典型渠段的水利用系数η典段：

η典段=Q典1/Q典2

(12)

动水测定法渠道输水损失系数改进公式为：

(13)

由公式(12)、(13)得每条农渠毛流量和渠道水利用系数，由控制灌溉面积加权平均得典型农渠平均渠道水利用系数为0.933，将其视为研究区域农渠渠道水利用系数，二支渠计算结果见表5。

3.1.2 斗渠渠道水利用系数

由于农渠轮灌，以农渠轮灌组最大流量值作为斗渠净流量，二支渠三斗渠结果见表5。

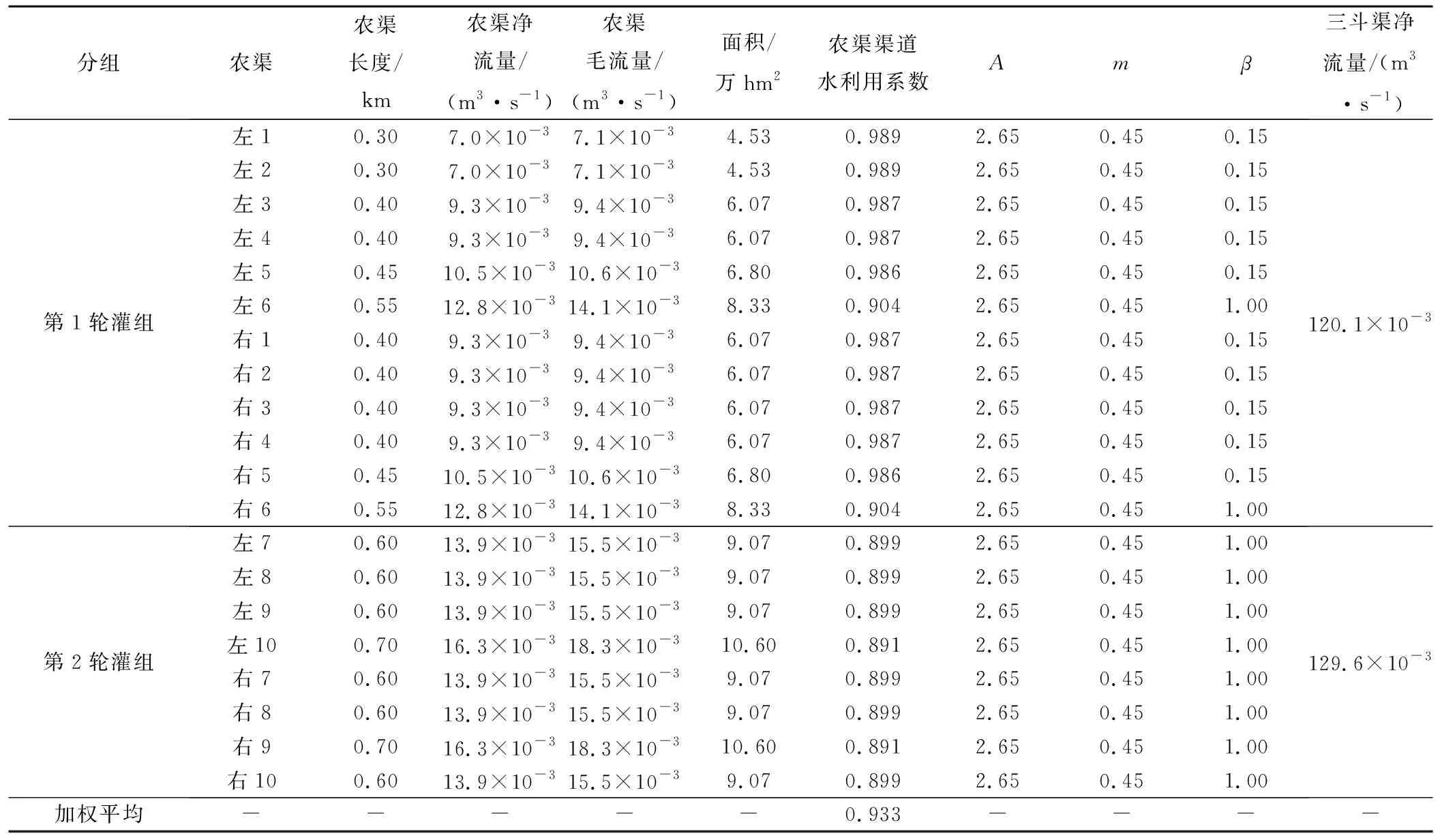
表5 二支渠农渠渠道水利用系数和三斗渠净流量计算结果

典型斗渠长度为1.68 km，自渠首起有一半长度采用混凝土材料衬砌，根据公式(6)得斗渠毛流量为0.134 3 m3/s，最终得到斗渠渠道水利用系数为0.964 6。以斗渠控制面积的灌溉水利用系数0.794为扩大指标来推求其他斗渠毛流量，进而得到二支渠净流量为0.509 2 m3/s，计算结果见表6。

表6 斗渠毛流量和支渠净流量计算结果

3.1.3 支渠渠道水利用系数。

典型支渠全部为混凝土材料衬砌，根据公式(12)求得支渠毛流量为0.516 8 m3/s，最终得到支渠渠道水利用系数为0.985 2，计算结果见表7。

表7 支渠毛流量计算结果

3.1.4 干渠渠道水利用系数

干渠全部为混凝土衬砌，以支渠控制面积的灌溉水利用系数0.782为扩大指标来推求其他支渠毛流量，进而得到二干渠净流量为8.683 6 m3/s，结果见表8。

求得二干渠的渠道水利用系数为0.984 3：

对于五支渠，同理推导得出各级渠道水利用系数，由面积加权平均得研究区域的各级渠道水利用系数和相应的渠系水利用系数，计算结果见表9。

此外，也可以由推算得到的净流量与毛流量的比值来计算渠系水利用系数(见表10)，二支渠和五支渠结果按面积加权平均后为0.839。

表8 二干渠流量推算结果

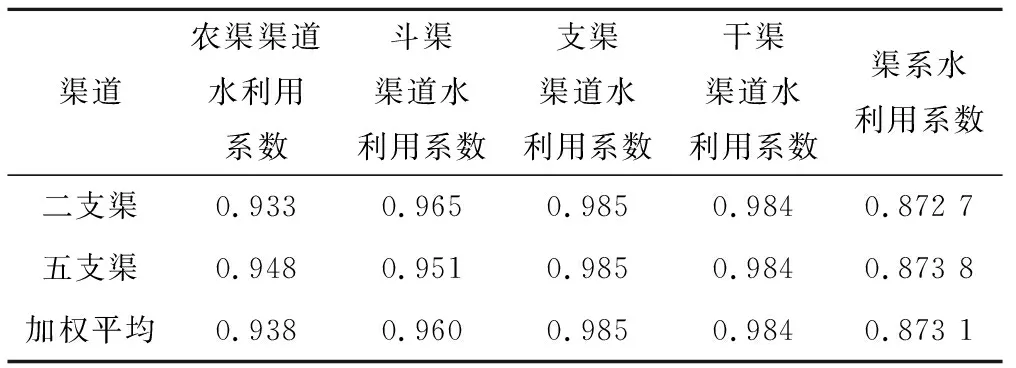
表9 改进经验公式法的渠道水利用系数计算结果

表10 由渠道净流量与毛流量比值推求的渠系水利用系数结果

3.2 小 结

改进经验公式法的计算中，由公式计算的各级渠道水利用系数连乘求得的渠系水利用系数为0.873，较由级渠道净流量与逐级推算得到的干渠渠首流量(毛流量)的比值得到的渠系水利用系数结果0.839有所不同。由于经验公式法计算过程中采用某级渠道的灌溉水利用系数作为扩大指标来计算同级其他渠道流量不能真实反映整个渠系情况，较实际情况存在偏差，因此从渠系水利用系数定义出发结果0.839更合理些。同时在用改进经验公式计算时，考虑了衬砌和地下水影响时，混凝土衬砌材料对渗漏水量的折减比例很大(根据表1，折减了约90%)。根据实地调研，灌区渠道防渗材料遭到不同程度的破坏，渠道大多存在不同程度的漏水情况，但经验公式中的相关参数未及时修正，因此改进经验公式求得的结果反映了渠道在某种衬砌状况下的渠系水利用系数。

4 结 论

(1)为解决现行渠道利用系数测算工作量大、影响因素复杂、测算精度难以控制的问题，根据渠道连续渗漏理论分别对传统计算渠道单位长度入渗损失系数的Kostiakov经验公式进行了改进，提出了改进单位长度渠道损失流量的计算公式，公式如下：

(2)以赣抚平原灌区二干渠土壤、衬砌材料等为背景，对渠道输水净流量为0.05～20.00 m3/s，渠道长度为0.05～40.00 km的测量和分析表明，改进Kostiakov经验公式与原公式相比，2者的相对误差为0.01%～46.00%，渠道的流量越小、渠道越长，Kostiakov经验公式计算结果与积分改进公式计算结果的相对误差逐渐增大。

(3)以赣抚平原灌区二干渠的实测资料为背景，改进经验公式计算得出渠系水利用系数为0.873，较由级渠道净流量与逐级推算得到的干渠渠首流量(毛流量)的比值得到的渠系水利用系数结果0.839有所不同，由于改进经验公式法计算过程中采用某级渠道的灌溉水利用系数作为扩大指标来计算同级其他渠道流量不能真实反映整个渠系情况，较实际情况存在偏差，因此从渠系水利用系数定义出发结果0.839更合理些。根据实地调研，灌区渠道防渗材料遭到不同程度的破坏，渠道大多存在不同程度的漏水情况，但经验公式中的相关参数未及时修正，因此改进经验公式求得的结果反映了渠道在某种衬砌状况下的渠系水利用系数。