不同形态海湾的水底平衡剖面研究

苏文亮，邹志利*，张庆民

( 1. 大连理工大学 海岸及近海工程国家重点实验室，辽宁 大连 116024)

1 引言

海湾地貌对自然环境变化（河流来水来沙减少、海面上升等）和人类活动的影响（滩涂围垦、跨海大桥建设等）十分敏感，认识海湾地貌的形态特征和演化规律、科学地利用海湾对自然环境保护和社会发展具有重要意义。世界上多数的海湾（或者潮流占优的河口湾）是宽度呈收缩型的，如我国的黄茅海和杭州湾都是喇叭形的河口湾，国外这样的海湾如阿曼湾、泰晤士河口等。其中，黄茅海河口湾的宽度在湾口大约为24 km，在湾顶大约为2 km，湾顶收缩为湾口的1/12。与此对应的另一类数量较少的海湾是宽度呈扩张型的海湾，如我国的湛江湾。

海湾地貌形态除了取决于海洋地质结构的塑造外还受到海湾内泥沙运动输移所导致的淤积和冲刷的影响，后者是形成海湾地形形态的主要动力因素。这一动力因素包括水动力（潮流、波浪和径流）、泥沙输移和地形演变三者耦合相互作用。目前世界上的许多海湾的水底形态已经趋近于一种平衡状态，即已经形成了海湾平衡剖面[1－2]，但人们对于这些海湾地形平衡形态的研究（特别是理论和计算模拟的研究）仍然处于发展阶段。早期的研究表明[3]，由于涨潮流和落潮流的不对称性，海湾的净输沙是沿海湾向陆地端输移的，这样如果海湾水底初始时是平底，泥沙将沿海湾淤积，在靠近陆地的海湾区域逐渐形成一个斜坡水底，最终形成向岸方向逐渐抬升的平衡剖面。Schuttelaars和de Swart[4]采用水深平均水流运动和泥沙输移的一维数学模型来分析短尺度（长度远小于潮流波长）矩形海湾地形演变，发现矩形海湾平衡剖面是一向岸方向水深均匀减小的平面斜坡。Schuttelaars和de Swart[5]于2000年又对长尺度（长度大于潮流波长）的矩形海湾进行了数值模拟，所得到的平衡剖面呈现出靠近入口处冲刷，然后沿着向岸方向呈现上凸型变化的形态，这与实际海湾地形剖面不是很符合，他们把这归因于离岸边界水深取为固定值所导致。Hibma等[6]在上述模型的基础上对边界条件进行改进，得到了与实际较为符合的海湾地形形态。这些研究都是针对宽度不变的理想情况的海湾，Lanzoni和Seminara[7]考虑宽度逐渐变小的海湾，采用了宽度积分的一维浅水方程来计算地形平衡剖面，所得结果为下凹的形态。Todeschini等[8]采用数值模拟综合分析不同海湾收缩程度、潮位幅值和水底摩擦条件下的海湾平衡剖面，发现海湾收缩程度越大、潮位幅值越大，平衡剖面的长度将越短。与以上研究都集中在宽度不变和宽度变小的海湾形态不同，Meerman等[9]考虑了宽度变大的海湾，预测其平衡剖面为上凸形。在理论解方面，Prandle[10]研究了三角形截面海湾的平衡剖面解析表达式，给出的海湾水深h与离开湾口距离x的关系为h～。除针对三角形断面这一特殊形式的海湾平衡剖面的理论解，目前还没有见到针对一般形式海湾的有关解。

本文给出了实际可能存在的收缩型、扩张型和矩形3种海湾形态的平衡剖面的理论结果和数值模拟结果。推导了海湾平衡剖面和时均悬沙浓度的解析表达式，应用水深平均水平二维计算模型数值模拟了3种海湾平衡剖面和时均悬沙浓度，二者结果进行了对比，验证了所得解析解的适用性。

2 海湾平衡剖面近似表达式

海湾形成平衡剖面的条件是：海湾泥沙输移的净输沙率在潮湾分布均匀或者在各个位置都为0。这一条件是指潮周期平均的结果，其并不意味着在一个潮周期内的任何时刻的输沙率都为0，因此，海湾平衡形态是一个相对的动态平衡。本节将通过理论分析来给出海湾平衡剖面的近似解析表达式。

2.1 理论分析

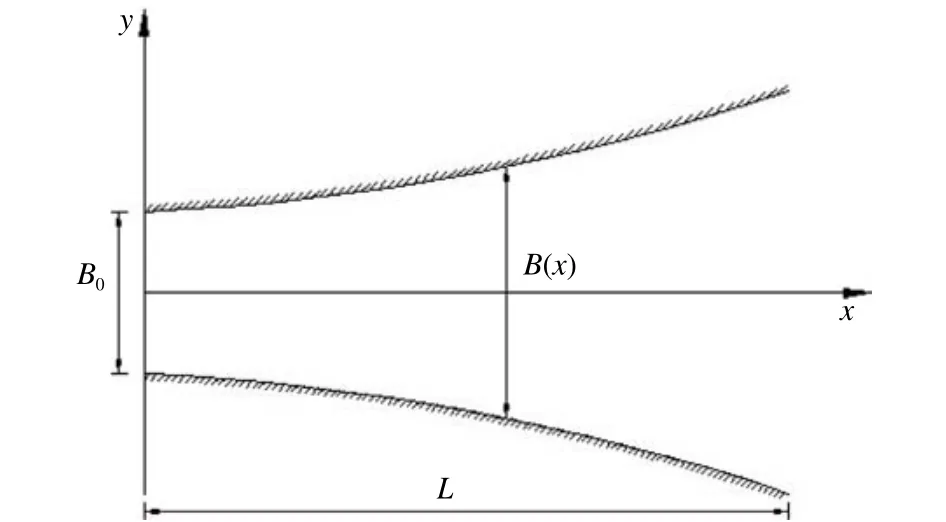
图1 坐标系（以扩张型海湾为例）Fig. 1 Coordinate system (divergent embayment)

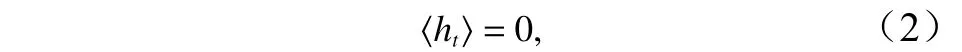
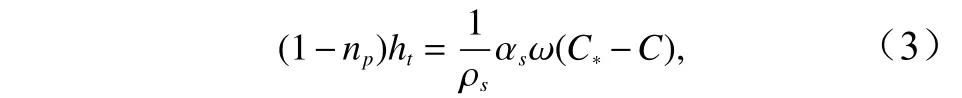
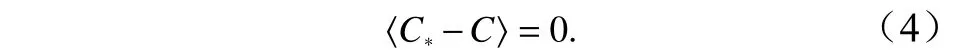
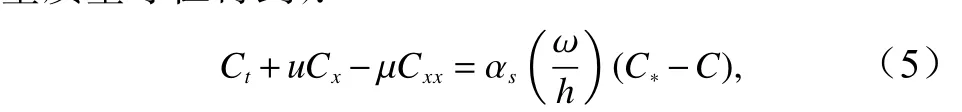
式中，μ为泥沙扩散系数。考虑海湾长度相对于潮波波长非常小的情况，这样的海湾内潮流的水面升高和速度的幅值变化很小，所以可以取u的幅值空间分布是近似均匀[4]，即

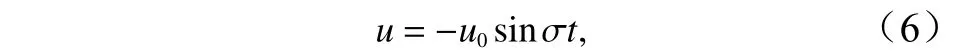
式中，u0为速度幅值；为潮流圆频率。进一步假定海湾宽度远小于长度，有＜＜1，从而有以及（可由式（20）验证）。对方程(5)取潮周期平均，在以上假定下可以在方程中忽略项和项，由于地形平衡时，时均（潮周期平均）含沙量时间变化率为0（），可得该方程时均后的首阶近似为

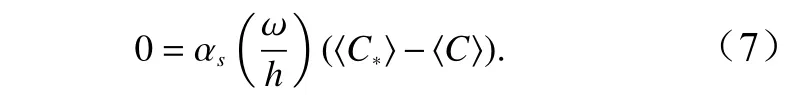
2.2 矩形海湾

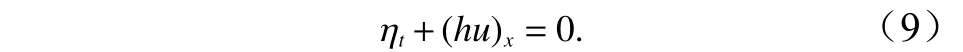
如前面所述，这里考虑的海湾为短尺度的，湾内潮位空间变化很小，于是可假设潮位沿空间分布均匀，整个海湾内水面有如下形式：

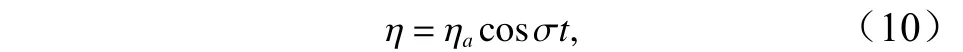
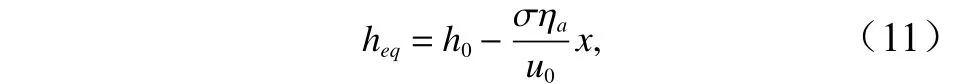
式中，h0为海湾入口处水深。上式事实上即是海湾平衡水深，因为其对应的速度u（式（6））和悬沙浓度C（式（8））满足地形平衡方程（4）。由此可知，矩形海湾平衡时剖面呈平面斜坡形状。Schuttelaars和de Swart[4]也推导出了以上矩形海湾的形如式（11）的平衡剖面表达式，但其所采用的悬沙浓度输移方程与常用的式（5）不同，方程右端沉积和落淤项采用了水深积分的悬沙浓度，而这里采用的式（5）的浓度是水深平均体积含沙量。

以上推导仅应用了连续方程，没有应用水流动量方程，这是因为对短尺度海湾，水面变化非常小，其空间梯度接近于0，动量方程可自动满足[4]。

2.3 收缩型和扩张型海湾

对收缩型和扩张型海湾，考虑水深和宽度积分的流动连续方程（线性化的）

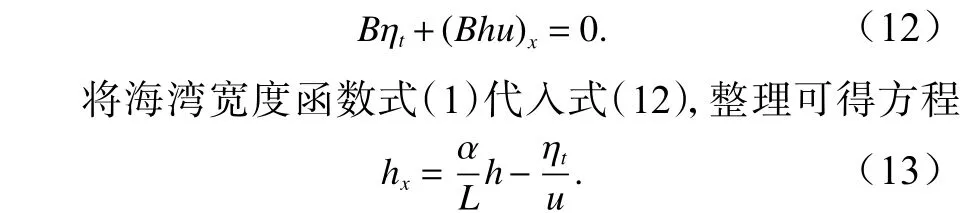
将速度u表达式（6）代入式（12），可得水深h控制方程

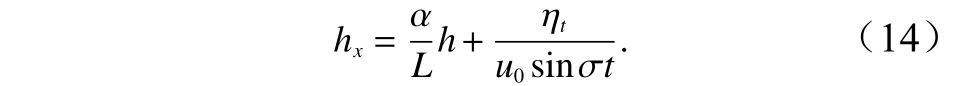
与矩形海湾均匀水面不同，收缩型或扩张型海湾由于宽度的变化可能使得水面也存在沿海湾长度方向的相应变化。因为海湾宽度变化是呈指数型的（式（1）），这里假定水面升高沿海湾方向变化（x方向）也具有指数型的，并且随时间呈现周期性的正弦变化（对应于潮流流速的表达式（6），参见式（10）），即具有以下形式的表达式：

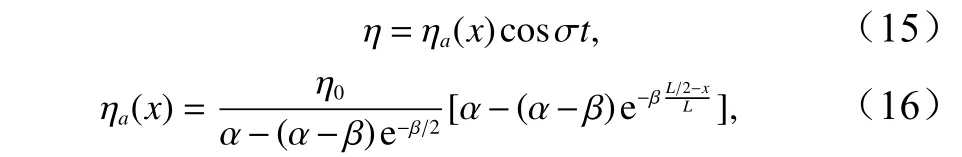
式中，η0为海湾入口处潮位的幅值；β为表达水面沿海湾变化的待定参数，这一参数的值对不同的海湾是不同的，在本研究中它们的取值将通过拟合数值解来确定。将以上水面的表达式代入方程(13)，可得水深的解为

式中，h0为海湾入口处水深。该解包括齐次解式（17）右端第一项和特解式（17）右端第二项。齐次解系数D是由海湾入口水深为h0确定的。式中潮位对平衡剖面的影响是由参数β来反映的，海湾宽度变化对平衡剖面的影响是由参数α反映的。上式给出的水深变化整体上呈现指数变化趋势，既可表达上凸地形，又可表达下凹地形，具体形式可从第3节的有关结果中看出。

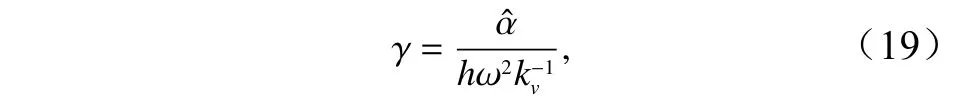
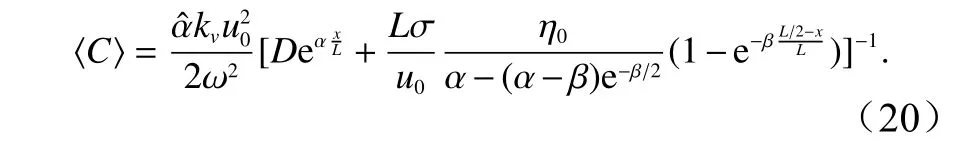
3 数值模型及验证

数值计算采用水深平均水平二维计算模型。模型包括水流连续方程、动量方程、悬沙输移方程和地形演变方程。各方程具体形式如下：

连续方程

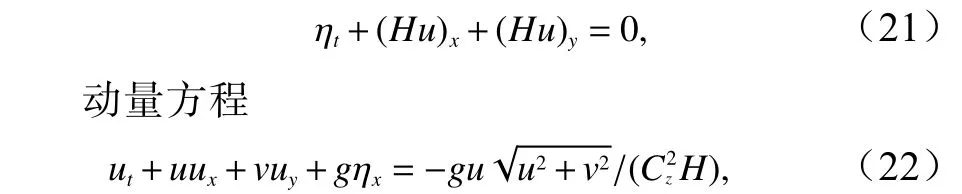
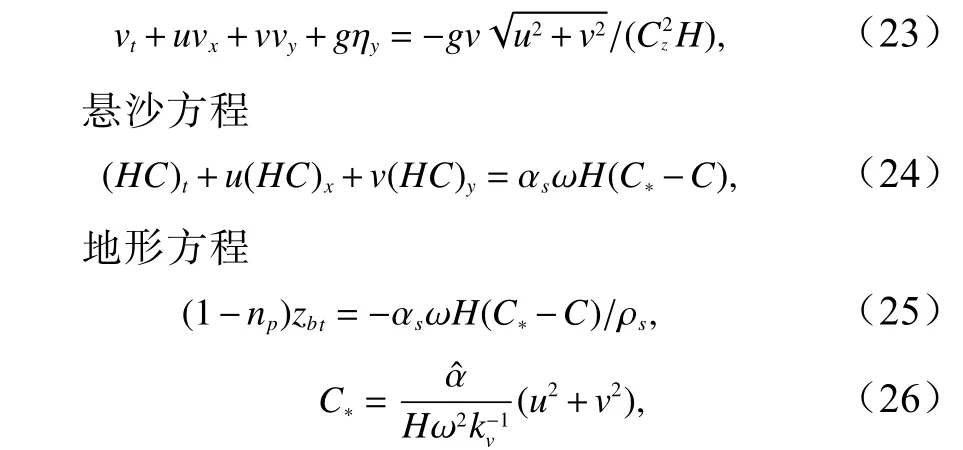
式中，H为总水深，H=h+η；g为重力加速度；Cz为谢才系数，Cz=h1/6/nr，nr为糙率，这里取 0.1；np为孔隙率，取值为0.4；zb为底床高程；为饱和悬沙浓度；，。后面两个参数的取值对应泥沙中值粒径为0.2 mm[11]。

计算的边界条件为：离岸边界为给定潮位，海岸边界为考虑水面爬坡的干湿边界，两侧边界为固壁边界。

水动力方程和泥沙输移方程采用交替方向隐式差分格式(ADI格式)求解，地形演变方程采用Liu等[12]在ENO格式基础上提出的加权基本无振荡格式(WENO格式)，该格式不仅具有ENO格式在间断区分辨率高、在光滑区计算精度高的优点，还具有截断误差阶数较高的特点，可精确模拟地形方程可能存在的间断解。

以上模型计算结果的验证是通过与Todeschini等[8]的宽度积分的水平一维模型的计算结果进行对比来实现的。Todeschini等[8]应用该模型计算了一收缩型海湾的平衡剖面，海湾长L=40 km，宽度参数的值为0.88（式（1）），入射潮波为规则半日潮，潮位幅值为2.0 m。计算中，入口处水深h0=12.5 m，初始地形为平面斜坡，坡度为h/L=1∶3 333。与Todeschini等[8]的计算一致，岸线处边界没有考虑水面爬坡，所以关闭了干湿边界条件，而是取海岸边界的静水水深为0.5 m。在达到平衡状态时，潮位幅值、速度幅值和水底剖面的对比结果如图2所示。图中结果表明，本文水平二维模型的结果与Todeschini等[8]的水平一维模型的结果符合良好。

4 数值计算结果

下面将应用以上介绍的计算模型对收缩型、扩张型和矩形3种形态的海湾的平衡剖面分别进行数值模拟，同时利用所得结果验证第2节中海湾平衡剖面和时均悬沙浓度的解析解，式（15）和式（20）。

4.1 收缩型海湾

图2 水面幅值、 速度幅值、水底剖面h计算结果和水平一维模型的结果(Todeschini等[8])的对比Fig. 2 Comparison of the calculation results of surface elevation, velocity amplitude , bottom profile with horizontal one-dimensional model (Todeschini et al.[8])

海湾平衡剖面的数值模拟一般都是以百年为单位，属于长期模拟。因此在数值计算中采用Roelvink[13]所述的加速因子。其原理是在一个潮周期计算完成后，以这个周期的地形变化的数倍代替数个周期的地形变化，以这个周期的潮位和速度代替数倍潮周期的潮位和速度。计算表明，该海湾的计算模拟在95年后可达到平衡状态，对应的水面、速度和水底剖面结果如图4所示。图中水面幅值沿空间变化很小，速度幅值沿空间变化整体上也是很小，基本与第2节中的速度假设式(6)相符合，只是在靠近岸线（x=20 km）区域出现幅值降低，这是由于此处水面升高η远小于水深h的假定已经不是很满足，存在非线性影响。图中水底剖面水深较大的前半段可以看出明显的下凹形态，后端靠近岸线区域存在地形隆起，其形成原因是由于岸线附近是潮间带，实际上存在泥沙净淤积。计算中将岸线处理为干湿边界，所以模拟出了在潮间带区域的泥沙向岸净输运产生的泥沙沉积。

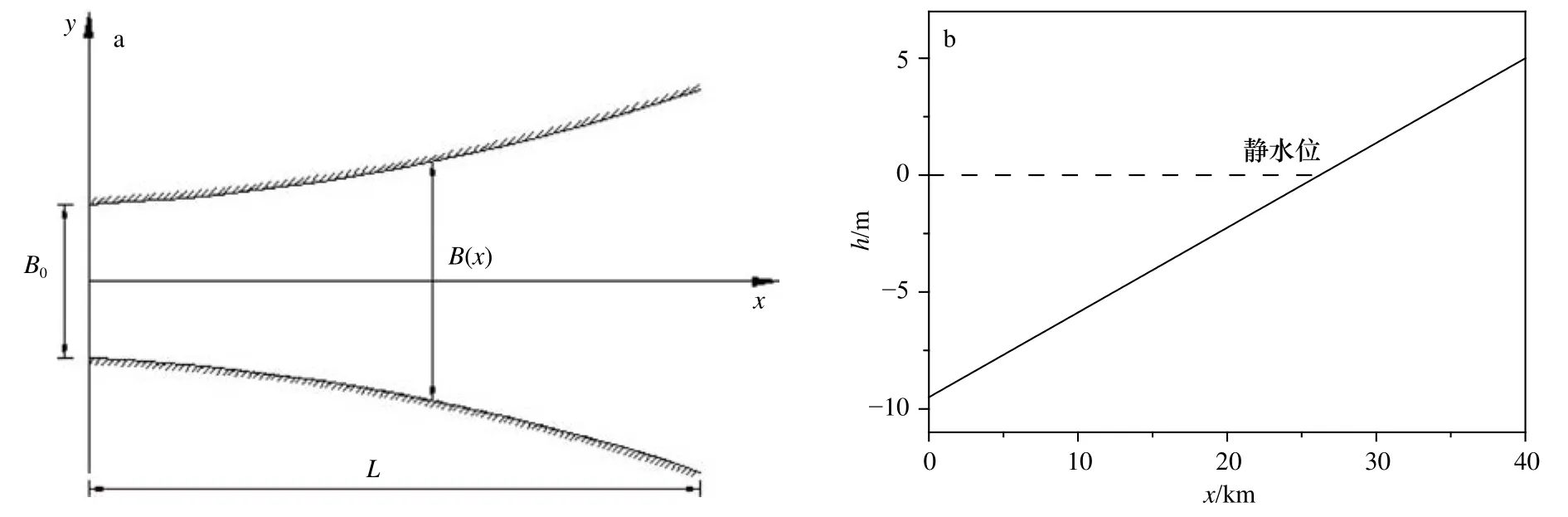
图3 收缩型海湾地形几何形态(a)和初始地形(b)Fig. 3 Geometry(a) and initial terrain (b) of convergent embayment

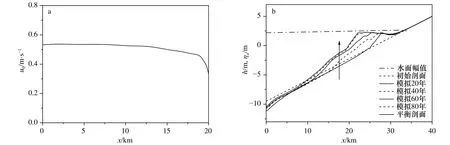
图4 收缩型海湾速度幅值(a)、水面幅值空 间分布和地形剖面h演变(b)Fig. 4 Distribution of velocity amplitude(a), surface elevation and terrain profile evolution(b) in convergent embayment

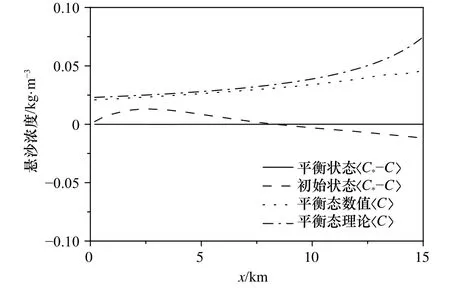
图5 收缩型海湾时均浓度差和悬沙浓度的空间分布Fig. 5 Distribution of suspended sediment concentrationand difference in convergent embayment

由图5和图6也可看出收缩型海湾水面、时均悬沙浓度和水深空间变化特征：水面幅值和时均悬沙浓度整体是略有变大，中间呈轻微下凹的形态；对应的水深h空间变化特征是呈下凹趋势的。

4.2 扩张型海湾

取扩张型海湾的长度与上面收缩型海湾的算例一样为L=40 km，入口处宽度为=5 km，宽度参数为α=-0.88。入射潮波也与收缩型海湾的算例一致：幅值为2.2 m的规则半日潮。海岸边界为考虑水面爬坡的干湿边界。初始水底剖面和上述收缩型海湾的相同，海湾平面几何形态如图1所示。

计算中发现扩张型海湾地形达到稳定需要130年的时间，比收缩型海湾的95年要长很多。达到平衡后的水面幅值、速度幅值和水底剖面如图7所示，图中也给出了在实现平衡剖面过程中不同时刻（20～100年）的水底剖面。水底地形的空间变化特征是：与收缩型海湾不同，平衡剖面整体上呈上凸形态，在海湾入口7.5 km长的区域出现冲刷，之后出现淤积。水面幅值沿空间变化很小，速度幅值在前半部分变化不大，基本符合第2节中速度具有常数幅值的假定，但岸线附近部分存在有一段向上的突起，这是由于岸线处泥沙淤积导致水体向岸爬坡所致。初始时刻和地形平衡时悬沙浓度差值在海湾内的分布如图8所示，可见，在达到平衡状态时已经变得非常小。

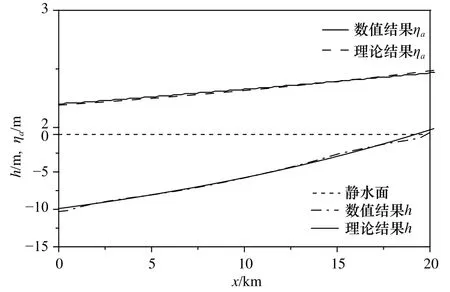
图6 收缩型海湾水面幅值、平衡剖面h数值结果和解析解结果对比Fig. 6 Comparison between numerical result and analytical result of surface elevation and equilibrium profile in convergent embayment

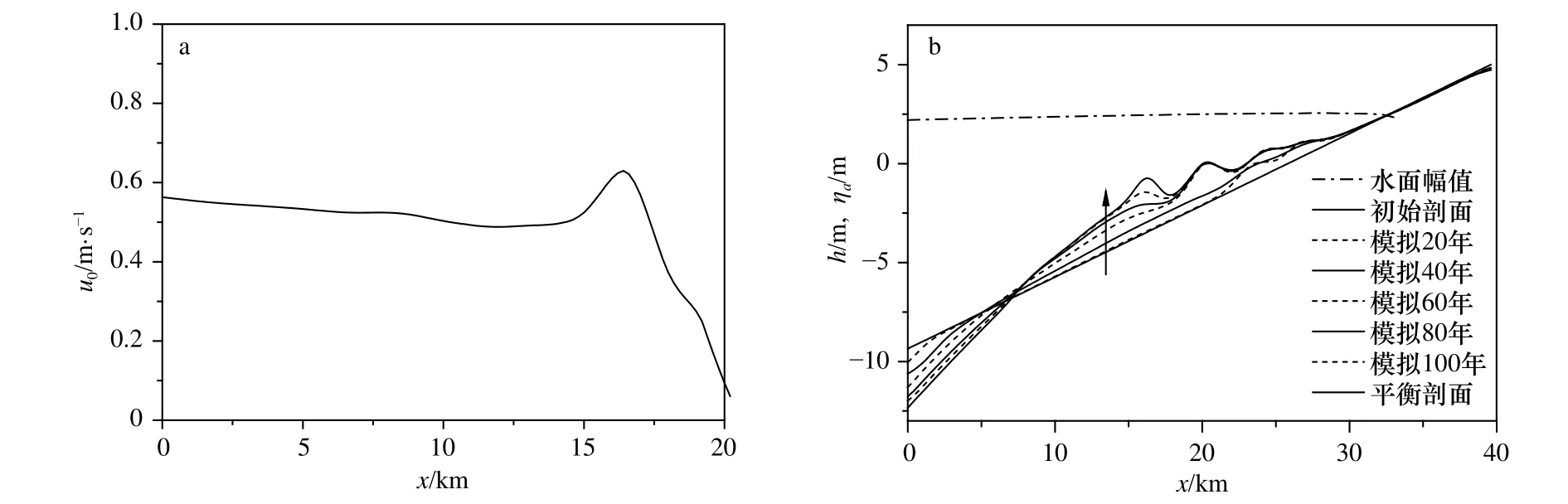
图7 扩张型海湾速度幅值 (a)、水面幅值空间分布和地形剖面h演变(b)Fig. 7 Distribution of velocity amplitude (a), surface elevation and terrain profile evolution (b) in divergent embayment

将水面解析解（16）与图中水面的前半段进行拟合（图9），可得参数取值为β=-0.7。将该参数值代入式（14）和式（20）可计算出理论结果的平衡剖面和时均悬沙浓度，分别如图9和图8所示。通过与图中数值结果对比可以看出，二者相互吻合，只是水深结果在靠近岸线（h=0）的浅水区域存在一些差别，这是由于不能满足建立解析解所采用的水面升高远小于水深h的线性假定所致。

下面对图7a中x=16 km附近区域出现的速度突起给出进一步的说明。事实上，当取水底地形为理论解（17）时，该突起将消失。为了说明这一点，将计算水域中20 km区域水深固定取为理论水底，然后重新计算速度结果。图10给出了相应的速度值，图中也给出了数值计算水深及其对应的速度曲线。可见，对应于理论水深的速度在海岸附近呈现渐进缓慢变化、没有出现突起，而对应于数值计算水深的速度是存在这一突起的，这表明，后者的速度突起是由水底隆起所引起的。

图8 扩张型海湾时均浓度差和悬沙浓度的空间分布Fig. 8 Distribution of suspended sediment concentrationand difference in divergent embayment

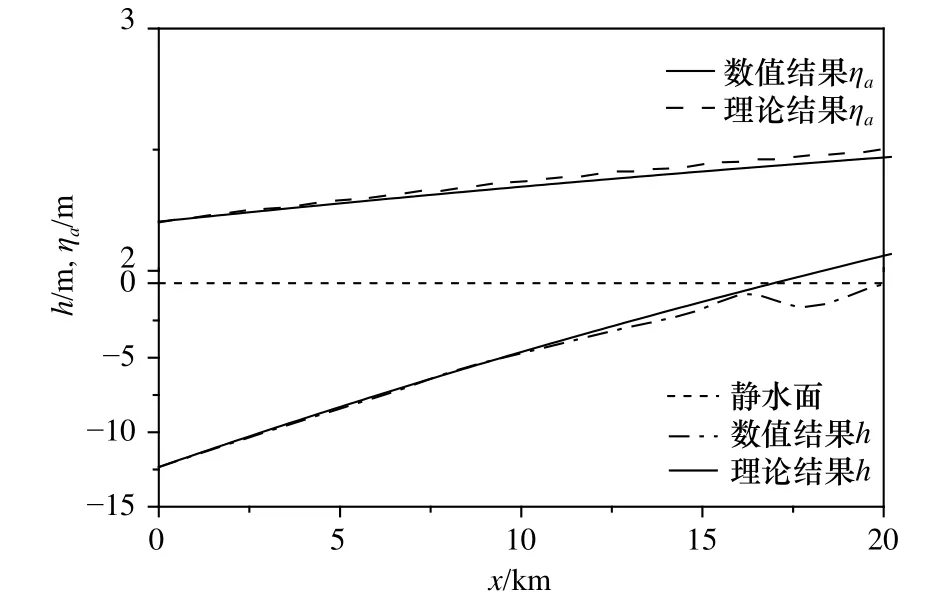
图9 扩张型海湾水面幅值、平衡剖面h数值结果和解析解结果对比Fig. 9 Comparison between numerical result and analytical result of surface elevation and equilibrium profile in divergent embayment

图10 取水底地形为理论解(15)时速度幅值分布及其与数值计算的速度分布的对比Fig. 10 Distribution of velocity amplitude correspond to analytical solution(15)

4.3 矩形海湾

取矩形海湾长度为L=40 km，宽度为B=2 km，入射潮波和收缩型、扩张型海湾的相同。初始地形同样采用平面斜坡。相比于收缩型海湾和扩张型海湾，矩形海湾明显更快的达到平衡剖面，在模拟90年时剖面就已经不再变化，结果如图11所示。图中水底平衡时明显的表现为平面斜坡形态，这和理论结果式（11）一致。图中潮位幅值和速度幅值变化很小，与第2节的常数幅值假设相符合，图12给出了有关对比结果以及水底剖面h理论与数值结果的对比。悬沙浓度差如图13所示，平衡时浓度差也是非常小的。该图中也给出了平衡地形所对应的时均悬沙浓度的理论结果（式（20）中）与数值模拟结果的对比，二者符合很好。

5 讨论

本文的分析采用了短尺度海湾的假定，这使分析过程大为简化，该假定的突出特点是潮流速度沿海湾长度的变化可以忽略，其仅随时间做周期性变化，该流场所导致的潮周期平均海湾水底剖面自动成为平衡剖面，因为随时间正弦变化的潮流速度可以满足海湾内潮周期平均含沙量不随时间变化的条件（式（8））。由上节解析解结果与数值解结果对比可见，基于以上简化所得到的u和η以及平衡水深h和含沙量的理论结果仍然是可以和数值计算结果相符合的。下面对其中的原理，即对建立这些解析解所涉及的有关近似处理的合理性做进一步说明。

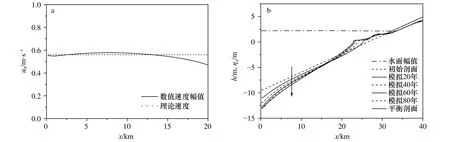
图11 矩形海湾速度幅值分布(a)、水面幅值和地形剖面h演变(b)Fig. 11 Distribution of velocity amplitude (a), surface elevation and terrain profile evolution (b) in rectangular embayment

图12 矩形海湾水面幅值、平衡剖面h数值结果和解析解结果Fig. 12 Numerical result and analytical result of surface elevation and equilibrium profile

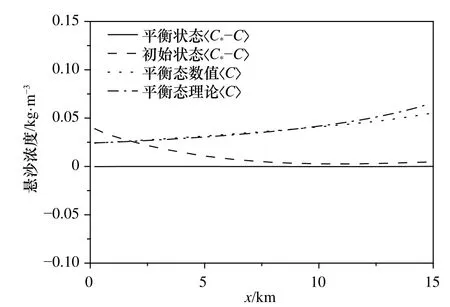
图13 矩形海湾时均悬沙浓度和时间浓度差的空间分布Fig. 13 Distribution of suspended sediment concentrationand difference in rectangular embayment

（1）关于海湾潮波水位和速度表达式的选择。本研究对潮波速度采用了式（6）表达形式，且取其幅值为常数，对潮位采用了式（15）和式（16）的表达形式，为了说明这两个表达式的合理性，除考虑连续方程（12）之外还需要考虑海湾内潮波的动量方程。在连续方程中忽略非线性项（乘积项），在动量方程也同样地忽略非线性项，并忽略海湾横向速度v, 因为其相对纵向速度u很小（），则可得线性化的水深平均连续方程和动量方程为（考虑海湾宽度变化并不改变动量方程的形式，参见Todeschini等[8]）

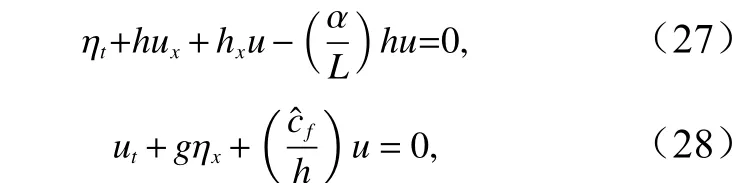
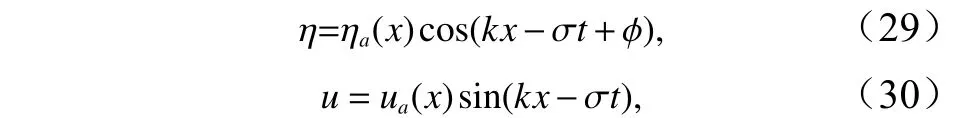
式中，φ是水底摩擦导致的水位与速度之间的相位差（摩擦相位角）；和是幅值。k在这里并不是潮波的波数，而是一个与相位差 φ一样的待定量，事实上，这两个量都是(是潮流波数)阶小量，在最后的水位和速度的表达式中是可以忽略掉的，但在方程求解过程中是需要的，这可从下面推导中了解到。将以上两式代入方程（27）和（28）可求得方程解，见附录中式（A8）、（A9）和（A10）。图 14 给出了收缩型海湾幅值原来的表达式（16）与新的表达式（A8）的变化曲线以及在取不同水底摩擦系数时的变化曲线。由图中结果可见，原来的表达式与新的表达式的结果具有相同的变化趋势，但原来的表达式更与数值模拟结果接近。的结果中时的结果更与数值模拟结果接近。

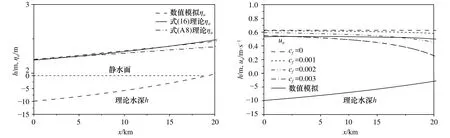
图14 水面幅值和速度幅值的理论解（收缩型海湾）Fig. 14 Theoretical solution of surface elevation and velocity amplitude (convergent embayment)

（2）关于水面η解析表达式中参数。由以上理论推导可以看出，当速度u的表达式已知时，仍然需要水面η和水深h二者之一是已知的才可确定另外一个量（h已知可确定η，或者η已知可确定h）。这表明，在线性理论的范围内，表达水动力和地形演变耦合的方程系统还不是封闭的（可证，即使考虑三维流动结果也是这样），只有考虑非线性系统式（21）至式（26）才可以使系统自行封闭，这是因为线性解一般只能给出水底地形的增长趋势，但不能给出该增长达到平衡时的状态，后者属于有限幅值效应，需要对地形演变进行非线性分析才能得到。在这种情况下，需要引入一个参数（即以上解中的参数）来使系统封闭。该参数是取决于海底平衡剖面的长度大小，所以事实上它也是海底平衡剖面所包含的参数，只不过本研究将其转化为水面表达式中的参数。因为海湾潮位比水底地形更容易观测和确定，所以这样的转化是把水底地形形态这样一个不容易确定的问题转化为水面变化这样一个容易确定的问题。

（3）关于线性理论的限制。上面的理论推导和第2节的理论分析都忽略了η和u自身乘积和相互乘积的有关项，即忽略了非线性项，这导致所得结果不能考虑非线性效应。波浪非线性的大小在短波（深水波）情况是由波高与波长之比（波陡）来表征的，在长波（浅水波）情况是由波高与水深之比来表征的[14]。潮波属于浅水波，所以其非线性的大小是由比值来衡量的，即在的幅值远小于水深h的情况下，线性理论才适用。这使得本研究所得理论解不适合h较小的靠近岸线附近区域。数值模拟结果表明，这一区域存在水面爬坡形成的泥沙淤积，导致了存在突出的地形隆起，这会影响速度幅值空间分布和时均悬沙浓度的空间分布。

6 结论

本文采用了短尺度海湾（海湾长度远小于潮汐波长）假定研究了海湾平衡剖面的确定问题，由于海岸潮汐波长尺度一般在500 km量级（半日潮），所以本文研究结果适合于长度为十几或者几十千米的海湾。基于该假定，理论分析和数值模拟研究结果给出了收缩型、扩张型和矩形3种典型海湾平面形态所对应的海湾平衡剖面，得到了这3种类型海湾平衡剖面的解析解及其对应的时均悬沙浓度的解析解，并与水深平均二维数值模型的计算结果进行对比。研究所得结论如下：

（1）对于长度远小于潮流波长的短海湾，海湾内潮流速度幅值可以假定为常数。这一假定为本文数值计算结果和线性理论分析结果所证实：矩形海湾平衡地形的流场速度幅值沿空间是均匀分布的，收缩型和扩张型海湾的速度幅值在海湾的水深较大区域也基本是均匀分布的，但在靠近海岸的浅水区域会受到局部水底淤积隆起和较大的水底摩擦的影响，呈现偏离均匀分布的变化。

（2）基于海湾内潮流速度为常数的假定建立了短海湾平衡剖面的解析解和对应的时均悬沙浓度解析解。解析解对应的收缩型和扩张型海湾的水面升高沿海湾存在微小空间变化，这与等宽的矩形海湾的均匀水面有所不同。所建立的海湾水面解析表达式含有一个待定参数β，表征海湾宽度变化的影响（β的值与宽度参数的值符号相同，二者对收缩型海湾大于0，对扩张型海湾小于0，对矩形海湾等于0），所以，在实际应用中，可根据具体海湾的水面观测结果来确定。本文利用数值模拟结果确定了这一参数的值，基于这一水面表达式而得到的海湾平衡剖面的解析解及其对应的时均悬沙浓度的解析解与数值结果符合很好。

（3）所得到的平衡剖面对收缩型海湾呈下凹形态，对扩张型海湾呈上凸形态，平面形态居于二者之间的矩形海湾的平衡剖面呈平面斜坡形态。

（4）平衡剖面对应的时均悬沙浓度沿海湾分布整体呈现缓慢升高趋势，在靠近海岸区域升高变快。

以上研究结果不适合海湾长度接近或大于潮汐波长的长尺度海湾情况，如何对这类海湾的平衡剖面进行解析分析是今后研究的一个值得关注的课题，目前该方面的研究还仅有数值方面的结果（Todeschini等[8]）。

附录：

1 海湾水位和速度的求解

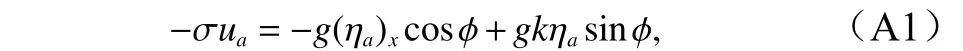
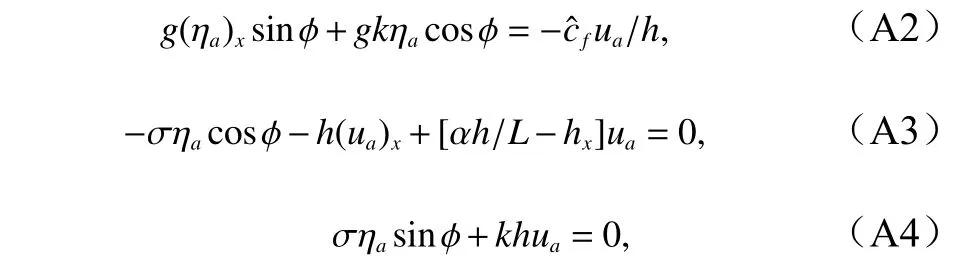
把式（A8）代入方程（A6）可得速度幅值表达式

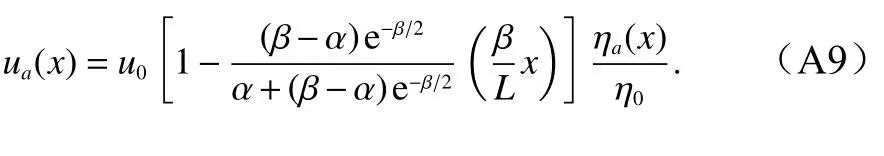
式（A8）和式（A9）中

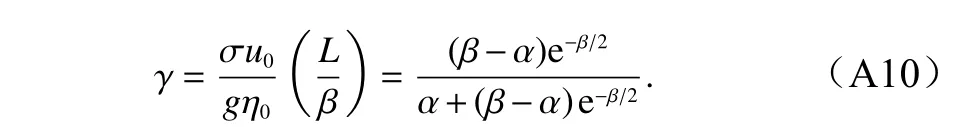
进一步可由方程（A2）和（A4）求得波数k和相位角 φ，为了避免复杂的推导过程，这里采用近似处理，即直接采用水深为常数时的结果，后者可以容易在方程（A1）至(A4)中取水深为常数而得到，结果为

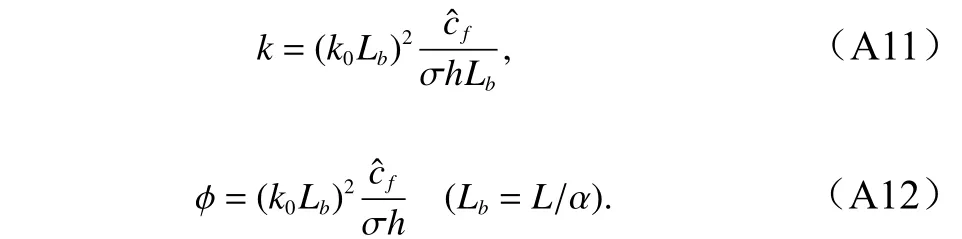
为了考虑实际水深是变化的，可将以上表达式中水深h取为当地水深（变水深）。