关于Boussinesq型水波方程理论和应用研究的综述

孙家文，房克照，刘忠波，范浩煦，孙昭晨，王平

( 1. 国家海洋环境监测中心 国家环境保护海洋生态环境整治修复重点实验室，辽宁 大连 116023；2. 大连海事大学 交通运输工程学院，辽宁 大连 116026；3. 大连理工大学 海岸和近海工程国家重点实验室/DUT-UWA海洋工程联合研究中心，辽宁 大连 116024)

1 引言

波浪从深水传播到浅水的过程，存在反射、折射与绕射、浅化以及近岸水域破碎等复杂的物理现象。在这一过程中，波-波非线性相互作用、波浪的频散以及潮流等背景水流的存在，让水波呈现出更加复杂的形态。海港码头、防波堤等水工建筑物，防止海滩侵蚀等突堤工程和潜堤工程以及各类人工岛工程等的建设，都应充分考虑波浪荷载。设计波浪对于海岸工程建设有十分重要的意义，精确把握从一定深水到工程前沿范围内的波浪情况十分必要。近年来，伴随着计算机性能的突飞猛进，波浪数值模拟成为极为有效的方式，这又进一步促进了各类水波理论模型，如缓坡类水波方程、Boussinesq型水波方程和非静压水波模型等的发展。下面主要从理论推导和数值应用两个方面对1967-2018年间常用的Boussinesq型水波方程研究历程进行回顾。

1872年，法国科学家Boussinesq[1]假定水深为常数，垂向速度沿水深呈线性分布，得到一组水平一维弱色散的非线性方程，开启了对Boussinesq类水波方程研究的大门，后人为纪念他的重大贡献称该方程为Boussinesq方程。其后国内外学者也推导了很多此类水波方程，称为Boussinesq型（类）水波方程。

Peregrine[2]于1967年推导了可以考虑水深变化的水平二维Boussinesq型水波方程，该方程后来被称为经典Boussinesq型方程，其水平一维表达形式为

经典的Boussinesq型方程有如下特点：（1）控制方程为质量守恒的连续方程和无黏不可压动量方程，其中动量方程中的时空三阶混合导数项称为色散项，是Boussinesq型方程区别于浅水长波方程的主要标志。（2）以波面和水深积分平均速度为变量，该方程可以模拟波浪折射、绕射、反射和波浪间的相互作用等；其中，波浪绕射体现在二阶色散项中存在对空间x和y的混合导数；波浪非线性相互作用主要源于和项。（3）该方程是弱色散性和弱非线性的，其中非线性参数和色散性参数分别是（ A为波幅，h为特征水深）和（L为特征水深），弱非线性与弱色散性假定是指，这表明方程的色散适用范围是有限的，仅适用于浅水区域的波浪模拟，当波浪相速度误差不大于5%时，其适用水深仅约为0.2倍深水波长，满足不了实际工程对水深的要求；而弱非线性则表现为方程中与二阶色散性相匹配的非线性项的缺失。（4）该方程不能考虑环境水流的影响，因为方程中没有包含水流引起的波长变化的多普勒效应项，如与相关的项。（5）尽管国内外学者习惯称呼方程（1）为精确的连续方程，但其中的速度和方程（2）中的速度是同一变量，由于方程性能限制，该速度并不精确。因此，方程（1）仅在表达形式上是精确的，其他以水深积分平均速度表达的Boussinesq型方程均存在同样问题。（6）方程中不含有垂向速度，这将复杂的三维水波问题简化为二维水波问题，因而大大提高了计算效率。

克服上述经典Boussinesq方程存在的缺陷和不足需要引入评价模型精度的度量标准。在建立方程的色散关系式与Stokes线性波色散关系式的关联问题上，Witting[3]的工作是开创性的，其成功引入了Padé逼近的方法，为Boussinesq型方程色散参数的确定提供了一种最直接有效的方法。为了改善经典Boussinesq型方程在色散性、非线性、波流相互作用等方面的性能，国内外众多学者做出了不懈的努力，极大推动了Boussinesq型方程的发展。本文以方程中是否含有明显的垂向速度为标准，将Boussinesq型水波方程分为水平二维和三维两种情况。多数Boussinesq型水波方程归纳为水平二维方程，控制方程中不存在明显的垂向速度，其在推导过程中表达为水平速度的显式函数。这将最终方程的空间维度减少了一个，因此三维复杂问题简化成水平二维问题是众多Boussinesq型方程的一个最显著的特征，其带来的最大便利就是数值模型的计算效率得到了相当程度的提高。而另外一类则是三维Boussinesq型方程，它的显著特征是垂向速度在控制方程中仍是独立未知量。伴随着计算机硬件技术的发展和并行计算技术方法的出现，三维Boussinesq型方程的计算效率已不再是一个主要限制。事实上，Boussinesq型方程是势流理论，三维Boussinesq型方程在精度方面不断逼近以Laplace方程为控制方程的势流理论，并且计算效率比三维波浪势流理论要高。因此，三维Boussinesq型水波方程顺应了当前海岸（海洋）工程的发展需求，也是水波理论研究领域的前沿方向之一。

2 Boussinesq型水波方程的理论研究

2.1 水平二维Boussinesq型水波方程

2.1.1 注重改进色散性能

Madsen等[4-5]在动量方程中人为加入含有待定系数的三阶项，通过与精确线性色散关系的Padé展开拟合确定系数，使方程的色散性达到了O(μ2)（在允许色散性误差为5%时，kh≤3，k为特征波数）。Madsen等[4]方程系数的确定也考虑了Witting的工作，进而Madsen和Sørensen[5]首次给出了Boussinesq型水波方程的变浅作用系数，该方程后来发展为MIKE软件中的BW模块，已被广泛地用于海岸和近海工程中波浪数值模拟。该方程以通量形式表达，含有不完整的二阶非线性项。由于方程推导时通过采用长波方程假定引入了三阶项，水平速度沿垂向分布的表达式将不再适用，类似的问题也存在于以水深积分平均速度表达的其他Boussinesq型水波方程中。

与Madsen等理论推导工作不同，Nwogu[6]从欧拉方程出发，建立了以波面位移和沿水深任意处速度为基本变量的弱非线性Boussinesq方程，通过确定速度具体位置Zα可使方程色散性精确到Airy波精确解的Padé[2, 2]阶近似。Nwogu推导的方程仅包含弱非线性项，其形式上完全类似于经典Boussinesq型水波方程的弱非线性项。推导该方程的初始目的只是为了改善方程的色散精度。有趣的是，该方程的水平速度沿垂向分布是二阶表达的，精度却相对较高，明显优于Madsen等[4-5]的方程。在应用Nwogu[6]方程进行数值模型时应注意，在取水平速度位置为Zα=-0.531h时，方程的浅化作用性能较差。

Schäffer和 Madsen[7]对 Nwogu[6]模型进行了色散适用水深的扩展，得到了一个含有5个待定参数的改进型Boussinesq方程，通过优化待定参数的取值，可使色散性精确到Airy波精确解的Padé[4, 4]阶近似，使其应用水深达到kh≤6。Chen和Liu[8]给出了以水平速度势和波面位移表达的改进型Boussinesq型水波方程，进而又将方程进行了频域化处理。与Madsen等[4-5]采用的长波假定类似，Beji和Nadaoka[9]在经典Boussinesq方程基础上，引入一个改善色散性的参数，推导出一组改进色散性的弱非线性Boussinesq型水波方程。林建国等[10]在经典Boussinesq型水波方程基础上，首先引入变换速度取代水深积分平均速度，继而采用类似Schäffer和Madsen[7]的方式，最终给出了一组以变换速度表达的弱非线性Boussinesq型水波方程，该方程的色散适用水深也达到kh≤6。与以上处理方式不同，张永刚和李玉成[11]在Nwogu[6]模型基础上，采用了两个不同位置处的速度，并以两层速度进行加权的方式重新改写连续方程，给出了一组新型的弱非线性Boussinesq型水波方程，该方程的最大色散适用水深也是kh≤6。

以上这些方程主要为了改善经典Boussinesq型水波方程的色散精度，方程中的二阶非线性项或被忽略，或部分保留，导致方程仅具有弱非线性特征。同时，大多数方程变量对空间的导数最高为3，其中有的方程是引入了项，有的是原始方程本身就含有类似项（速度u可以是某一水深处的速度，也可以是伪速度（计算速度））。为了避免求解三阶空间导数，Zhao等[12]推导了一组以波面位移和水平速度势表达的弱非线性二阶Boussinesq型水波方程，该方程最高空间导数仅为2，便于数值计算程序的开发。

2.1.2 注重改进线性变浅性能

Madsen和Sørensen[5]首次给出了Boussinesq型方程变浅梯度的概念。其后，Chen和Liu[8]和Schäffer和Madsen[7]也强调了变浅作用。Beji和Nadaoka[9]认为，对他们的方程而言，无论采用Madsen等[4-5]推荐的方式，还是从能量守恒角度出发，两种方式推导的变浅梯度是一致的，这引发了Schäffer[13]的讨论。事实上，采用能量守恒或Madsen等推荐的方式恰好适用Beji和Nadaoka的方程，一些变浅系数的引入则有助于改善方程的变浅性，我们更认同Schäffer的观点。另有 Zou[14-15]，Lynett和 Liu[16]，Liu 和 Sun[17]也对针对变浅作用的改善进行了研究。近年来一些学者，如Galan等[18]和Simarro等[19]在Chen和Liu[8]提出的线性变浅波幅基础上，对前人的一些Boussinesq型水波方程进行色散和变浅性能改善时系数选择上进行了一定的探讨和研究，认为通过适当选择系数可较大幅度提高变浅作用性能。与Simarro等[19]的观点类似，刘忠波等[20]则又强调，采用计算速度（伪速度）取代原方程中的速度变量可以改善如Lynett和Liu[16]和Wei等[21]的Boussinesq型方程在色散性和变浅性能方面的性能。

2.1.3 注重改善非线性性能

不同频率波浪之间相互作用时，除产生与各自频率成整倍数的高阶非线性波幅外，还会产生和频（频率相加）与差频（频率相减）波幅。通常用Stokes波的二阶、三阶波幅以及和（差）频波幅来考察Boussinesq型方程的非线性性能。

Wei等[21]将Nwogu[6]的Boussinesq型方程发展到近似到二阶完全非线性，美国特拉华大学Kirby团队以该方程为基础开发了FUNWAVE模型，由于代码开源，在国内外得到了广泛的应用，诸多学者利用该数值软件进行了更为广泛的科学研究工作，在较大程度上提升了该方程的知名度。必须注意，该方程的变浅性能与Nwogu[6]的Boussinesq型方程一样，是具有短板的，后续Kirby团队采用了双层加权形成伪速度模式改进了该方程的变浅性能。但遗憾的是，这一改进未能体现在后续开发的各版本FUNWAVE代码中，因而这一问题也引发了Simarro[22]对该方程的系数选取方面的讨论。但Choi等[23]在回复中的观点表明，针对均化统计变量而言，两组不同系数的计算结果类似。尽管Simarro的讨论是合理的，但在理论方面的做法上存在一定的问题，其以牺牲色散精度换取了变浅性能的改善，而原方程的色散精度较高，变浅性能差一些，加上计算的范围特定，客观上很难比较出二者的优劣。为了避免这一情况，在不牺牲色散精度前提下，刘忠波等[20]引用伪速度（计算速度）的做法更应值得关注，而这一做法的源头起源于Zou[15]。

Madsen和Schäffer[24]在对前人Boussinesq理论相关文献分析与评述基础上，从Laplace方程出发，结合自由面的动力学和运动学边界条件以及水底的运动学边界条件，系统地推导了以水深积分平均速度或某一处水深速度表达的具有四阶非线性特征的Boussinesq型水波方程，并详细研究了方程的色散性、变浅性、二阶和三阶非线性波幅、波幅离散引起的频散效应、二阶和差频特征和波流相互作用问题。该文献是Boussinesq型方程理论研究的经典文献。Chondros和 Memos[25]将 Madsen 和 Schäffer[24]的一组以水深积分平均速度表达的Boussinesq型方程中的定常参数改为与无因次水深相关的变化参数，并在理论分析中强调了该方程在线性色散关系与二阶非线性性能（同Stokes波浪理论相应解析解比较）是精确的，这引发了Liu和Fang[26]的关注和讨论。对于线性规则波来说，将参数与无因次水深关联可能是有效的，但考虑到近岸水波多以不规则波为主，即便非线性规则波在地形上演化也会产生高频或低频波。因此这种做法无法同时精确描述多个不同频波浪的色散性，类似地，也不能确保方程具备良好的和差频特性。因此，他们的做法是无效的，并且不具备普适性。

邹志利[27-29]给出了具有近似到二阶完全非线性的Boussinesq型方程，其中文献[27]是从Laplace方程出发，从水底关于垂向z对速度势做展开，并综合考虑了方程的高阶与低阶非线性相互作用和引入改善变浅性能的系数，得到了以波面位移和水深积分平均速度表达的Boussinesq型方程。在此基础上，采用了伪速度（计算速度）取代水深积分平均速度，又可延展为新的高阶Boussinesq型水波方程[28]。文献[29]则是从欧拉方程出发，引入了垂向坐标变换，继而给出了适合复杂地形的近似到二阶完全非线性的Boussinesq型方程，最后从理论方面讨论了方程在复杂地形上的波浪Bragg反射和透射特性。

Gobbi等[30]发展了Wei等[21]的Boussinesq型水波方程，将方程的非线性由二阶提高至四阶，其引入了伪速度势的概念，即采用两层不同位置处的水平速度势加权形成新速度势，推导出一组具有Padé[4, 4]色散关系的Boussinesq型方程。该方程最大的优势在于水平和垂向速度沿着水深分布的精度均超过了同时期所有Boussinesq型方程。然而该方程的变浅性能至今仍没有被优化，加上该方程含最高空间导数为5阶的项，数值离散较为困难，导致该方程并没有得到广泛应用。此外，Zou和Fang[31]从欧拉方程出发，引入垂向坐标变换，推导出一组四阶全非线性Boussinesq水波方程，方程中最高导数也是五阶，同样存在数值离散和实际应用困难的情况。

Lynett和Liu[16,32]从欧拉方程出发，经过严格的数学推导，得到了具有近似到二阶完全非线性的两层和多层Boussinesq型方程。他们将一层二阶完全非线性Boussinesq型方程拓展到多层，实际上是为了获取更高的色散精度并且也避免求解空间导数超过三阶（不含3）情况下的数值解，这开启了多层Boussinesq型方程的研究模式。从理论分析结果来看，多层方程的水平速度沿垂向分布特征更为精确，非线性性能也得到了一定程度的改善，但适用范围仍远小于色散性能。该方程对应的计算模型已经开发成公开源代码的COULWAVE软件。类似于Lynett和Liu的工作，Liu和Fang[33]则从Laplace方程出发，推导出3组具有不同色散精度的双层Boussinesq型方程，特别是第3组的色散性能得到了较大的拓展。

林建国和邱大洪[34]、Hong[35]及Liu和Sun[17]分别推导了不同精度的非线性Boussinesq型水波方程。在方程非线性特性改善研究方面，Kennedy等[36]选取与波面位移关联的水深速度变量，这一定程度上改善了Wei等[21]方程的二阶非线性（含和频）性能，但却很难实质性改善差频性能。以水深积分平均速度表达的Boussinesq型方程的改进工作可参见刘忠波等[37]和Fang等[38]研究，同样，这些研究工作仅改进了规则波对应的高阶波幅和波-波相互作用的和频性能。

2.2 三维Boussinesq型水波方程

水平二维Boussinesq型方程的发展集中于改善色散、变浅以及部分非线性性能，而非线性适用水深远远小于色散性适用水深，速度沿水深分布的精度较差，这是水平二维方程最致命的缺陷。在水平二维Boussinesq型方程中，垂向速度通过水底方程并利用水平速度显示表达，在大幅度提高计算效率的同时，也不可避免地降低了非线性性能。综合考虑应用水深和其他各种性能精度，上节所述的水平二维Boussinesq型方程的使用范围受到限制，不能满足当前深海工程对强非线性波浪、波浪与结构物相互作用的计算需求，发展具有更高精度、具有三维特征的Boussinesq型水波方程成为趋势。为了提高非线性性能，垂向速度保留在方程中是有必要的。Agnon等[39]给出了一组高阶的三维Boussinesq型水波方程，该方程在色散精度、变浅精度、二阶非线性精度等方面的适用水深均达到了kh=6，其改善非线性的做法主要是分离了方程非线性与色散性。该三维方程保留了水底边界条件、自由面上波浪的动力学方程和运动学方程以及采用静止水位的水平速度和垂向速度表达的全域速度场。其最大的缺点是速度沿水深分布的精度较低，最大适用水深为kh=2.0。其后，Madsen等[40-41]首先用水深某一处的速度取代静止水位的速度，进而采用计算速度（伪速度）来取代水深某一处速度，得到了一组具有综合性能优良的三维Boussinesq型方程。在色散性方面，该方程最大适用水深为kh=25～40，非线性性能在这一量级具有较高精度。其中垂向分布的速度可适用于kh=12。方程中最高空间导数为5，当最高导数退化为3时，色散适用水深kh=10，速度分布精确到kh=3.5左右。

Chazel等[42]结合Madsen等[40]及Lynett和Liu[16]的做法，给出了最高空间导数为2、以伪水平速度势（计算速度势）和伪垂向速度表达的双层三维Boussinesq型方程。方程的色散适用水深约为kh=20，速度垂向分布的精度最大达到kh=6～8，但是他们并没有分析波浪的二阶和三阶非线性特征以及不规则波之间的和（差）频特征等。刘忠波等[43]结合Madsen等[40]及Lynett和Liu[16]的做法，给出了平底情况下空间导数为3和5的双层高阶Boussinesq型方程，继而考虑了缓变地形变化的水深条件。Liu和Fang[44]进一步给出了空间导数为3、以伪水平速度和垂向速度（计算速度）表达的双层三维Boussinesq型方程，方程的色散适用水深约为kh=53，速度垂向分布的精度可以最大达到kh=23.2，同时二阶非线性特征和不规则波的和（差）频特性大为改善。在这一工作的基础上，Liu等[45]一方面将这个方程推至多层，并详细分析了三层与四层方程的性能。理论分析表明，方程得到了空前的发展，其中四层方程的色散适用水深达到kh=667～800，非线性性能达到了kh=300，速度分布精确到kh=352～423，线性变浅在0＜kh≤300内具有较高的精度；另一方面，他们也给出了具有最高空间导数为2和5的多层Boussinesq型方程。最高导数为5时，四层模型的色散适用水深达到了kh=7 600；导数为2时，四层模型的色散适用水深为kh=179.3，图1给出了四层方程的色散关系。

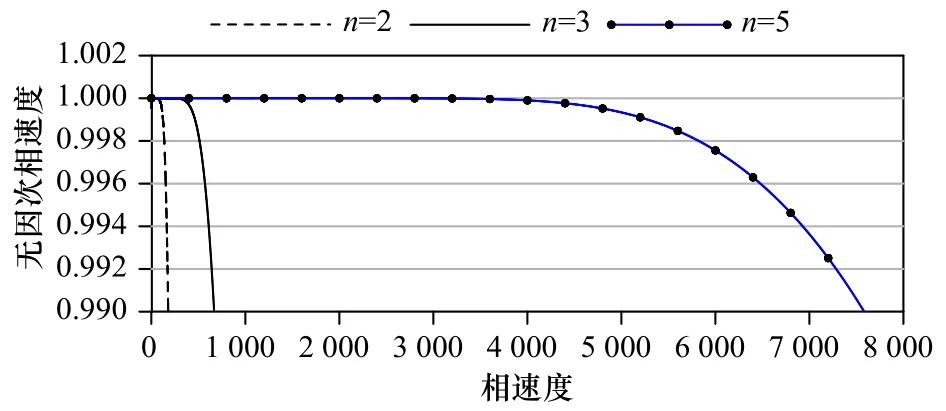
图1 四层Boussinesq方程的相速度（n代表方程中的最高导数）Fig. 1 The dimensionless phase celerity of the four-layer Boussinesq equations (n is the highest order of the spatial derivative)

综合多年研究，将具有代表性的Boussinesq型方程汇总在表1中，并给出了这些方程在色散性、二阶非线性和线性变浅性能、速度分布特征等方面的适用水深。

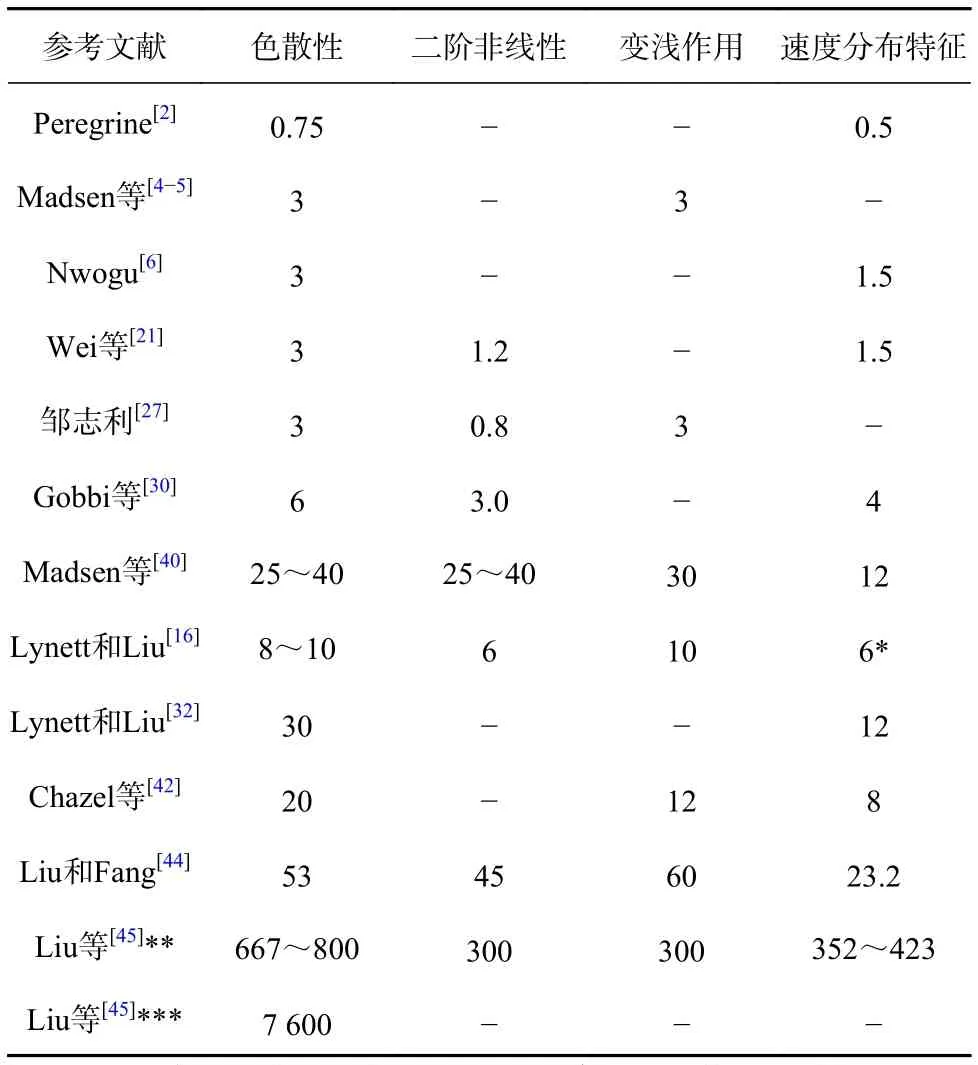
表1 Boussinesq型水波方程的最大适用水深（kh）Table 1 Maximum application water depth of different Boussinesq-type models

2.3 适合特殊情况的Boussinesq型水波方程

2.3.1 考虑地形渗透

Cruz等[46]假定渗透介质中的水体也近似满足Laplace方程，考虑了渗透介质对水体的非线性阻力和线性阻力，结合上部自由水体的Laplace方程，推导了一组适合渗透地形的改进型Boussinesq型方程。在不考虑渗透情况下，该方程可以转化为一组仅改善色散性的弱非线性Boussinesq型方程。Hsiao等[47]和Chen[48]从欧拉方程出发，分别推导了以某一处水深速度表达的高阶Boussinesq型方程，两文献中的基本方程推导思路是相似的，但是后者更强调了波流相互作用、有旋引起的非线性高阶项的处理和四阶渗透阻力项的引入。刘忠波和孙昭晨[49]对Hsiao等[47]的一组以水深积分平均速度表达的Boussinesq型方程进行了色散适用范围的拓展，其后刘忠波等[50-51]又直接耦合了两组不同高阶的Boussinesq型方程和Cruz等[46]渗透介质中水体的动量方程，最终给出了一组混合Boussinesq型方程。在充分考虑前人研究基础上，刘忠波等[52]从Laplace方程出发，考虑了渗透介质对水体的阻力效应，推导出3组近似到二阶完全非线性的Boussinesq型方程。这些模型考虑了一层渗透水体和一层自由水体情况。在单层渗透和多层渗透介质中波浪传播方程研究中，Hsiao等[53]推导了一组以渗透介质某一处速度表达的Boussinesq型方程，刘忠波等[54]则推导了3组考虑双层渗透介质情况下的Boussinesq型水波方程。

无论是从Laplace方程还是从欧拉方程出发，均能推导出适用渗透介质情况的Boussinesq型方程。这类方程在色散性和衰减率等性能方面取得了一定的进展。目前，由于难以从理论层面给出不同渗透情况下的理论变浅解析，使得如何优化变浅性能成为一个遗留的问题。另外，在衰减率性能方面的改进仍有较大空间。

2.3.2 考虑水体密度分层

与相对成熟的自由表面波Boussinesq型方程相比，采用Boussinesq型方程考虑界面波（内波）的研究还相对较少，但多数方程与自由表面波的研究方程有一定的联系。在推导方程中，其中一个假定是密度分层（密度不连续），继而从Laplace方程或欧拉方程出发，考虑刚盖假定或自由面存在波动等情况，推导出不同形式的Boussinesq型方程。如Choi和Camassa[55-56]、Lynett和 Liu[57]、Song[58]、Liu 等[59]、Yang 等[60]以及Liu和Wang[61]等。其中Song的方程可以退化为Nwogu的Boussinesq型方程，Yang等的内波方程退化为Madsen和Schäffer以水深积分平均速度表达的四阶方程。

受实验室条件的限制，采用有限水深假设研究内波的实验还十分稀少，这很大程度上限制了Boussinesq型内波计算模型的发展。在大尺度范围，内波主要表现为内孤立波等形式，采用弱非线性Boussinesq型内波数值模拟内孤立波的研究相对较多。在当前海洋工程日益挺进深远海、海洋工程装备需求不断增大的背景下，采用Boussinesq型方程来研究内波尚存巨大的发展空间。

3 Boussinesq型水波方程的应用研究

数值模型的建立是联系Boussinesq水波理论和实际应用的桥梁。数值模型通常建立在有限元、有限差分、有限体积以及有限差分-有限体积混合模式基础上，Brocchini[62]和Kirby[63]关于Boussinesq型水波方程在数值模型计算方法等方面进行了较好的综述，这里我们不再展开评述，下面仅从工程与科研角度，对Boussinesq型方程在自由表面波的模拟应用方面加以简述。

3.1 工程中波浪的时域演化

Boussinesq型水波方程的一个主要用途是通过模拟确定对工程荷载产生影响的设计波浪。数值模型需要指定入射边界条件和出口边界条件，而入射边界条件往往需要借助于外海推算或采用浅水波浪谱模型给出。一般来说，这类模型适用的计算区域属于中等尺度，特别是近年来GPU并行技术的发展以及高性能计算机的出现，促使这类水波方程的数值计算区域更大，如近期Tavakkol和Lynett[64]在Madsen和Sørensen[5]的Boussinesq型水波方程基础上，基于并行技术，发展了一套CELERIS软件，该软件计算效率大为改善。据作者称，计算速度比实际波浪演化快。模拟中，必须清楚认识到现实中的波浪资料等推算方面存在不确定性，加上其他一些因素，实际工程中的波浪模拟并不能如科学研究那样可以精准关注某些位置点的波面位移时间历程，这主要体现在波面相位的精准性难有精确的现场衡量标准。此外，二阶Boussinesq型方程很难适用于深水情况，在深水条件下，我们建议可选择Lynett和Liu[16]的双层水波模型（COULWAVE模型）为主要模拟工具。此外，刘忠波等[20]对该方程的色散性能和变浅性能进行了改进，发展了以计算速度表达的双层水波模型可作为数值模拟的有力工具和补充。

3.2 工程中波生流的应用研究

Boussinesq型方程大多是基于势流理论建立起来的，因而其在本质上不能考虑波浪破碎。为了能近似地考虑波浪破碎带来的能量消耗，通常采用人工紊动黏性法、水滚法和涡度法。这使得Boussinesq型模型可以计算波高、波浪增减水、波浪爬高以及波生沿岸流和裂流等[65-68]。从以往计算结果与实验结果的对比来看，统计量下的精准度是可以接受的。波生流会驱动污染物运动和泥沙运动等物质输运，较小的流速误差对污染物运动和海底泥沙输运的精准预报产生较大的影响，这无疑对波生流的准确性提出更高要求。此外，也应该注意Boussinesq型方程是否正确地考虑了水流的多普勒效应[69]。从人与自然亲近和谐的角度考虑，如一些海滨浴场所处的近岸海域，波浪破碎引起的离岸流（裂流）会对泳者带来生命安全隐患。采用Boussinesq型数值模型或引入波浪辐射应力的浅水模型对波生流进行高效预报或应重点考虑。

3.3 海床运动兴波的研究

海床运动引起的兴波可分为两类，第一类是由地震引起的海啸波，第二类是海底滑坡运动引起的海啸波。准确预报海啸波抵达时间以及在近岸幅度大小均要求计算模型具有较高精度的色散性和非线性特征。近年来，一些学者应用不同精度的Boussinesq水波模型来模拟海床运动导致的海啸波产生、传播演化和近岸爬高[70-73]。在这些研究中，海床运动多假定为刚体，其运动导致兴波是通过海底运动学边界条件实现的，导致海啸波产生过程过于简化。精确再现海床运动以及传播演化中的波浪幅度，都要求模型具有较高的精度，在使用时需要注意Boussinesq型方程的适用范围。也有学者将Boussinesq类方程用于库区山体滑坡诱发波浪的传播模拟，由于方程具有色散性，在模拟兴波传播过程中较不含色散性的非线性浅水方程更为准确，但研究中多将滑坡体视为刚体，而实际中山体滑坡多为松散体。海床运动兴波在近岸的爬高和淹没范围是工程界关注的焦点，计算中涉及水陆交界面，动边界的有效处理也是不容忽视的。

3.4 工程中其他波浪问题的应用研究

为了有效控制波浪对岸滩的侵蚀，工程师通常会建设一座或多座潜堤来消耗波浪，这类工程在海岸水域较为常见。抛石潜堤一方面反射波浪，另一方面由于潜堤中渗透孔隙与水体之间存在线性与非线性阻力，导致波能产生损耗，从而有效减少透射波浪。利用波浪Bragg反射共振原理，合理布置多座潜堤将增加波浪反射率。Boussinesq方程中含水深的一阶和高阶导数项，它们在模拟波浪与潜堤相互作用时往往产生重要影响，合理优化相关参数有助于改善不同地形上的波浪反射与透射性能[74]。实践中，工程问题多关注强浪向和常浪向，特殊情况下也会考虑其他方向来浪。方案比选中，一些防护结构的平面布置往往需要考虑波浪条件，这可通过合理的Boussinesq模型计算得到。在研究以上问题时，必须明确：（1）完全适合各种陡坡地形的Boussinesq型方程并不存在，相关计算结果仍需结合现场实际情况进行核定；（2）当采用Bragg反射共振特性，一部分波浪能量反射回到来浪方向，这将与其他波浪叠加，或会对附近船舶的通航造成一定的威胁，此时，断面可选用抛石潜堤，而适合渗透的Boussinesq型方程恰好适用。

Boussinesq型模型应用范围很广，它还可用于研究河口波浪与水流相互作用、外海传入的低频波引起港湾共振、船体运动产生的表面波与内波、波浪引起的泥沙运动、近岸海床演变以及作用于建筑物的波浪力等方面的计算。

4 结语

针对1967-2018年间的主要Boussinesq方程进行了回顾，分析了常用水波方程的优缺点。作为一类高效的计算模型，其在以下几个方面尚存发展空间：

（1）在理论层面，Boussinesq型方程在一些特殊领域可得到进一步发展和完善，如前文所述的一些方程在某些性能方面存在改进空间。因此，我们关注点应进一步结合实践需求，对适应各种特殊情况的水波方程做相关研究，但始终应牢记，此类方程是波浪势流理论，研究中应明晰适用范畴。

（2）在应用层面，强调掌握水波方程基本理论特性基础上，利用已有Boussinesq方程研究更大水深的自由表面波和内波等水波水动力问题。同时，也应注重发展适合深海情况的水波模型应用，这对深水情况下Boussinesq模型的计算效率也提出了较大挑战。此外，在波浪与结构物相互作用层面，强调Boussinesq模型与其他模型的耦合势在必行。早在2002年，Qi和Wang[75]将改进的Boussinesq型水波方程和基于VOF的Navier-Stokes模型进行耦合，远场采用Boussinesq方程，近场采用Navier-Stokes模型，这充分考虑了两种模型的优点。鉴于该耦合模型中，采用的Boussinesq方程性能相对还不够精确，三维Boussinesq方程可期望成为一个更强有力的计算工具。

Boussinesq型方程在海岸波浪水动力的应用研究之路依然很长。一方面，仍要继续加强基础工作的理论研究，另一方面，更应强调理论要服务于工程实践的理念。一切理论从工程实践中来，它们也必将到工程实践中去加以检验。