高雷诺数下不同湍流润滑模型对水润滑橡胶轴承润滑特性的影响

杜媛英 李明 任兴星

摘 要：為研究高雷诺数运行工况下的水润滑橡胶轴承的润滑特性，采用4种不同的湍流润滑数学模型，利用有限差分法，首先分析了4种不同湍流模型下的雷诺数，水膜厚度，衬层变形及水膜压力分布规律;然后对不同湍流润滑模型下的雷诺数随偏心率的变化规律进行了研究;最后讨论了4种湍流润滑模型下的承载力和最大膜压随偏心率、转速和间隙比的变化。结果表明：4种湍流润滑模型下的衬层变形和最大膜压均大于层流润滑，其大小顺序为：青木弘-原田正躬模型>Ng-Pan湍流模型>Constantinescu湍流模型>Hirs湍流模型;不同润滑模型下偏心率对雷诺数的影响不大。采用湍流润滑模型计算的承载力和膜压远大于层流润滑，层流假设不再适用高雷诺数下水润滑橡胶轴承的实际运行工况，同时在此工况下采用青木弘-原田正躬湍流润滑模型比其他3种润滑模型更为合理。随着偏心率的增大，承载力和最大膜压非线性增大;随着转速的增大，承载力和膜压近似线性增大;随着间隙比的增大，承载力非线性减小，膜压近似线性增大。

关键词：水润滑橡胶轴承;湍流模型;高雷诺数;转速;承载力

中图分类号：TB 43

文献标志码：A

文章编号：1672-9315（2020）02-0321-09

DOI：10.13800/j.cnki.xakjdxxb.2020.0218开放科学（资源服务）标识码（OSID）：

Effect of different turbulent lubrication models on the lubrication

characteristics

of water-lubricated rubber bearings in high Reynolds number

DU Yuan-ying1，LI Ming2，REN Xing-xing3

（1.Engineering Training Center，Xian University of Science and Technology，Xian 710054，China;

2.College ofSciences，Xian University of Science and Technology，Xian 710054，China;

3.Department of Architectural Engineering，Pingliang Vocational and Technical College，Pingliang 744000，China）

Abstract：To study the lubrication characteristics of water-lubricated rubber bearings in high Reynolds number operating conditions，four different turbulent lubrication mathematical models were used，the distribution of Reynolds number，water film thickness，lining deformation and film pressure under four different turbulent lubrication models were analyzed using

the finite difference method.Then the variation of Reynolds number with eccentricity under different turbulent lubrication models was investigated.Finally，the variation of the bearing capacity and maximum film pressurewith eccentricity，rotating speed and clearance ratio under four turbulent lubrication models were discussed.The results show that the lining deformation and maximum film pressure of the four turbulent lubrication models are greater than that of laminar lubrication with their ordersas follows：Aoki-harada turbulence model>Ng-Pan model>Constantinescu model>Hirs model;and the type of the lubrication model has slight effect on the Reynolds number.The bearing capacity and film pressure calculated by the turbulent lubrication model are far greater than

those by

the laminar flow model，and the laminar flow assumption is no longer applicable to the actual operating conditions of the water-lubricated rubber bearings in high Reynolds number.And the aoki-harada turbulent lubrication theory is more reasonable than the other three lubrication models.With the increase of eccentricity，the bearing capacity and the maximum film pressure increase nonlinearly;with the increase of the rotational speed，the bearing capacity and pressure increase linearly;with the increase of the clearance ratio，the bearing capacity

increase nonlinearly，and the pressure increases approximately linearly.

Key words：water-lubricated rubber bearings;turbulence model;high Reynolds number;rotational speed;bearing capacity

0 引 言

水具有来源广、安全性高、环境友好等优点，是最具有发展潜力的润滑介质。水润滑橡胶轴承是滑动轴承的一种，它的内部通过膜压硫化精密成形，是特种橡胶合金材料。水润滑橡胶轴承作为水下最适宜的轴承之一，已经广泛地运用在船舶、水下航行器、水泵和水轮机等行业。由于水的粘度较低，水润滑橡胶轴承在低速，重载，过载及轴颈弯曲等特殊运行工况时，水膜厚度变化较大，润滑水膜内的实际主流流态是湍流。

到目前为止，层流润滑理论的发展已经相当成熟，但在自然科学和工程技术中，碰到最多的是湍流，研究的较为成熟的层流却较少遇到。早在1923年，

Taylor G I就对2个同心圆柱间的粘性流动进行了研究，并提出了同心圆柱间的临界雷诺数计算公式[1-2]，Taylor C M总结了湍流机理和湍流润滑理论，并将湍流理论在轴承润滑及设计中的应用做了更为深入的研究[3]。同时期，也有许多学者对湍流润滑理论做了大量研究，其中有较大影响力的如下所述：

Constantinescu V N基于混合长理论，探讨了紊流状态下的轴承润滑特性[4-5]，Ng C W，et al.基于壁面定律法提出了一种线性化的湍流理论，并分析了轴承内的湍流润滑特性[6-8]，Hirs G G按照整体流动法探讨了湍流条件下的润滑特性[9]。青木弘-原田正躬[10]理论是一种求涡扩散系数为特征的计算方法，其理论基础是壁面定律或紊流能量方程。Meinkai H和Vohr J H依据紊流能量法分析了轴承内的紊流润滑特性[11]。张直明等提出了一种紊流润滑理论分析的新方法──复合型紊流模式理论[12-13]。近年来，Cabrera D L和Woolley N H.et al.对水润滑橡胶轴颈轴承中的薄膜压力分布进行了实验研究，发现水润滑橡胶轴承与传统刚性轴承的薄膜压力曲线非常不同[14]。

Frêne J和Arghir M探讨了湍流流态下，考虑惯性力影响下的轴承内和密封件之间流体薄膜的润滑特性[15]。Shenoy B S和Pai R分析了在层流和湍流流态下外部可调节的轴承润滑特性[16]。

ShyuS H和Jeng Y R et al探讨了无限宽滑动轴承在热湍流润滑条件下的承载力[17]。王迎佳等分析了层流紊流共存时径向滑动轴承热流体的润滑性能[18]。

目前，Mallya R et al分析了紊流流态下转子不对中时复杂沟槽的静态润滑特性[19]。

Das S和Guha S K分析了极微流体动力润滑下湍流对轴颈轴承非线性稳定性的影响[20]。

Litwin W利用实验和CFD方法讨论了水润滑轴承推进轴系关键材料参数的性能对润滑特性的影响[21-22]。Gao G et al对水润滑条件下滑动轴承的润滑性能进行了数值分析[23]。Lv F et al对转子不对中情况下的混合润滑特性进行了分析[24]。

Ouyang W等讨论了接触工况下水润滑橡胶轴承的动态特性[25]。刘佳蕾利用CFD流固耦合方法探讨了水润滑橡胶轴承的热弹流润滑特性[26]。

综上，目前国内外采用数值解法对水润滑橡胶轴承润滑理论的研究和计算大都引入了层流假设，以使得问题得到简化，同时轴承中多以平均膜厚计算平均雷诺数，但水润滑橡胶轴承在实际运行时，由于橡胶的变形较大，同时水膜厚度又很薄，实际水膜内多为湍流状态，实际雷诺数也是随膜厚h的变化而变化的，以某一平均值进行计算会导致较大的误差。因此，采用湍流润滑模型，并在计算中考虑雷诺数随膜厚的变化有极为重要的实际意义。

1 水润滑橡胶轴承的结构及基本参数

1.1 水润滑橡胶轴承的结构

水润滑橡胶轴承的结构如图1所示。其中轴承中心为O;转子绕轴颈中心Om转动;ns为转速;e为偏心距;φ为偏位角;h为水膜间隙;轴承半径为R0;轴颈半径为R.转子旋转时，流体动压润滑在橡胶轴承间隙中形成。

1.2 水润滑橡胶轴承的基本参数

计算中所涉及的轴承参数见表1.

2 控制方程

2.1 雷诺方程

由于湍流方程组的不封闭性，在湍流研究发展过程中，形成了各种各样的湍流润滑模式理论。在工程实际应用中最为广泛使用的有4种湍流润滑模型，它们是Constantinescu模型、Ng-Pan模型、Hirs整体流动模型及青木弘-原田正躬模型。这4种湍流润滑模型的润滑方程在形式上均类似于雷诺方程

式中 θ为轴承在圆柱坐标下周向坐标;λ为无量纲轴向坐标;H为无量纲水膜厚度;P为无量纲水膜力;L为轴承长度，mm;d为轴颈直径，mm;kx和kz均为湍流系数。

无量纲所用特征量

式中 u為轴颈速度，m/s;c为半径间隙，mm;η为水的黏度，Pa·s.

4种润滑理论的湍流因子可以表示为表2.

2.2 雷诺数的计算

雷诺数的计算公式

Re=ρRu/u（3）

由于轴径转速随膜厚变化，因此雷诺数也随膜厚发生变化。

临界雷诺数的确定依据泰勒[1]求得的径向轴承临界雷诺数的计算公式

Rec=41.1R/c（4）

由表1的参数，求得临界转速Rec为750.

2.3 水膜厚度方程

2.3.1弹性变形模型

水润滑橡胶轴承衬层的弹性变形为[28]

式中 Δh为衬层变形，mm;p（ζ）为水膜压力，Pa;

x-ζ为压力作用点与弹性变形计算点之间的距离，mm.

2.3.2 水膜厚度方程

橡胶轴承的水膜厚度包括轴承与转子间的间隙和橡胶材料的变形。以轴承间隙c为特征长度进行无量纲化，可得到全圆周式水润滑轴承的无量纲水膜厚度为

式中 H为橡胶轴承的无量纲水膜厚度;ΔH为无量纲化橡胶弹性变形。

2.3.3 平衡方程

水膜力与载荷达到平衡时，水膜力在x轴和y轴上的分力为Wx和Wy，水膜承载力为W

3 数值计算方法及有效性

3.1 有限差分法

采用有限差分法求解式（1）。图2为求解域网格图，其中沿轴向和周向将λ和θ划分为n和m个等距区间。在求解过程中，求解域的定义为-1≤λ≤1，0≤θ≤2π.计算网格的控制域为120×120个等距的节点。

采用中心差分格式，则式（1）可表示为

APi+1，j+BPi-1，j+CPi，j+1+DPi，j-1-EPi，j=Fi，j

（8）

各项系数分别为

A=（1/kx）H3i+0.5，j

B=（1/kx）H3i-0.5，j

C=（1/kz）（dΔθ/LΔλ）2H3i，j+0.5

D=（1/kz）（dΔθ/LΔλ）2H3i，j-0.5

E=A+B+C+D

F=Δθ（Hi+0.5，j-Hi-0.5，j）

（9）

边界条件为自然破裂，由式（8）可得各节点的Pi，j.

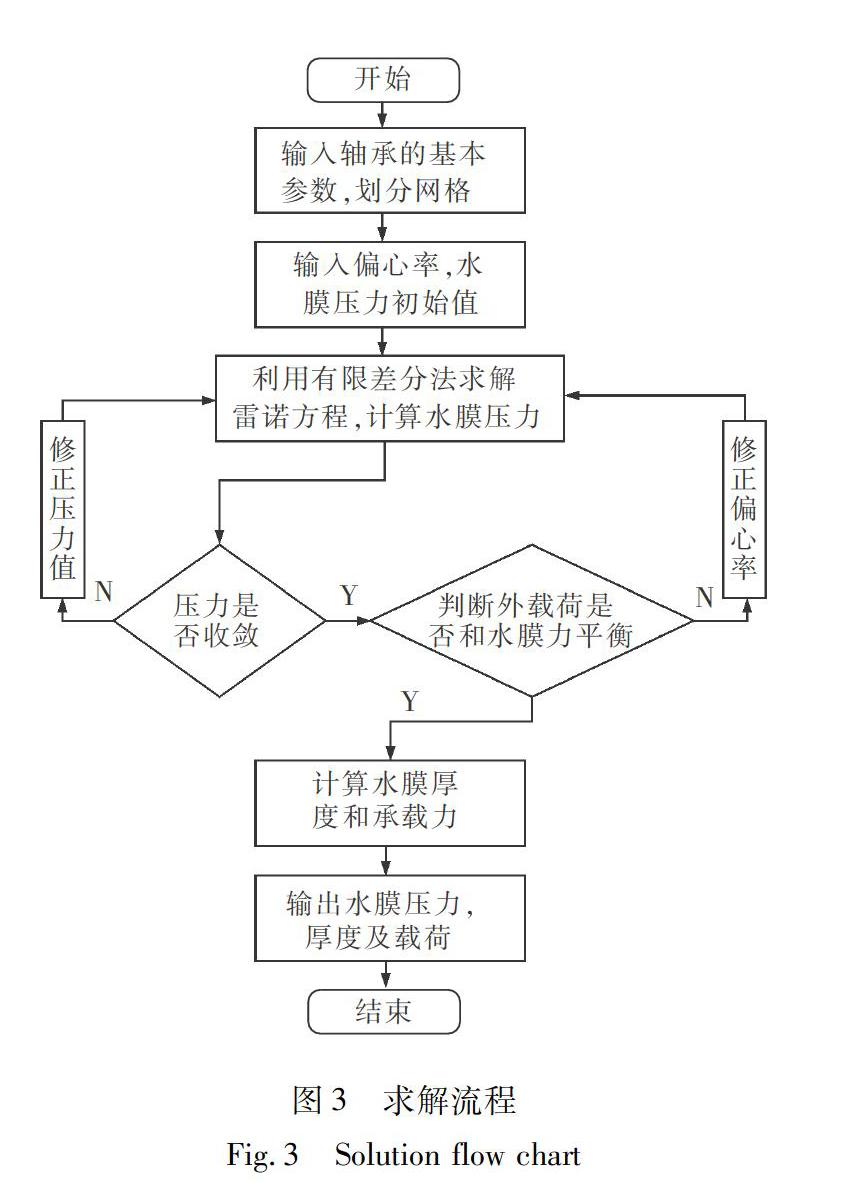
通过MATLAB编写相关分析程序，利用超松弛迭代方法提高计算的精度和效率，收敛精度均为0.001.其流程如图3所示。

3.2 数值方法的有效性

在进行数值分析前，需进行程序的有效性验证。在相同的几何和工况参数下，将本程序中青木弘-原田正躬润滑模型的计算结果与文献[23]进行比较分析。图4所示为偏心率为0.6，轴颈直径为80 mm，间隙比为0.001时，采用青木弘-原田正躬湍流润滑模型和文献[23]计算的承载力随转速的变化规律。

从图4可以看出，青木弘-原田正躬湍流润滑模型计算的承载力与文献[23]计算的结果相差在5%之内，证明本程序能有效地进行轴承润滑性能分析。

4 结果分析及讨论

4.1 不同湍流润滑模型下的雷诺数，水膜厚度，衬层变形及水膜压力分布

图5为水润滑橡胶轴承转速为600 r/min，偏心率为0.6时，采用不同润滑模型计算得到的中截面的雷诺数，水膜厚度，衬层变形及水膜压力随周向角度的变化规律。

从图5（a）可以看出，层流润滑下的雷诺数为一固定常数，4种湍流润滑模型下的雷诺数沿圓周方向的变化趋势一致，且4种模型下雷诺数的差别较为微小，可以认为润滑模型对雷诺数的影响不大。从图5（b）可以看出，在承压区，4种润滑模型下的无量纲膜厚沿周向分布趋势基本一致均呈正弦波状分布;采用湍流润滑理论计算的衬层变形均明显大于层流润滑理论，其中青木弘-原田正躬湍流模型计算的衬层变形最大，Ng-Pan湍流模型和Constantinescu湍流模型计算的变形相差不大，Hirs湍流模型计算的衬层变形最小。从图5（c）可以看出，

4种湍流润滑模型下计算的膜压沿周向分布趋势基本一致，均远大于层流润滑模型，其中青木弘-原田正躬湍流模型计算的水膜压力最大，Ng-Pan湍流模型和Constantinescu湍流模型计算的膜压相差不大，Hirs湍流模型计算的膜压最小。

4.2 不同湍流润滑模型下的雷诺数随偏心率的变化规律

图6为水润滑橡胶轴承在转速为600 r/min，间隙比为0.003时不同湍流模型下中截面的雷诺数随周向角度的变化规律。

从图6（a）、（b）、（c）和（d）可以看出，4种不同润滑模型下的雷诺数随偏心率的变化趋势一致，同时4种润滑模型在不同偏心率下的雷诺数相差极小，因此可以认为不同偏心率下湍流润滑模型对雷诺数的影响不大。同时，可以看出在承压区，雷诺数随偏心率的增大而减小，这是由于在承压区水膜厚度很薄，雷诺数在临界雷诺数Rec以下，流体主流态为层流;在非承压区，雷诺数随着偏心率的增大而增大，这是由于非承压区内的润滑膜较厚，雷诺数大于临界雷诺数，润滑流体的主流流态为湍流，湍流区内的流动状况较为复杂。

4.3 不同湍流模型下水润滑橡胶轴承的最大膜压和承载力随偏心率的变化

图7所示为转速为600 r/min，间隙比为0.003时，采用4种湍流模型计算得到的承载力和最大膜压随偏心率的变化分布。

从图7（a）、（b）可以看出，湍流模型的承载力明显大于层流模型;随着偏心率的增大，承载力和最大膜压逐渐非线性增大。

从图7（a）可看出，Hirs湍流模型下的承载力比青木弘-原田正躬的理论下的承载力小约9%，Ng-Pan润滑模型下的承载力与其3种理论下的承载力相差较大，但与层流下的承载力较为接近。这主要是由于Ng-Pan润滑模型不太适合用在低速，重载和大偏心下的运行工况下[28]。当偏心率在0.3～0.7之间时，4种湍流模型计算的承载力较为接近，当偏心率在0.7～0.9之间时，4种湍流模型计算的承载力差值较大。承载力由大到小的湍流模型依次为：Hirs模型，青木-原田模型，Constantinescu模型和Ng-Pan模型。从图7（b）可看出，青木-原田模型，Constantinescu模型和Ng-Pan模型计算的膜压差值不大，Hirs理论计算的膜压与这3种方法计算的差值较大。膜压由大到小的顺序依次为Hirs模型，青木弘模型，Constantinescu模型和Ng-Pan模型。

承載力和膜压呈现这种变化规律主要是由于

Constantinescu湍流理论没有考虑边界层的影响，而Ng-Pan湍流理论采用了湍流粘性系数，且考虑了边界层的影响，但其将流动按剪切流作线性近似处理，在大偏心和高雷诺数时有一定的局限性，且其只适合不可压缩流体膜的动压润滑，而Hirs是一种经验方法，有较大的缺陷，但青木弘-原田正躬湍流理论克服了Constantinescu和Ng-Pan方法的缺陷，寻找了一种新的壁面定律，其可以较为准确地计算轴承在湍流流态下的润滑特性。

4.4 不同湍流模型下承载力和最大膜压随转速的变化

图8为偏心率为0.6时，间隙比为0.003，采用4种湍流模型计算得到的承载力和最大膜压随转速的变化分布。

从图8（a）和（b）可以看出，随着转速的增大，

承载力和膜压近似线性增大，且采用湍流润滑模型计算的承载力和膜压远大于层流润滑。

从图8（a）可看出，4种湍流模型计算的承载力相差较大，仅在

300～500 r/min时，青木弘-原田正躬模型，Constantinescu模型和Ng-Pan模型计算的承载力较为接近。承载力由大到小的湍流润滑模型依次为：Hirs润滑模型，青木弘-原田正躬模型，Ng-Pan模型和Constantinescu模型。从图8（b）可看出，青木弘-原田正躬模型，Ng-Pan润滑模型和Constantinescu润滑模型计算的膜压较为接近，Hirs模型计算的膜压与这3种方法计算的差值较大。Constantinescu模型和Ng-Pan模型计算的膜压很小，在转速为300～500 r/min时几乎重合。这主要是由于随着转速的增大，雷诺数也增大，在高雷诺数状态时，流体流动很不稳定且动量交换很大，因此不考虑过渡层或将流动简单线性化处理候有较大的局限性，会导致承载力和膜压的差值随转速的增大而越来越大。

4.5 不同湍流模型下承载力和最大膜压随间隙比的变化

图9为偏心率为0.6时，转速为600 r/min，采用4种湍流模型计算得到的承载力和最大膜压随间隙比的变化分布。

从图9（a）和（b）可以看出，间隙比对承载力和膜压的影响都较大。随着间隙比的增大，承载力和膜压近似线性减小，且采用湍流润滑模型计算的承载力和膜压远大于层流润滑。

从图9（a）可看出，当间隙比从0.001增大到0.004时，承载力急剧下降，当间隙比从0.004增加到0.007时，承载力下降较为缓慢，同时承载力较小。青木弘-原田正躬模型，Constantinescu模型和Ng-Pan模型计算的承载力较为接近，Hirs模型计算的承载力与其它3种润滑理论计算的差值较大。承载力由大到小的湍流模型依次为：Hirs润滑模型，青木弘-原田正躬润滑模型和Constantinescu润滑模型。从图9（b）可看出，当间隙比为0.001～0.003时，青木弘模型，Ng-Pan模型和Constantinescu模型计算的膜压较为接近，Constantinescu模型和Ng-Pan模型计算的膜压在间隙比为0.001～0.003时几乎重合，Hirs模型计算的膜压与这3种方法计算的差值较大。这主要是由于Constantinescu湍流模型没有考虑边界层的影响，而Ng-Pan湍流模型考虑了边界层的影响，青木弘-原田正躬模型提出了一种新的壁面定律，它有很强的实用性。而Hirs是一种经验方法，它有较大的局限性。

5 结 论

1）4种湍流润滑模型下的衬层变形和最大膜压均大于层流润滑，其大小顺序为：青木弘-原田正躬模型>Ng-Pan湍流模型>Constantinescu湍流模型>Hirs湍流模型;不同偏心率下湍流润滑模型对雷诺数的影响不大。

2）水润滑橡胶轴承在高雷诺数工况下运行时采用湍流润滑模型计算的承载力和膜压远大于层流模型，层流假设不再适用其实际的运行工况;青木弘-原田正躬湍流润滑模型比Ng-Pan，Constantinescu和Hirs湍流模型更为合理。

3）随着偏心率和转速的增大，承载力和最大膜压均逐渐非线性和近似线性增大;随着间隙比的增大，承载力非线性减小，膜压近似线性增大。

对于高雷诺数运行工况下的水润滑橡胶轴承，采用青木弘-原田正躬湍流润滑模型比层流润滑理论有更为实际的指导意义，同时其也可为CFD仿真水润滑轴承润滑机理的研究和可靠性等方面提供一定的参考。

参考文献（References）：

[1] Taylor G I VIII.Stability of a viscous liquid contained between two rotating cylinders[J].Philosophical Transactions of the Royal Society of London.Series A，Containing Papers of a Mathematical or Physical Character，1923，223（605-615）：289-343.

[2]Taylor G I.The dispersion of matter in turbulent flow through a pipe[J].Proceedings of the Royal Society of London.Series A.Mathematical and Physical Sciences，1954，223（1155）：446-468.

[3]Taylor C M，Dowson D.Turbulent lubrication theory-application to design[J].Journal of Lubrication Technology，1974，96（1）：36-46.

[4]Constantinescu V N.On turbulent lubrication[J].Proceedings of the Institution of Mechanical Engineers，1959，173（1）：881-900.

[5]Constantinescu V N.Analysis of bearing operating in turbulent regime[J].Journal of Basic Engineering，1962，82：139-151.

[6]Ng C W，Pan C H T.A linearized turbulent lubrication theory[J].Journal of Basic Engineering，1965，87：675-688.

[7]Ng C W.Fluid dynamic foundation of turbulent lubrication theory[J].Wear，1964，7（4）：311-321.

[8]Elrod H G，Ng C W.A theory for turbulent fluid films and its application to bearings[J].Journal of Lubrication Technology，1967，89（3）：346-362.

[9]Hirs G G.A bulk-flow theory for turbulence in lubricant films[J].

Journal of Lubrication Technology，1973，95：137-146.

[10]青木弘，原田正躬.乱流域におけるジャーナル軸受の流体润滑理论[J].

润滑，1971，16（5）：348-356.

[11]Meinkai Ho，Vohr J H.Application of energy model of model of turbulence to calculation of lubricant flows[J].ASME，Journal of lubrication technology，1974，96（1）：95.

[12]张运清，张直明.一种紊流润滑理论分析新方法──复合型紊流模式理论[J].摩擦学学报，1995（3）：271-275.

ZHANG Yun-qing，ZHANG Zhi-ming.A new of theoretical analysis of turbulent lubrication using a combined model of turbulence[J].Tribology，1995（3）：271-275.

[13]王小靜，张直明，孙美丽.复合型紊流润滑理论模式的研究[J].摩擦学学报，2000（2）：127-130.

WANG Xiao-jing，ZHANG Zhi-ming，SUN Mei-li.A combined theory for turbulence in lubricating films[J].Tribology，2000（2）：127-130.

[14]Cabrera D L，Woolley N H，Allanson D R，et al.Film pressure distribution in water-lubricated rubber journal bearings[J].Proceedings of the Institution of Mechanical Engineers，Part J：Journal of Engineering Tribology，2005，219（2）：125-132.

[15]Frêne J，Arghir M，Constantinescu V.Combined thin-film and navier stokes analysis in high reynolds number lubrication[J].Tribology International，2006，39（8）：734-747.

[16]Shenoy B S，Pai R.Stability characteristics of an externally adjustable fluid film bearing in the laminar and turbulent regimes[J].Tribology International，2010，43（9）：1751-1759.

[17]Shyu S H，Jeng Y R，Chang C C.Load capacity for adiabatic infinitely wide plane slider bearings in the turbulent thermohydrodynamic regime[J].Tribology Transactions，2004，47（3）：396-401.

[18]王迎佳，刘敏珊，岑少起，等.层流紊流共存时径向滑动轴承热流体润滑性能分析[J].郑州大学学报（工学版），2013，34（5）：43-47.

WANG Ying-jia，LIU Min-shan，CEN Shao-qi，et al.Analysis of lubrication performance of hot fluid of journal bearing under the coexistence state of fluid with laminar flow and turbulence[J].Joumal of Zhengzhou University（Engineering Science），2013，34（5）：43-47.