基于HS-Small本构模型的银川地区深基坑开挖-降水过程数值分析

张卫兵，张刚柱，韩自刚，王 乐

(1.宁夏大学 土木与水利工程学院，宁夏 银川 750021；2.旱区现代农业水资源高效利用教育部工程研究中心，宁夏 银川 750021；3.宁夏建筑设计研究院有限公司，宁夏 银川 750021)

1 研究背景

由于计算机技术及土体本构关系的蓬勃发展，数值分析方法已经成为基坑工程有效的分析手段，其关键在于本构的选择和参数的设置[1]。

岩土工程应用最多的摩尔库伦模型是理想弹塑性模型，综合了胡可定律和Coulomb破坏准则，该模型对一般的岩土非线性分析结果是可靠的，广泛应用于模拟大部分岩土材料，但其不能考虑土体受应力历史的影响及区分加载和卸载模量。

Schanz等[2]于1998年提出硬化模型，其假设土体在卸载和重加载时是弹性的且区分加载和卸载模量，使用塑性理论，考虑了土体的剪胀性，引入了一个屈服帽盖弹塑性模型，可以模拟包括软土和砂土在内的不同类型的土体工程，已成为基坑开挖数值分析中最常用的模型之一，HS模型屈服帽盖示意图见图1。

实际上，土体刚度为完全弹性的应变范围很小，土在应变很小时具有很大的刚度，但随着应变的增大刚度会非线性地减小，土体刚度-应变曲线见图2。

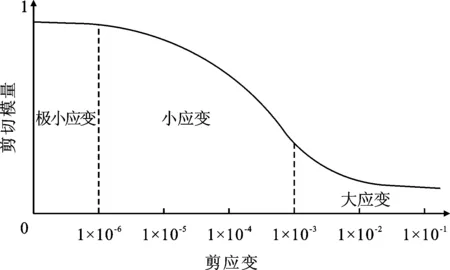
图2 土体刚度-应变曲线

为了描述土的这种性质，Benz[3]根据Atkinson关于土体小应变试验的研究成果，提出了小应变HS-Small模型，该模型是对HS模型的修正，即为小应变弹塑性模型，在HS模型基础上增加了描述小应变刚度行为的小应变剪切模量G0和剪切应变水平γ0.7，使得该模型能表征土的小应变及刚度衰减性，能给出更为可靠的位移和计算结果[4]，因而被越来越多地应用于考虑小应变的岩土数值分析中。宋二祥等[4]利用HS-Small和HS模型模拟基坑变形，HS-Small模拟结果较HS模拟结果更加吻合实际。王卫东等[5]做了关于上海典型土层HS-Small参数试验，并在基坑工程数值分析中加以验证，取得较好的数值结果，并反分析得出一套上海地区HS-Small参数的取值表。梁发云等[6]通过对上海地区典型软土HS-Small模型参数的试验研究，得出割线刚度、切线刚度及卸载加载刚度之间的数量关系，与王卫东等[5]的研究结果较为一致。郑刚等[7]利用HS-Small模型研究基坑开挖引起邻近既有隧道变形的影响区，得出坑外隧道变形的影响区大致可简化为直角梯形形状，张玉伟等[8]提出的椭圆形影响区与其较为一致，可用于预估隧道可能产生的变形。

近几年来，银川地区由于城市工业用水量的不断增加，引起地下水位持续下降，使得土体产生沉降以及土性、结构的变化[9]。银川地区鲜有采用HS-Small本构对深基坑数值模拟的实例，本文利用HS-Small模型对该地区某地下车库基坑的开挖-降水过程进行数值分析，以探讨该地区基坑开挖-降水变形规律、锚杆及土钉受力特征。在此基础上，利用反分析法[10-11]，得出一套银川地区类似工程HS-Small模型的参数表，供该地区基坑工程数值模拟、设计与施工参考。

2 工程概况

2.1 工程位置及规模

建筑场区位于银川市金凤区，西靠亲水大街、南对凤凰公园。

基坑平面尺寸为120 m×81 m(长×宽)。北距主办公楼32.2 m，东、西距1#、2#、3#、4#院21.2 m，车库坡道北距3#、4#院12.28 m，南侧开阔。车库地下2层部位基坑开挖深度9.5 m，地下1层部位基坑开挖深度6.6 m，地下车库坡道由6.6 m(地下1层)缓坡至自然地面(见图3)。

图3 基坑位置、规模及监测点布置

2.2 场区地层、水文及降水

(1)层素填土(Q4ml)：本层以黄褐～灰褐色为主，以粉质黏土(可塑)、粉土(稍湿，稍密)为主，平均厚度约3.4 m。

(2)层粉质黏土(Q4al+l)：黄褐～灰褐色，可塑状态，中等压缩性，平均厚度约1.4 m。

(3)层粉土(Q4al)：褐黄色～黄褐色，湿，中密～密实状态，中低压缩性土，平均厚度约2.8 m。

(4)层粉细砂(Q4al)：黄褐色～灰褐色，饱和，上部以粉砂为主，中下部主要为细砂，中低压缩性，未穿透，最大揭露厚度29.55 m。

实测地下水静水位埋深约为4.3 m，潜水类型，含水层主要由粉、细砂构成。水位动态年变化幅度为1.00～1.50 m。

共布降水井26口，降水井深30、25 m。其中基坑内南北轴线上布置2口降水井，基坑外边缘布置24口降水井。

2.3 监测点布置

基坑地下水位下降引起的建筑物周围地面沉降的地基沉降问题已成为工程建设中的重大环境灾害问题，本基坑周边(除南侧)紧邻公路和办公楼，因此基坑开挖-地下水位下降的监测和影响性分析显得尤为必要，基坑监测点(以JCD表示，监测内容包括基坑坑顶水平、竖向位移)及周边建筑物测点(以D标记，监测内容包括建筑物沉降)布置详见图3。

2.4 锚钉联合支护形式

本基坑支护采用锚杆-土钉联合支护方案，土钉能加固和补强土体，起到加筋作用，减少基坑侧壁土压力。锚杆为主动受力构件，能很好地控制变形，支护形式见图4。喷射钢筋混凝土面层厚度为100 mm，挂单层φ6@150×150的钢筋网。

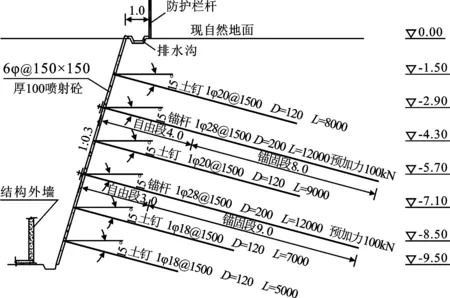
图4 基坑支护典型剖面图(高程及标注单位：m；其他单位：mm)

3 数值模型的建立

3.1 边界条件的选取

根据该基坑工程的实际尺寸，以边坡规范为依据，取土层边界50 m×310 m×270 m(高×长×宽)。初始水位为-4.3 m，坑内降水至-10.5 m。模型底部施加固定约束，四周施加法向约束。基础最初属性为素填土，建筑施工时改变属性为混凝土。

3.2 土体本构模型的确定及计算参数

按前文所述各模型的适用性，本文选用HS-Small本构模型对该基坑开挖-降水过程进行数值模拟。

数值模拟参数的确定直接影响模拟计算结果，是模拟过程的关键环节。HS-Small模型参数包含了11个模型参数和2个小应变参数。模型参数为：有效黏聚力c′、有效内摩擦角φ′、泊松比ν、剪胀角ψ、三轴固结排水剪切试验的参考割线模量E50、固结试验的参考切线模量Eoed、三轴固结排水卸载再加载模量Eur、与模量应力水平相关的幂指数m、参考应力p、破坏比Rf、正常固结条件下的静止侧压力系数K0；小应变参数为：初始小应变剪切模量G0，剪切应变水平γ0.7，即为割线模量减小到70%G0时的应变水平。

以勘察报告为依据的5个一般参数：容重γ、饱和容重γsat、孔隙比e0、渗透系数k、压缩模量ES1-2；以勘察报告为依据的2个模型参数：有效黏聚力c′、有效内摩擦角φ′；剪胀角ψ一般为有效摩擦角减去30°，黏性土一般取0°[4,12]。泊松比ν对于大部分土体可取为0.2[14]。根据宋二祥等[4]和Janbu[13]的研究，对于砂土和粉土，应力水平幂指数m一般可取为0.5；对于黏性土，m的取值范围为(0.5～1)。参考压力p一般取100 kPa，静止侧压力系数K0=1-sinφ＇[12]。破坏比Rf一般取为0.9[12](为简略，表中略去)，E50、Eoed、Eur的取值参考模型手册[4]、王卫东等[5,14]及Brinkgreve等[12]通过试验得出的结果，对于砂性土，E50=Eoed=ES1-2，Eur=3E50，而黏性土大约有E50=1.2Eoed=1.2ES1-2，Eur=3E50。两个小应变参数，根据Hardin和Black等的研究，有经验公式G0=33(2.97-e0)2/(1+e0)，e0为土体初始孔隙比；黏性土γ0.7按γ0.7=0.0001+5×10-6Ip×(OCR)3，砂性土γ0.7一般可取为0.0002，且其变化范围很小[14-15]。在此基础上，以实测基坑位移反演确定参数[16-17]，具体模拟参数如表1、2所示，参考压力p均为100 kPa(表中略)。

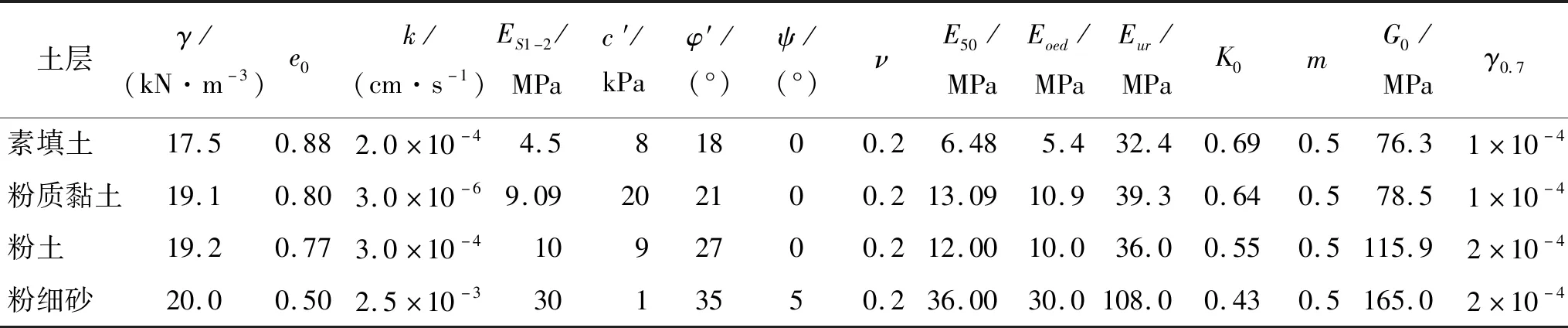
表1 土体HS-Small模型计算参数

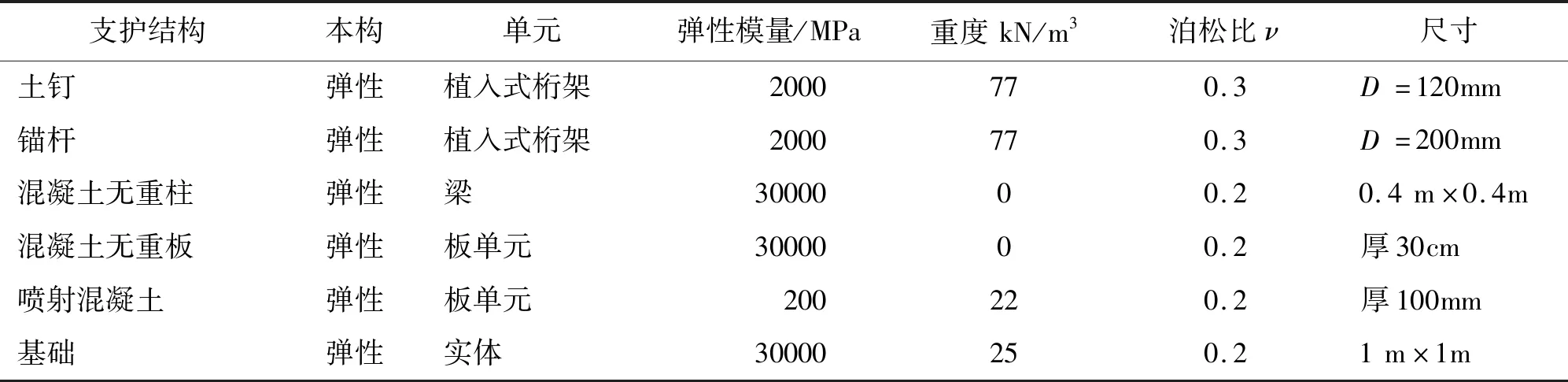
表2 构件参数

3.3 数值模型网格划分

利用3D实体单元模拟土体，计算稳定，精度高。1D植入式桁架单元模拟土钉和锚杆，吻合两者的受力状况。1D梁单元模拟柱，2D板单元模拟混凝土面层、建筑物板。基坑处网格尺寸为1.5 m，模型边界处网格尺寸为5.5m，数值模型及网格划分如图5。

3.4 定义施工工况

施工工况尽可能与实际保持了一致，利用基坑内每层土节点水头进行降水，与降水井降水效果相似，分层开挖深度依照支护位置选定。建筑单柱荷载依据地基承载力特征值和基础面积取为100 kN，锚杆施加预应力为100 kN，计算施工工况如表3所示。

4 结果分析

4.1 基坑坑顶水平、竖向位移分析

图6为基坑坑顶水平、竖向位移数值计算结果。由图6(a)可知，基坑开挖-降水引起的变形主要是基坑底部土体的上升隆起，最终隆起量达到11 mm；基坑侧壁的应力方向均指向基坑内部，周围土体的变形呈现出明显的圆弧滑动面，土体变形区域呈“W”形分布。这是由于基坑侧壁除受水土压力外，还受到基坑开挖后侧向应力释放、圆弧滑动面土体下滑产生的附加荷载及周围建筑物应力场的共同作用。

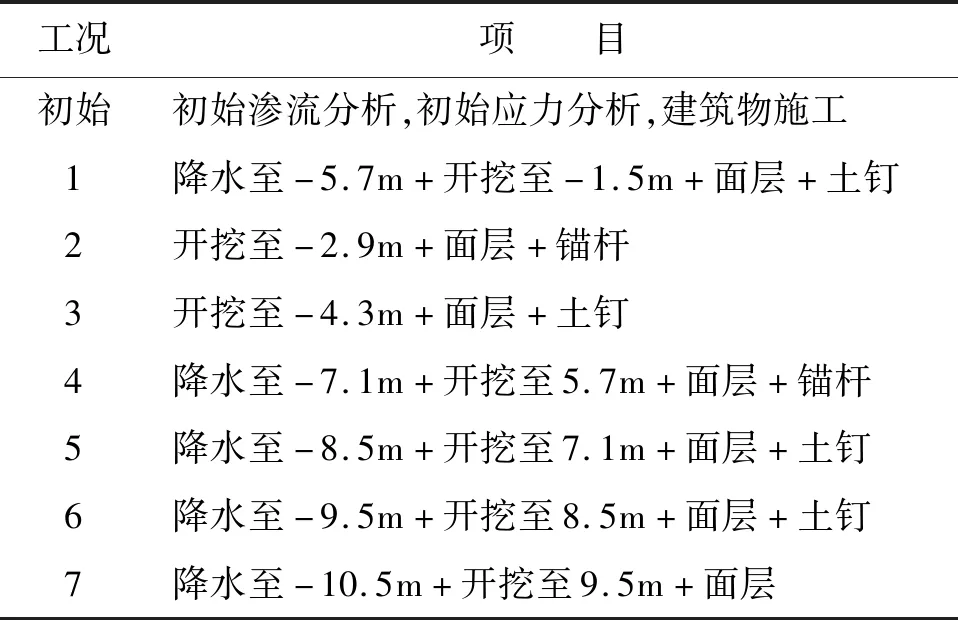
表3 施工工况

将基坑坑顶水平、竖向位移与模拟结果进行了对比，如图6(b)～6(g)。模拟结果和监测位移吻合较好，随着开挖深度的增加，水平和竖向位移均增大。在工况4之前基坑设置2道土钉+2道锚钉，位移变形较缓，工况4之后，基坑只设置2道土钉。可以把工况4之前的支护看作锚钉联合支护形式，之后的看作土钉墙支护形式。在工况4之后，水平和竖向位移变化速率加快，一方面是由于锚杆联合支护结构控制变形能力优于土钉支护，不难发现，在两种支护形式界面处(工况4)，变形速率加快；另一方面基坑开挖-降水的持续进行，孔压减小，有效应力增加，使得基坑周边土体沉降增大；同时由于土体侧向应力释放，圆弧滑动面不断发展，产生附加荷载增大，这三者共同使得后续的基坑变形速率加快、变形量加大。

图5 数值模型及网格划分示意图

图6 不同工况基坑坑顶水平、竖向位移监测值及模拟值曲线

图7为基坑水平向位移云图及现场图，其中水平位移云图与现场土体破坏位置的对比如图7(a)、7(c)和7(d)所示，施工现场基坑坑顶附近裂缝如图7(b) 所示，图7(a)中max、min位置分别对应图7(c)、7(d)中土体破坏位置。对比结果表明，土体实际破坏位置和计算最不利位置极为吻合，说明HS-Small模型用于银川典型土层数值分析的正确性和有效性，同时验证了本文数值分析的正确性。由图7(c)、7(d)可知，基坑实际破坏位置位于阳角处，这是由于基坑开挖过程中，阳角处土体应力单元的σ2和σ3同时释放，相比其他位置土体单向应力释放，此处侧向约束减小更多，浅层土体破坏引起喷射混凝土破坏。此外，由于建筑物荷载在地基边角处会产生力集中现象[18]，本基坑工程阳角恰与周边建筑物边角相邻，已有建筑物荷载在基坑阳角处产生应力集中，由此导致了基坑阳角处变形增大，稳定性降低，进而产生破坏，实际破坏位置和计算结果一致。

4.2 基坑peck沉降曲线分析

第1次开挖后基坑沉降曲线与peck沉降曲线较为吻合，如图8所示，说明数值模拟符合基坑工程理论。基坑顶1.5 m范围内出现隆起，初步分析是由于基坑开挖后，基坑隆起带动周边土向上移动，隆起位移约为0.4 mm。据实测资料，JCD2第1次开挖后隆起0.2 mm，模拟结果与监测数据接近，且隆起量很小，不影响数值分析的结果，随着基坑的开挖，隆起消失。

图7 基坑水平向位移云图及现场图

图8 基坑开挖peck沉降曲线

4.3 基坑地下水位下降及周边建筑物沉降分析

对基坑周边建筑物的沉降过程进行数值模拟预测，可有效预防和控制由于基坑开挖和地下水位下降引起的环境灾害[19]。基坑采取边降水边开挖的作业方式，数值模拟中初始水位为-4.3 m，基坑内最低水位降至-10.5 m，基坑及其周边地下水位分布云图见图9，基坑周边建筑物沉降主要取决于地下水位的变化。

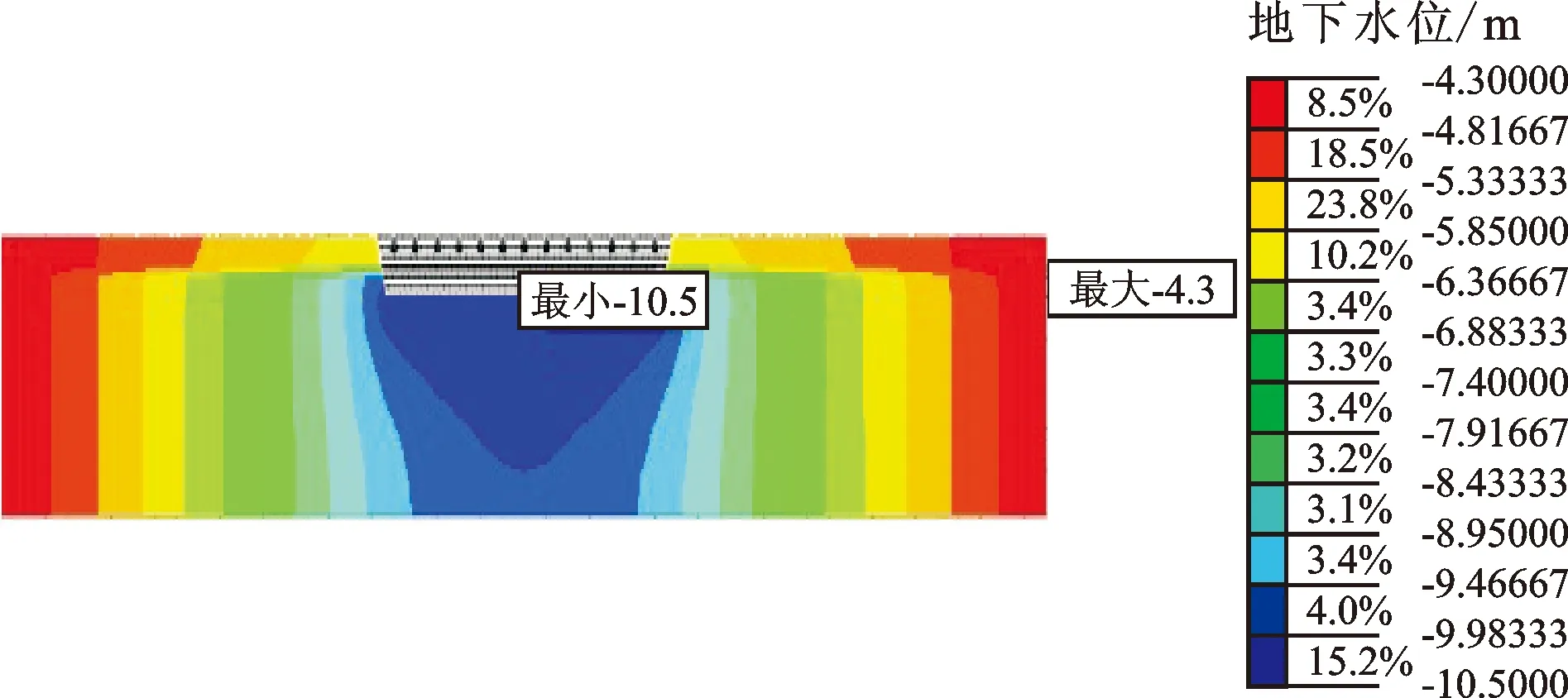
图9 基坑及其周边地下水位分布云图

图10为不同工况基坑周边建筑物沉降监测值及模拟值曲线。

由图10可知，建筑物沉降观测值与模拟值吻合较好，误差在2 mm左右，表明图9所示的基坑最终地下水位下降与实际水位状况相吻合。

由图10(a)发现，D3监测点沉降比较特殊，在工况7时抬升了1.5 mm，此时基坑已开挖到坑底，基坑水位也下降至-10.5 m，D3监测点附近的JCD16下沉了10.9 mm。将该过程看成排水固结试验，围压减小，D3却出现了抬升，这可能与建筑刚度影响有关[7,18]，然而与D3对称的D8测点在工况7是下沉的，由此判断监测点可能受到施工运输车辆挤压造成抬升或监测产生误差，但该误差在可控范围内。图10(b)中的D6、D8、D9监测点在工况4时出现抬升的原因可能与D3类似。

4.4 锚杆及土钉受力分析

基坑支护采用锚钉联合支护，锚杆和土钉典型轴力分布如图11和12所示。

图12 土钉典型轴力图(单位：kN)

由图11(a)～11(c)可知，锚杆轴力随着基坑开挖深度增加而加大；由图11(c)～11(d) 可知，锚杆轴力沿长度方向呈曲线分布，轴力最大值位于承压板处，在锚固段起始位置和承压板处较为接近，从锚固段开始，轴力逐渐减小。第1层锚杆轴力小于第2层锚杆轴力，相应控制变形能力较弱，这与其(第1层锚杆)处于素填土中有关系，素填土中粉质粘土分布不均匀，提供锚固力不稳定，更重要的是，基坑开挖后侧向应力释放使得圆弧滑动面土体下滑产生附加荷载，该附加荷载下部大于上部，因此使得下部锚杆轴力大于上部锚杆轴力。综上，锚杆控制变形能力与所处位置有关。

比较图12(a)与图12(b)发现，锚钉联合支护中土钉轴力分布和单纯土钉支护轴力有所不同，锚钉支护中土钉轴力类似于S型曲线，轴力最大值约位于沿土钉长度3/4位置处，这是由于锚杆的存在改变了单纯土钉的受力机理，单纯土钉轴力分布为中间大、两头小，但是无论是锚钉支护还是单纯土钉支护，土钉轴力的分布规律依然是中间部位或其附近处轴力大于两端部位轴力。土钉之所以出现中间部位或其附近大两头小，这是由于基坑变形过程中，土钉之间会形成土拱，土钉起到拱脚的作用，土钉承担了一部分变形，同时由于潜在滑移面的存在，使得土钉中部承受变形更多，从而使得土钉中间部位或其附近轴力较大。

5 结 论

本文通过对宁夏银川地区某地下车库基坑开挖-地下水位下降进行了数值模拟计算，得出以下结论：

(1)随着基坑开挖深度的增加，基坑水平、竖向位移增大，基坑顶部阳角处变形较大，因此在施工过程中应及时完成该部分的支护结构，宜适当加密布置土钉。

(2)锚杆轴力随开挖深度的增加而加大，锚钉联合支护结构控制变形能力较好，锚杆控制变形能力与所处位置有关；在锚钉支护形式和土钉支护形式界面处变形差异较大，锚钉支护中土钉轴力表现为轻微S型曲线，轴力最大值约位于沿土钉长度3/4位置处，不同于单纯土钉支护结构中轴力中间大、两头小的分布规律，但轴力分布规律是一致的，土钉中部或其附近轴力大于两端轴力。

(3)随着开挖和持续降水，周边建筑物沉降缓慢增加且最终沉降小于警戒值。

(4)小应变HS-Small模型模拟结果和实测数据吻合较好，并通过反分析获得一套银川地区典型土层模型参数的取值表，以供类似工程参考。