刹车片表面缺陷的图像检测方法
韩志玮,高美凤
(1. 江南大学 轻工过程先进控制教育部重点实验室,江苏 无锡 214122;2. 江南大学 物联网工程学院,江苏 无锡 214122)
引言
刹车片是汽车制动系统重要的安全部件,它的质量直接影响到刹车系统的性能。在压制生产的过程中,刹车片的摩擦块表面容易出现凹陷、毛刺等缺陷。目前生产厂家都是靠人工目测筛选摩擦面出现缺陷的产品,但是人工检测方法效率低下,并不能适应于大规模的生产环境。随着机器视觉和图像处理技术的发展,基于机器视觉的自动检测方法正逐渐替代人工检测法,得到了广泛的应用。江恒等[1]设计了基于机器视觉技术的自动检测微光夜视仪整机的系统;宋丽梅等[2]基于图像处理技术,提出了一种改进梯度幅值相似性的包装缺陷检测算法;魏永杰等[3]提出累积梯度的图像法检测裂缝缺陷的方法;曾强[4]等设计了一种基于机器视觉技术的刹车片轮廓缺陷检测方法,创建匹配模板实现对图像的快速对准,再利用差影法检测轮廓缺陷;费成等[5]设计了基于机器视觉的汽车刹车片自动检测系统,完成了图像获取、图像校准、图像定位、尺寸测量、缺陷标示、字符识别等任务。
目前现有的针对刹车片表面缺陷的自动检测方法基本上是基于模板匹配的检测方法,该方法需要提前制作标准刹车片样本的模板用于比对分析。但由于市面上刹车片种类繁多,各个型号的刹车片外观形状及表面纹理情况均不相同,为每一种刹车片都制作标准模板,费时费力。由于刹车片表面粗糙不平滑,存在复杂不规则的纹理情况,在复杂背景纹理的情况下检测缺陷有一定的难度。灰度共生矩阵[6](gray level co-occurrence matrices,GLCM)是一种提取纹理特征的有效方法,能够应用于织物图像的纹理分析[7]、医学图像的目标分割[8]、工业钢轨表面缺陷提取[9]等。聚类分析是一种数据分析的过程,可将相似性的数据进行聚类,是一种无监督的数据分类方法[10],密度聚类[11](density-based spatial clustering of applications with noise,DBSCAN)是聚类分析的一种方法,可识别任意形状的数据簇。将纹理信息提取出来后,可利用聚类分析的方法分析纹理数据,从而达到发现异常数据的目的。
为了避免模板匹配法繁琐的模板制作过程,本文提出一种基于机器视觉的结合灰度共生矩阵和密度聚类的刹车片表面缺陷检测新方法,利用灰度共生矩阵提取刹车片正常纹理及缺陷纹理的特征,进而通过密度聚类分析纹理数据。该方法能够适用不同类型的刹车片表面缺陷检测,根据刹车片摩擦面自身的纹理特征及缺陷部位的特征自动检测缺陷。
1 灰度共生矩阵
灰度共生矩阵是由Haralick[6]等人于1973 年提出,它是一种通过研究灰度的空间相关特性来描述纹理的常用方法,其描述为在θ 方向上,相隔距离d 的一对像素分别具有灰度值i 和j 出现的概率,记为 p(i,j;d,θ)。灰度共生矩阵的构建需要考虑4 个构造因子的取值,包括方向(θ)、灰度级(N)、滑动窗口及步长(d)。灰度共生矩阵共有14 个统计特征参数,这些特征能够很好地描述纹理图像中像素之间的相邻关系。这14 个特征包括角二阶矩(angular second moment,ASM)、对比度(contrast,CON)、相关性(correlation,COR)、逆差矩(inverse difference moment,IDM)、熵(entropy,ENT)、方 差(variance,VAR)、均 值 和(sum of average,SOA)、方差和(sum of variance,SOV)、差方 差(difference of variance,DOV)、和 熵(sum of entropy,SOE)、差熵(difference of entropy,DOE)、最大相关系数(maximal correlation coefficient,MCC)和2 个相关性度量参数(information measures of correlation,IMOC)。其中后3 个参数是对前11 个参数的进一步描述,因此后3 个参数很少被采用[12]。由于不同的特征参数表示不同的纹理特征,需要确定灰度共生矩阵构造因子的取值并从11 个参数中选取最适合用于分类的特征参数。首先通过角二阶矩、熵、逆差矩、对比度这4 个最有描述能力的特征参数[13]确定构造因子的选取,再利用线性相关性确定具有分类能力的特征参数。
1.1 构造因子的选取
根据刹车片摩擦面图像的实际纹理情况,在不同构造因子的情况下分别计算3 种不同类型样本的4 个特征参数的值。
1) 角二阶矩
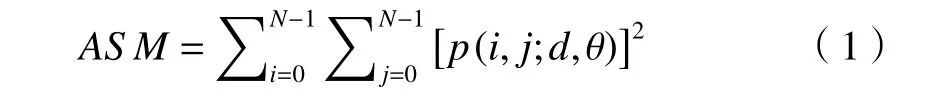
它是灰度共生矩阵像素值的平方和,反映图像灰度分布均匀程度及纹理粗糙程度。
2) 熵
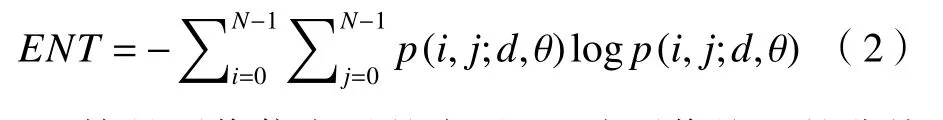
熵是图像信息量的度量,反映图像纹理的非均匀程度和复杂程度。
3) 逆差矩
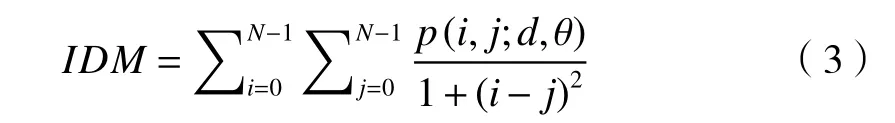
逆差矩反映图像的局部平稳性。
4) 对比度
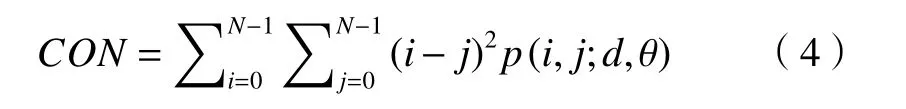
对比度是对图像局部灰度变化量的描述,反映图像的清晰度和纹理清晰程度。
通过实验结果的分析确定各个构造参数的取值。样本图像像素为250×250,这3 种样本如图1所示,其中(a)为正常样本,(b)为含凹陷缺陷部位的样本,(c)为含毛刺缺陷部位的样本,缺陷部位由黑色方框框出。从图中可以看出,凹陷部分与正常部分有明显的差别,凹陷部分纹理情况比较单一,且灰度值明显低于正常部分;而毛刺部分较正常部位区别不明显,只见灰度值稍低于正常部位,且一般情况下凹陷部位缺陷面积较小,毛刺部位缺陷面积会比较大。

图 1 正常纹理及含缺陷纹理样本Fig. 1 Normal and defective texture samples
1.1.1 方向参数的选择
方向参数θ 为灰度共生矩阵相邻像素之间的 角 度 关 系。常 用 的θ 角 度 包 括0°、45°、90°、135°。当纹理呈现一定方向性时,灰度共生矩阵会在某个方向上差异较大[14]。固定滑动窗口尺寸和灰度级均为16,步长为1,计算3 个不同类型样本的4 个不同方向的4 个特征参数的值之间的方差,实验数据如表1 所示,由表中可见,不同方向上数据的方差较小,基本上约等于零。方差反映了数据的离散程度,方差的值越小说明数据离散程度越小,数据之间差异不明显,故θ 角度影响较小,说明刹车片摩擦面纹理不具有特定的方向性。为了减小计算的复杂度与计算时间,本文θ 直接取值为0°。
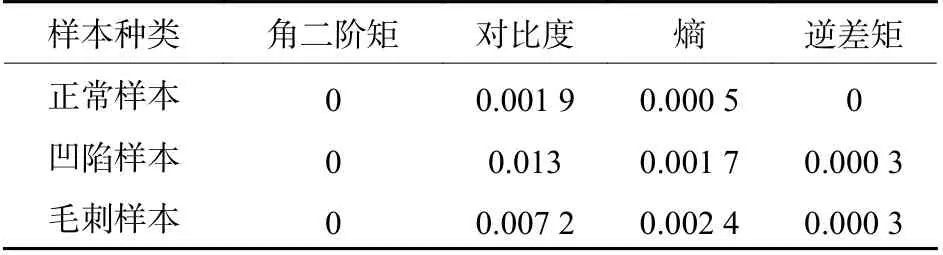
表 1 正常、凹陷、毛刺3 种样本在不同方向的特征值之间的方差Table 1 Variance between eigenvalues of normal,concave,and burr samples in different directions
1.1.2 灰度级的选择
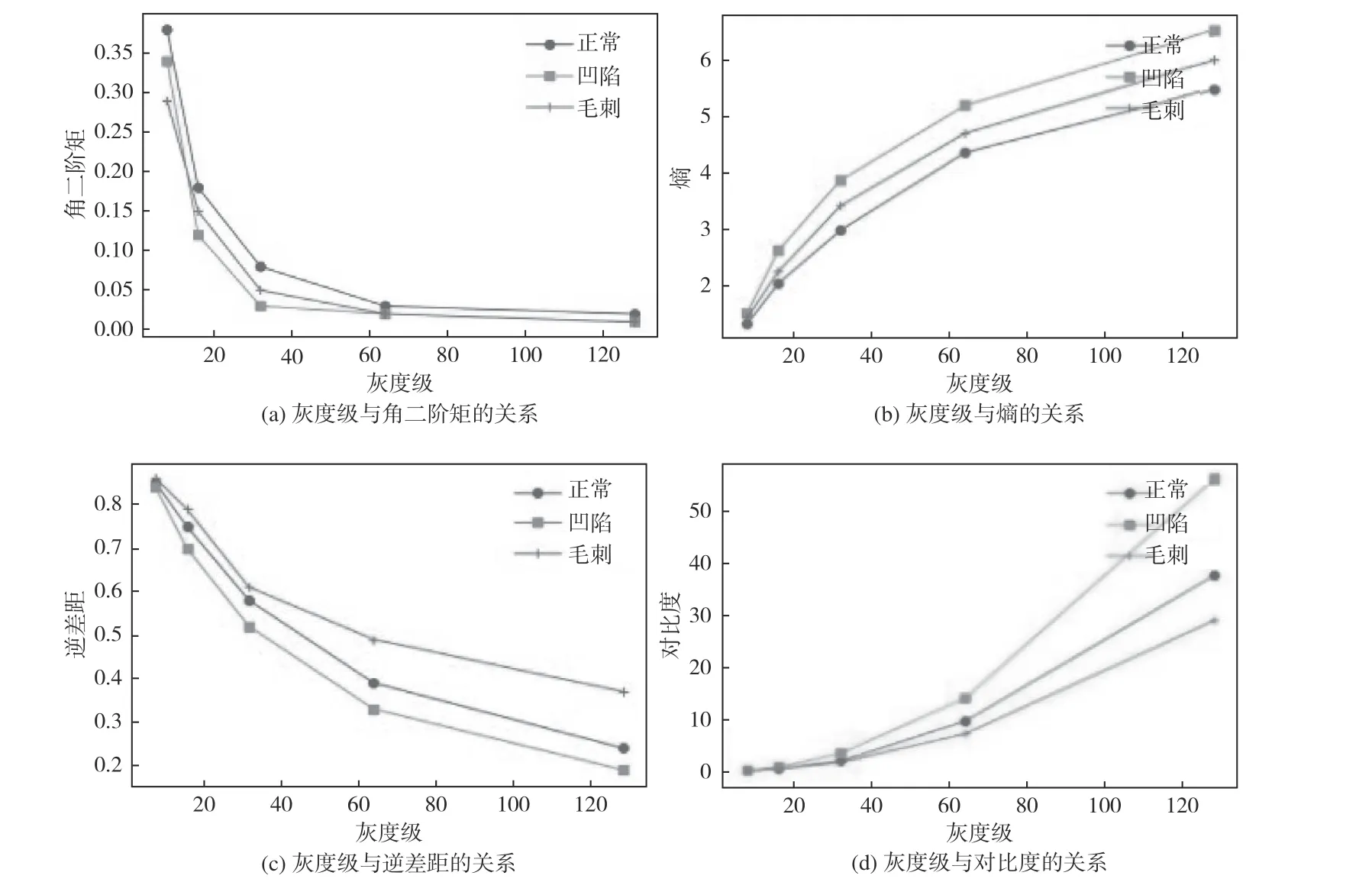
图 3 特征值—灰度级的关系曲线Fig. 3 Relation curves of eigenvalue-gray level
灰度级为图像压缩后最大的像素等级,它指定生成的灰度共生矩阵的大小[15]。固化滑动窗口尺寸为16、步长为1、角度为0°,灰度级取值8、16、32、64、128,分别进行不同灰度级下特征值的计算,得到特征值—灰度级曲线关系如图3 所示。从实验结果看出,当灰度级为8 时,熵、逆差矩、对比度3 种特征值之间差距较小,只有角二阶矩一个特征参数能够明显地区分;而当灰度级逐渐增大,不同样本的熵、逆差矩、对比度3 种特征值之间差距逐渐增大,能够区分不同的样本;当灰度级达到64 及以上时,角二阶矩特征的变化逐渐不明显,此时失去区分各个样本的能力。由于灰度级较大会增加灰度共生矩阵的维数,从而引起运算时间增加,故灰度级应尽可能缩小。为了使尽可能多的特征参数能够区分不同的样本,同时又考虑运算时间成本的问题,本文最终确定灰度级的取值为16。
1.1.3 滑动窗口尺寸的选择
滑动窗口尺寸为遍历图像的窗口大小,即为要划分若干小窗口的尺寸。固化灰度级为16、方向为0°、步长为1,取滑动窗口尺寸为8、12、16、20、24、32、48、64,计算不同窗口尺寸下3 种不同样本的特征值,实验结果如图4 所示。由图中可见,在窗口尺寸为16 至48 之间时,大部分特征值之间差距较大,易于区分;对于缺陷样本而言,当滑动窗口大于24 时,各个特征值的变化极小。经统计,样本中凹陷尺寸像素大小约为30×30 左右,由于凹陷缺陷部位较小,当滑动窗口尺寸逐渐增大,滑动窗口内包含凹陷部分以外的正常部分也逐渐变多,为了尽可能准确地表征凹陷部分纹理特征,准确的滑动窗口的尺寸应尽可能的小,最终选取的滑动窗口尺寸为16。
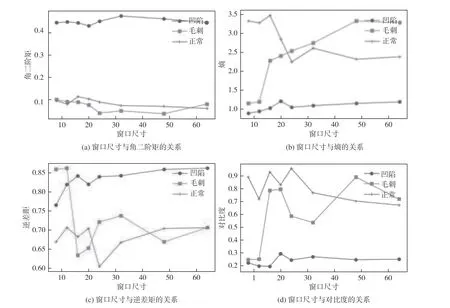
图 4 特征值—滑动窗口尺寸的关系曲线Fig. 4 Relation curves of eigenvalue-sliding window size
1.1.4 步长的选择
步长的值会影响灰度共生矩阵特征参数的计算结果,步长的取值不宜过大,步长过大会造成两像元之间的像素信息丢失增大,影响纹理特征的准确性[16],在步长分别为1~8 及灰度级为16、滑动窗口为16×16、方向为0°的情况下构造灰度共生矩阵,计算4 个常用特征参数,构造步长与特征量之间的关系曲线如图5 所示。从图中可以看出,大部分特征在步长大于3 的时候变化比较平缓,说明此时提取的特征比较稳定,且不同样本之间特征值差异明显,能更好地用来做区分,因此本文选取的步长为4。
1.2 特征参数的选取
Pearson 相关系数[17]是度量变量之间的相关性的常用准则,能表示特征之间的相关程度。通过计算Pearson 相关系数可以筛选出适于作聚类分析的特征。Pearson 相关系数定义为2 个变量之间的协方差和标准差的商,即:

式中:cov(X,Y)表示变量X 和Y 的协方差; σX和σY分别为变量X 和Y 的标准差;ρ 为变量X 和Y 的Pearson 相关系数。ρ 的绝对值越大,表明2 个变量之间的相关性越强。
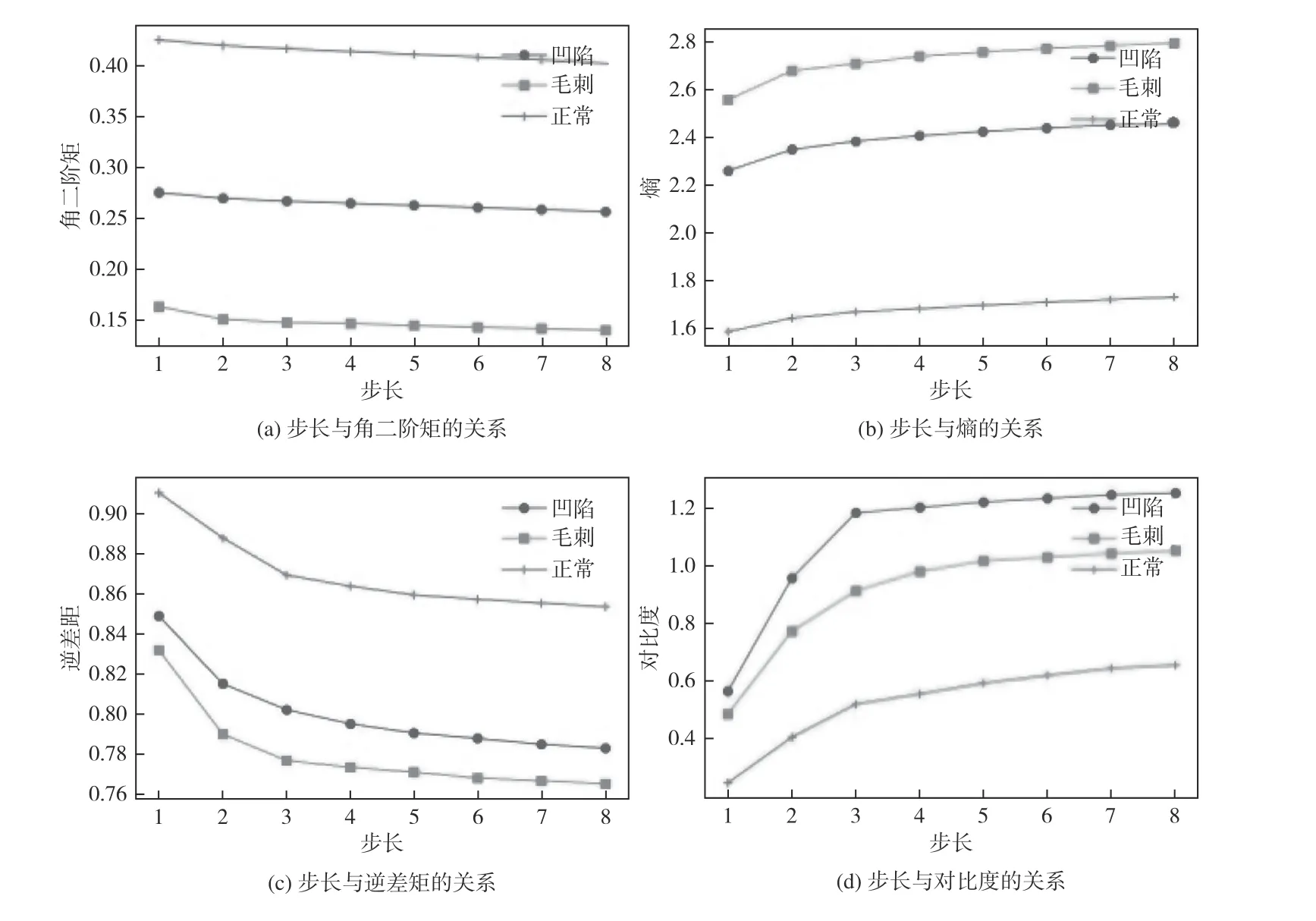
图 5 特征值—步长的关系曲线Fig. 5 Relation curves of eigenvalue-step
采用该方法计算11 个特征中每2 个特征之间的相关系数并取绝对值,得到的相关系数矩阵如表2 所示。本文将线性相关系数阈值设置为0.85,两个特征参数之间的相关系数大于0.85 的即认为有较强的相关性,否则认为相关性较低。分析表2中的数据,可将特征参数分为6 组,每组内相关性较强,各组之间相关性较弱。第1 组包括角二阶矩、熵、逆差矩、和熵、差方差;第2 组包含均值和、和熵;第3 组包含逆差矩、和熵、差方差、差熵;第4 组包含对比度、差熵;第5 组包含方差、方差和;第6 组包含相关性。从每组中各选出一个特征参数,这些参数之间的相关性较低,适合作为分类依据。最终选择的结果为角二阶矩、均值和、逆差矩、对比度、方差和、相关性。
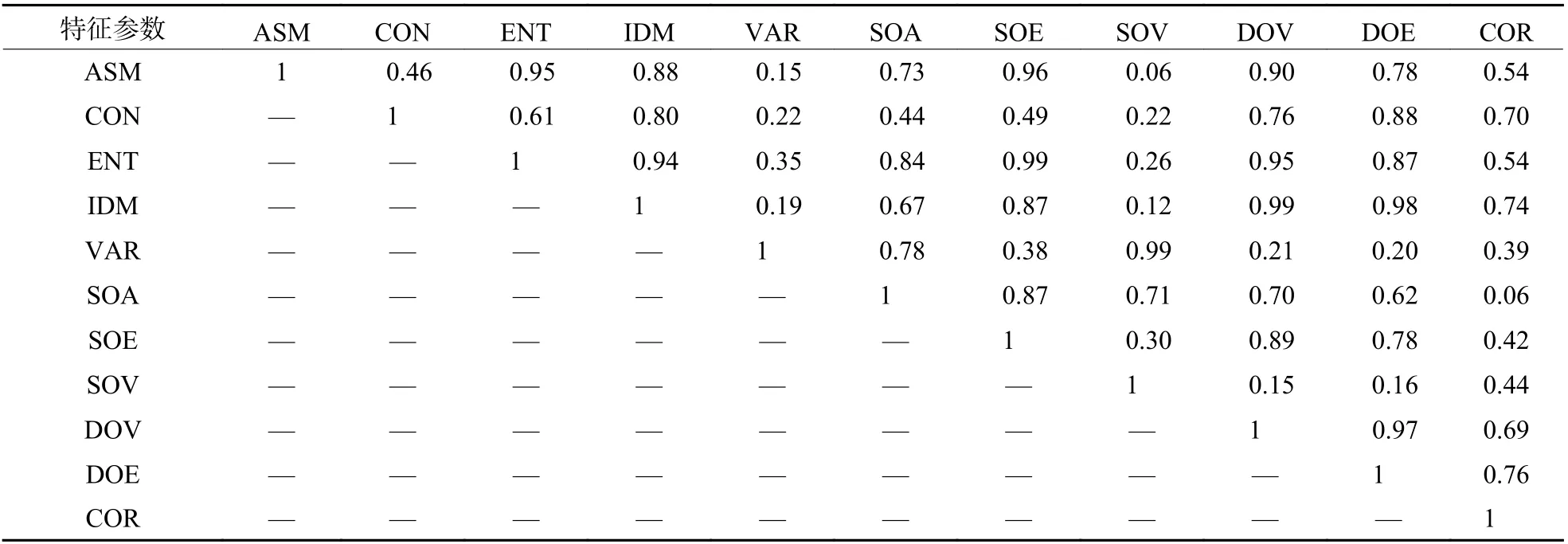
表 2 特征参数之间的线性相关矩阵Table 2 Linear correlation matrix between characteristic parameters
2 密度聚类
聚类分析能够发现给定数据集中发现数据元素之间的潜在联系。DBSCAN 算法是基于密度的空间聚类算法中的典型代表,能够在簇数未知的情况下,完成对形状不规则的、具有噪声的数据集的聚类。经典的DBSCAN 聚类算法需要人为手动设定Eps 和Minpts 参数[18],因而根据数据集自身的空间分布特性,利用K-平均最邻近算法[19](Kaverage nearest neighbor,K-ANN)和数学期望法自动确定Eps 和Minpts 参数集。
采用K-平均最近邻法生成Eps 列表,通过计算数据集D 的距离分布矩阵[20]:
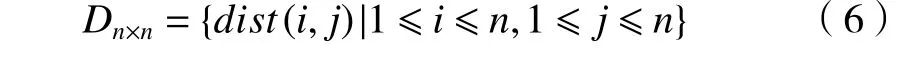
式中:n 为数据集D 中对象的数量; dist(i,j)为数据集D 中对象i 与对象j 之间的距离。

依次求出每个Eps 参数对应的Eps 邻域对象数量,并计算所有对象的Eps 邻域对象数量的数学期望值,作为数据集D 的邻域密度阈值Minpts 参数,表示为

式中Pi为第i 个对象的Eps 邻域对象数。
Eps 和Minpts 参数列表生成后,根据聚类簇数与K 值的关系自适应确定最优参数。利用每个K 值对应的Eps 和Minpts 值对数据集D 进行聚类分析,统计不同K 值下所生成的簇数,得到聚类簇数与K 值的关系。当簇数随着K 值趋于稳定(连续4 个以上不同K 值情况下的簇数不变)时,认为此簇数为最佳聚类簇数,取该簇数对应的最大的K 值即为最佳K 值,该K 值对应的Eps 和Minpts值为自动确定的最佳参数值。
由于刹车片摩擦面缺陷主要存在两种情况,较小的凹陷部位和较大的毛刺部位,在聚类分析时,两种不同的缺陷部位产生的数据结果不一样。正常样本及两种不同缺陷样本聚类簇数与K 值的关系如图6 所示,从图中可以看出,只有毛刺样本的簇数在随着K 值的增大而出现两次稳定区间,而正常样本及凹陷样本最佳聚类簇数始终只有1 类。
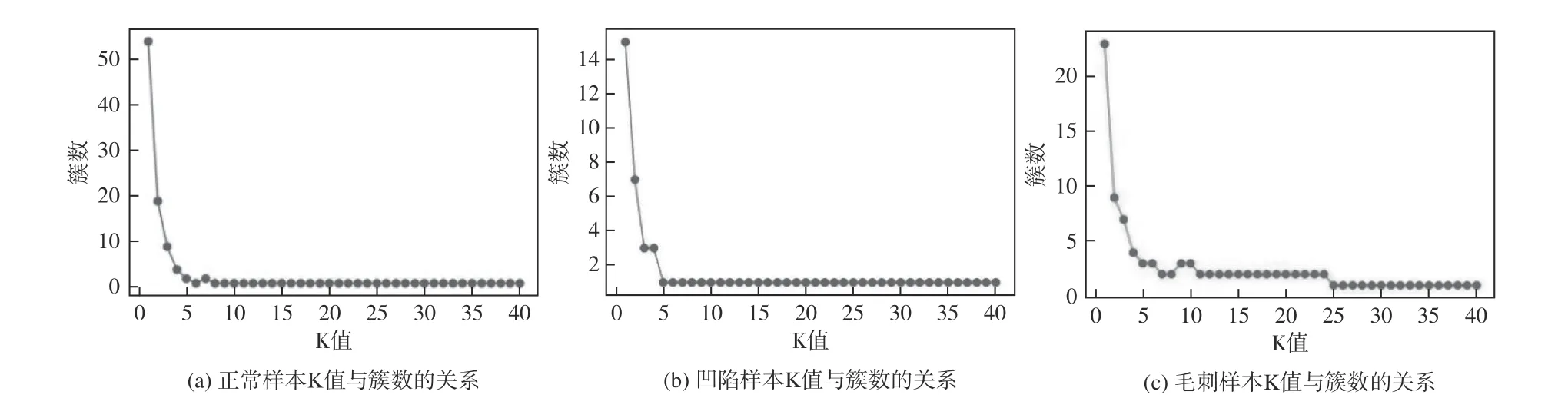
图 6 簇数-K 值的关系曲线Fig. 6 Relation curves of cluster number-K value
3 缺陷检测方法的流程
本文将灰度共生矩阵与聚类分析相结合,利用灰度共生矩阵提取刹车片表面纹理特征构造特征数据集,再用密度聚类方法分析数据集中的关联,缺陷检测流程图如图7 所示。
缺陷检测方法的具体步骤如下:
1) 通过工业相机、镜头、光源、支架搭建图像采集平台,采集刹车片摩擦块的正面图像,图像像素为2 592×1 944。利用双边滤波进行图像预处理,用Otsu 法、形态学等操作对图像进行分割,提取各个摩擦面图像,背景及钢背部分的灰度值均被置为0,从而去除背景及钢背对检测结果造成的干扰。
2) 将提取出的各块摩擦面图像分别切分成16×16 像素尺寸的小窗口,为每一个小窗口构建灰度共生矩阵,其方向为0°,步长为3,灰度级为16,然后计算角二阶矩、均值和、逆差矩、对比度、方差、相关性这6 个特征值作为六维特征向量,所有小窗口的特征向量即构成了用于聚类分析的数据集。
3) 对数据集进行去零点处理,同时利用PCA 算法降维,将六维数据降至二维数据,去除冗余数据的同时便于进行数据的可视化,然后利用自适应DBSCAN 算法对处理后的数据进行聚类分析。
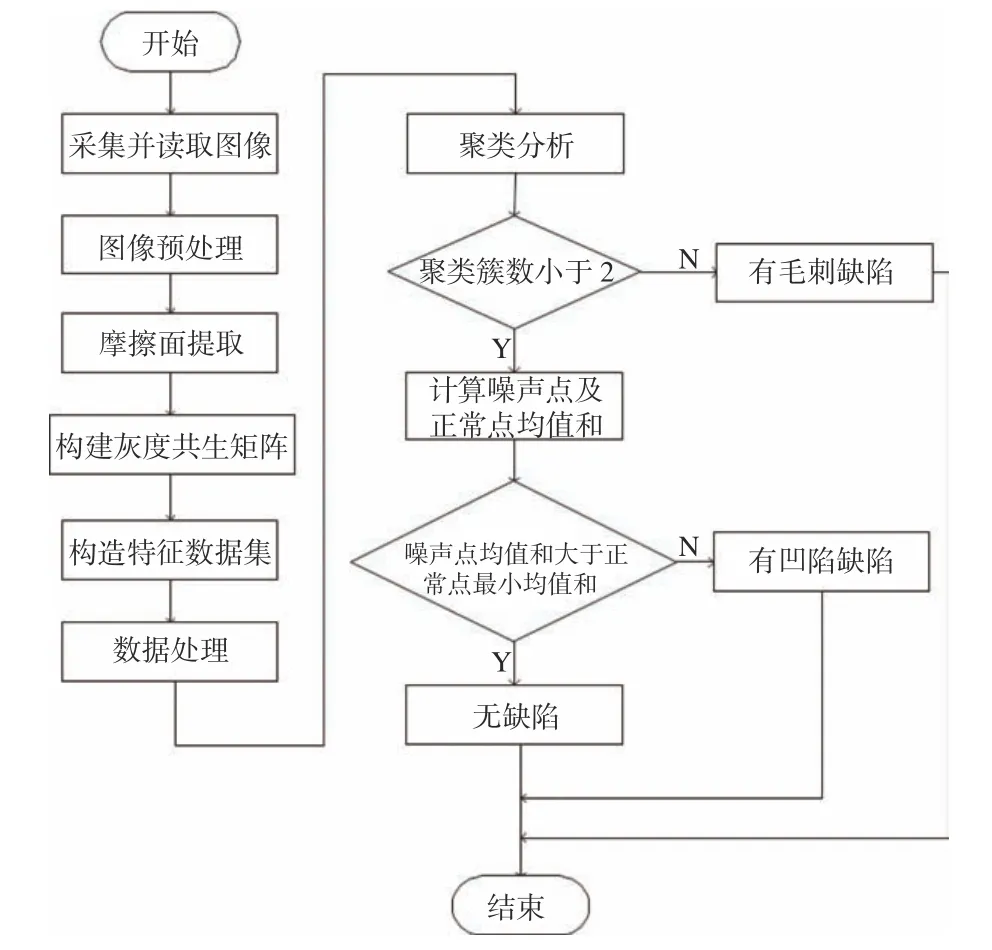
图 7 缺陷检测方法流程图Fig. 7 Flow chart of defects detection method
4) 在聚类过程中,若出现2 个及以上最佳聚类簇数的稳定区间,则立即判断该样本为含有毛刺缺陷样本,否则需要做进一步的判断是否存在凹陷缺陷,通过计算少量噪声点对应图像的均值和,将其与正常聚类的数据点对应图像的均值和相比较,若噪声点中存在均值和低于正常数据的点,该点即为凹陷部位而产生的异常点,可将该异常点数据对应的滑动小窗口在摩擦面图像上框出,显示凹陷缺陷的部位。
4 实验结果与分析
本实验使用的计算机硬件配置为Intel Core I5-7200U 四核2.7 GHz CPU 处理器,8 G 内存,开发环境为Window10 操作系统,开发软件为Spyder,采用Python 语言编程实现。
采集两种不同缺陷的刹车片的正面图像如图8所示,其中图8(a)为具有凹陷缺陷的刹车片样本,其最右边一块摩擦面上存在小部分的凹陷缺陷;图8(b)为具有毛刺缺陷的刹车片样本,其左右两块摩擦面的最外围均比较毛糙,即为毛刺缺陷,缺陷部位均由黑色曲线标记出来。图像预处理后,提取各个摩擦面的图像如图9 所示,图9(a)、9(b)、9(c)分别为凹陷样本分割出的3 块摩擦面,图9(d)、9(e)分别为毛刺样本分割出的两块摩擦面,可见,除摩擦面正常保留下来外,背景及钢背的灰度值均被置为零。

图 8 两种不同缺陷的刹车片表面图像Fig. 8 Brake pad surface image with two different defects

图 9 提取出的摩擦面图像Fig. 9 Extracted friction surface image
经密度聚类后,凹陷样本及毛刺样本特征数据的聚类结果可视化如图10 所示,图中圆形点为正常聚类的数据,叉形点为未被聚类的数据,即为噪声点。图10(a)、10(b)、10(c)分别为凹陷样本3 块摩擦面对应的数据聚类结果,可见聚类簇数只有一类,为正常部位产生的数据,凹陷部位产生的数据被检测为噪声点;图10(d)、10(e)为毛刺样本两块摩擦面对应的数据聚类结果。最佳聚类簇数有两类(分别为正常部位与毛刺部位产生的数据),统计a、b、c 面中正常数据点的最小均值和以及噪声点的均值和,结果如表3 所示。从表3 中可见只有摩擦面c 中出现了均值和低于正常窗口的噪声点,该噪声点即为异常点,从而判定摩擦面c 上存在缺陷部分。将该异常点对应的小窗口在摩擦面图像中框出,如图11所示,框出的部位正好为凹陷缺陷部位。从以上分析结果可以得出:根据缺陷检测流程,凹陷及毛刺缺陷均可被检测出。
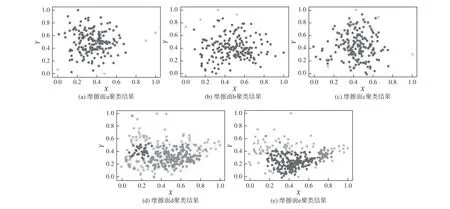
图 10 特征数据聚类结果可视化Fig. 10 Clustering results visualization of feature data
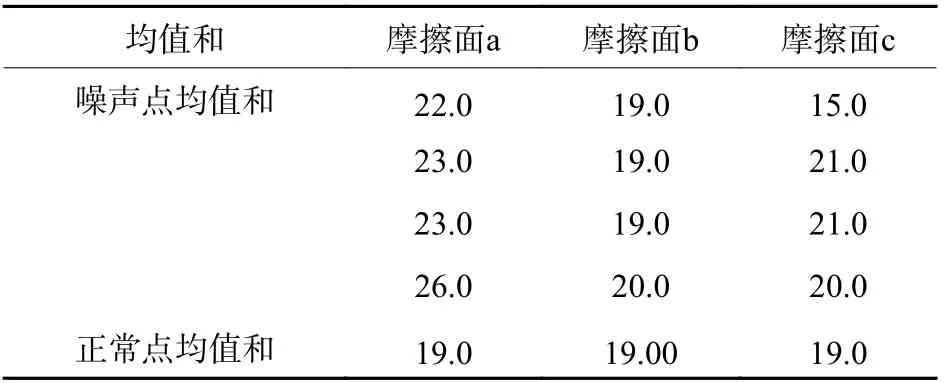
表 3 凹陷样本3 块摩擦面上噪声点对应的均值和Table 3 Corresponding mean value sum of noise points on three friction surfaces of concave sample

图 11 凹陷样本上框出的异常点Fig. 11 Anomalous points on concave sample
针对本文提出的方法,统计误检率和漏检率来衡量自动检测的效果,其中误检率为在正常样本被误判为缺陷样本的数量与全部正常样本数量的比值,漏检率为缺陷样本中被判断为正常样本的数量与所有缺陷样本的比值。通过试验,取58 块各个不同型号的刹车片,一共提取出120 块摩擦面,其中正常的摩擦面70 块,缺陷摩擦面50 块,根据实验统计结果,误检率为8%,漏检率为6%。
5 结论
通过目前的研究发现,本文提出的结合灰度共生矩阵及聚类分析的刹车片表面缺陷图像检测方法能够根据刹车片摩擦面自身的纹理情况提取特征,并根据特征数据集聚类分析的结果自动判断出是否存在缺陷部位,该方法不受刹车片型号及复杂表面纹理的限制,能够适用于大多数型号的刹车片,不需要提前制作模板,避免了繁琐的模板制作过程,节省了时间与成本。在实际工业生产的情况下,漏检一般比误检造成的结果更严重,因而需要尽可能降低漏检率。针对目前仍然存在一定的漏检率,下一步准备进一步提高摩擦面的提取效果,尽可能地去除采集到的刹车片图像中钢背及背景的干扰、保持摩擦面边缘的完整性,从而进一步降低一定的漏检率。

